高階耦合相振子系統(tǒng)的同步動力學(xué)*
蔡宗楷 徐燦? 鄭志剛?
1) (華僑大學(xué)信息科學(xué)與工程學(xué)院,廈門 361021)
2) (華僑大學(xué)系統(tǒng)科學(xué)研究所,廈門 361021)
由大量耦合相振子組成的Kuramoto 模型是研究各種自持續(xù)振蕩系統(tǒng)同步相變和集體動力學(xué)的重要模型.近些年,高階耦合Kuramoto 模型引起了廣泛的研究興趣,尤其高階耦合結(jié)構(gòu)在模擬編碼和信息存儲的動力學(xué)方面起到重要作用.為了研究高階耦合的影響,本文通過考慮頻率與耦合之間的關(guān)聯(lián)對高階耦合的Kuramoto 模型進(jìn)行了推廣,所得到的模型出現(xiàn)了一些新穎的動力學(xué)現(xiàn)象,包括多集團(tuán)態(tài)(多團(tuán)簇態(tài))、雙穩(wěn)態(tài)、爆炸性同步以及振蕩態(tài).對無序態(tài)的線性穩(wěn)定分析得到表征系統(tǒng)由無序向同步轉(zhuǎn)變的臨界耦合強(qiáng)度,利用自洽方法分析得到系統(tǒng)的多團(tuán)簇態(tài),并進(jìn)一步在等效低維子空間中對多團(tuán)簇態(tài)進(jìn)行線性穩(wěn)定性分析得到穩(wěn)定的多團(tuán)簇態(tài)解以及去同步相變點.對理論分析結(jié)果的討論總結(jié)了系統(tǒng)由遲滯到振蕩態(tài)的轉(zhuǎn)變.此外,本文強(qiáng)調(diào)結(jié)合表征系統(tǒng)不對稱性的Kuramoto 序參量和表征系統(tǒng)多團(tuán)簇態(tài)的Daido 序參量可以對系統(tǒng)宏觀動力學(xué)給出完整的描述.通過本文的研究可以進(jìn)一步加深對高階耦合相振子系統(tǒng)中耦合異質(zhì)性以及爆炸性同步的理解.
1 引言
同步涌現(xiàn)是耦合非線性系統(tǒng)中的一個顯著現(xiàn)象,對這種自組織行為的研究涵蓋了物理學(xué)、工程學(xué)、生物學(xué)以及社會系統(tǒng)等多個學(xué)科領(lǐng)域.典型的例子包括超導(dǎo)中的耦合約瑟夫森結(jié)、電力網(wǎng)絡(luò)、心臟起搏器、大腦中的神經(jīng)元放電以及觀眾現(xiàn)場掌聲的形成等[1?4].探索通往同步的道路并揭示這種集體行為背后的內(nèi)在機(jī)制具有重要的現(xiàn)實意義,也為理解復(fù)雜系統(tǒng)宏觀動力學(xué)提供理論依據(jù)[5?7].
在研究同步問題的諸多模型中,一個典型的范例是著名的Kuramoto 模型[8],該模型于1975 年被正式提出.Kuramoto 模型由具有隨機(jī)固有自然頻率的相振子系統(tǒng)組成,并且振子間通過相差的正弦函數(shù)進(jìn)行全局耦合.Kuramoto 模型由弱耦合極限環(huán)振子通過快慢時間尺度分離絕熱地消去系統(tǒng)的振幅效應(yīng)而得到,在這一框架下,系統(tǒng)從無序到有序的同步轉(zhuǎn)變可以被看作是一種典型的非平衡相變.經(jīng)典的Kuramoto 模型指出系統(tǒng)從無序態(tài)到同步態(tài)的轉(zhuǎn)變呈現(xiàn)出一系列連續(xù)相變,相應(yīng)地,刻畫系統(tǒng)同步程度的序參量經(jīng)歷了一個從零到非零的超臨界分岔,這一同步轉(zhuǎn)變特性與統(tǒng)計力學(xué)中的二級相變十分類似[9?11].
最初的Kuramoto 模型及其各種形式的推廣通常局限于每個振子之間的單次諧波相互作用,即耦合函數(shù)只包含每一對相互作用振子之間相差的一次簡諧函數(shù).為了更好地描述大量現(xiàn)實系統(tǒng)中集體節(jié)律的形成,近年來研究者對高階耦合相振子系統(tǒng)開展了廣泛的研究[12?17],即系統(tǒng)的耦合函數(shù)包含了相差的二階乃至更高階簡諧項,這類高階耦合相振子模型被統(tǒng)稱為Kuramoto–Daido 模型,這類模型與現(xiàn)實中的許多物理系統(tǒng)密切相關(guān)[18?22].最近研究表明,作為Kuramoto 耦合相振子模型的一種重要推廣,當(dāng)耦合函數(shù)引入高階結(jié)構(gòu)時,相較于單純的一階耦合,系統(tǒng)會產(chǎn)生一系列新穎的動力學(xué)現(xiàn)象[23?29],例如多集團(tuán)態(tài)、廣泛多穩(wěn)態(tài)、一系列爆炸性去同步轉(zhuǎn)變等[30?35].此外,全局高階耦合相振子系統(tǒng)中涌現(xiàn)出一系列非平庸動力學(xué)特性可以用來有效地模擬編碼和數(shù)據(jù)存儲,也為揭示人腦中結(jié)構(gòu)與功能的關(guān)聯(lián)提供了重要的理論啟示.以往對高階耦合相振子的研究集中在振子間為均勻的耦合方式,而現(xiàn)實中個體間的相互作用往往是異質(zhì)性且非對稱的,例如社交中人與人之間的交流受到個體性格差異的影響、大腦中神經(jīng)元連接的不對稱性以及電力網(wǎng)絡(luò)中節(jié)點間耦合存在差異等.由此本文主要考慮異質(zhì)性且非對稱的耦合,耦合異質(zhì)性的引入也使得系統(tǒng)的宏觀動力學(xué)行為和發(fā)生的相變過程完全不同(相比于均勻耦合系統(tǒng)中出現(xiàn)的連續(xù)的二級相變),除了多集團(tuán)態(tài)、廣泛多穩(wěn)態(tài),系統(tǒng)還將出現(xiàn)由表征系統(tǒng)一級相變的遲滯現(xiàn)象向振蕩態(tài)的轉(zhuǎn)變,此外系統(tǒng)中表現(xiàn)出的爆炸式同步相變與現(xiàn)實中一些突發(fā)性現(xiàn)象具有高度相似性,對爆炸式同步的研究具有重要的現(xiàn)實意義.
本文研究了具有高階耦合結(jié)構(gòu)的全局耦合相振子系統(tǒng)中出現(xiàn)的新奇同步相變.通過建立自然頻率與耦合之間的聯(lián)系進(jìn)行研究,結(jié)果表明這種推廣模型是可以被精確求解的.特別地,文章揭示一階和二階序參量的結(jié)合運(yùn)用可以很好地描述系統(tǒng)的動力學(xué).尤其是當(dāng)考慮自然頻率服從雙峰分布時,系統(tǒng)的同步相變形式依賴于頻率分布參數(shù).具體而言,當(dāng)頻率分布的中心頻率較小時,用來表征系統(tǒng)出現(xiàn)多團(tuán)簇態(tài)的Daido 序參量表現(xiàn)出爆炸性去同步和同步的不可逆一級相變,而刻畫不對稱程度的Kuramoto 序參量則表現(xiàn)出依賴于不對稱度參數(shù)的爆炸性同步和去同步(abrupt synchronization and desynchronization transition,ASDT).當(dāng) 頻率分布的中心頻率增大時,表征系統(tǒng)一級相變的遲滯現(xiàn)象隨之消失,宏觀序參量表現(xiàn)為不連續(xù)同步和去同步振蕩態(tài)(oscillatory state,Os).本文從無序態(tài)線性穩(wěn)定性分析出發(fā),解析地得到表征無序態(tài)失穩(wěn)的臨界耦合強(qiáng)度.緊接著,通過自洽方法分析得到系統(tǒng)的多團(tuán)簇態(tài),并在等效低維子空間中對多團(tuán)簇態(tài)進(jìn)行線性穩(wěn)定性分析,得到多團(tuán)簇態(tài)的穩(wěn)定解.結(jié)合無序態(tài)穩(wěn)定性分析和多團(tuán)簇態(tài)分析的結(jié)果揭示了系統(tǒng)由ASDT 到Os 的轉(zhuǎn)變機(jī)制.
本文內(nèi)容安排如下:第2 節(jié)引入高階耦合的動力學(xué)模型,并展示了該動力學(xué)模型的數(shù)值模擬結(jié)果;第3 節(jié)進(jìn)行理論分析,包括通過無序態(tài)的穩(wěn)定分析得到依賴于頻率分布參數(shù)的臨界耦合強(qiáng)度,利用自洽分析得到了系統(tǒng)的多團(tuán)簇態(tài)解,以及對多團(tuán)簇態(tài)的穩(wěn)定性分析得到穩(wěn)定的多團(tuán)簇態(tài)解,并結(jié)合各分析結(jié)果討論系統(tǒng)相變機(jī)制的轉(zhuǎn)變;最后,在第4 節(jié)對全文內(nèi)容進(jìn)行概括總結(jié),并對高階耦合的研究進(jìn)行展望.
2 理論模型及數(shù)值模擬
2.1 理論模型
首先,考慮將經(jīng)典Kuramoto 模型推廣到一般的高階耦合相振子模型,其動力學(xué)演化方程如下:
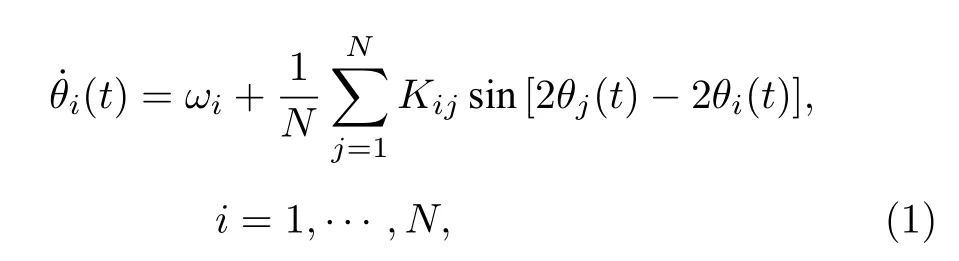
式中,‘‘·”表示對時間的導(dǎo)數(shù),θi(t) 表示第 i 個振子在 t 時刻的相位,ωi是振子 i 的固有自然頻率,一般取自一個給定的概率分布函數(shù) g(ω).Kij代表第i個振子和第 j 個振子間的耦合強(qiáng)度,并且耦合強(qiáng)度大于 0 表示振子間的相互吸引.與振子間的相互作用為均勻耦合的經(jīng)典Kuramoto 模型相比,該模型中的耦合強(qiáng)度是異質(zhì)性且非對稱的,即 KijKji,由此更能反映實際耦合的非對稱的本質(zhì)[36,37],這也與大腦中的神經(jīng)元連接的不對稱性一致.
為了突出耦合的異質(zhì)性,這里考慮一種特殊的情形,即 Kij=K|wi|,且 K >0[38?47],這種耦合稱為內(nèi)耦合,即在耦合系統(tǒng)中通過建立耦合強(qiáng)度與振子本身固有頻率的關(guān)聯(lián)而賦予振子間耦合的異質(zhì)性,在這樣的框架下,耦合的異質(zhì)性源自振子本身的固有特性.頻率權(quán)重模型通常被用來揭示耦合相振子系統(tǒng)通往同步過程中發(fā)生的一級相變[48?53],但是這些研究工作僅僅考慮相差的一次簡諧函數(shù).本文主要研究高階耦合相振子系統(tǒng)在自然頻率的分布為雙峰對稱情形下的動力學(xué)特性.
為了描述系統(tǒng)的宏觀動力學(xué)特性,引入兩個復(fù)序 參量,定義為
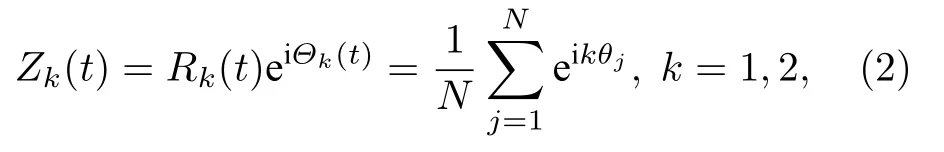
其中,Zk(t) 是宏觀變量,對應(yīng)于復(fù)平面單位圓上N個振子 {eikθ} 的質(zhì)心.Rk(t) 和 Θk(t) 分別是復(fù)序參量 Zk(t) 的幅值和幅角.Z1(t) 是Kuramoto 序參量,而 Z2(t) 則被稱作Daido 序參量.從下文將會發(fā)現(xiàn),這兩個序參量的組合可以很好地描述方程(1)的宏觀動力學(xué).這組序參量可以被解釋為由振子群產(chǎn)生的集體節(jié)律,特別地,Z2(t)可以衡量振子間的同步程度以及集團(tuán)態(tài)的形成,而 Z1(t) 則反映系統(tǒng)的不對稱度,尤其當(dāng)所有振子同步到兩個不同的團(tuán)簇上時.顯然,當(dāng)系統(tǒng)在單位圓上的不同位置出現(xiàn)多個同步團(tuán)簇時,Z2(t) 可以更好地刻畫系統(tǒng)的同步程度,而 Z1(t) 則表示團(tuán)簇間的大小差異,即兩個團(tuán)簇的不對稱程度.具體而言,R1=0 表明兩個同步團(tuán)簇完全對稱,幅角相差 π,而當(dāng) R1=1 時,意味著整個系統(tǒng)表現(xiàn)為一個巨大的振子團(tuán)簇,說明了系統(tǒng)達(dá)到完全同步.
對上述的頻率權(quán)重內(nèi)耦合相振子,其動力學(xué)方程 可寫成
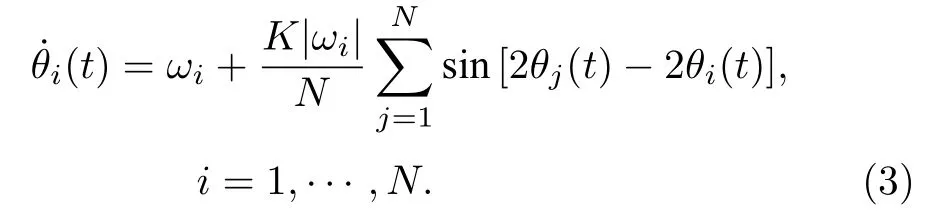
由(2)式定義的序參量方程可以將方程(3)改寫成平 均場的形式:
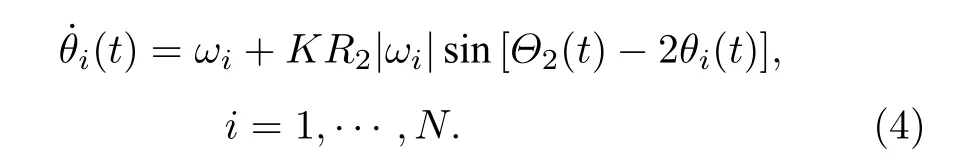
很顯然,寫成平均場的形式,每一個振子的演化僅僅與兩個宏觀參量 R2和Θ2耦合,而與其他所有振子似乎解耦了,且對每一個振子而言,與平均場 的有效作用強(qiáng)度為 KR2|ωi|.
2.2 數(shù)值模擬結(jié)果
接下來,通過展示方程(3)的數(shù)值模擬結(jié)果來直觀地了解該系統(tǒng)所表現(xiàn)出的新穎的動力學(xué)現(xiàn)象.以 N=50000 個振子數(shù),利用四階Runge-Kutta方法對方程(3)進(jìn)行數(shù)值模擬,自然頻率分別服從雙峰洛倫茲分布
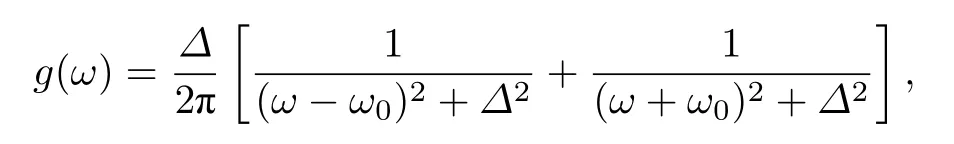
和均勻分布

為了方便討論,對于雙峰洛倫茲分布,固定Δ=0.1觀察不同 ω0情形下系統(tǒng)隨耦合強(qiáng)度的改變(增加或減小)所表現(xiàn)出的同步相變過程,而對于均勻分布直接固定 γ=1 觀察其同步相變過程,并且在持續(xù)增大耦合強(qiáng)度 K 時選取任意的相位初始條件θi(0),而在持續(xù)減小耦合強(qiáng)度 K 的過程中,以不同概率 α 和 1?α 分別選取相位初始條件為θi(0)=0和 θi(0)=π.
圖1 給出了自然頻率服從雙峰洛倫茲情形下序參量 R2和 R1對應(yīng)不同初始條件和頻率分布參數(shù)下隨耦合強(qiáng)度 K 的相變圖.其中,雙峰洛倫茲分布的半寬 Δ 固定為 0.10,中心頻率 ω0取值分別為0.08(圖1(a)),0.12 (圖1(b)),0.30 (圖1(c)),和0.40(圖1(d)).α 分別取 1.00 (粉),0.90 (青),0.80(藍(lán)),0.70(綠),0.60 (紅).圖1 中的正三角形表示序參量隨耦合強(qiáng)度增大方向的點,而倒三角形表示序參量隨耦合強(qiáng)度減小方向的點.當(dāng) ω0相對較小時,從圖1(a1)和圖1(b1)可以看出Daido 序參量R2隨耦合強(qiáng)度 K 的變化經(jīng)歷了一級相變,即當(dāng) K從小往大增加時,在臨界耦合 Kf處二階序參量 R2發(fā)生由無序態(tài)(R2=0)到同步態(tài)(R2>0)的不連續(xù)跳變.而當(dāng)耦合強(qiáng)度 K 由大減小的過程中,R2從同步態(tài)(R2≈0.71)到無序態(tài)(R2≈0)的去同步轉(zhuǎn)變也是以不連續(xù)跳變的形式,并且去同步臨界耦合強(qiáng)度為 Kb≈2

圖1 序參量R2 和 R1隨耦合強(qiáng)度K的相變圖.g(ω)為雙峰洛倫茲分布,且Δ=0.10,ω0分別取(a)0.08,(b)0.12,(c) 0.30,(d) 0.40.其中正三角形△表示耦合強(qiáng)度K增大的方向,倒三角形▽表示耦合強(qiáng)度K 減小的方向.(a2)?(d2)中R1的相變曲線自上往下 α 分別取 1.00 (粉,方形),0.90 (青,圓形),0.80 (藍(lán),菱形),0.70 (綠,左三角),0.60 (紅,右三角)Fig.1.Phase transition diagram of order parameters R2 and R1 with the coupling strength K.g(ω) is bimodal Lorentz distribution with Δ=0.10,and ω0=0.08 (a),0.12 (b),0.30 (c),0.40 (d),respectively.The regular triangle △ indicates the direction of the increase of coupling strength K and the inverted triangle ▽ indicates the direction of the decrease of coupling strength K.In(a2)?(d2),phase transition of R1 with α=1.00(pink,square),0.90 (cyan,circle),0.80(blue,diamond),0.70(green,left triangle)and 0.60 (red,right triangle) from top to bottom,respectively.
當(dāng) ω0較大時(圖1(c)和圖1(d)),宏觀序參量R2和 R1的動力學(xué)現(xiàn)象與之前的圖1(a)和圖1(b)又截然不同.首先,隨著耦合強(qiáng)度的增大或減小時,序參量 R2并不存在遲滯現(xiàn)象,并且在減小和增大K的過程中 R2的相變是對稱的.具體而言,系統(tǒng)的無序態(tài) R2=0 在 Kf<2 處失穩(wěn),對于同步態(tài)而言,R2在Kb≈2 處發(fā)生不連續(xù)跳變,在區(qū)間Kf 從圖2 可以清晰地看到序參量 R2和 R1隨時間是周期振蕩的,并且振蕩的最低點都是 0,于是,在此將系統(tǒng)的宏觀序參量 R2和 R1隨時間 t 表現(xiàn)出周期振蕩的行為稱為振蕩態(tài).同樣,對于 R1而言,其隨時間振蕩的幅度依賴于不對稱度參數(shù) α.為了進(jìn)一步考察自然頻率分布對系統(tǒng)宏觀動力學(xué)的影響,圖3 展示了自然頻率服從半寬為 1 的均勻分布,其情形與圖1(c)、圖1(d)和圖2 類似.系統(tǒng)無遲滯存在,宏觀序參量R2和 R1在相變過程中呈現(xiàn)出振蕩態(tài),同時,R1的同步態(tài)和振蕩態(tài)也依賴于不對稱度參 數(shù) α. 圖3 g(ω) 為均勻分布,γ=1.0 (a),(b)序參量 R2 和 R1 隨耦合強(qiáng)度 K 的相變圖.其中相變曲線自上往下 α 分別取 1.00 (粉,方形),0.90 (青,圓形),0.80 (藍(lán),菱形),0.70 (綠,左三角),0.60 (紅,右三角).(c),(d)耦合強(qiáng)度 K=1.90 時序參量 R2 和 R1 隨時間t的演化.圖中 R1 曲線自上往下 α 分別取 1.0 (粉,實線),0.9 (青,劃線),0.8 (藍(lán),點線),0.7 (綠,點劃線),0.6 (紅,雙點劃線)Fig.3.g(ω) is uniform distribution with γ=1.0 (a),(b) Phase transition diagram of order parameters R2 and R1 with the coupling strength K.Phase transition of R1 with α=1.00 (pink,square),0.90 (cyan,circle),0.80 (blue,diamond),0.70 (green,left triangle) and 0.60 (red,right triangle) from top to bottom,respectively.(c),(d) Evolution of the order parameters R2 and R1 with time t at coupling strength K=1.90.The curve of R1 with α=1.00 (pink,solid line),0.90 (cyan,dash line),0.80 (blue,dot line),0.70 (green,dash dot line),0.60 (red,dash dots line) from top to bottom,respectively. 考慮熱力學(xué)極限情況下(N →∞),系統(tǒng)的狀態(tài)可以用概率密度分布函數(shù) ρ(θ,ω,t) 來描述.其中,ρ(θ,ω,t)dθdω表示在 t 時刻介于區(qū)間ω ∈(ω,ω+dω)和 θ ∈(θ,θ+dθ)內(nèi)振子的比例.此外,ρ(θ,ω,t) 是關(guān) 于相位 θ 周期為 2π 的函數(shù),并且滿足歸一化條件 由于在 N趨于無窮時,系統(tǒng)的振子數(shù)守恒,故分布函 數(shù) ρ(θ,ω,t)滿足以下連續(xù)性方程: 其中,速度 v(θ,ω,t) 為 相應(yīng)地,由(2)式定義的宏觀序參量 Zk在連續(xù)極限的情況下寫成積分的形式為 接下來將通過系統(tǒng)的無序態(tài)線性穩(wěn)定性分析得到無序態(tài)失穩(wěn)點,即系統(tǒng)隨耦合強(qiáng)度 K 增加由無序向同步轉(zhuǎn)變的臨界耦合強(qiáng)度 Kf.ρ0(θ,ω,t)=1/2π表示系統(tǒng)的無序態(tài),對應(yīng)于連續(xù)性方程(6)的平庸解.相應(yīng)地,序參量 Zk=0,所有振子以自然頻率繞單位圓運(yùn)動. 對 ρ(θ,ω,t) 在平庸解 ρ0附近考慮一個小的擾動 其中,ε 是擾動幅值,且 0<ε ?1,ν(θ,ω,t) 是關(guān)于相位 θ 周期為2π 的擾動函數(shù).由(5)式的歸一化條件可以得到 ν(θ,ω,t) 對 θ 的均值為 0,即 由此,序參量在擾動的作用下改寫成關(guān)于擾動函數(shù)的形式 相應(yīng)地,速度 v(θ,ω,t) 可寫成如下形式: 由于 ν(θ,ω,t) 是關(guān)于 θ 周期為 2π 的函數(shù),可以將ν(θ,ω,t)對θ 進(jìn)行傅里葉級數(shù)展開: 其中,νn(ω,t) 為傅里葉展開系數(shù),由于 ν(θ,ω,t) 是實函數(shù),故而 ν0(ω,t)=0 且 νn(ω,t)=將(14)式代入(11)式得到關(guān)于Daido 序參量的簡潔形式: 從(15)式右邊可以發(fā)現(xiàn),僅 ν(θ,ω,t) 傅里葉級數(shù)展開的二次簡諧項對非平庸線性化振幅方程有作用,這與方程(3)定義的高階耦合有關(guān).將(14)式代入方程(13)可以直觀地得到這一結(jié)論,即 對方程(16)右邊定義一個線性算符,即 很顯然,(17)式右邊第一項為乘積算子,其相應(yīng)的本征值為 λ=?2iω,而右邊第二項可以看作是擾動算子作用在第一項上.文獻(xiàn)[54,55]指出線性算子的本征譜在微擾作用下保持不變,且文獻(xiàn)[56]表明 L 的連續(xù)譜就是乘積算子的本征值,即σc(L)={λ=?2iω,ω ∈support(g)}.與傳統(tǒng)的Kuramoto 模型及其推廣模型一樣,L 的連續(xù)譜是純虛的,并不會誘導(dǎo)高階耦合相振子系統(tǒng)的無序態(tài)線性失穩(wěn). 緊接著,分析 L 的離散譜.對于 λ ∈Cσc(L),令 結(jié)合(17)式和(18)式,得 式中 λ 的實部決定了無序態(tài)的穩(wěn)定性.對于(20)式,很容易驗證如果 λ 存在,那么其實部一定非負(fù),因此,表征系統(tǒng)無序態(tài)失穩(wěn)的臨界耦合強(qiáng)度 Kf通過取極限 Re(λ)→0+和 Im(λ)→Ωc可求得.令λ=x+iy,那么本征方程(20)在極限條件下可分別寫成實部和虛部兩個等式,即 其中,P.V.表示對 ω 沿實軸的主值積分.最終可以確定臨界耦合強(qiáng)度 Kf的一般形式 其中,臨界平均場頻率 Ωc由平衡方程(22)確定.如,對于單位半寬的單峰洛倫茲分布,其 Ωc=±2,相應(yīng)地,Kf=4.對于ω∈[?1,1] 的均勻分布,其而本文主要考慮的雙峰洛倫茲分布,其臨界頻率為 相應(yīng)地,臨界耦合強(qiáng)度為 固定 Δ=0.1,如果 ω0=0.08,那么Kf≈3.12(圖1(a1)),同樣地,ω0=0.12,Kf≈2.56 (圖1(b1)),ω0=0.30,Kf≈1.26 (圖1(c1)),ω0=0.40,Kf≈0.97(圖1(d1)).通過改變不同的中心頻率 ω0,可得到不同的臨界耦合強(qiáng)度Kf,并且表征無序態(tài)失穩(wěn)的臨界耦合強(qiáng)度 Kf與表征同步態(tài)去同步的臨界耦合強(qiáng)度的大小關(guān)系,可產(chǎn)生完全不同的宏觀相變過程(圖1(a1)、圖1(b1)與圖2(c1)、圖1(d1))與微觀動力學(xué)現(xiàn)象. 由以上的無序態(tài)線性穩(wěn)定性分析可知,對于K 為了更好地理解系統(tǒng)動力學(xué)分岔以及同步相變機(jī)制,接下來利用自洽方法分析系統(tǒng)長時間演化的宏觀動力學(xué)特性.自洽方法最核心的思想就是假定系統(tǒng)在長時間的演化之后處于定態(tài),即 Rk(t) 為隨時間不變的定值,且 Θk(t) 均勻旋轉(zhuǎn).由于方程(3)滿足旋轉(zhuǎn)不變性和反演對稱性,在旋轉(zhuǎn)框架下選取適當(dāng)?shù)某跏紬l件可以令 Θ(t)=0,故而 Zk=Rk.此時平均場方程為 根據(jù) KR2的幅值大小,系統(tǒng)會表現(xiàn)出兩種不同的宏觀動力學(xué)行為.當(dāng) KR2>1 時,所有振子都會被鎖住,與自然頻率大小無關(guān),并且鎖相相位滿足 按照三角函數(shù)恒等式變換,可求得 其中,δ(·) 表示Dirac 函數(shù),參數(shù) α 是反映兩個團(tuán)簇間的不對度.當(dāng) KR2<1時,所有振子處于漂移的狀態(tài),并在單位圓上非均勻地運(yùn)動,此時的相位分布為 相應(yīng)地,序參量也分為兩種不同的情形進(jìn)行討論,分別為 和 其中,〈·〉 表示所有振子取平均.在連續(xù)極限的情況下,按照(8)式關(guān)于序參量的定義以及系統(tǒng)的對稱性,可以計算得到關(guān)于二階序參量的一個簡潔形式: 由此可解得 對于實數(shù) K 和 R2,(36)式有解必須滿足 K ≥2.結(jié)合序參量 R1的定義和 R2的表達(dá)式,求得 R1關(guān)于耦合強(qiáng)度 K 和不對稱度參數(shù) α 的表達(dá)式為 由(37)式可以看出,序參量 R1是取決于不對稱度參數(shù) α 的廣泛多穩(wěn)態(tài),而由序參量 R2的表達(dá)式(36)式可知,R2只與耦合強(qiáng)度有關(guān),并不依賴于不對稱度參數(shù) α.對于足夠大的耦合強(qiáng)度 K,序參量 R2有兩支解,且其中一支是穩(wěn)定的,另一支是不穩(wěn)定的,下文將證明其中是穩(wěn)定的,是不穩(wěn)定的.在耦合強(qiáng)度 K 由大逐漸減小的過程中,序參量 R1和 R2的每一支解都會在相同的臨界耦合強(qiáng)度 Kb=2 處消失,表明系統(tǒng)在此處發(fā)生爆炸性去同步轉(zhuǎn)變,至于去同步之后系統(tǒng)會處于無序態(tài)還是振蕩態(tài)取決于振子自然頻率分布的中心頻率. 3.2 節(jié)基于自洽方程得到了多團(tuán)簇態(tài)的一般形式,但是其穩(wěn)定性特性仍然是模糊的,使得對系統(tǒng)集體動力學(xué)的理解不夠深刻.這一節(jié)將解決多集團(tuán)態(tài)的穩(wěn)定性問題,具體而言,就是對各個團(tuán)簇進(jìn)行線性穩(wěn)定性分析. 從(27)式可以看出,鎖相時所有振子被鎖在4 個團(tuán)簇,分別為換句話說,對于 N 維的的系統(tǒng)方程(3),最終演化到一個4維的子流形.在這樣的低維子空間中,系統(tǒng)的演化方程退化到一個相對簡潔的形式: 其中,ω >0為團(tuán)簇 θp的自然頻率.接著,引入相差φ=θp?θn,那么可以得到相差 φ 的演化方程 顯然,當(dāng) K >2 時,(40)式存在兩個不動點,即 對(40)式進(jìn)行線性穩(wěn)定性分析,可以很容易得到穩(wěn)定的條件為 cos(2φ)>0.并且,注意到 因此,穩(wěn)定條件 cos(2φ)>0 等價于 從3.3 節(jié)的多團(tuán)簇態(tài)的穩(wěn)定性分析可以得到,在耦合強(qiáng)度 K >Kb=2 時,多團(tuán)簇態(tài)的解存在且穩(wěn)定.又由3.1 節(jié)無序態(tài)的穩(wěn)定性分析得到,無序態(tài)的失穩(wěn)點 Kf的一般表達(dá)式((23)式),與自然頻率分布函數(shù)的中心頻率 ω0和半寬 Δ 有關(guān),若固定 Δ 為常數(shù)不變,那么表征無序態(tài)失穩(wěn)的臨界耦合強(qiáng)度 Kf將隨著 ω0增大而減小.當(dāng) ω0較小時,使得Kf>Kb,就會出現(xiàn)遲滯現(xiàn)象(圖2(a)和圖2(b)),具體而言,當(dāng)耦合強(qiáng)度從小往大增加時,無序態(tài)將在Kf>Kb=2處失穩(wěn),所有振子發(fā)生同步,且臨界點處的序參量>0,可由(36)式和(37)式及(43)式求得,分別為 序參量 RK在臨界點由 RK=0 直接向 RK>0 發(fā)生跳變,表現(xiàn)為不連續(xù)相變(一級相變),即爆炸式同步.同樣地,當(dāng)耦合強(qiáng)度由大往小減時,多團(tuán)簇態(tài)將在 Kb=2 處去同步,且 序參量由非 0 跳到0,表現(xiàn)為爆炸式去同步,值得注意,耦合強(qiáng)度在 Kb 綜上,本文探討了耦合強(qiáng)度與頻率關(guān)聯(lián)的高階耦合相振子的動力學(xué).由數(shù)值模擬與理論分析得出,在自然頻率服從雙峰分布的情形下,隨著自然頻率分布的中心頻率的增加,系統(tǒng)將由ASDT 向Os 轉(zhuǎn)變.具體而言,首先,利用無序態(tài)線性穩(wěn)定性分析得到了系統(tǒng)發(fā)生同步的臨界耦合強(qiáng)度,再通過自洽分析得到系統(tǒng)的多團(tuán)簇態(tài)及其一般表達(dá)式,并對多團(tuán)簇態(tài)進(jìn)行線性穩(wěn)定性分析得到其穩(wěn)定解.當(dāng)頻率分布的中心頻率較小時,系統(tǒng)由無序向同步轉(zhuǎn)變的臨界耦合強(qiáng)度大于多團(tuán)簇態(tài)的去同步點,將存在無序態(tài)與多團(tuán)簇態(tài)共存的雙穩(wěn)態(tài),此時系統(tǒng)表現(xiàn)為ASDT.當(dāng)增大自然頻率分布的中心頻率,系統(tǒng)無序態(tài)失穩(wěn)的臨界耦合強(qiáng)度小于多團(tuán)簇態(tài)的去同步點,此時,遲滯消失且在無序態(tài)失穩(wěn)點與多團(tuán)簇態(tài)去同步點之間存在非定態(tài)解,即Os.值得注意,本文指出二階序參量可以很好地描述系統(tǒng)多團(tuán)簇態(tài)的形成,而一階序參量則反映系統(tǒng)的不對稱性. 本文旨在考察高階耦合結(jié)構(gòu)對耦合相振子集體動力學(xué)的影響,但該模型在研究自然界中的同步現(xiàn)象以及社會中的復(fù)雜系統(tǒng)建模等相關(guān)具體應(yīng)用還有待進(jìn)一步研究.本文僅對全局耦合相振子系統(tǒng)所表現(xiàn)出的動力學(xué)現(xiàn)象給出理論基礎(chǔ),缺乏對現(xiàn)實因素的考量以及系統(tǒng)網(wǎng)絡(luò)結(jié)構(gòu)的討論,這些問題將有待進(jìn)一步得到分析解決.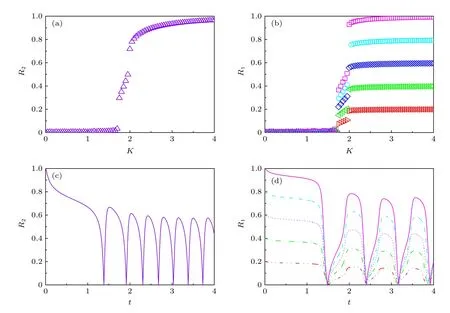
3 理論分析
3.1 無序態(tài)穩(wěn)定性分析

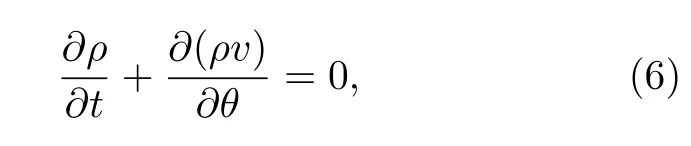
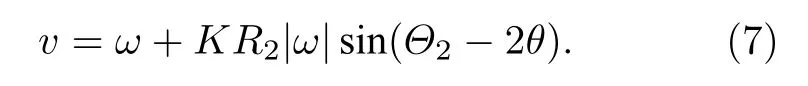
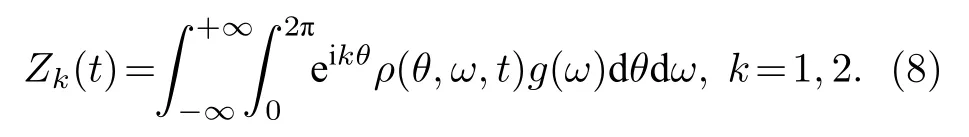
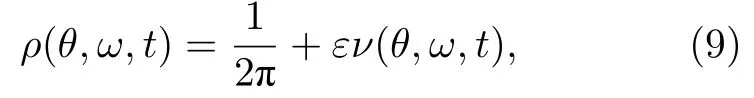
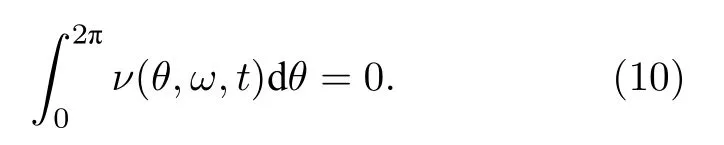
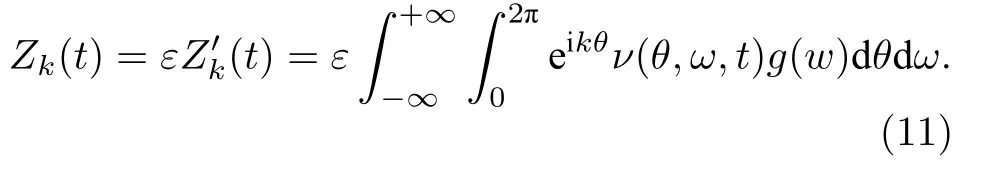
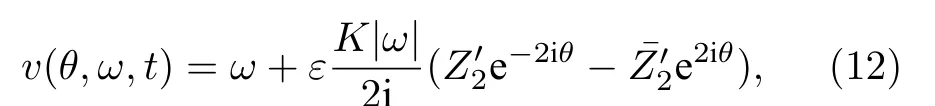
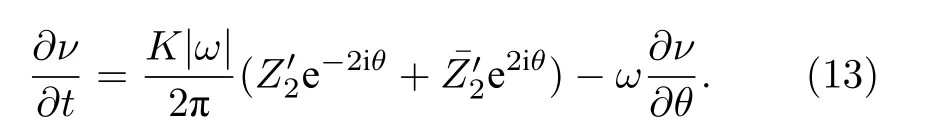
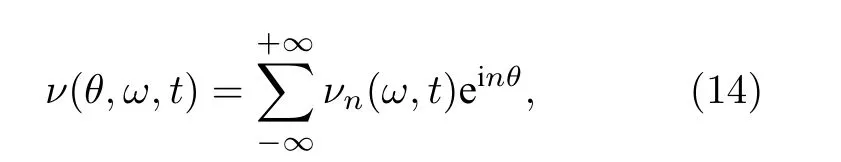

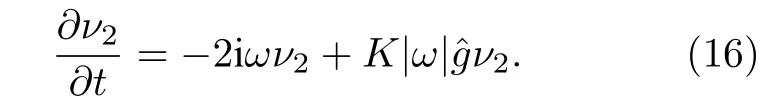
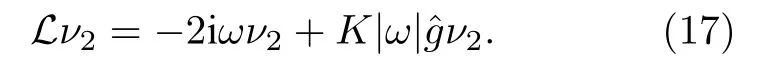


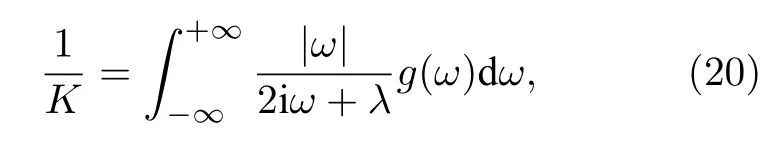
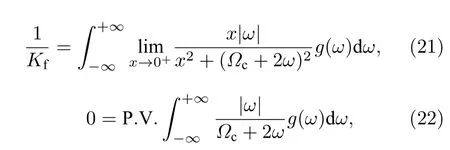
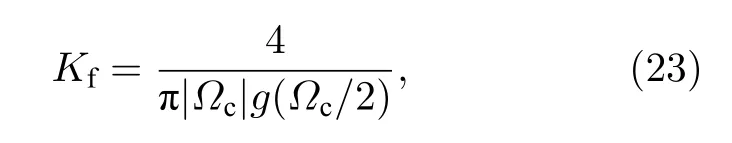
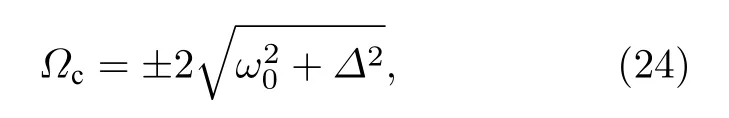

3.2 自洽方法



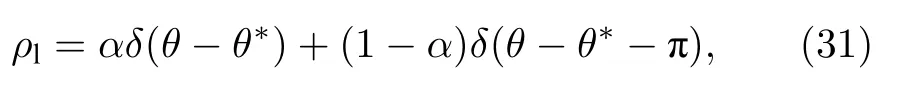



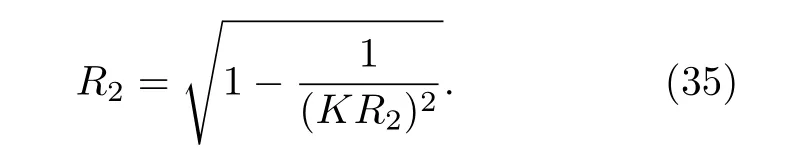
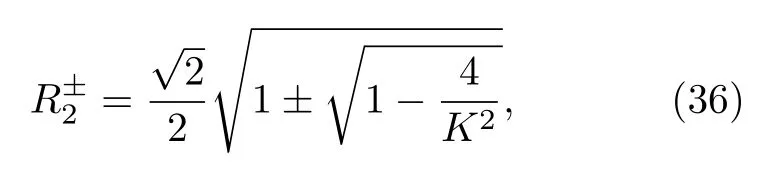
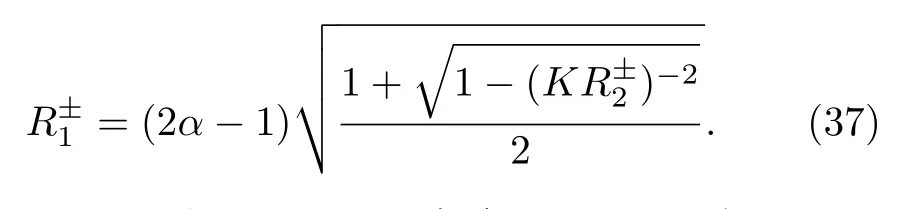
3.3 多團(tuán)簇態(tài)穩(wěn)定性分析
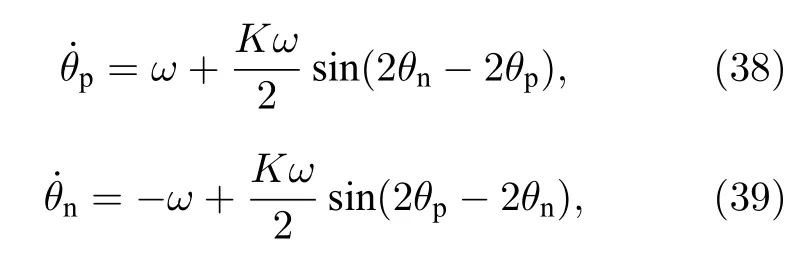
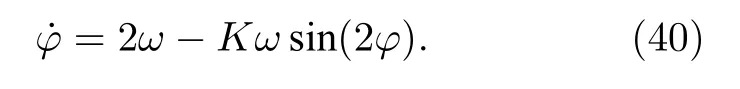

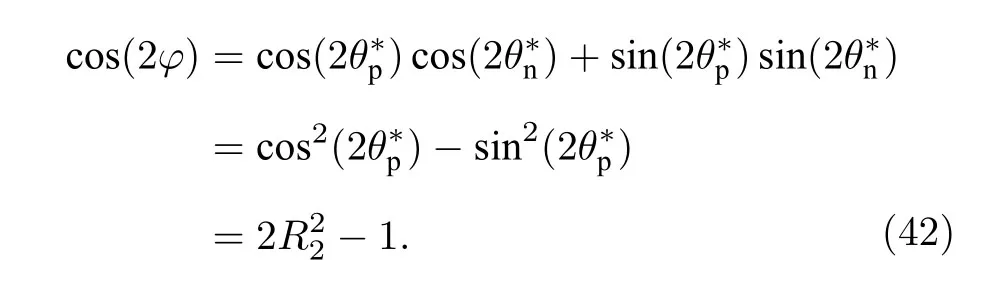

3.4 一級相變與振蕩態(tài)
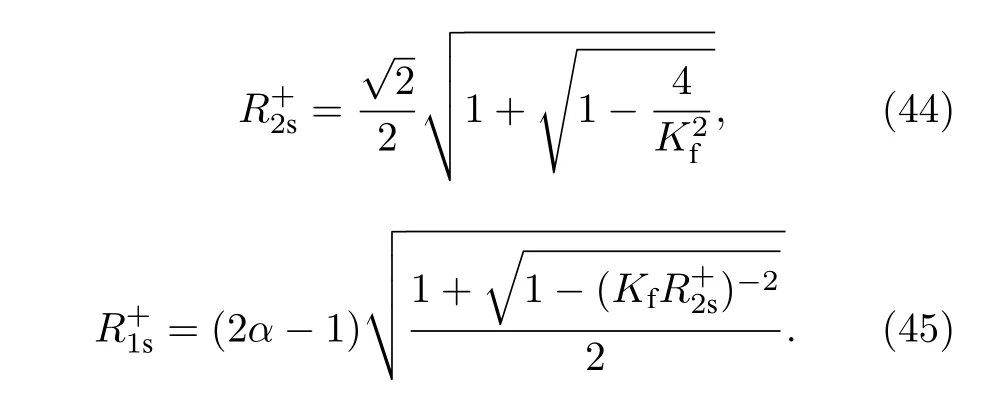

4 結(jié)論

