基于遺傳優化的數據庫丟失數據恢復重構仿真

薛小燕，趙生光，程 剛*，劉宏偉

(1.華北科技學院計算機學院，河北廊坊 065201；2.燕京理工學院，河北廊坊 065201；3.青海民族大學土木與交通學院，青海西寧 810007)

1 引言

網絡數據存儲量的急速上升與用戶需求的復雜化令數據庫建設規模與使用范圍大幅提升[1]。在此大環境下，不同數據庫攻擊方法層出不窮，由數據庫攻擊或計算機網絡中的軟、硬件故障以及網絡故障等導致數據庫被破壞，數據庫內數據丟失的問題屢見不鮮[2]。數據庫中數據的可靠性與準確性是數據庫構建的基礎要求，為保障數據庫內數據的可靠性與準確性，研究一種用于數據庫丟失數據恢復重構的方法極為重要。

文獻[3]提出分布式數據庫用戶丟失數據恢復重構仿真，通過遺傳算法計算出丟失數據的最優參數，利用熵值的思想計算加權系數，最終獲得分布式數據庫丟失數據的填充值。實驗證明該方法對于數據恢復的精度較高。但目前該領域使用最為普遍的數據庫丟失數據恢復重構方法為構建丟失數據判斷模型，利用判斷模型判斷丟失重聚，實現丟失數據恢復重構。文獻[4]提出基于改進壓縮感知算法的方法通過構建完備字典，生成丟失數據丟失項取樣矩陣，將其作為壓縮感知框架的測量矩陣，通過正則化正交匹配追蹤實現數據恢復重構。文獻[5]提出基于模態傅里葉-支持向量機優化的方法構建粒子群優化最小二乘支持向量機模型，利用傅里葉修正集合模態分解的數據序列取得更佳的擬合效果。但上述數據庫丟失數據恢復重構方法實際應用過程中直接應用在隨機丟失模式下，導致恢復重構準確率較低，不適用于大規模數據集。

基于此提出基于遺傳優化的數據庫丟失數據恢復重構方法，并通過仿真驗證所提方法的性能優勢。

2 數據庫丟失數據恢復重構方法

2.1 支持向量機輸入輸出確定及處理

以實現數據庫丟失數據恢復重構為目的，綜合考慮數據庫內丟失數據與時間、空間等不同因素的相關性[6]，構建支持向量機多輸入單輸出判斷模型，用于恢復重構數據庫內某一時刻丟失的數據。

支持向量機判斷模型內的多個輸入主要有：丟失數據前一時刻的數據、丟失數據所在的矩陣的行和列等。支持向量機判斷模型內的單個輸出為數據庫丟失數據判斷值。利用數據庫內數據訓練支持向量機判斷模型，獲取模型并保存輸入自變量與輸出因變量間的非線性映射相關性，將其作為數據庫丟失數據判斷器。在數據庫出現數據丟失現象時，在判斷模型內輸入相關數據，即可完成數據庫丟失數據的恢復重構性判斷。

在利用數據庫內相關數據訓練支持向量機判斷模型獲取丟失數據判斷值前需對相關數據實施歸一化處理[7]，公式如式(1)

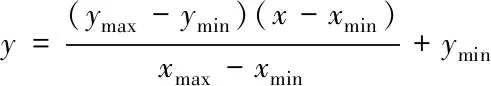
(1)

式(1)內，y和x分別表示歸一化后的數據和歸一化前的數據，ymax和ymin分別表示設定的歸一化后數據上限值和下限值，xmax和xmin分別表示數據庫內數據的上限值和下限值。如果xmax值與xmin值完全一致，也就是數據庫內數據一致，即可確定y值與ymin值一致。經由數次測試后確定，設置輸入自變量的歸一化波動范圍和輸出因變量的歸一化波動范圍分別為1與-1之間和1與0之間，支持向量機判斷模型的判斷結果更符合實際情況。

2.2 支持向量機核函數選取

作為初始數據樣本空間到特征空間的隱式映射，支持向量機核函數的核心是實現初始空間內線性不可分問題與高維特征空間內線性可分問題的轉換[8]。在支持向量機處理回歸判斷問題過程中，核函數設定是否恰當直接影響支持向量機判斷結果的準確性。相關文獻研究結果顯示在求解非線性多因素判斷問題過程中，支持向量機判斷模型采用RBF核函數(Radial Basis Function Kernel，徑向基函數)進行判斷時所得結果的準確性顯著高于其它核函數。基于此，在利用支持向量機判斷模型判斷數據庫丟失數據過程中，支持向量機判斷模型的核函數選取RBF核函數，具體公式描述如式(2)

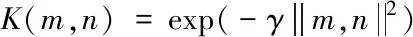
(2)

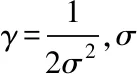
2.3 支持向量機參數尋優

支持向量機判斷模型中懲罰函參數ξ、核函數參數γ與不敏感損失函數參數φ等選擇對于最終獲取結果產生直接影響，為獲取最優支持向量機判斷模型參數，采用遺傳優化算法優化模型參數。

作為全局優化算法，遺傳算法的性能尤為優越，但傳統遺傳算法在實際應用過程中存在計算量較大，實時性較差等缺陷。針對傳統遺傳算法應用中的缺陷，利用Nelder-Mead單純形法對傳統遺傳算法進行優化。

作為一種典型的確定性局部尋優算法，Nelder-Mead單純形法可通過較快的速度收斂至局部極小點[9]。為實現Nelder-Mead單純形法對傳統遺傳算法的優化，將Nelder-Mead單純形法的初始值設定為傳統遺傳算法進化至某代的最優個體，在傳統遺傳算法進化過程中引入Nelder-Mead單純形法，將其作為局部搜索算子。利用Nelder-Mead單純形法優化傳統遺傳算法的詳細過程：

在傳統遺傳算法進化至一定代數SGen的條件下，在群體的最優個體周邊利用Nelder-Mead單純形法實施局部搜索，若Nelder-Mead單純形法搜索過程中未獲取更優點，即定義搜索完成完成，返回進化過程；若Nelder-Mead單純形法搜索過程中發現更優點，即視此更優點為一個個體，以其取代群體內的最差個體[10]。之后，遺傳算法進化過程依據此局部搜索算子融入的方式繼續進行，直至滿足終止條件。

遺傳優化算法主要操作過程：

過程1：選取實數編碼方式對個體實施編碼。

在數據庫丟失數據恢復重構過程中，單個個體由M個基因組成，M為自適應權值，即待優化參數的數量。不同基因值可通過0～2π范圍內的實數描述。在初始化過程中，不同基因取值范圍均在這一區間內[11]。

過程2：利用確定式采樣選擇方式選擇算子。

用Qs表示群體內不同個體在下一代群體內的期望生存數目，公式描述如式(3)

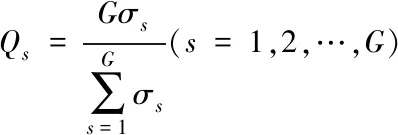
(3)

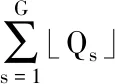
過程3：利用非均勻算術較差法確定交叉算子，通過兩個個體的線性組合獲取兩個新的個體。

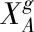
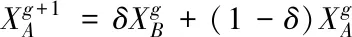
(4)

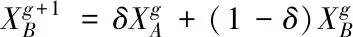
(5)

式(4)和式(5)內，δ表示以參數，其取值范圍為[0，1]。

過程4：利用高斯變異方法確定變異算子。

通過高斯變異的方法確定變異算子能夠優化傳統遺傳算法對重點搜索區域的局部搜索性能。高斯變異的方法即變異操作過程中利用滿足正態分布的隨機數取代當前基因值[12]。

過程5：設定優化過程終止條件

群體內的最佳適應度滿足設定標準，或算法迭代次數達到設定上限值。

依據上述過程中的遺傳操作，設計如圖1所示的遺傳優化算法流程。

圖1 遺傳算法優化流程

2.4 丟失數據判斷

利用遺傳優化算法確定支持向量機判斷模型最優參數后，可將優化后的懲罰函參數ξ、核函數參數γ與不敏感損失函數參數φ等與訓練集代入訓練函數實施訓練，由此構建支持向量機判斷模型。構建測試集與訓練集，利用測試集對此判斷模型實施測試評價，實現數據庫丟失數據恢復重構性判斷。通過該模型實現恢復重構性判斷過程中，測試集不同樣本內前一時刻的數據屬性為上一樣本的數據判斷結果，也就是根據前一時刻的數據判斷結果，結合當前時刻其它屬性判斷當前時刻數據值，該問題可理解為一個典型時間序列判斷問題。

圖2所示為基于遺傳優化的數據庫丟失數據恢復重構算法流程。

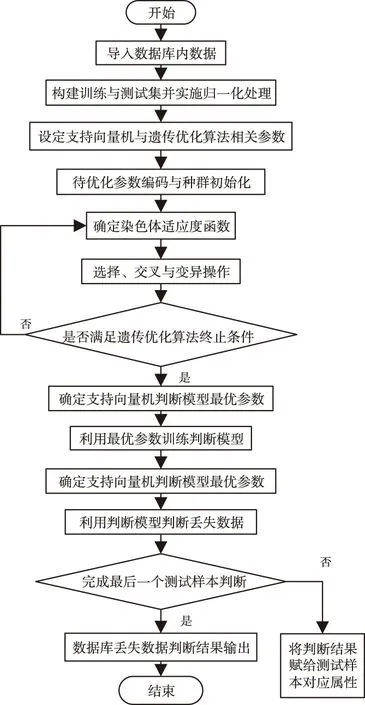
圖2 數據庫丟失數據恢復重構流程

3 實驗分析

實驗為測試本文所提出的基于遺傳優化的數據庫丟失數據恢復重構方法的綜合使用性能，采用仿真的方式進行數據庫丟失數據恢復重構測試，同時對比本文方法與其它兩種對比方法(文獻[4]方法為對比方法1，文獻[5]方法為對比方法2)的性能。數據庫丟失數據恢復重構實驗選取某實驗室環境檢測信息數據庫為仿真對象，以Windows XP和Matlab R 2009A 軟件分別作為仿真環境與仿真平臺。數據庫丟失數據恢復重構實驗所使用的計算機CPU和內存分別為E7500 2.93GHz和4GB。得出具體仿真過程與仿真結果。

3.1 仿真參數設定

所提方法中利用遺傳優化算法選取支持向量機判斷模型最優參數的過程對于最終丟失數據恢復重構結果產生重要影響。相關參數設定如表1所示。

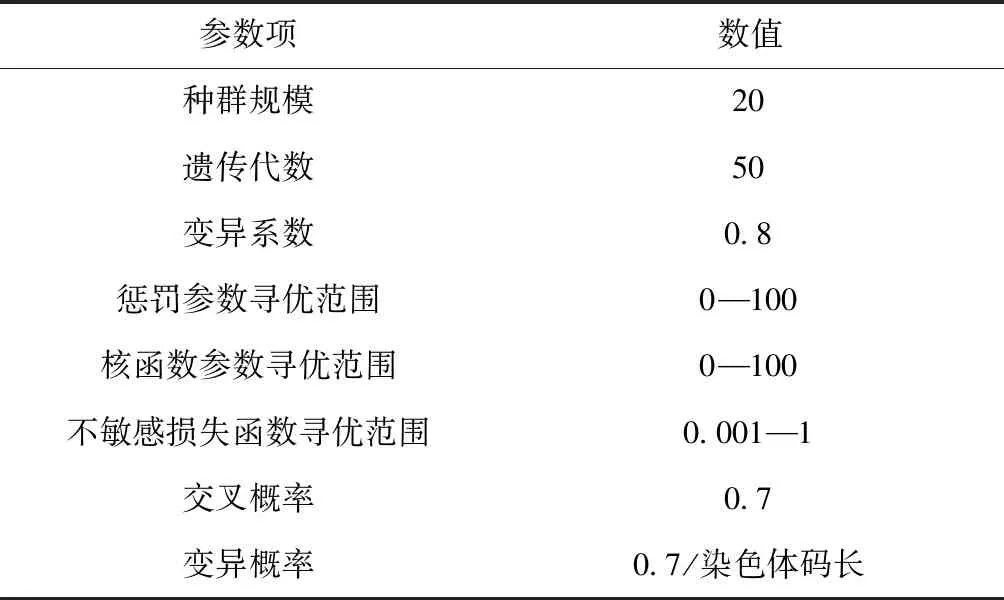
表1 參數設定

3.2 參數尋優仿真

選取5折交叉驗證。通過測試確定最優判斷模型對應支持向量機參數尋優結果為：懲罰參數、核函數參數和不敏感損失函數分別為31.879、0.117和0.046。表2所示為參數尋優進化過程。

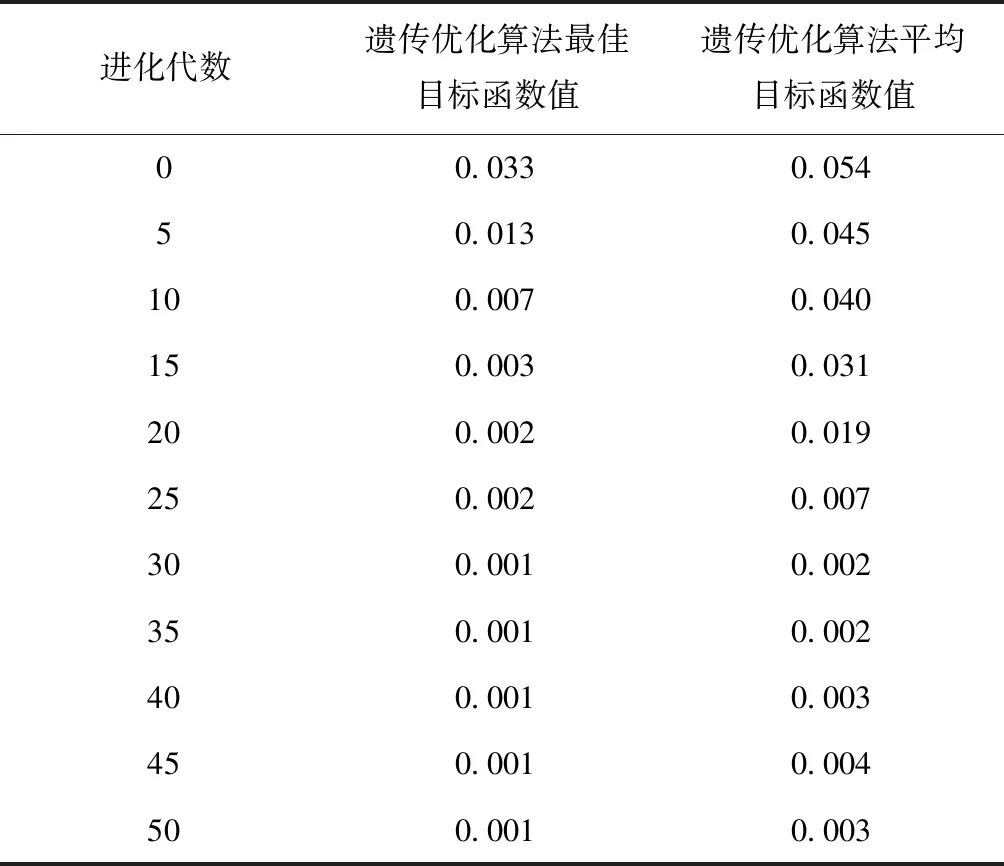
表2 參數尋優進化過程

分析表2得到，采用所提方法進行數據庫丟失數據恢復重構時，遺傳優化算法進化前期獲取的最優目標函數值相較于平均目標函數值具有明顯差異；進化后期的獲取的最優目標函數值同平均目標函數值相比較為接近。產生這種現象的主要原因在于所提方法中在設計適應度函數時引入Metropolis判斷標準的選擇復制策略。在進化前期，各染色體相對的適應度函數值一致度較高，具有較強的劣質解接收能力，可確保遺傳優化過程中的種群多樣性，防止出現早熟問題。在進化后期，優質染色體對應的適應度函數值顯著提升，可提升所提方法參數尋優過程的收斂速度。

3.3 丟失數據恢復重構仿真結果

將上一實驗中獲取的最優懲罰參數、最優核函數參數、最優不敏感損失函數和訓練集代入訓練函數，通過訓練后得到支持向量機判斷模型。利用該模型進行數據庫丟失數據恢復重構，所得結果如圖3所示。

圖3 丟失數據恢復重構仿真結果

分析圖3得到，采用所提方法恢復重構仿真對象內丟失數據，可較好的地擬合訓練集，均方誤差控制在0.01%。

采用訓練好的模型對驗證測試集，選取相對誤差作為丟失數據恢復重構性能的評價指標。測試集仿真結果如圖4所示。

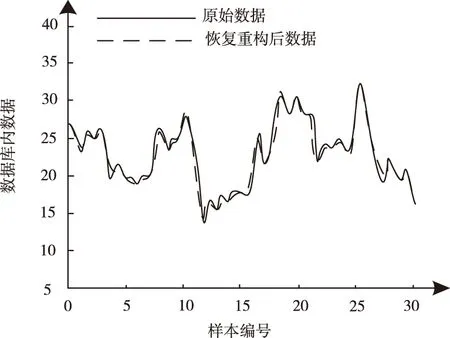
圖4 測試集仿真結果

分析圖4得到，所提方法對測試集中丟失數據實施恢復重構時，相對誤差上限值為5.58%，相對誤差下限值為0.00%，平均相對誤差為1.76%。以上仿真結果充分說明所提方法能夠有效、準確恢復重構仿真對象中丟失數據。

3.4 仿真結果對比

對比所提方法、方法1與方法2針對仿真對象中丟失數據的恢復重構結果，以此說明本文方法的性能優勢。

圖5所示為所提方法、方法1與方法2進行仿真對象丟失數據恢復重構過程中，不同方法各項評價對標對比結果。

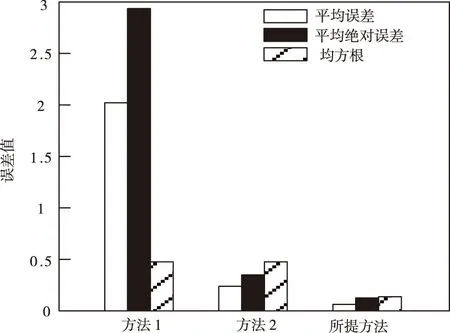
圖5 不同方法仿真結果對比

分析圖5得到，采用所提方法對仿真對象內丟失數據實施恢復重構的結果與兩種對比方法相比，誤差更小，更接近與仿真軟件模擬的仿真對象實際數據，由此說明本文方法恢復重構的丟失數據準確度更高。

4 結論

所提方法基于遺傳優化進行數據庫丟失數據恢復重構，構建用于丟失數據恢復重構的判斷模型，利用遺傳優化算法獲取模型最優參數。仿真結果顯示所提方法不僅能夠有效恢復重構數據庫內丟失數據且顯著提升丟失數據恢復重構的準確度，具有較大推廣價值。但由于條件限制，存在一定局限性，后續工作可以提升優化參數對復雜數據的處理效率，豐富該領域的研究。