溫差電器件內阻影響因素分析

孫夏爽，段玥晨，楊號南

(1.鄭州大學機械與動力工程學院，河南鄭州 450001；2.河南省智能制造研究院，河南鄭州 450001)

溫差發電技術利用熱電半導體材料的溫差電效應將熱能直接轉換為電能，具有壽命長、結構緊湊、可靠性高等優點，尤其適用于空間或深海裝置能量轉換等特殊工況[1]。溫差發電技術應用于很多領域，目前研究較多的方向是航天方面的同位素溫差電池、汽車尾氣余熱溫差發電電池[2-3]。影響熱電器件性能的主要因素包括熱電材料的優值系數、塞貝克系數、電導率和熱導率。其中塞貝克系數、電導率和熱導率的數值都是關于溫度的函數，所以熱電器件材料性能取決于溫差電器件中的溫度分布，溫差電器件的內阻也隨著溫度的變化而變化。文獻[4]將溫差電器件假設為單一勻質材料，材料中溫度分布為線性分布，通過仿真發現熱電臂中溫度分布不是線性分布，并差別較大。文獻[5]對Half-Hesuler 熱電偶用COMSOL 軟件對溫差電器件進行仿真分析，其中求解了熱電偶的內阻，但其數據范圍較小，無法直觀看出內阻與電路電流的關系。本文使用COMSOL 軟件對溫差電器件進行有限元仿真，分析溫差電器件內阻的影響因素及溫差電器件內阻變化對溫差電器件輸出功率和轉換效率的影響。

1 計算模型

溫差電效應是指溫差電器件兩端存在溫差時，冷熱兩端會產生電動勢。外接電路后溫差電器件可成為電源，如圖1所示。

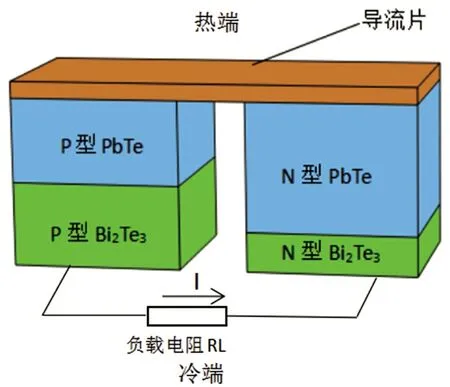
圖1 溫差發電裝置

溫差發電裝置主要是依靠塞貝克效應產生電動勢。溫差發電過程中還伴隨著帕爾貼效應、傅里葉效應、焦耳效應和湯姆遜效應。式(1)～(4)分別表示塞貝克效應、帕爾貼效應、傅里葉效應和焦耳效應[6]。

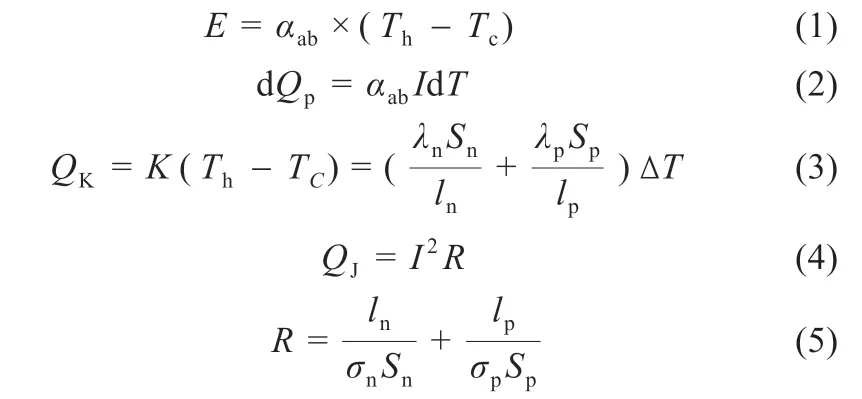
式中：E為電源電動勢；αab為塞貝克系數；Th為熱端溫度；Tc為冷端溫度；Qp為帕爾貼熱；I為電流；Qk為傅里葉熱；K為熱導；λ 為熱導率；S為熱電臂截面積；l為熱電臂高度；QJ為焦耳熱；R為溫差電器件內阻；ρ 為電阻率。

溫差電器件的最大輸出功率如式(6)[7]：

式中：RL為負載電阻；Qh為熱電器件輸入功率；η 為轉換效率。

在溫差發電過程中，電路外接負載電阻后，熱電器件內部會產生電流，溫差電器件內部的電流會重新影響到溫差電器件內部的溫度分布，進而影響熱電臂的材料參數。熱電臂溫度分布與電流的關系如式(8)～(9)所示[8]：

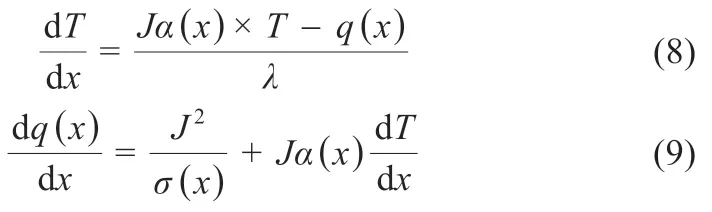
式中：J為電流密度。

由于關系過于復雜，以往學者分析過程中往往對熱電臂中的溫度分布分析進行省略，以線性分布代替。本文通過仿真求得電源內阻與電路電流的曲線圖，發現電路電流的大小對溫差電器件的內阻也有很大的影響。電流I可由負載電阻RL換算得出，如式(10)所示。為了使仿真結果表達清晰，本文將使用電路電流作為變量代替負載電阻進行分析。

2 有限元模型建立

本文對寬溫域的溫差電器件進行分析，故采用分段式熱電臂的結構模型進行仿真分析。高溫端采用PbTe 材料，其中P 型 PbTe 材料為 K0.02Pb0.98Te[9]，N 型 PbTe 材料為PbTe0.998I0.002[10]。低溫端采用Bi2Te3材料，其中P型Bi2Te3材料為Bi0.3Sb1.7Te3[11]，N 型Bi2Te3材料為Bi2Te2.7Te0.3[10]。采 用ZT值 交點方法確定P 型和N 型熱電臂中各材料占比[4]，計算得P 型熱電臂材料分界面溫度為530.6 K，Bi2Te3占比為57.115 7%，N 型熱電臂材料分界面溫度為455 K，Bi2Te3占比為26.988 8%。通過對比分析，熱電臂截面形狀采用正方形[12]。熱電偶模型尺寸見表1。在COMSOL軟件中創建仿真模型如圖2 所示。

表1 熱電偶模型尺寸 mm

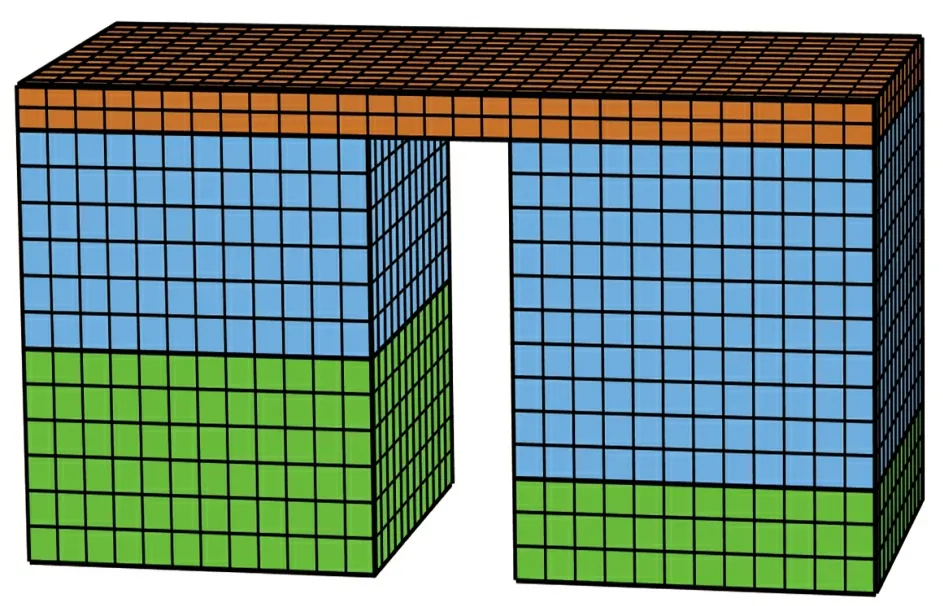
圖2 有限元模型

為了對仿真過程進行簡化，對模型有如下假設：(1) 熱電壁側面絕緣，熱傳導沿著熱電壁的長度方向；(2) 忽略熱電器件與環境的熱交換；(3)忽略材料間接觸熱阻和接觸電阻的影響；(4)忽略熱電臂中的焊料層。

在COMSOL 軟件仿真過程中，先添加邊界條件，再進行網格劃分，模型的網格采用較細化劃分方法，使用掃掠的方法建立網格[13]。COMSOL 軟件仿真過程中用外加電流代替負載電阻的變化。

3 有限元仿真結果分析

當熱端溫度為650 K，冷端溫度為300 K，沒有負載電阻的情況下，通過有限元軟件仿真之后得到的結果如圖3 所示。這時沒有電流的影響，P 型熱電臂材料分界面溫度為530.6 K，N 型熱電臂材料分界面溫度為455 K，與ZT值交點法求得的材料分界面溫度一樣。

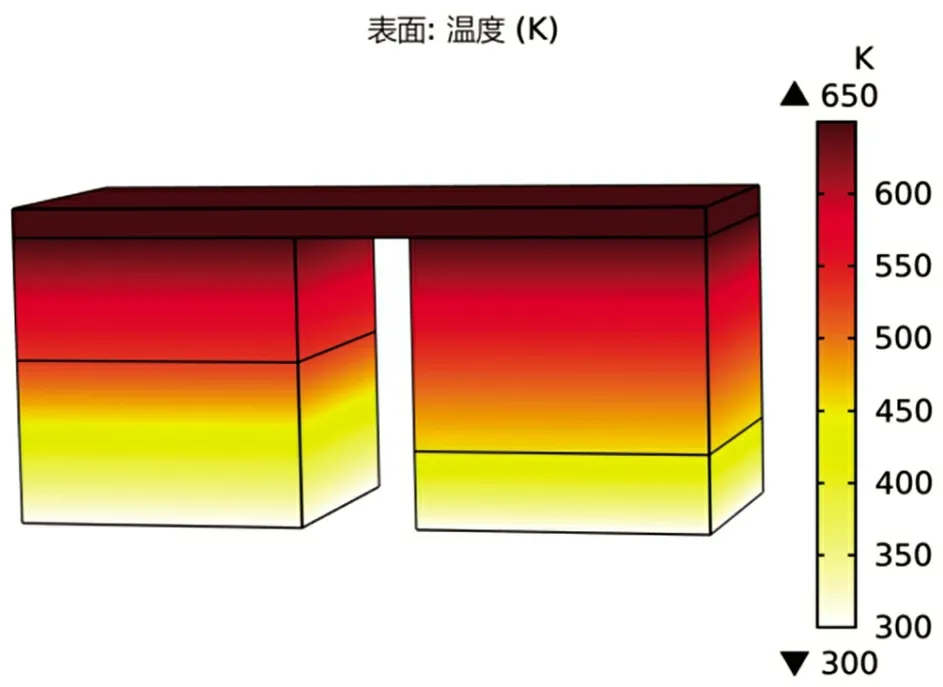
圖3 開路時仿真結果

3.1 電路電流對內阻的影響

在該分析中選取熱端溫度為650 K，冷端溫度為300 K。本次仿真過程中以電路電流為變量，熱電偶內阻、材料分界面溫度、電源電壓、輸出功率、輸入功率和轉換效率為因變量。熱電偶內阻等于輸出電壓與負載電阻圖像的斜率[14]，本文將根據輸出電壓和負載電阻求熱電偶的內阻。為了能夠使圖像表達更簡潔清晰，本小節將以電路電流為變量代替負載電阻進行有限元仿真分析。以電路電流為因變量的有限元仿真分析結構如圖4 所示。

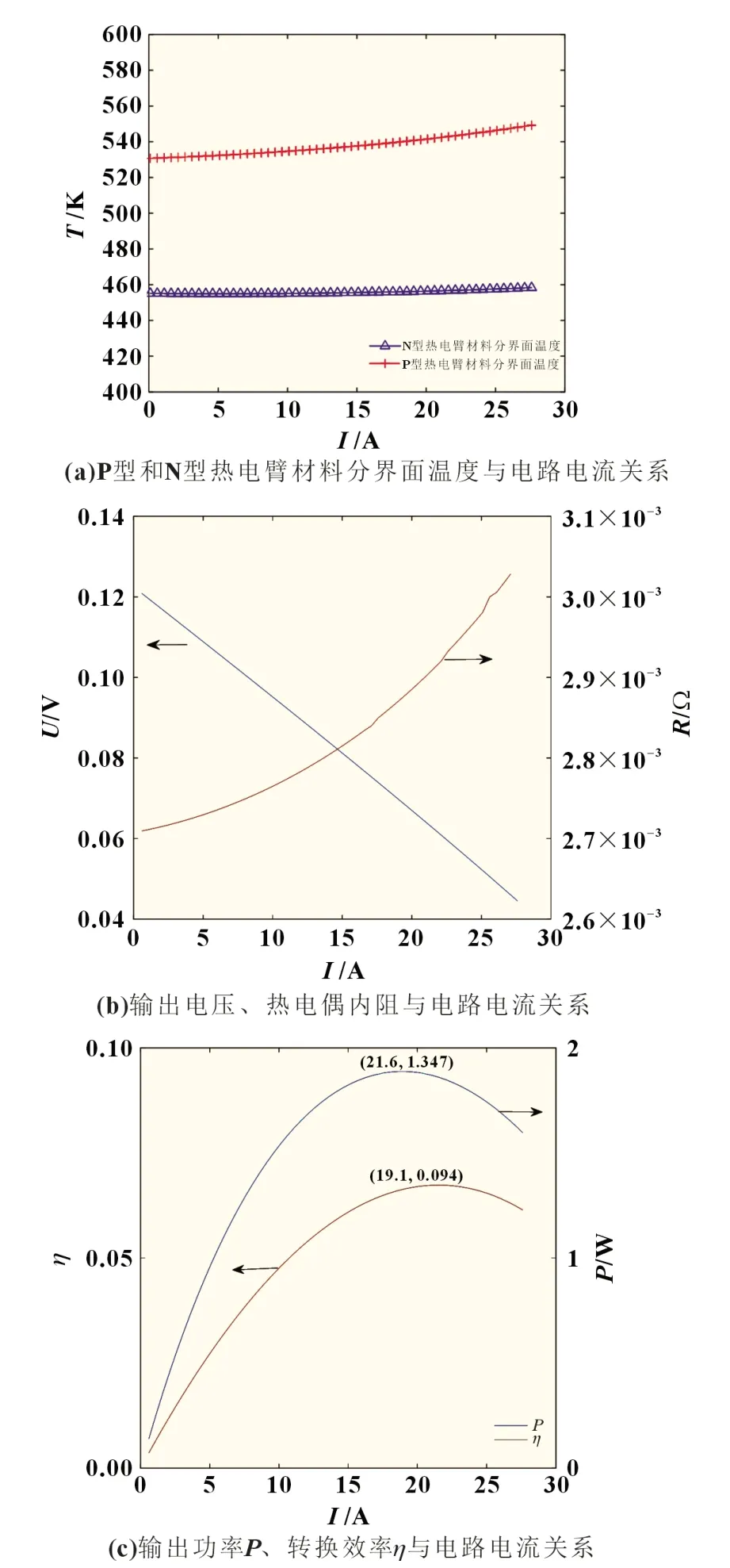
圖4 電路電流為因變量的有限元仿真分析

通過仿真分析的結果可知，熱電偶的開路電壓為122.196 mV，此時熱電偶的內阻為2.708 mΩ。由仿真結果可知，熱電偶的材料分界面溫度是隨著電路電流變化的。熱電偶內阻隨電流的增大而增大，材料分界面溫度隨電流的增大而增大，且P 型熱電臂分界面溫度增長幅度明顯大于N 型熱電臂分界面的溫度增長幅度。輸出電壓隨電流的增大而減小，當電流等于21.6 A 時，熱電偶取得最大輸出功率1.347 W，此時熱電偶內阻為2.911 mΩ，相比開路時增加了7.5%。當電流等于19.1 A 時，熱電偶取得最大轉換效率9.40%，此時熱電偶內阻為2.871 mΩ，相比開路時增加了6.06%。仿真結果如表2 所示。

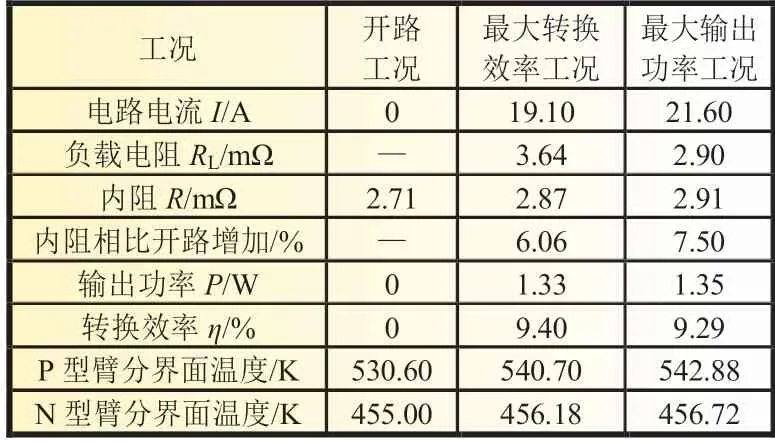
表2 以負載電阻為因變量仿真結果

3.2 尺寸因子對內阻的影響

尺寸因子G為熱電臂截面積與熱電臂長度之比。尺寸因子G影響熱電偶的內阻及熱導，隨著尺寸因子G的增加，熱電偶的內阻會減小，熱導會增加。本小節保持熱電臂中各材料所占比例，設置3 組不同的尺寸因子，觀察熱電偶的內阻隨尺寸因子的變化規律。仿真過程中固定熱電臂截面積，通過改變熱電臂長度來改變尺寸因子。本文用熱電臂長度L為10、15 和20 mm 三組數據進行仿真分析，有限元仿真分析結果如圖5 所示。

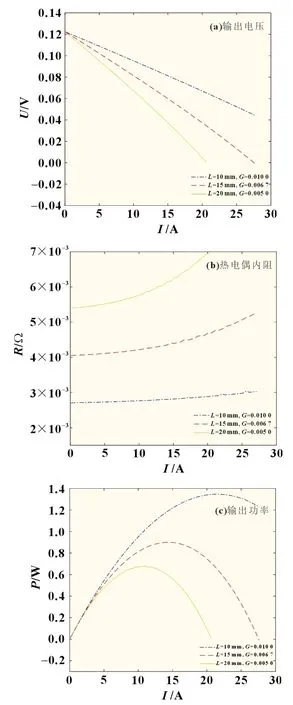
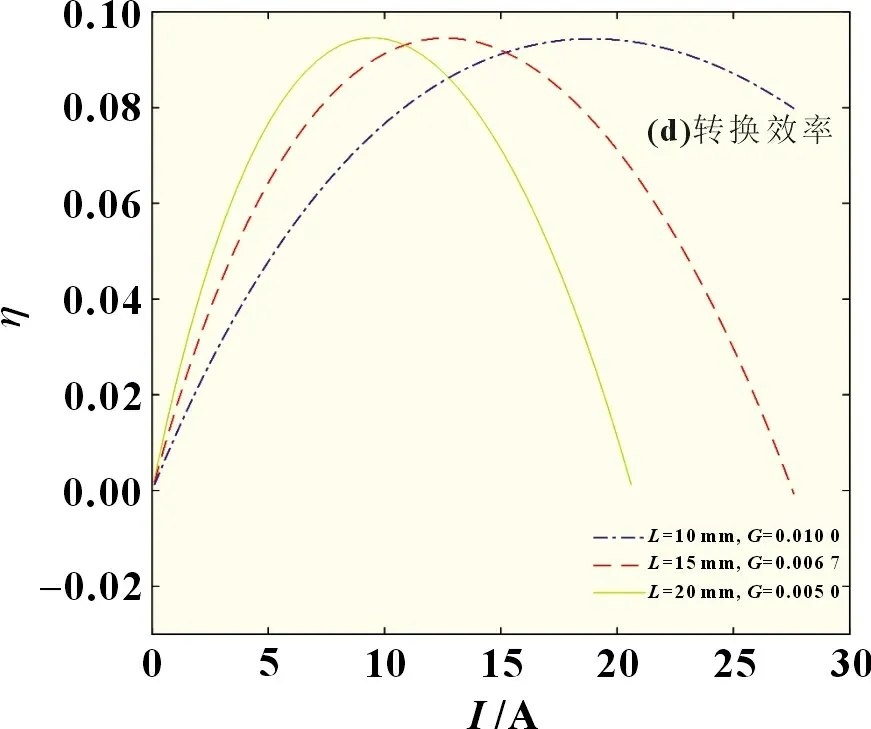
圖5 尺寸因子為變量的有限元仿真結果

仿真結果整理如表3 所示。通過仿真分析的結果可知，熱電偶內阻與尺寸因子有很大關系。隨著尺寸因子增加，熱電偶內阻會減小，熱電偶內阻隨電流的變化會減小。這說明尺寸因子越大對熱電偶內阻值影響越小。同時發現隨著尺寸因子的增加，熱電偶的最大輸出功率會增大，其所對應的電路電流也會增大。但是，尺寸因子的變化對熱電轉換效率影響不大，三組不同尺寸因子的熱電偶其最大熱電轉換效率相差不大，但最大熱電轉換效率所對應的電路隨著尺寸因子的增大而增大。

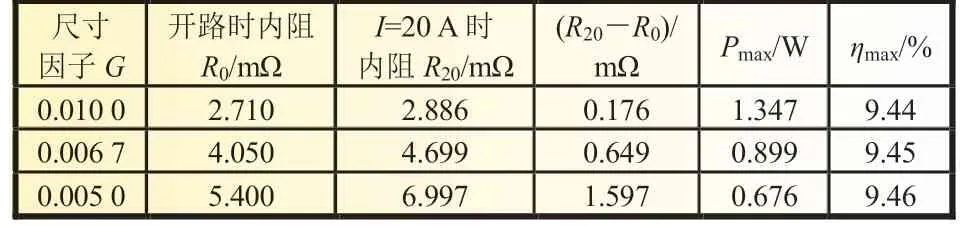
表3 不同尺寸因子熱電偶仿真結果

3.3 冷熱端溫差對內阻的影響

溫差為熱端與冷端溫度之差。本文固定冷端溫度為300 K，設置三組熱端溫度分別為600、650 和700 K，冷熱端溫差分別為300、350 和400 K。以熱端溫度為變量，來探究冷熱端溫差對熱電偶的影響。COMSOL 軟件有限元仿真分析結果如圖6 所示。

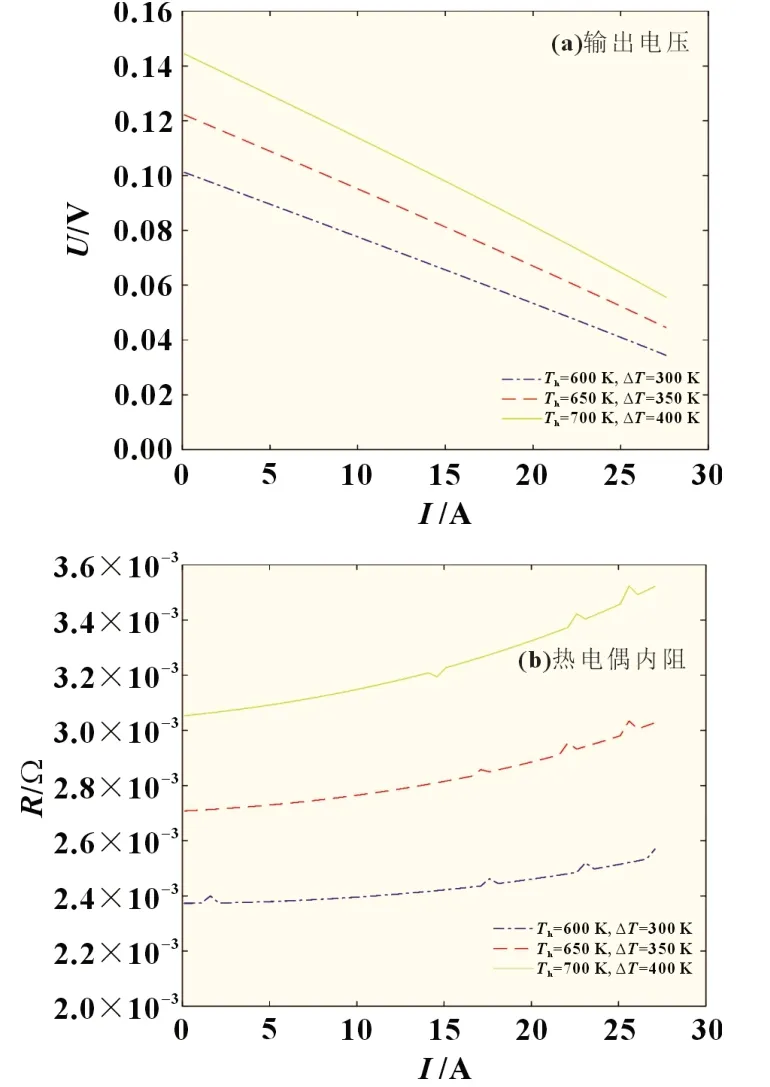
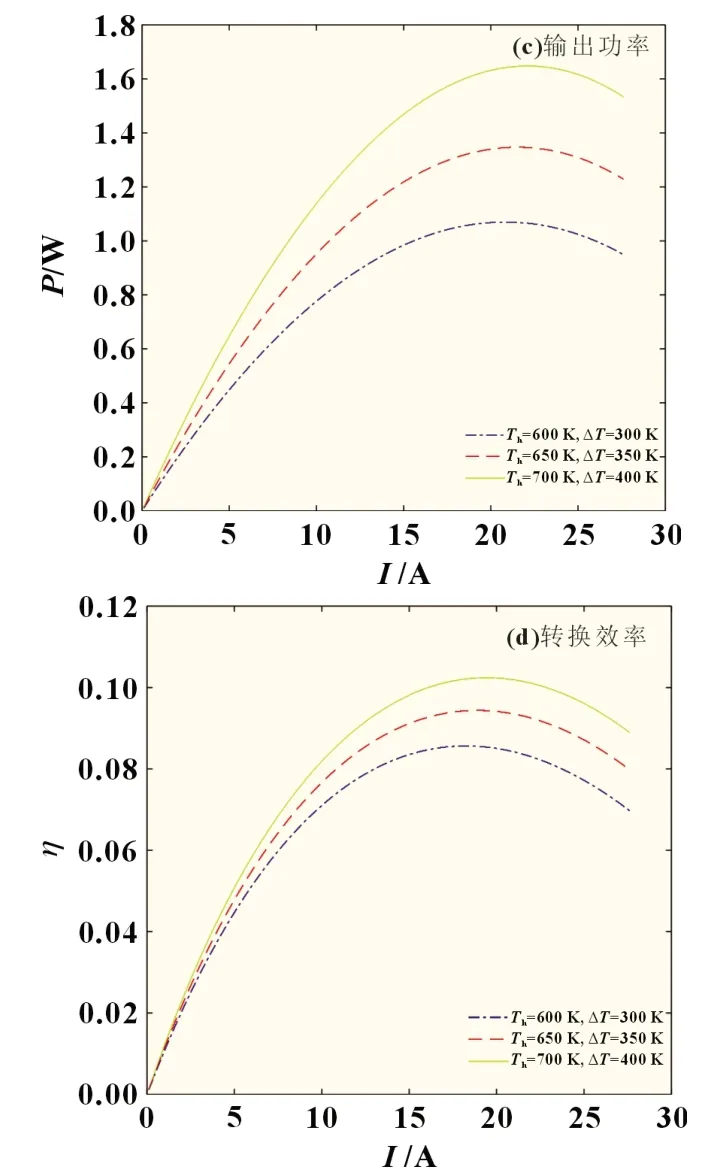
圖6 溫差為變量的有限元仿真結果

仿真結果整理如表4 所示。通過仿真分析的結果可知，隨著溫差增大，熱電偶開路時的內阻也會增大，同時電流對熱電偶內阻的影響也會變大，如圖6(b)所示。三種工況的最大輸出功率和最大轉換效率都隨溫差的增大而增大，如圖6(c)和(d)所示。由圖可知，隨著溫差增大，最大輸出功率和最大轉換效率所對應的電流沒有太大變化。

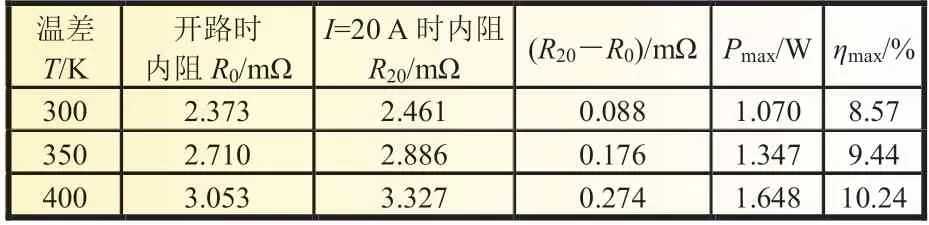
表4 不同溫差熱電偶仿真結果

4 結論

本文對由PbTe 和Bi2Te3兩種材料組成的寬溫域熱電材料進行有限元仿真，分析了溫差電器件內阻的影響因素。通過仿真結果得出如下結論：(1)隨著負載電阻的減小，電路電流的增大，熱電偶的內阻呈增加的趨勢，在本文設計模型中，當電流達到20 A 時，熱電偶內阻相比開路時增加了0.176 mΩ，增加了6.5%。由此可見，電路中電路電流對熱電偶內阻的影響很大，不可忽略。(2)通過以溫差電器件的熱電臂尺寸因子為變量進行有限元仿真分析，尺寸因子為0.01 時，當電流20 A 時，熱電偶內阻比開路時熱電偶內阻增加了6.5%。尺寸因子為0.005 時，當電流20 A 時，熱電偶內阻比開路時內阻增加了29.6%。結果表明：尺寸因子越小，熱電偶的內阻越大，同時，電路電流對熱電偶內阻的影響越大。(3)以冷熱端溫差為變量進行有限元仿真分析。溫差為300 K 時，當電流20 A 時，熱電偶內阻比開路時熱電偶內阻增加了3.7%。溫差為300 K時，當電流20 A 時，熱電偶內阻比開路時內阻增加了8.97%。，結果表明：熱電偶溫差越大，開路電阻越大，電路電流對熱電偶內阻的影響越大。(4)通過對比發現，相對與溫差的改變，尺寸因子的改變對熱電偶的內阻影響更大。