橋梁荷載試驗加載效率合理范圍研究
劉 鵬,張建東,,劉 朵,王賢強
(1.南京工業大學土木工程學院,江蘇 南京 211816;2.蘇交科集團股份有限公司,江蘇 南京 211112)
0 引 言
荷載試驗是檢驗橋梁實際承載能力是否符合標準要求不可或缺的方法和步驟。一般地,橋梁荷載試驗前需要確定加載效率,通過有限元軟件計算分析包絡線和控制截面影響線,以單一的彎矩(或撓度)加載效率控制為準,進行車輛數量或軸重、位置、車距的調試。但是,僅以彎矩(或撓度)加載效率控制在在0.85~1.05時,撓度(或彎矩)效率達不到0.85或者超過1.05,往往出現無法合理反映橋梁整體剛度狀況。
對于加載效率取值研究,任東華等學者從可靠度角度出發,使用考慮抗力衰減的荷載試驗方法,確定加載效率界限方法;
刑兵等人提出了根據設計荷載不同組合方法計算加載效率及其系數的建議;石雄偉等人首次提出從動力增大系數角度來考慮舊、新荷載加載效率取值影響。現有研究以及《公路橋梁荷載試驗規程》(JTG/T J21-01―2015)基本是基于單一的效率控制方法,未考慮兩者加載效率控制方式關系,存在撓度和彎矩加載效率無法同時滿足規范要求的情況。
本文在采用常用車型和布載方法基礎上,利用理論分析與有限元軟件計算相結合的方法,分析撓度加載效率、彎矩加載效率與車輛位置、車距、車重的關系以及兩種加載效率的相互關系。再利用線性回歸分析方法,提出加載效率優化取值,為工程實踐及相關規范修補完善提供借鑒。
1 加載效率計算方法
《公路橋梁荷載試驗規程》(JTG/T J21-01―2015)(以下簡稱“規程”)對于新橋加載效率計算按式(1)計算。
(1)
式中:ηq為加載效率;SS為試驗荷載內力或位移的最大計算效應值;S為控制荷載相應內力或位移最不利效應計算值;μ為按規范取用的沖擊系數。
工程上,通常需要借助橋梁博士、Midas等軟件對上述公式的效應值進行計算。本文以簡支梁橋為例進行定性分析,在規定加載車型和車距的基礎上,無需計算影響線,通過理論公式直接計算出彎矩、撓度,最終得到加載效率。加載車型(或車隊)選用常用的縱向兩輛三軸車,車距為d,后軸軸重為P1,前軸軸重為P2,總軸重為P總=2P1+P2,軸重比為1∶2∶2。
總彎矩或撓度為各個軸重作用的疊加,以某一軸為例,計算其加載效率,控制荷載取設計荷載標準值。其中q=10.5 kN/m,計算跨徑l≥50 m時F=360 kN,l≤50 m時F=2(l+130)kN。以簡支梁橋為例進行分析,控制荷載加載示意圖如圖1所示,試驗荷載車輛加載示意圖如圖2所示,其中b表示車軸與橋梁最近一端的距離。
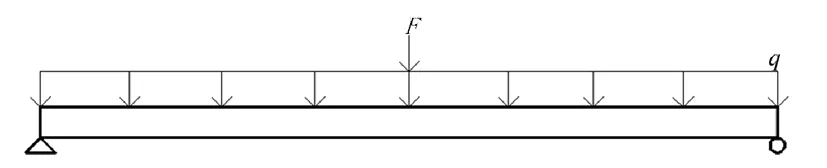
圖1 控制荷載加載示意圖
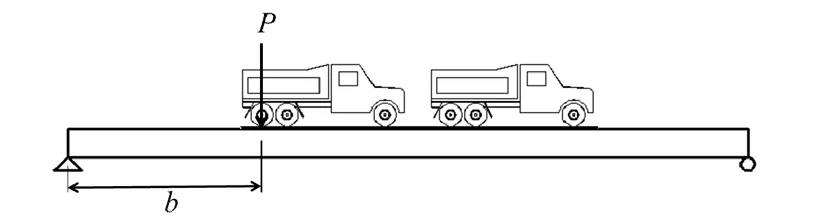
圖2 試驗荷載車輛加載示意圖
以簡支梁橋跨中截面為控制截面,彎矩加載效率計算如式(2),撓度加載效率如式(3),撓度效率與彎矩效率比值如式(4)
(2)
(3)
(4)
式中:ηM、ηw為彎矩加載效率、撓度加載效率;M1、w1為設計荷載作用下的彎矩、撓度控制值;M2、w2為試驗荷載下的彎矩、撓度;P為軸重;l為計算跨徑;η為撓度-彎矩加載效率比值;q、F設計荷載標準值。
對于已知的橋梁,由(2)、(3)可知,加載效率與車輛位置和軸重有關;由式(4)可知,撓度效率與彎矩效率的比值只與車輛位置有關,這與影響線加載方式一致。僅改變車輛軸重時,計算出車輛布置在跨中附近若干位置的彎矩加載效率、撓度加載效率,利用回歸分析方法,將彎矩加載效率與撓度加載效率關系進行線性擬合,不同總軸重撓度-彎矩加載效率關系曲線圖如圖4所示。
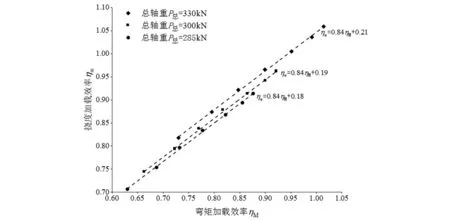
圖3 不同總軸重撓度-彎矩加載效率關系曲線圖
由圖3可知,加載車輛總軸重285 kN、300 kN、330 kN關系曲線斜率均為0.84,截距分別約為0.18、0.19、0.21,截距與總軸重成正比即285∶300∶330=0.18∶0.19∶0.21。由于只改變軸重的情況下可等比例地改變加載效率,而從圖4可知關系曲線斜率不變,截距成比例,關系曲線平移。因此,可利用改變軸重的方法,對于不同的橋梁和車輛位置,都可以使撓度-彎矩加載效率更大概率同時滿足0.85~1.05。
2 撓度-彎矩曲線與車距、跨度關系
2.1 簡支梁撓度-彎矩加載效率關系
由上文分析可知,軸重改變撓度-彎矩效率關系曲線截距,而由式(4)可知車輛位置影響撓度-彎矩效率比值。因此,為了研究加載效率與車輛位置的關系,結合工程實際,固定前車后軸位于控制截面處,只移動后車位置,使車距滿足常用的2.5 m≤d≤6 m,改變車距布載示意圖如圖4所示。
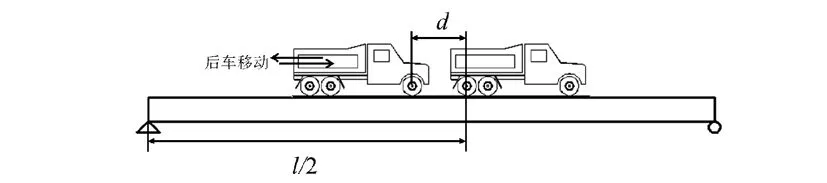
圖4 改變車距布載示意圖
分別計算得出跨度l=40~100 m簡支梁橋跨中截面加載效率與隨車距d變化的值,并將撓度-彎矩加載效率進行線性擬合,不同跨度撓度-彎矩加載效率關系曲線圖如圖5所示。由前文分析可知,通過等比例改變加載車軸重,可調整曲線截距,使得關系曲線經過點(0.85,0.85),調整后撓度-彎矩加載效率關系曲線圖如圖6所示。
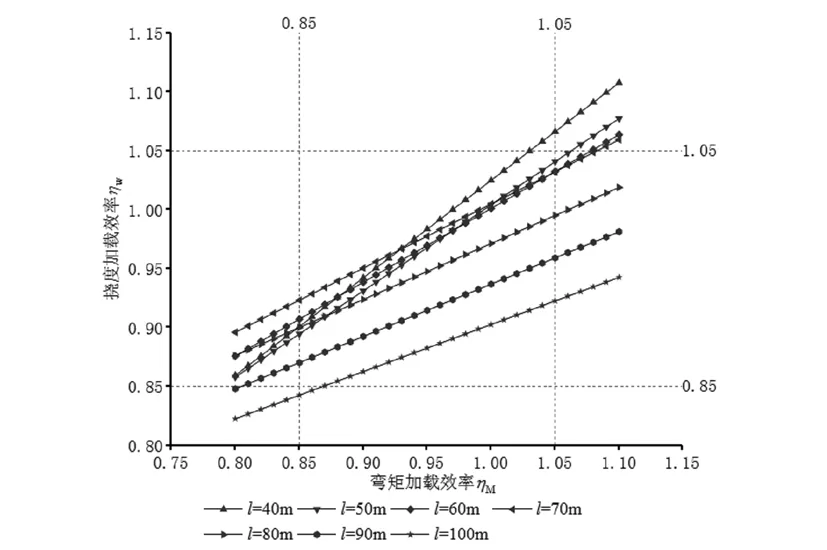
圖5 不同跨度撓度-彎矩加載效率關系曲線圖
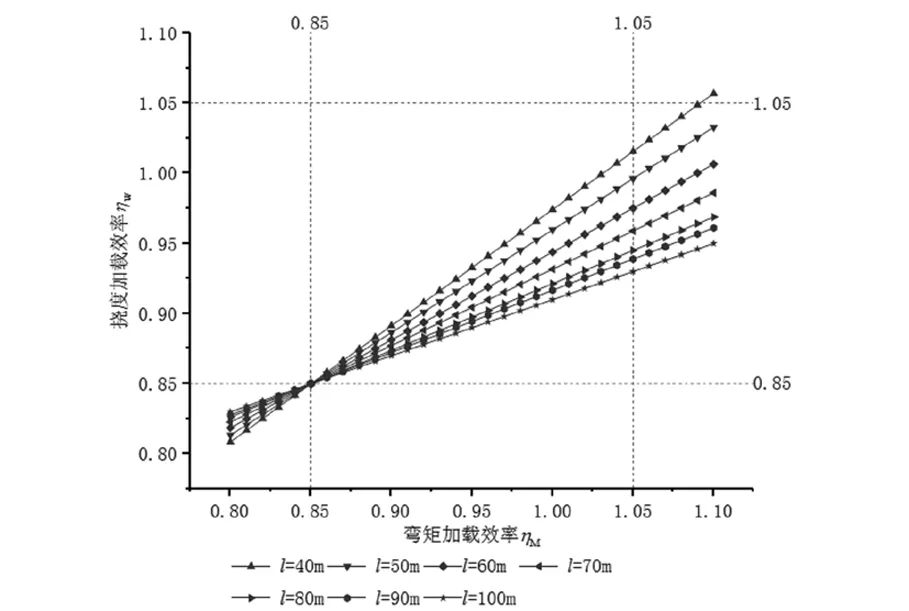
圖6 調整后撓度-彎矩加載效率關系曲線圖
由圖6、圖7可知,只在改變車距時,隨著跨度增加,撓度-彎矩關系曲線斜率減小;當彎矩效率達到上限1.05時,撓度效率最小值在0.90左右,最大值1.08左右;當彎矩加載效率達到下限0.85時,撓度效率最大值0.90左右;當撓度效率達到0.85時,彎矩加載效率小于0.85;當撓度加載效率達到1.05時,彎矩加載效率最小值約1.02,最大值遠遠超過1.05,且最大值隨著跨徑增大而增大,此時,若以撓度加載效率控制荷載試驗荷載,可能導致彎矩超限導致應力超限,偏于不安全。
2.2 連續梁撓度-彎矩加載效率關系
鑒于連續梁彎矩、撓度計算公式比較復雜,算法各不相同。在公式(2)~(4)定性分析的情況下,為了進一步研究連續梁橋梁荷載試驗時彎矩加載效率和撓度加載效率的關系,以及兼顧兩者效率的合理取值范圍,本文選取了跨徑組合為l=(40+40+40)m、(50+50+50)m、(60+60+60)m、(70+70+70)m、(50+80+50)m、(50+90+50)m、(50+100+50)m、(60+110+60)m、(70+120+70)m、(80+130+80)m、(90+140+90)m、(100+150+100)m的12種連續梁進行邊跨跨中、中跨跨中撓度-彎矩加載效率計算分析。
同樣的控制車距在2.5~6 m范圍,以車距為參數進行加載效率計算分析,得到邊跨、中跨的撓度-彎矩加載效率關系曲線如圖7~圖12所示。
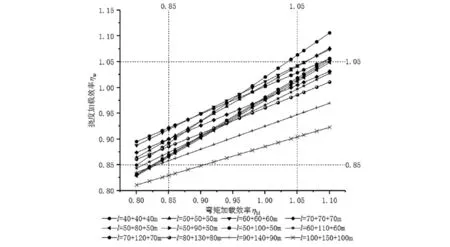
圖7 邊跨撓度-彎矩加載效率關系圖
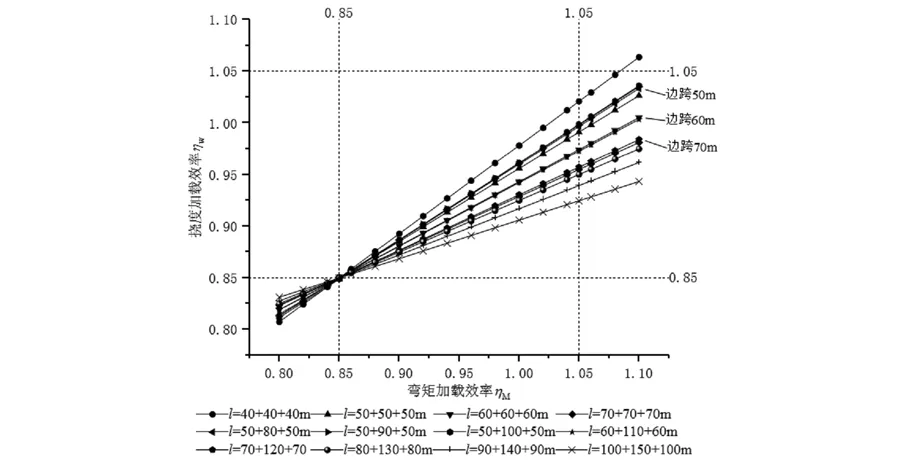
圖8 邊跨調整過0.85撓度-彎矩加載效率關系圖
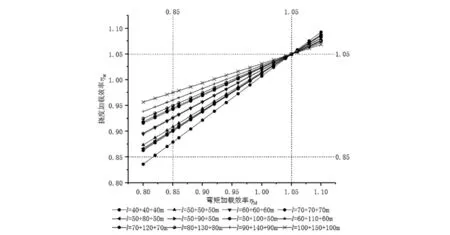
圖9 邊跨調整過1.05撓度-彎矩加載效率關系圖
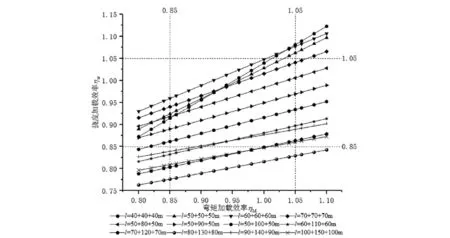
圖10 中跨撓度-彎矩加載效率關系圖
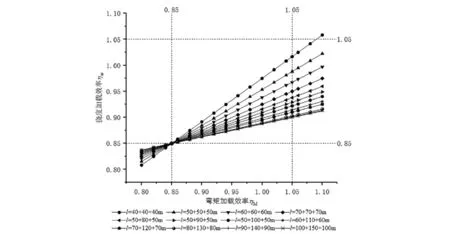
圖11 中跨調整過0.85撓度-彎矩加載效率關系圖
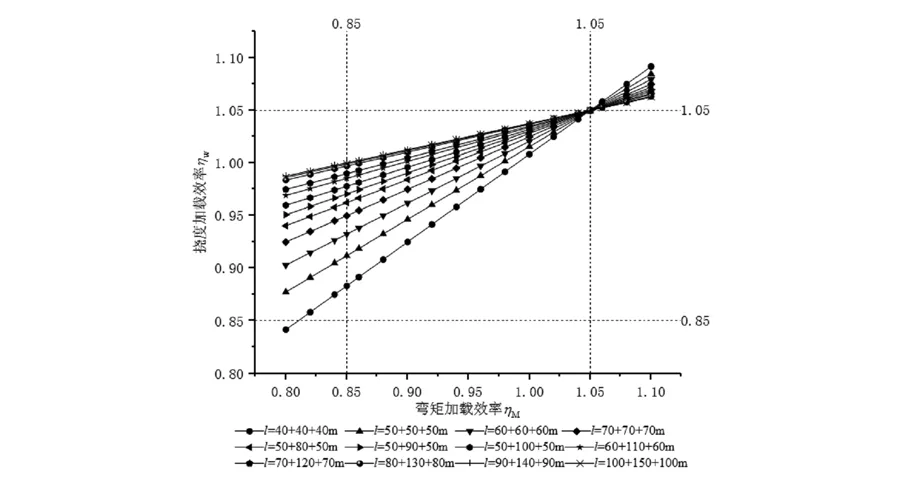
圖12 中跨調整過1.05撓度-彎矩加載效率關系圖
由圖7~12可知,連續梁的撓度-彎矩加載效率曲線規律與簡支梁的一致。由圖7~9可知,具有相同的邊跨跨徑50 m、60 m、70 m撓度-彎矩加載效率關系曲線分別重合,這說明邊跨的加載效率關系與中跨跨度無關,進而說明本文選用的跨徑組合具有一定的普遍適用性。
由圖8、圖11可知,隨著中跨跨度增大,撓度-彎矩加載效率關系曲線斜率減小,當中跨跨度達到140 m以上時,曲線斜率變化較小;如果通過調整軸重使得曲線盡量在0.85~1.05范圍內,當彎矩加載效率達到1.05時,撓度加載效率隨跨度增加趨于0.90,最大為1.05。同樣的,由圖9、圖12可知,通過改變軸重使得關系曲線經過點(1.05,1.05),彎矩加載效率達到0.85時,撓度加載效率在0.85~1.00范圍。
改變荷載試驗加載車軸重和位置,使得彎矩加載效率與撓度加載效率更大概率同時在0.85~1.05范圍內,考慮到撓度-彎矩曲線體現的兩者差異,兼顧撓度-彎矩加載效率,將加載效率取值優化為0.90~1.00。
3 工程實例
以204國道九圩港大橋中三跨連續鋼箱梁橋主橋和簡支鋼箱梁橋引橋為例,兼顧撓度-彎矩加載效率進行布載。連續鋼箱梁跨徑組合為(50+80+50)m,變截面梁高2.0 m~3.2 m。簡支鋼箱梁橋跨徑80 m,梁高3.2 m。兩鋼箱梁橋都為單箱雙室,設計三車道,公路-I級荷載。
所用加載車輛,軸重為(120+120+60)kN,通過改變加載車輛位置和橫向加載車道數量進行加載效率調試,計算出加載車輛在不同位置時控制截面彎矩加載效率及相應的撓度加載效率,各工況不同布載方案(布載示意圖見圖2、圖4)通過調整車距或車輛位置得到滿足要求加載效率。各布載方案加載效率計算結果表見表1。統計兼顧兩者加載效率的取值范圍,得到兼顧撓度-彎矩加載效率取值范圍表見表2。
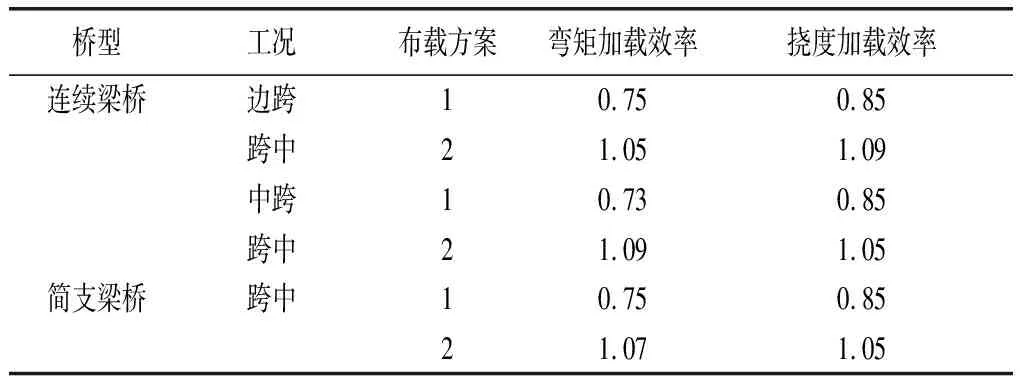
表1 各布載方案加載效率計算結果表
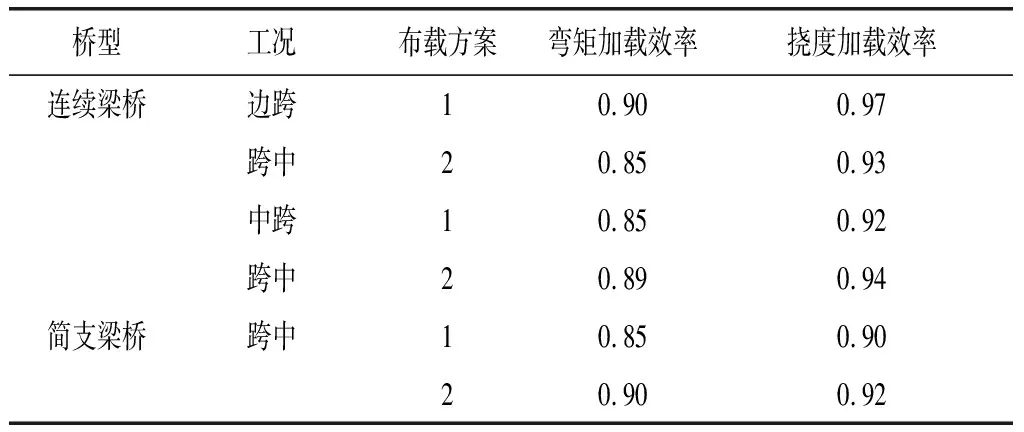
表2 兼顧撓度-彎矩加載效率取值范圍表
由表1可知,以單一控制方法確定的布載方案加載效率往往導致另一加載效率不滿足要求;以撓度加載效率為控制標準取得上限1.05時,彎矩加載效率嚴重超限。因此偏于安全考慮,建議以彎矩控制為主。
由表2可知,兼顧撓度-彎矩加載效率的取值范圍在規程規定的基礎上有所收窄,在某一加載效率取得0.90~1.00時,另一者基本可以滿足規范要求的0.85~1.05,因此取交集得到加載效率取值范圍0.90~1.00。
4 結 論
本文研究了加載效率影響因素及撓度-彎矩加載效率的相互關系,兼顧規程中所提的這兩種加載效率控制方法,并在規程規定的0.85~1.05范圍基礎上進行撓度-彎矩加載效率線性回歸分析,得到以下結論。
(1)撓度加載效率取大值(1.05)時,彎矩效率容易遠大于1.05,而彎矩加載效率取大值(1.05)時,撓度加載效率略超1.05。因此偏于安全考慮,建議以彎矩加載效率控制為主。
(2)對取值進行合理收窄,得到兼顧撓度-彎矩加載效率的優化區間0.90~1.00。
由于本文分析選用了特殊車型,參數分析所用橋梁跨徑未必具有代表性,而且未考慮橋梁梁高、橋寬等特性,對于加載效率取值優化具有一定局限性。因此,需要結合大量的實際的橋梁工程荷載試驗進行更加全面的研究分析,以驗證兼顧撓度-彎矩加載效率的合理取值。

