鋼管桁架節點偏心次應力分析

王 燦

(中設設計集團股份有限公司，江蘇 南京 201104)

0 引 言

理想桁架的桿件僅承受軸力，但在實際工程中的桁架結構則不可避免會承受一部分彎矩和剪力。桁架桿件中由于彎矩和剪力所引起的應力相對于軸力所引起的應力較小，因此稱之為桁架桿件的次應力。當桁架桿件的次應力水平較低時，說明該桁架設計的較為合理，材料利用率較高，桁架的力學性能也就更為優越。現有的桁架次應力的研究均是關于純桁架結構的，而關于帶橋面板的組合桁梁結構的次應力的研究較少。而鋼管組合桁梁橋的工程應用則越來越為廣泛，如國內的干海子大橋，汶川克枯大橋等；國外的Ulla河橋等。因此對于帶橋面板的組合桁梁橋次應力也有必要進行深入研究。

造成次應力的因素有很多，主要的影響因素有節點剛性和節點偏心等。魏慶對全焊鋼橋的次應力進行了研究，對節點剛性的對次應力的影響進行了有限元分析，并根據分析結果給出了相應的設計建議。倪宋健、金輝則分別對空間鋼管桁架和貝雷桁架掛籃的次應力水平進行了參數分析。陳紹蕃則對桁架結構的次應力進行了系統的理論分析。

1 節點偏心的來源

在理想桁架中，其腹桿在節點處的交點與桁架弦桿中線相重合。在實際工程中，桁架的桿件尺寸布置受到橋梁縱坡，腹桿傾角以及桿件截面尺寸等多方面的影響，其腹桿中線在節點附近的交匯點很難與桁架腹桿的中線相重合，同時實際工程中的桁架桿件交匯處的節點通常使用焊接及螺栓連接等方式，節點剛性也使得節點偏心所引起的桿件彎矩無法得到釋放。這樣由于桁架節點剛性以及節點偏心共同引起的桿件彎矩稱之為次內力，其對桁架節點和桿件的受力狀態均較為不利。同時對于在公路桁梁橋中的鋼管桁架組合梁，通常還會將橋面板與桁架結構通過設置剪力連接件等方式相互連接，形成整體共同受力。而形成組合作用后的橋面板與弦桿形成整體，其截面中性軸的位置發生了改變，因此即使無節點偏心的桁架與橋面板所形成的組合梁，也應對其節點偏心的影響進行分析。因此本文著重對無偏心的理想鋼管桁架，有偏心的鋼管桁架以及有偏心的鋼管組合桁梁三種結構的次應力進行對比分析。

節點偏心分為三種，分別為節點正偏心、節點負偏心和無偏心。不同的節點偏心對結構的受力影響可能不同，相同的節點偏心對不同結構的受力影響也不同。

2 有限元模型算例

2.1 桁架尺寸

通過建立存在不同類型節點偏心的桁架及組合桁梁的有限元模型來對桁架次應力進行分析。為對桁架次應力進行有限元分析，根據相關工程經驗，初擬了一榀用于算例分析的簡支鋼管桁架。鋼桁架跨徑為32 m，桁高2.15 m，高跨比為1/14.9。腹桿采用三角形的Warren桁架布置，腹桿傾角為60°。桁架弦桿采用矩形鋼管，截面尺寸為300 mm×300 mm×16 mm，腹桿同樣采用矩形鋼管，截面尺寸為200 mm×300 mm×12 mm。混凝土組合桁梁的橋面板尺寸為2 500 mm×400 mm。

2.2 有限元模型

本文采用Midas Civil分別建立了3個有限元模型，其中模型1為無節點偏心的鋼管桁架模型，模型2為桁架下弦節點存在節點偏心的桁架模型，模型3為帶橋面板的桁架組合梁。

模型1～3中鋼材等級為Q345，混凝土標號為C40。模型1～3鋼管桁架均采用梁單元建立。桁架桁架弦桿與腹桿之間的連接采用共節點剛性連接，即模型考慮了節點剛性對桁架次應力的影響。模型1為存在節點偏心的桁架，其在下弦桿節點引入了節點偏心距如圖1(a)所示。同一節點的兩個腹桿與分別與下弦桿弦桿上不同的節點相連接，這兩個節點間距200 mm。；模型2、3均為無偏心桁架節點，其同一節點的兩個腹桿均與下弦桿同一節點相連接。鋼管桁架模型3中的混凝土橋面板與鋼管桁架上弦桿同樣采用雙單元共節點的方式連接，忽略可能存在的板桁界面滑移現象，同時對混凝土橋面板給與其一定的截面偏心，使得其底面與桁架上弦桿的頂面在同一水平面上。桁架下弦桿兩端采用簡支的邊界條件進行約束。模型1～3均進行了兩個施工工況的加載，工況1為跨中集中加載的荷載工況，集中荷載大小為200 kN，工況2而則為所有桁架上弦節點均施加相同的節點荷載的均布加載工況，均布荷載大小為40 kN·m。最終建立的有限元模型如圖1所示。

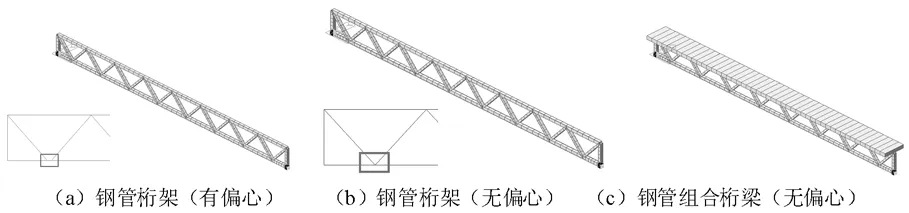
圖1 Midas有限元模型

3 結果討論

根據本文建立的Midas模型，對其進行有限元分析，最終得到了不同構造下的桁架在2個不同工況下的有限元計算結果。根據上一節對有限元模型的介紹可得，桁架的偏心節點均設置在弦桿，故本文以跨中下弦桿為例，提取跨中下弦桿桿件的軸力引起的應力與組合應力的比值k(軸向應力/正應力)作為表征桁架次應力水平的指標，并進行橫向對比，結果如圖2所示。易知軸向應力與正應力的比值k越大，說明桿件內力中軸力所占比例越大，桿件的次應力水平就越低，桁架的受力狀態就越為合理。

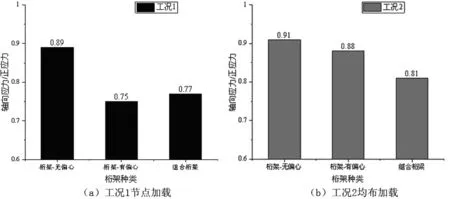
圖2 有限元分析結果

由圖5可得桁架節點偏心與桁架設置橋面板均可對桁架桿件的次應力產生影響。對于即使是不存在節點偏心的桁架，由于節點剛性等原因，其軸向應力和正應力比值k在0.9左右，且其受加載模式的影響較小。而對于存在節點偏心的桁架，其桿件的次正應力比顯著低于無偏心的桁架，并且其還會受到桁架加載模型的影響，軸向應力和正應力比值k在2個加載工況下分別為0.75和0.88，說明其在跨中節點加載時次應力的影響更大。對于設置了橋面板的組合桁梁來說，盡管橋面板設置在了桁架上弦平面，但其依然對下弦桿的次應力水平存在較為明顯的影響。在2個加載工況下的跨中軸向應力和正應力比值k分貝為0.77和0.81。因此對于設置了混凝土橋面板的鋼管組合桁梁，其次應力水平也不可忽略，應對其板桁組合效應所引起的次應力進行慎重的考慮。并且由本文的算例可以發現，桁架設置橋面板形成組合桁梁對次應力的影響甚至可能還要高于桁架節點偏心對次應力的影響。

4 結 論

本文首先對應用于實際工程的鋼管桁架次應力的來源進行了分析，進而通過建立有限元模型的方式對三種不同類型的鋼管桁架及組合桁梁的次應力水平進行了有限元分析，最終得到如下結論：節點偏心和設置混凝土橋面板均可對鋼管桁架的次應力造成影響；桁架節點偏心對次應力的影響還會受到加載模式的影響；當組合桁梁橋面板尺寸較大時，其對桁架次應力的影響大于節點偏心對次應力的影響。