水平圓柱體上波流力特征的數值模擬

王 艷，王樹齊，王坤鵬

(江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江 212003)

0 引 言

水平圓柱在復合式浮式防波堤中是一種常見的結構，海域中結構物所受的外力作用很多，波與流是其中的2種。由于波流的長期作用，結構物容易產生疲勞與坍塌，所以研究波流與結構物的作用對結構物設計和生產安全有著重要的現實意義。

早期針對波浪對非完全水平淹沒圓柱體已經有了大量的研究，其中大部分采用了理論分析和物理實驗的方法。Dixon等[1]考慮圓柱軸心和低于靜水面的情況，改變波浪頻率和圓柱的淹沒深度對水平圓柱體上的波浪力進行實驗研究。隨著流體計算的發展，對部分淹沒水平圓柱體上波浪力的數值模擬研究也不斷開展。Westpahlen等[2]采用有限體積法等CFD方法對波浪與非淹沒水平圓柱的作用問題進行數值模擬，計算水平圓柱所受的垂向力，發現計算結果與Dixon的實驗結果較為接近。Hu等[3]基于黏性流理論建立了數值波浪水槽，在線性波作用下對半淹沒水平圓柱體進行受力計算，其數值結果與Dixon的實驗值和Westpahlen計算值能夠較好吻合。劉必勁等[4]改進Morison方程對水平圓柱浮子所受波浪力進行準確預測，研究得出淹沒深度對圓柱體所受波浪力有影響。毛鴻飛等[5]改變部分淹沒水平圓柱體的垂向位置與波浪幅值，得出水平圓柱體所受波浪力隨著垂向位置升高而增大。

相對于波，波流對水平圓柱體的研究較少。Xiao等[6]研究了波流作用下圓柱體的受力情況，發現圓柱體所受的波流力大于波浪力與流體力的簡單求和。胡克等[7]研究波流作用下的水動力特性，得出流速與浸沒深度的增加能夠同時增加附加水質量系數和拖曳力系數。柏君勵等[8]研究波流與不同淹沒深度下的水平圓柱的影響時發現，波浪反射與阻塞作用共同影響水平圓柱所受波流力的大小。Bai等[9]通過修正Morsion方程與實驗值比較發現，在部分淹沒的情況下，測得值比理論值大，相反，在完全淹沒的情況下，測得值相對較低。

在此基礎上，本文對不同波幅、周期與圓柱淹沒深度對波流力特征的影響進行數值計算。基于STARCCM+軟件建立數值模型，采用的基本方程為Navier-Stokes（N-S）方程，數值離散方法為Finite Volume Method（FVM），湍流模型為Renormalizationgroup（RNG）k-w模型，捕捉自由表面用Volume of Fluid（VOF）方法，造波使用Fenton[10]的五階波浪理論，采用速度邊界法造波及阻尼消波。使用該模型，首先對半淹沒水平圓柱體的波流力進行數值驗證，驗證該模型對結構物受力的準確性。然后應用該模型對不同工況下的水平圓柱體進行波流力的數值計算，分析波幅、淹沒深度和波周期對水平圓柱體波流力的影響以及波流與圓柱相互作用時波浪的反射情況，為在波流作用下的結構物設計提供參考。

1 數值模型

1.1 控制方程

對于不可壓縮的黏性流體流動問題，可分別用如下張量形式表示連續方程和動量守恒方程：

式中： μi， μj為流體質點速度在i，j方向上的分量；t為時間；p為流體壓強； ρ 為流體密度； μ 為流體黏性系數；g為重力加速度。

1.2 自由液面處理方法

用VOF方法對數值模型的自由表面進行捕捉。α為每個計算單元的體積分數，其表示為：

混合流體的密度和黏性系數計算式為：

其中，下標w表示液相，a表示氣相。

1.3 邊界條件

數值波浪水槽模型及其平面圖如圖1所示。在水槽入口處給定邊界條件為速度入口，即造波采用的方法速度邊界法；頂部邊界只允許空氣離開或進入區域，因此給定壓力出口邊界；出口處采用阻尼消波，并給定壓力出口的邊界條件。水槽的底部邊界為不可滑移的固定邊界。其中造波區設置在水槽前端，其目的是協助生成波浪和吸收反射波浪；消波區設置在水槽末端，其功能是把出口邊界的波浪反射消除。

圖1 數值波浪水槽的示意圖Fig.1 Sketch of numerical wave flume

1.4 流體作用力

用下列方程計算結構物上的流體作用力：

式中：Fp和Fv分別是壓力和黏性切力；n為單為法向量；s單位切向量； τ為作用在物體上的剪切力。

2 數值驗證

參照Bai等[9]的物理實驗值，驗證半淹沒水平圓柱體上所受的流體作用力，計算設置如圖2所示。水平圓柱淹沒在水中一半，圓柱直徑D=0.06m，水深d=1.6m，流速c=0.2m/s，為了減少計算的工作量，造波理論采用了Fenton[10]提出的Stokes五階波理論，入射波周期T=0.7s，波高H=0.03m。

圖2 數值水槽模擬的示意圖Fig.2 The computation domain of water channel

將圓柱所受作用力的數值結果選取其中幾個周期與實驗結果作比較，如圖3所示。本文所有的受力數據均采用圓柱完全淹沒時的浮力進行無量綱處理，其中垂直作用力Fz為扣除初始時刻靜浮力后的值，如下式：

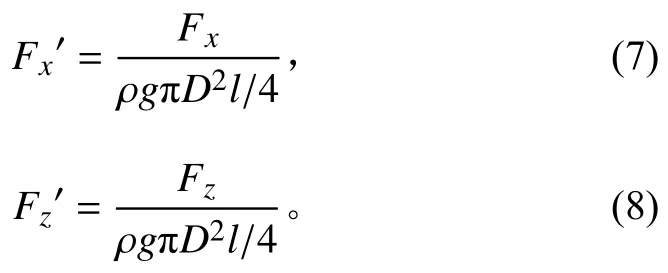
圖3 水平圓柱上的波流力Fig.3 Wave-current forces on a horizontal cylinder

通過觀察發現與已有文獻的實驗數據吻合良好，證明該模型非完全淹沒水平圓柱體所受波流作用力計算有著良好的計算精度。本文的流體力在波浪循環初期，升沉力占主導地位。在通過峰值后，力在減小，并在相對波周期的一半后變為負值。當波流進一步傳播，水位上升時，向下的力減小。

3 數值計算與結果分析

3.1 算例設置和計算參數

數值計算中，圓柱體的水平位置及造波區及工作區長度與驗證的算例相同，其中水深d=1 m，圓柱半徑r=0.05 m以及流速c=0.25 m/s保持不變。選取多個波高A=0.012 5～0.05m，取值間隔為0.012 5 m；多個垂向位置為0～0.1 m，取值間隔為0.025 m，其中垂向位置的距離是圓心與靜水面的距離值S；選取多個周期T=0.69 s，0.99 s，1.29 s，1.59 s。

3.2 網格收斂性驗證

選取3種不同的網格驗證網格的收斂性，分別對3種水平圓柱上所受的波浪力進行計算，網格參數如表1所示。計算參數為r=0.05 m，S=0 m，T=1.29 s。

表1 網格參數Tab.1 Mesh parameters

對比不同網格劃分下的圓柱所受的波流力，如圖4所示。由圖可見，網格2與網格3對應的數值尤為接近，而較稀疏的網格1與較密的網格相比較有些誤差。綜合以上3種網格，網格2是既符合精度要求又符合減少計算量的要求，因此后文以網格2的設置條件開展計算。

圖4 不同網格下的圓柱水平波流力時間歷程Fig.4 Time-series of horizontal wave-current forces on a cylinderwith different mesh

3.3 數值結果與分析

對不同的波幅、淹沒深度及周期下的波流作用力進行計算并在圓柱上游2D和下游2D處監測波高，分析波幅等對波反射與波阻塞的影響。

3.3.1 波流與水平圓柱體相互作用時的自由表面變形

圖5為S=0 m，T=1.29 s下幾個不同波幅工況的時歷曲線，此時圓柱圓心在水平面上。從圓柱上游2D和下游2D處的波高歷時曲線對比發現，在波流情況下，圓柱處于部分淹沒時會形成顯著的波反射和波浪阻塞，隨著波幅的增大，波浪反射與波浪阻塞明顯增加。在圓柱處于半淹沒時波浪反射比波浪阻塞的作用要大。

圖5 不同波幅下圓柱上游2D與下游2D的時間歷時曲線Fig.5 Time-series curves of 2D upstream and 2D downstream of cylinder under different wave amplitudes

圖6為A=0.05 m，T=1.29 s下幾個不同深度工況的時歷曲線。對比圓柱上游2D和下游2D處的波高歷時曲線發現，隨著淹沒深度的增加，波浪反射在減小，波浪阻塞在增加，波浪阻塞漸漸大于波浪反射的作用。

圖6 不同深度下圓柱上游2D與下游2D的時間歷時曲線Fig.6 Time-series curves of 2D upstream and 2D downstream of cylinder under different wave amplitudes

對圖5各波高曲線進行傅里葉變換，如圖7所示。和圖5類似，當圓柱部分淹沒流速不變時，上游2D處會形成明顯的反射波，并與入射波疊加使得圓柱上游的水面振幅顯著上升，并隨著波幅的增大，波反射越明顯。在下游2D處會形成明顯的波阻塞效應，隨著波幅的增大，波阻塞越明顯。與圖5對比來看，圓柱對波的反射作用比阻塞作用明顯更大，此時波浪反射作用占主導。此外，還可以看出，在半淹沒狀態下，此時波流與圓柱相互作用時，波浪的高階成分非常多，自由液面的非線性很大。

圖7 不同波幅下圓柱上游2D與下游2D處自由液面的傅里葉譜對比Fig.7 Comparison of Fourier spectra of free surface at 2D upstream and 2D downstream of cylinder under different wave amplitudes

對圖6各波高曲線進行傅里葉分析，如圖8所示。和圖6類似，隨著淹沒水深的增加，波浪阻塞在增加，波浪反射在全部淹沒時減小，波浪阻塞漸漸占主導作用。

圖8 不同垂向位置下圓柱上游2D與下游2D處自由液面的傅里葉譜對比Fig.8 Comparison of Fourier spectrum of free surface at 2D upstream and 2D downstream of cylinder at different vertical positions

3.3.2 波流對水平圓柱的作用力分析

圖9為工況T=1.29 s，S=0 m下，幾個不同波幅下的圓柱所受波流水平作用力與垂向作用力的時間歷程結果。圖10為工況T=1.29 s，S=0 m，A=0.05 m下的渦量圖。由圖9可知，波幅較小的情況下，作用力曲線比較平滑；隨著波幅的增大，流體力曲線變得粗糙。這是由于波幅的增大，波浪能夠逐步爬高到圓柱最高點。隨著波幅增大，圓柱所受的波流作用力也隨之增大。水平作用力的正值隨著波幅的增加，變化幅度逐漸減少，垂向力的正向幅值變化也逐漸減小；圓柱所受力的不對稱越發明顯，且水平力的正方向數值逐漸大于負方向，垂向力的負方向數值逐漸大于正方向，這是由于隨著波幅的增加，波浪反射在增加，圓柱上游振幅增加使得垂直于波向的投影面積與排開水的體積增大。由圖10可知，在部分浸沒的情況下，波流與圓柱的作用時，圓柱迎浪面的液面先升高，進而帶動背浪面水深增高，波流力為正。經過一段時間后，圓柱迎浪面水體下降，這時背浪面高于迎浪面，此時水平波流力方向與之前相反。

圖9 波流力時間歷程Fig.9 Time-series of wave-current force

圖10 波流下的渦量場分布圖Fig.10 Distribution of vorticity field under wave-current

不同的S/D下正向水平力和垂向波流力隨A/r的變化特征如圖11所示。隨著波幅的增加，波流力在總體上呈現上升的趨勢。隨著淹沒深度的增加，波流力呈現出不同的發展趨勢。在部分浸沒時，隨著深度的增加，正向水平力呈現上升的趨勢，正向垂向力隨著波幅的增加呈現著下降的趨勢。隨著波幅和垂向位置的增加，圓柱對波流的反射作用越強，使得上游的振幅增加，疊加波波峰越高波谷越低，所以圓柱的受力峰值在增加。在完全浸沒時，正水平力隨著浸沒深度增加而呈現下降趨勢，正向垂向力隨著浸沒深度的增加而上升，此外在剛好完全淹沒的時候，正垂向力沒有正值。這是由于當圓柱處于完全淹沒時，波反射作用迅速減小。隨著淹沒深度的增加，浮力的影響較小，但隨著波幅和水深的增加，波流的阻塞作用越強。當圓柱處于S/D=0.5時，圓柱頂部與自由液面剛好相切，此時的波浪反射很大，大于阻塞作用，類似前面分析。此時圓柱的受力峰值在增加，所以正水平力很大，又由于完全淹沒，使得浮力對垂向力的影響小，所以垂向力很小。

圖11 不同S/D下正向波流力隨A/r的變化對比Fig.11 Comparison of forward wave-current force withA/r under differentS/D

不同的S/D下負向水平和垂向波流力隨A/r變化特征如圖12所示。垂向力（負的極值以絕對值比大小）在部分淹沒的情況下，隨著淹沒深度與波幅的增加，負水平力與垂向力的大小在增加；隨著波幅的增加，不同深度下的水平力與垂向力的大小趨于一個值。在圖11全部浸沒的情況下，隨著淹沒深度的增加，負水平力的大小隨之減小，負垂向力也隨之減小。這是由于全部淹沒時，波浪阻塞大于波浪反射，波浪阻塞降低了圓柱周圍水的速度和加速度，從而減小了圓柱所受的波流力。

圖12 不同S/D下負波流力隨A/r的變化對比Fig.12 Comparison of negative wave-current force withA /r under differentS/D

圖13為S=0 m時不同波幅下的正向波流力隨著頻率的變化特征。隨著頻率和波幅的增大，水平波流力也隨之增大；垂向波浪力的變化在頻率較小時，變化幅度稍微大一些，隨著頻率的增加，垂向波流力的大小趨于平緩，接近一個特定值，并隨著波幅的增大，這一值也隨之增大。

圖13 不同A/r下正向波流力隨頻率的變化對比Fig.13 Comparison of forward wave-current force with frequencies at differentA/r

4 結 語

本文對水平圓柱體在波流下所受的力開展數值模擬。首先用前人的實驗數據驗證數學模型的有效性，其次對不同工況下的波流力進行分析，如下：

1）在水平圓柱體部分淹沒時，隨著波幅的增加，波浪的反射與阻塞作用都在增加，但波浪反射大于阻塞作用；圓柱在完全淹沒時，隨著淹沒深度的增加，波浪反射作用減小，阻塞作用增大且大于反射作用，所以波幅與垂向位置對于圓柱所受波流力的研究有著極大的影響。

2）水平圓柱所受的波流力隨波幅的增大而增大，在部分浸沒時，波流力隨著波幅的增大，正負方向的力開始變得不對稱起來，水平力正方向的大小逐漸大于負方向，負垂向力的大小逐漸大于正垂向力的數值，這主要受波浪反射和阻塞的影響。

3）隨著波幅與垂向位置的改變，圓柱所受的波流力也呈現了一些規律。在部分淹沒的情況下，隨著波幅的增加和垂向位置的增加，水平波流力的大小在增加，垂向波流力的大小在減小；在完全淹沒的情況下，水平波流力的大小在減小，正垂向波流力在增加，負垂向波流力的大小在減小，這是波浪的反射與阻塞共同作用下的結果。

4）在部分浸沒下，隨著頻率的增加，水平圓柱所受的波流正向垂向力趨于平緩接近一個特定值。