一階線性變系數(shù)對(duì)流方程的穩(wěn)定性分析
張?zhí)鹛穑S文文,郭紅,杜明洋,余昌彪
(齊魯工業(yè)大學(xué)(山東省科學(xué)院) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,山東 濟(jì)南 250301)
變系數(shù)對(duì)流擴(kuò)散方程對(duì)研究自然界和實(shí)際工程中的很多物理現(xiàn)象具有重要意義,且在眾多學(xué)科中的應(yīng)用極其廣泛,如流體力學(xué)、氣體力學(xué)等[1-2]。在研究此類問(wèn)題時(shí),擴(kuò)散項(xiàng)的計(jì)算相對(duì)簡(jiǎn)單,對(duì)流方程的計(jì)算通常是研究重點(diǎn)。
一階變系數(shù)對(duì)流方程在自然科學(xué)領(lǐng)域的應(yīng)用背景較廣泛。王國(guó)棟等[3]將迎風(fēng)格式應(yīng)用到一階變系數(shù)對(duì)流方程的推廣模型交通流中,并通過(guò)新的格式模擬相關(guān)實(shí)例;Chen 等[4]通過(guò)耗散譜方法求解一階變系數(shù)雙曲方程(對(duì)流方程是最簡(jiǎn)單的雙曲方程),通過(guò)傅里葉耗散譜方法討論周期問(wèn)題,通過(guò)Legendre耗散譜方法討論邊界問(wèn)題,且列出嚴(yán)格的誤差估計(jì)式; Aguirre等[5]在以Hermit函數(shù)為正交基的Herbert空間里開展對(duì)一階變系數(shù)雙曲方程周期邊界問(wèn)題的研究,通過(guò)理論分析給出了收斂階 。關(guān)于對(duì)流方程的傳統(tǒng)數(shù)值解差分格式有迎風(fēng)格式、Lax-Friedrichs格式、Lax-Wendroff格式、Beam-Warming格式和蛙跳格式。其中,迎風(fēng)格式的基本思想是用向前差商或向后差商來(lái)代替空間偏導(dǎo)數(shù),其關(guān)于時(shí)間和空間都是一階的,且是條件穩(wěn)定的,算法在計(jì)算機(jī)上便于實(shí)現(xiàn),因此在實(shí)際計(jì)算中受到廣泛重視,并得到了一些好的方法和技巧。本文我們將采用迎風(fēng)格式逼近一階變系數(shù)對(duì)流方程并探索格式的穩(wěn)定性條件[6-9]。
常系數(shù)問(wèn)題差分格式的穩(wěn)定性分析一般采用傅里葉方法和直接方法[9-11],但是變系數(shù)問(wèn)題的穩(wěn)定性分析相對(duì)復(fù)雜,通常不采用上述兩種方法,目前國(guó)內(nèi)外關(guān)于一階變系數(shù)對(duì)流方程穩(wěn)定性的相關(guān)研究較少。對(duì)于變系數(shù)方程差分格式穩(wěn)定性問(wèn)題,能量不等式方法是一個(gè)嚴(yán)格且很有技巧的方法。用能量不等式方法討論差分格式穩(wěn)定性是從穩(wěn)定性的定義出發(fā),通過(guò)一系列估計(jì)式完成的,這個(gè)方法是偏微分方程中常用的能量方法的離散模擬[9]。本文將采用能量不等式方法分析一階變系數(shù)對(duì)流方程迎風(fēng)格式的穩(wěn)定性條件,分別就變系數(shù)的正負(fù)取值情況并結(jié)合凍結(jié)系數(shù)法驗(yàn)證網(wǎng)格比條件,進(jìn)而推導(dǎo)出穩(wěn)定性條件,最后進(jìn)行數(shù)值模擬驗(yàn)證理論分析的正確性。
1 一階線性變系數(shù)對(duì)流方程初值問(wèn)題
對(duì)于簡(jiǎn)單的一階線性變系數(shù)對(duì)流方程的初值問(wèn)題:
(1.1)
如果a(x,t)對(duì)x和t都是一次連續(xù)可微的,那么a(x,t)光滑變化,與常系數(shù)情形類似,(1.1)式的特征線滿足的方程為:
(1.2)
令x=x(t,x0)和u(x,t)分別是方程(1.1)和方程(1.2)的解,則:
(1.3)
于是,方程(1.1)的解沿特征線為常數(shù)。此時(shí)特征線為曲線,且有:
u(x,t)=u0(x),x=x(t,x0)。
(1.4)
因此,我們將已學(xué)常系數(shù)方程推導(dǎo)的差分格式推廣到變系數(shù)方程(1.1)。
2 迎風(fēng)格式
設(shè)初值問(wèn)題(1.1)的解區(qū)域?yàn)閇0,l]×[0,T],將此區(qū)域沿x軸和t軸方向進(jìn)行矩形網(wǎng)格剖分,其中空間步長(zhǎng)為Δx=h=l/J,時(shí)間步長(zhǎng)為Δt=τ,網(wǎng)格點(diǎn)記為(xj,tn),網(wǎng)格線可寫作:
xj=jΔx=jh,j=0,1,2,…,J,
tn=nΔt=nτ,n=0,1,2,…。
由于變系數(shù)對(duì)流方程(1.1)的迎風(fēng)差分格式是對(duì)流方程關(guān)于空間偏導(dǎo)數(shù)用在特征線方向一側(cè)的單邊差商來(lái)代替的,且其系數(shù)a(x,t)符號(hào)是變化的,因此迎風(fēng)格式可以寫成如下兩種形式:
(2.1)
(2.2)
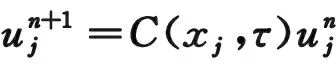
|λj(G(τ,k))|≤1+Mτ,j=1,2,…,p,
其中|λj(G(τ,k))|表示增廣矩陣G(τ,k)的特征值,M為常數(shù)[9]。此條件稱為von Neumann條件。
3 穩(wěn)定性分析
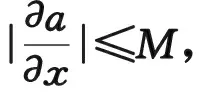
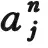

(3.1)
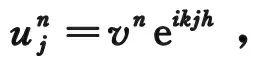
vn+1eikjh=vneikjh-aλ(vneikjh-vneik(j-1)h),
(3.2)
兩邊同時(shí)消去公因子eikjh得:
vn+1=vn[1-aλ(1-e-ikh)],
(3.3)
所以增長(zhǎng)因子為:
(3.4)
則有
|G(τ,k)|2=[1-aλ(1-coskh)]2+a2λ2sin2kh
(3.5)
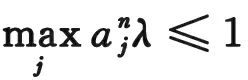
接下來(lái)我們分情況討論迎風(fēng)格式穩(wěn)定性:

(3.6)
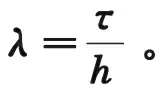
(3.7)
網(wǎng)格比滿足條件:
(3.8)
根據(jù)基本不等式a2+b2≥2ab并進(jìn)一步化簡(jiǎn)有:
用h乘上式兩邊并對(duì)j求和,記離散范數(shù):
(3.9)
那么有:
(3.10)
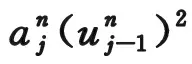
(3.11)
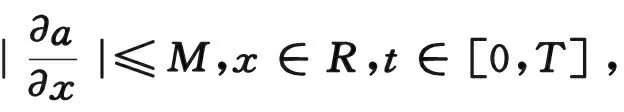
(3.12)
從而有
(3.13)
重復(fù)使用上式有:
(3.14)

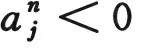
(3.15)
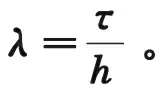
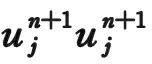
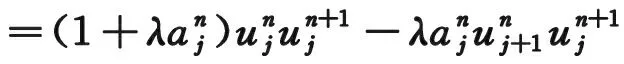
同理可知網(wǎng)格比滿足如下條件:
(3.16)
根據(jù)基本不等式a2+b2≥2ab并進(jìn)一步化簡(jiǎn)有:
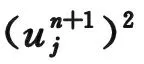
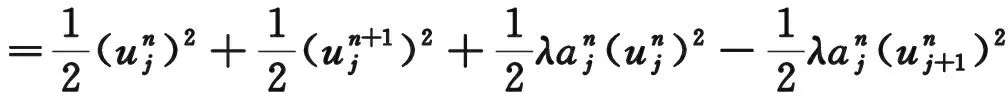
用h乘上式兩邊并對(duì)j求和,記離散范數(shù):
(3.17)
那么有:
(3.18)
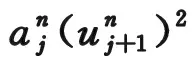
(3.19)
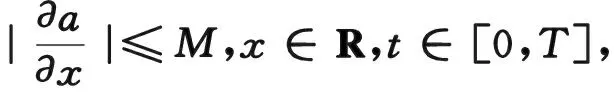
(3.20)
從而有
(3.21)
重復(fù)使用上式有:
(3.22)

4 數(shù)值算例
現(xiàn)在通過(guò)一個(gè)簡(jiǎn)單的數(shù)值例子驗(yàn)證用能量不等式的方法分析變系數(shù)對(duì)流方程的初值問(wèn)題的迎風(fēng)格式的穩(wěn)定性條件。
對(duì)于初值問(wèn)題:
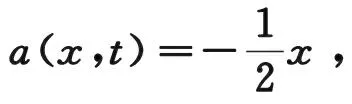
u(x,t)=x2et。
(4.1)
取空間步長(zhǎng)h=0.01, 時(shí)間步長(zhǎng)τ=0.01,則λ=1,將迎風(fēng)格式計(jì)算到tn=0.1時(shí),計(jì)算得到初值問(wèn)題的迎風(fēng)格式的數(shù)值解與解析解,然后將數(shù)值解與解析解進(jìn)行對(duì)比判斷此初值問(wèn)題的穩(wěn)定性,參考文獻(xiàn)[12],對(duì)隨機(jī)選取的部分輸出結(jié)果進(jìn)行對(duì)比,見表1。
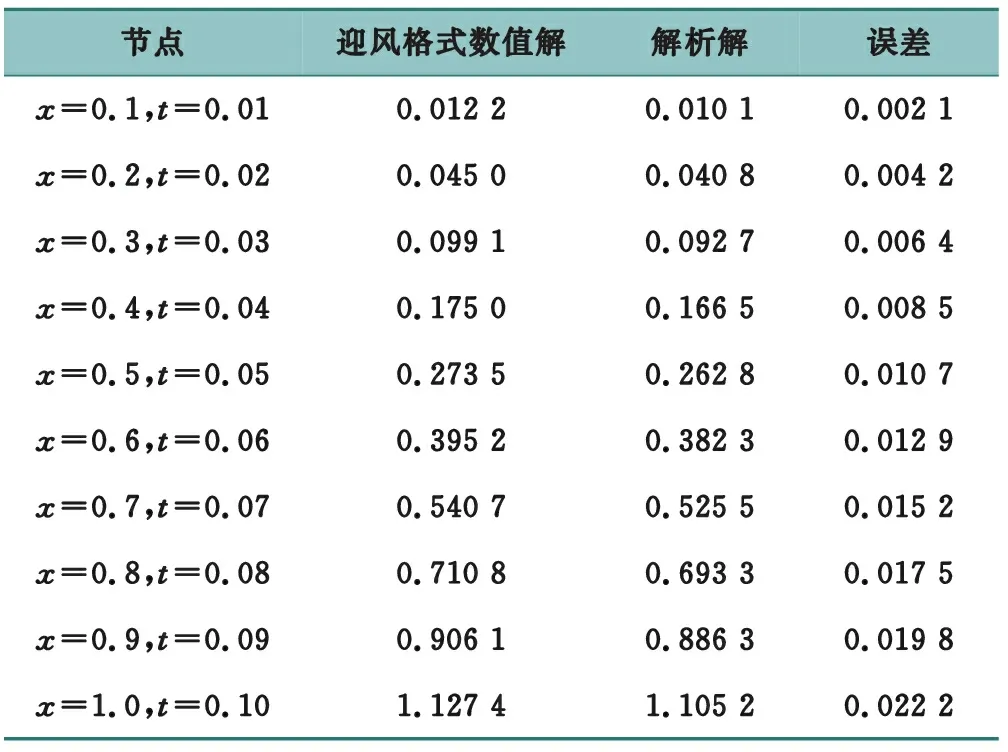
表1 數(shù)值解與解析解
從表中數(shù)據(jù)可知,迎風(fēng)格式的數(shù)值解與解析解的誤差很小,即可認(rèn)為此初值問(wèn)題是穩(wěn)定的。
圖1和圖2為輸出迎風(fēng)格式的數(shù)值解圖像與解析解圖像,x軸代表空間方向的長(zhǎng)度,y軸代表時(shí)間方向的長(zhǎng)度,圖1的z軸是所研究初值問(wèn)題的迎風(fēng)格式關(guān)于x軸和y軸的數(shù)值解u(x,t),圖2中的z軸是所研究初值問(wèn)題關(guān)于x軸和y軸的解析解z(x,t)。從迎風(fēng)格式的數(shù)值解與解析解圖像可以直觀地看出此初值問(wèn)題的迎風(fēng)格式是穩(wěn)定的。
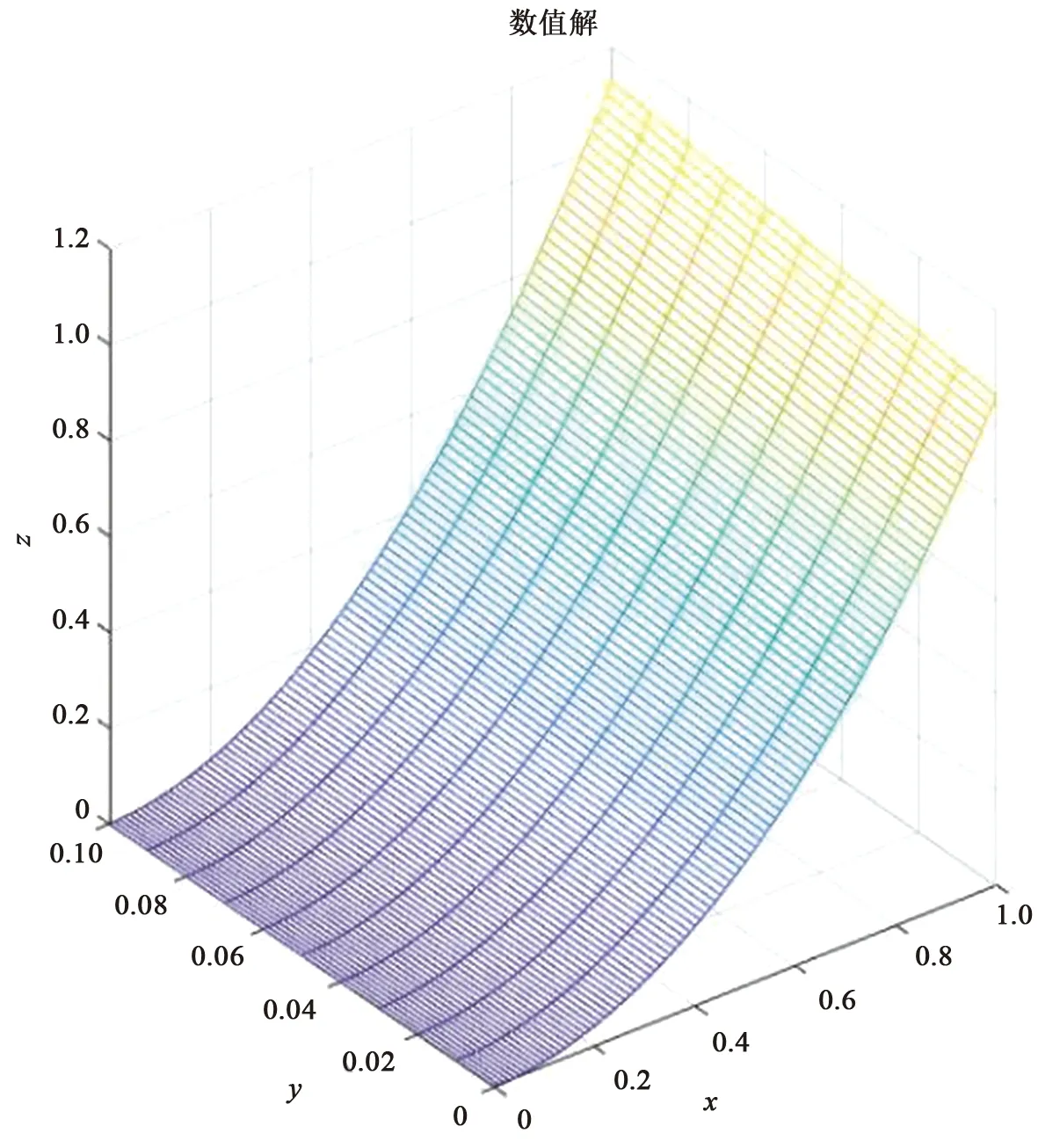
圖1 迎風(fēng)格式數(shù)值解Fig.1 Upwind scheme numerical solution
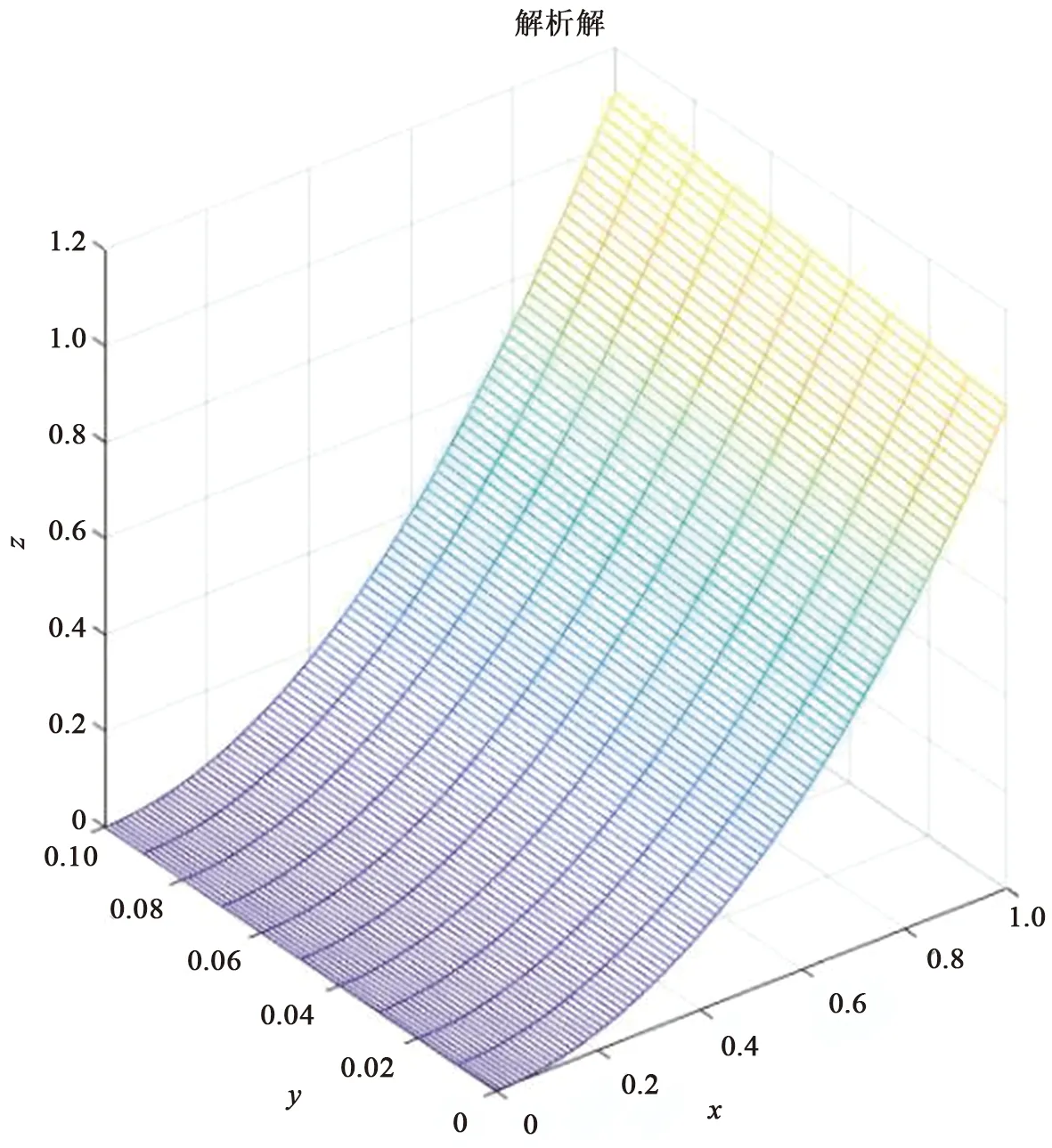
圖2 解析解Fig.2 Analytical solution
5 結(jié)語(yǔ)
本文采用迎風(fēng)格式逼近變系數(shù)對(duì)流方程,然后通過(guò)凍結(jié)系數(shù)法求出一階變系數(shù)對(duì)流方程的迎風(fēng)格式穩(wěn)定需要滿足的網(wǎng)格比條件。再對(duì)其迎風(fēng)差分格式通過(guò)能量不等式的方法并結(jié)合凍結(jié)系數(shù)法得出的網(wǎng)格比條件進(jìn)行討論得出其穩(wěn)定性條件。最后通過(guò)一個(gè)數(shù)值算例對(duì)比其解析解與數(shù)值解,驗(yàn)證穩(wěn)定性條件的正確性。

