基于電磁-熱耦合原理的三芯鎧裝電纜在低頻輸電方式下的損耗特性研究

劉士利 羅英楠 劉宗燁 鄧金鎖 蔡國偉

（1. 現代電力系統仿真控制與綠色電能新技術教育部重點實驗室（東北電力大學） 吉林 132012 2. 先進輸電技術國家重點實驗室（全球能源互聯網研究院有限公司） 北京 102209）

0 引言

隨著能源枯竭和環境污染問題越發嚴峻，目前全球海上風電開發呈現出深遠海化和集群化的發展趨勢[1]，離海岸距離超過100km 的深遠海域具有更豐富的風能資源，是未來海上風電探尋的重點方向[2]。德國等部分歐洲國家的深遠海風電場已經投運[3]，中國已經進行了基礎前瞻性探索[4-6]，其中，大規模風電跨海遠距離輸送是深遠海域風能開發涉及的關鍵問題之一。

海上風電輸送技術難度較大和成本較高，一般采用電纜線路。采用直流輸電方式雖然可以減小損耗提升載流量，但直流電壓下空間電荷積累效應給電纜絕緣帶來了嚴峻挑戰，在一定程度上限制了輸送容量的提升。若采用工頻交流輸電，則由電容效應導致的無功電流和電磁感應引起的護套感應電流將顯著影響電纜的輸送容量、傳輸距離和經濟性。而介于工頻和直流之間的低頻乃至分頻輸電方式可能在海上風電并網中得到廣泛應用[7-9]。因此電纜在低頻輸電方式下的損耗和載流特性是深遠海風電高效輸送的關鍵因素之一。

目前，關于電纜護套感應電壓、環流損耗的研究多集中于工頻輸電方式，采用的方法有IEC 標準法及有限元方法。文獻[10]分析了多回路電力電纜不同敷設方式對環流的影響，指出了不同相序組合下的環流分布規律；文獻[11]基于光電復合海纜的有限元模型，提出了光纖溫度變化模型；文獻[12]建立了光電復合海纜的熱路模型；文獻[13-15]采用有限元多物理場仿真方法，分析了不同敷設條件下海底電纜的溫度和載流特性；文獻[16]通過建立環形紋和螺紋護套的參數方程，提出了線芯與波紋護套的互感和等效直徑方法誤差的解析公式；文獻[17]采用有限元法研究了護套材料磁導率、體積電阻率對護套感應電壓的影響；文獻[18]基于電路模型推導了雙回路敷設電纜護套環流的計算方程，提出了減小護套環流的技術方案；部分學者還研究了電纜及周圍媒質的溫度場分布和熱特性[19-21]。而關于電纜在低頻輸電方式下的損耗和載流特性研究較少。文獻[22]基于系統技術經濟性，討論了分頻輸電方式下交流電纜載流量、傳輸極限等問題；文獻[23]研究了城市電纜線路在低頻輸電方式下的運行特性。綜上所述，關于三芯海底電纜在低頻輸電方式下的損耗特性，鮮有文獻報道。

本文采用有限元方法，建立了三芯鎧裝電纜的電磁-熱多物理場仿真模型，研究了其在低頻運行方式下的損耗和載流特性，分析了纜芯電流在低頻輸電方式下的不均勻分布特性，研究了輸電頻率、纜芯半徑等因素對護套感應電壓、損耗因子及載流量的影響，并分析了IEC 標準計算誤差，計算結果為提高深遠海電纜線路的經濟性提供了數據支撐。

1 三芯鎧裝電纜護套感應電壓解析計算

運行過程中電纜護套損耗由護套上的感應電壓和電流引起，因此在分析電纜護套損耗之前應首先明確護套感應電壓的計算。相較于單芯電纜，三芯鎧裝電纜能大幅度節省輸電走廊，提高傳輸容量，因此海上風電傳輸往往采用三芯光纖復合海底電纜，其結構示意圖如圖1 所示。

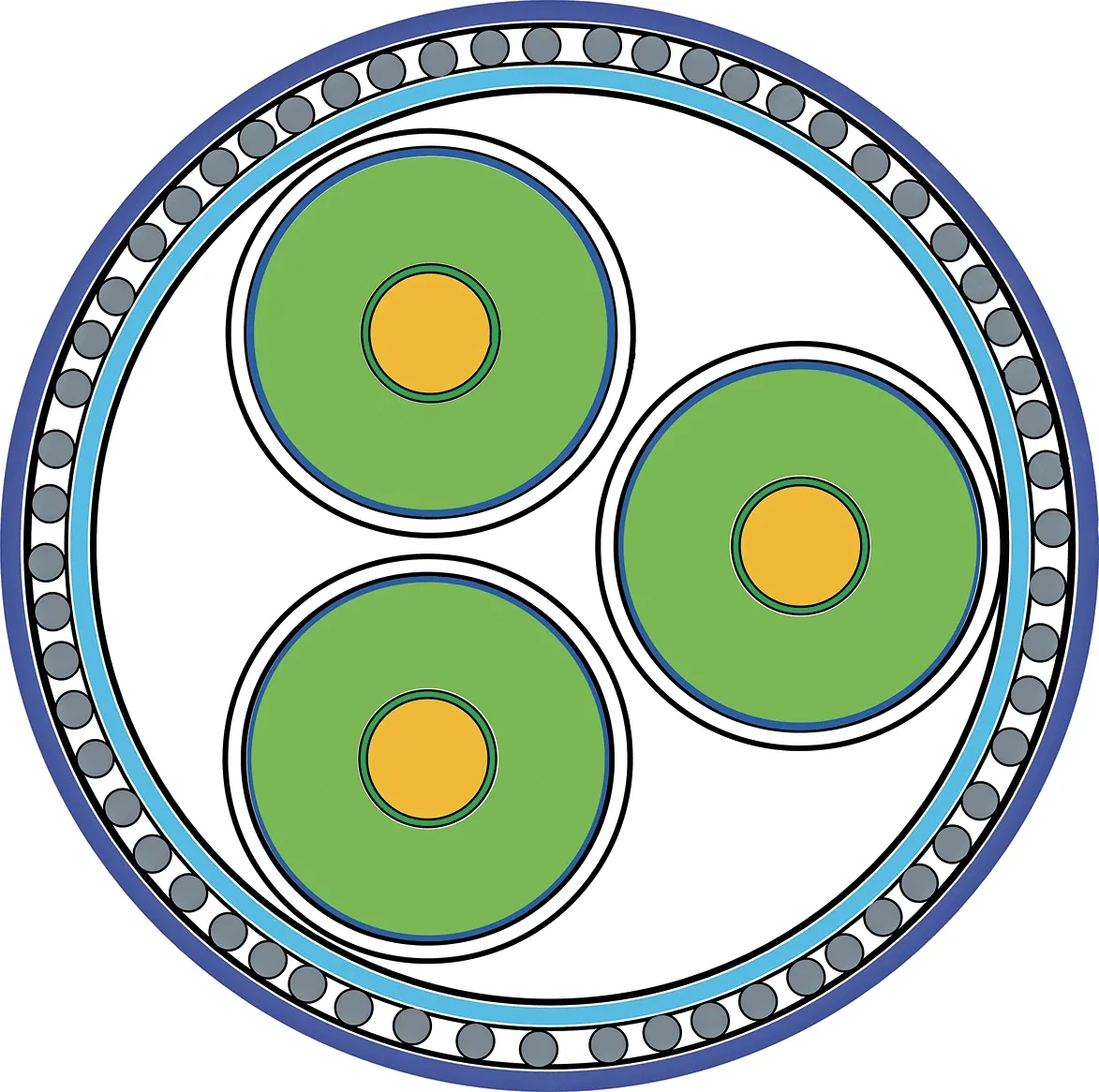
圖1 三芯鎧裝電纜結構示意圖Fig.1 Structure of three-core armored cable

根據電磁場理論，纜芯電流激發的交變磁場將在電纜護套和鎧裝中產生感應電壓，設三芯電纜流過三相平衡電流，其復數形式為

式中，I為三相電流有效值。

按IEC 標準，當導體P 和A、B、C 三相纜芯平行布置時，如圖2 所示，則三相電流產生的與P導體交鏈的磁通可表示為式中，RP為導體P 的幾何半徑；S1、S2、S3分別為三相纜芯與導體P 之間的距離。

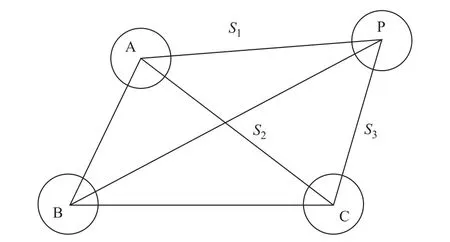
圖2 電纜護套感應電壓等效分析模型Fig.2 Equivalent analysis model for induced voltage of cable sheath

對于三芯鎧裝海底電纜，護套可視為上述導體P 的特例，其與纜芯的間距等于護套平均半徑，此時，護套感應電壓計算式為

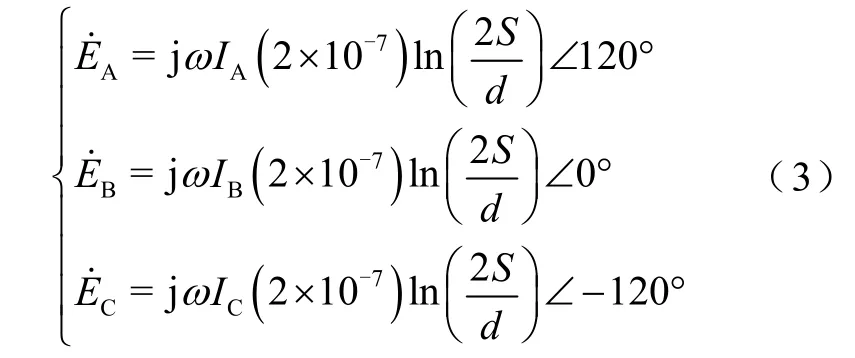
式中，d為護套直徑的幾何平均值；S為纜芯軸間距離。

上述護套感應電壓計算公式是基于電纜簡化模型推導得出，模型首先假設電流均勻分布，在處理某些環節時進一步假設電流集中于纜芯中央。而實際電流則由于趨膚效應和鄰近效應的影響，在纜芯中并非均勻分布；且隨著傳輸容量的上升，纜芯半徑越大、結構越復雜，電流不均勻分布越明顯，解析法計算就愈發困難。因此，對于三芯鎧裝海底電纜，采用上述解析公式進行計算，精度難以滿足要求，有必要建立精確的有限元場模型進行分析。

2 三芯電纜電磁特性有限元分析

2.1 電磁-熱耦合分析模型

電磁-熱多物理場耦合模型以電磁場的麥克斯韋方程組和熱傳導的傅里葉定律為基礎，電纜中電磁參數滿足

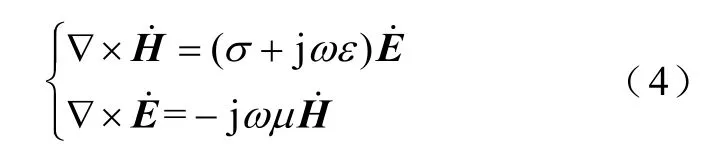
式中， ˙H為磁場強度矢量相量（A/m）； ˙E為電場強度矢量相量（V/m）；σ為電導率（S/m）；ω為角頻率（rad/s）；ε為介電常數（F/m）；μ為磁導率（H/m）。

引入相量形式的矢量磁位˙A，上述方程可以轉化為頻域下的二階偏微分方程，即

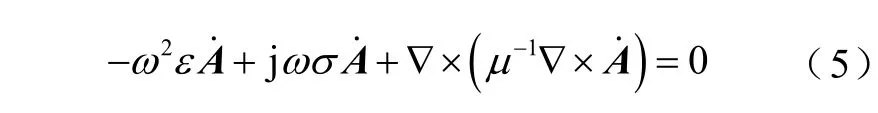
由上述方程得出矢量磁位˙A之后，可按式（6）求得磁感應強度。

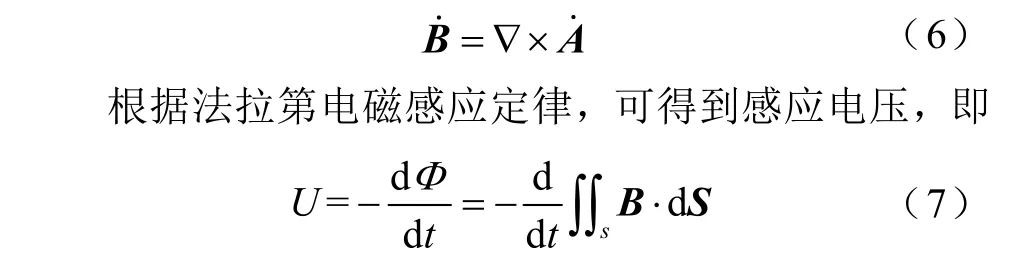
式中，Φ為與金屬護套交鏈的磁通。

電纜實際運行過程中，纜芯和金屬護套的電導率均受溫度影響，其與溫度的函數關系為

基于電磁場和溫度場雙向耦合的電纜損耗分析流程如圖3 所示。

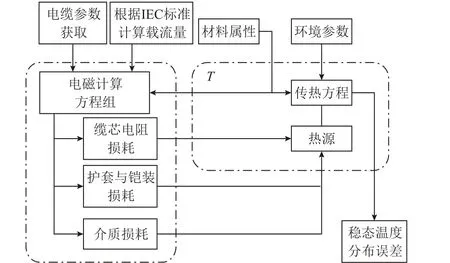
圖3 電磁-熱耦合分析原理Fig.3 Principle of electromagnetic-thermal coupling analysis

2.2 纜芯電流分布及護套感應電壓

三芯電纜的幾何尺寸見表1，敷設條件如圖4所示。通過電磁-熱多物理場仿真計算，三芯鎧裝電纜的磁場分布如圖5 所示。

圖4 電纜敷設條件Fig.4 Cable laying conditions

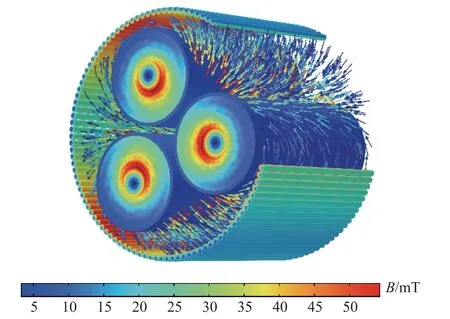
圖5 電纜磁場分布Fig.5 Magnetic field distribution of cable

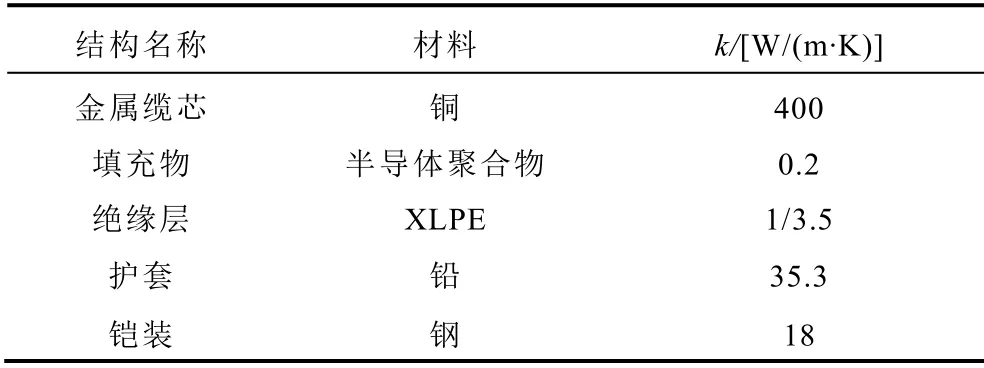
表1 電纜物理參數Tab.1 Cable physical parameters

當輸電頻率為50Hz 時，纜芯和護套中的電流分布如圖6 所示。可以看出，纜芯電流明顯呈不均勻分布，在三根纜芯相互靠近的一側電流密度較大，在遠離的一側較小。纜芯電流的不均勻分布由趨膚效應和鄰近效應引起。纜芯電流分布隨頻率的變化趨勢如圖7 所示。可以看出，頻率越高，電流不均勻度越明顯；且電流密度平均值位置和纜芯中心偏離較大，該偏離距離正是導致IEC 標準計算護套感應電壓存在誤差的原因之一。可以預見，電纜結構越復雜，其誤差越大。

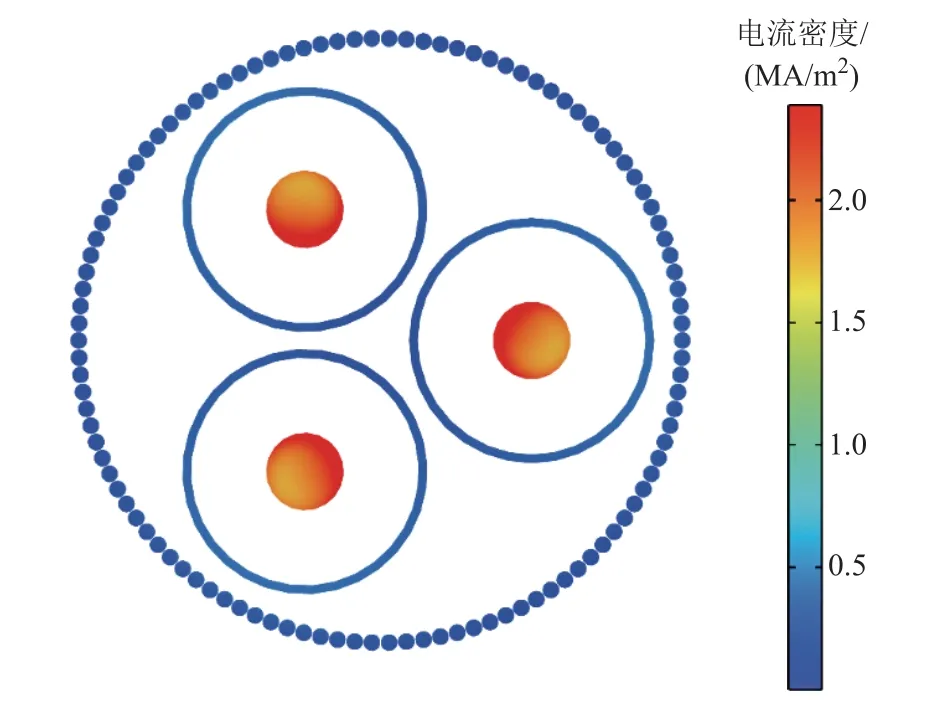
圖6 纜芯與護套的電流密度Fig.6 Current density of cable core and sheath

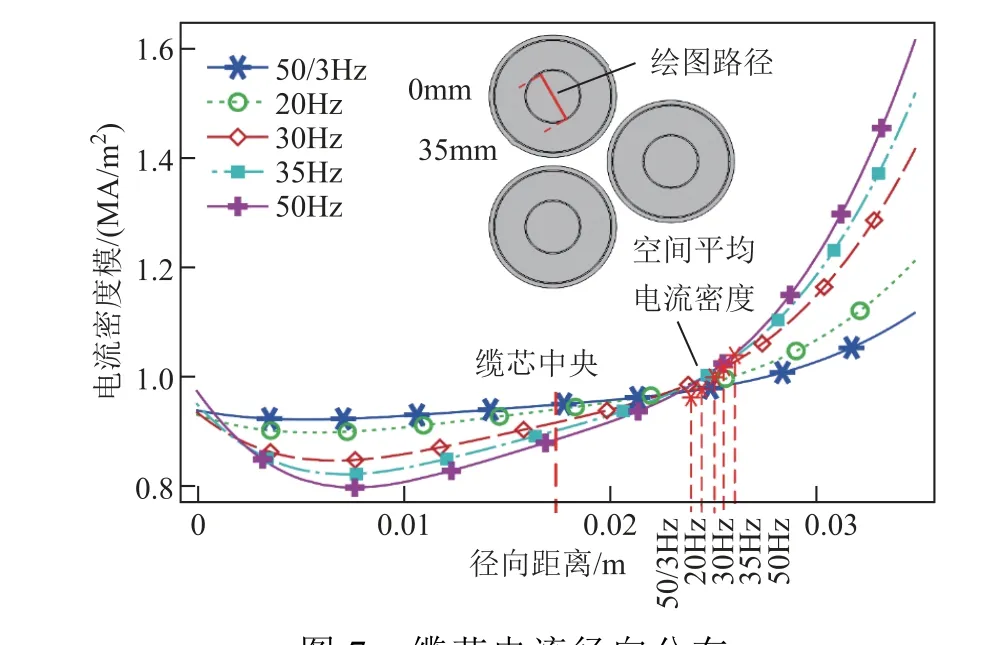
圖7 纜芯電流徑向分布Fig.7 Radial distribution of core current

不同頻率時，采用有限元法計算的護套感應電壓如圖8 所示，可以看出，采用電流均勻分布假設時，計算結果偏大，且隨著頻率增加，二者之間的偏差逐漸增大，分頻時誤差為8.4%，工頻時的誤差為13%。

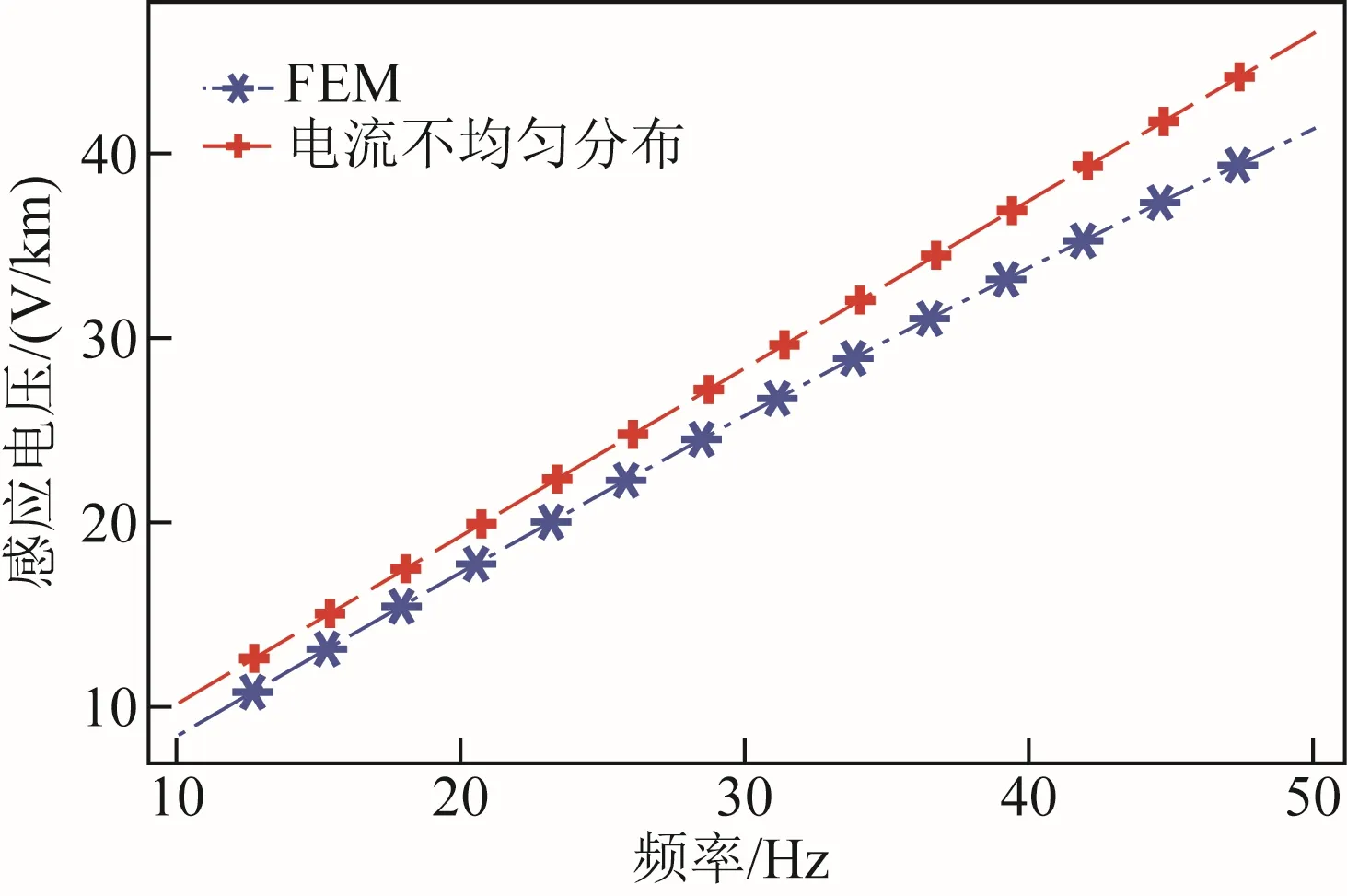
圖8 電纜護套感應電壓Fig.8 Induced voltage of cable sheath

2.3 護套損耗

電纜護套中的感應電流會產生額外的損耗，從而導致電纜溫度進一步上升，因此，準確計算護套損耗對于合理確定三芯海底電纜載流量，提升海上風電的經濟性具有重要意義。根據IEC 標準，在不考慮鎧裝的情況下，護套中的總損耗由環流損耗和渦流損耗構成，損耗因子可表示為

式中，X為電纜護套電抗（Ω/m）；Rs為護套電阻（Ω/m）；R為纜芯電阻（Ω/m）；S為三相導體間的纜芯軸間距離(m)。

式中，ts為護套厚度（mm）；Ds為電纜護套的外徑（mm）；ρ0為護套材料的電阻率（Ω·m）。

上述公式在計算λ1時沒有考慮鄰近效應，這同樣導致公式在計算三芯海底電纜損耗因子時精度降低。輸電頻率一方面影響纜芯電流分布、纜芯電阻及纜芯歐姆損耗，另一方面還影響護套感應電壓及護套損耗，而IEC 標準在計算λ1過程中做出的某些假設并未計及上述影響。此外，若考慮鎧裝，1λ′可由式（14）給出，此時電纜結構更加復雜，IEC 標準的計算誤差會更大。因此，需要構建有限元模型進行詳細討論。

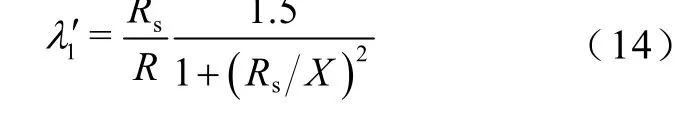
采用有限元分析可以得出，輸電頻率及纜芯半徑對纜芯電阻的影響如圖9 所示，可以看出，由于趨膚效應和鄰近效應的存在，隨著頻率的增加，電阻明顯增加，從而將導致纜芯損耗增加。

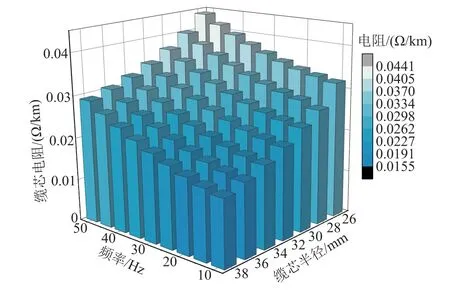
圖9 輸電頻率及纜芯半徑對電阻的影響Fig.9 Influence of transmission frequency and core radius on resistance

輸電頻率對損耗因子的影響如圖10 所示，可以看出，采用有限元計算時，如采用電流均勻分布模型，其計算結果和IEC 標準計算結果基本相同，且大于實際值（有限元采用電流不均勻分布模型計算結果），這一方面驗證了IEC 標準的假設條件，另一方面也揭示了標準的局限性。隨著頻率的上升，趨膚效應和鄰近效應越發明顯，電流分布不均勻導致的損耗比率λ1也明顯變化，當頻率由分頻50/3Hz 增加到工頻50Hz 時，λ1誤差由14%增加到18.4%。

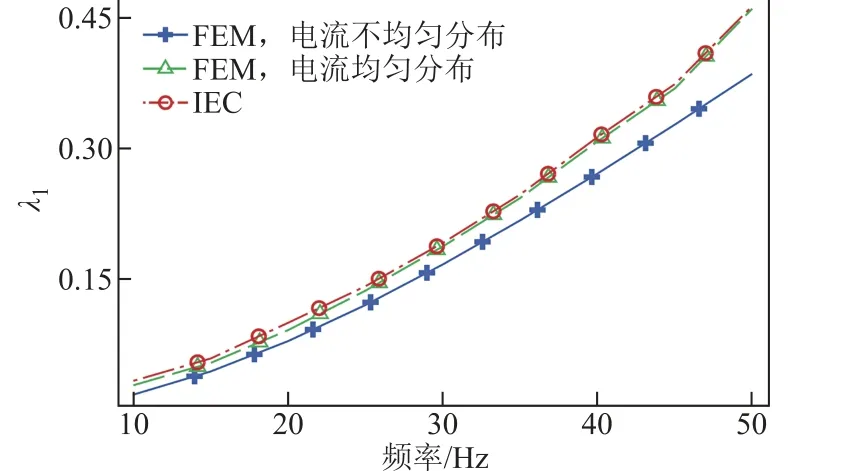
圖10 頻率對λ1 的影響Fig.10 Influence of frequency on λ1

除了頻率，纜芯半徑同樣影響損耗因子λ1，不同頻率時纜芯半徑對1λ的影響如圖11 和圖12 所示。在工頻輸電方式下，IEC 計算結果顯示，λ1隨纜芯半徑增加而逐漸增加，并存在飽和趨勢；而有限元結果則顯示，當纜芯半徑小于24mm 時，λ1隨纜芯增加呈增長趨勢，當纜芯半徑大于24mm 時，λ1則隨纜芯增加呈現下降趨勢，此時IEC 標準法誤差將進一步增大，究其原因在于，纜芯半徑越大，電流密度平均值位置和纜芯中心偏離越大，導致IEC 標準的電流集中分布假設和電纜實際電流分布情況相差較遠，從而導致IEC 計算結果誤差進一步增大。分頻輸電方式下，纜芯半徑對λ1的影響與工頻情況下類似。總之，電流的不均勻分布對損耗有十分明顯的影響，因此在計算電纜損耗時，應將電流分布情況考慮在內。

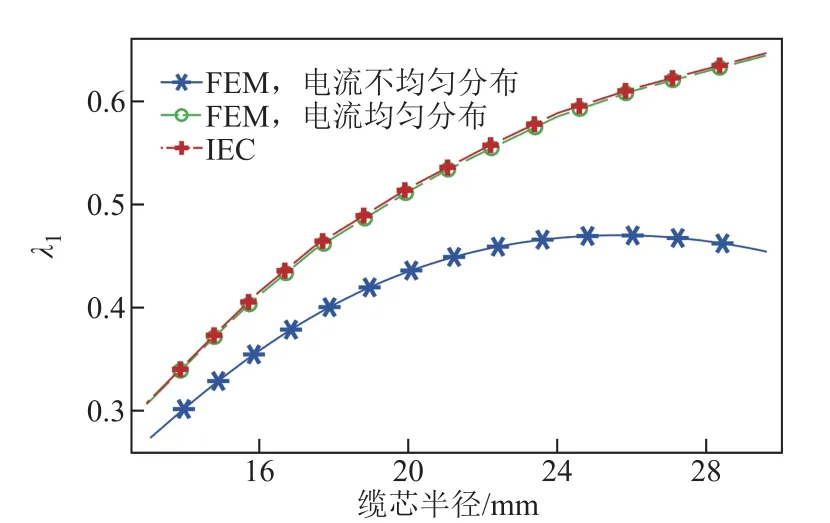
圖11 50Hz 時纜芯半徑對λ1 的影響Fig.11 Influence of core radius on λ1 at 50Hz

圖12 17Hz 時纜芯半徑對λ1 的影響Fig.12 Influence of core radius on λ1 at 17Hz

當同時計及護套損耗和鎧裝損耗時，采用有限元計算的電纜各部分損耗如圖13 所示，可以看出，隨著頻率的上升，電纜整體電磁損耗、纜芯損耗、鎧裝及護套損耗均呈上升趨勢。電纜總損耗比率如圖14 所示。

圖13 電纜各部分損耗Fig.13 Loss of each part of the cable

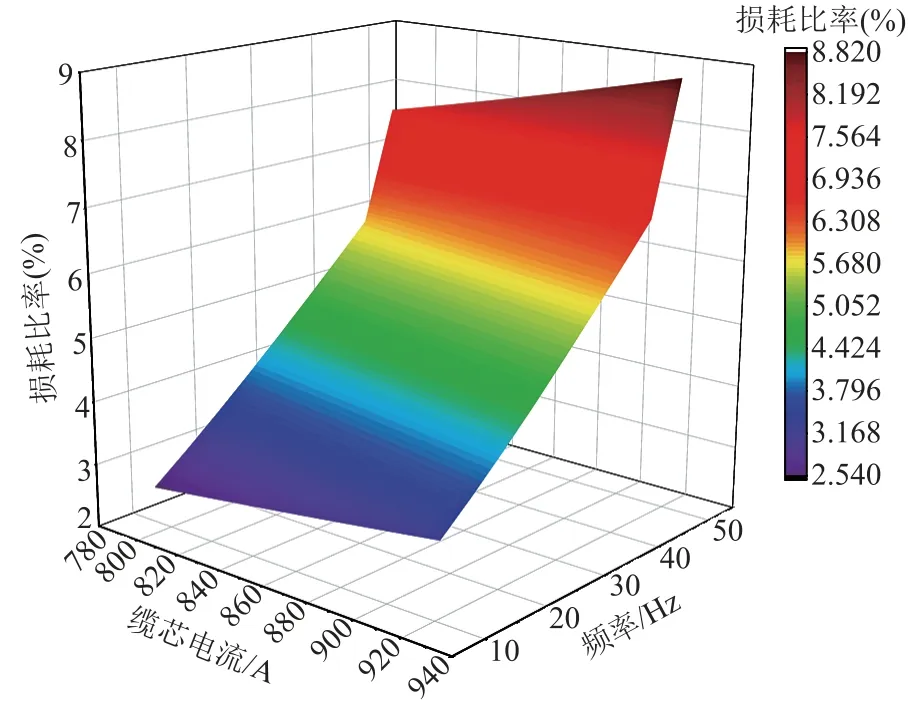
圖14 電纜損耗比率Fig.14 Cable loss ratio

2.4 載流量

基于上述分析，充分考慮纜芯電流不均勻分布，采用電磁-熱耦合模型計算得到的三芯鎧裝海底電纜的載流量如圖15 所示。

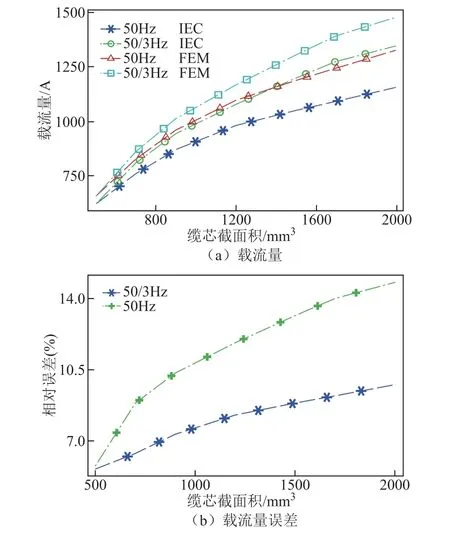
圖15 電纜載流量Fig.15 Ampacity of the cable

可以看出，相同纜芯截面積時，電纜工頻載流量低于分頻載流量；和有限元結果相比，IEC 計算結果偏大，隨著纜芯截面積增大，IEC 計算誤差有飽和趨勢，工頻時誤差最大值約為15%，分頻時誤差最大值約為10%。圖16 為三芯電纜滿載時的溫度場分布，此時纜芯溫度為90℃，溫度由內向外逐漸降低。

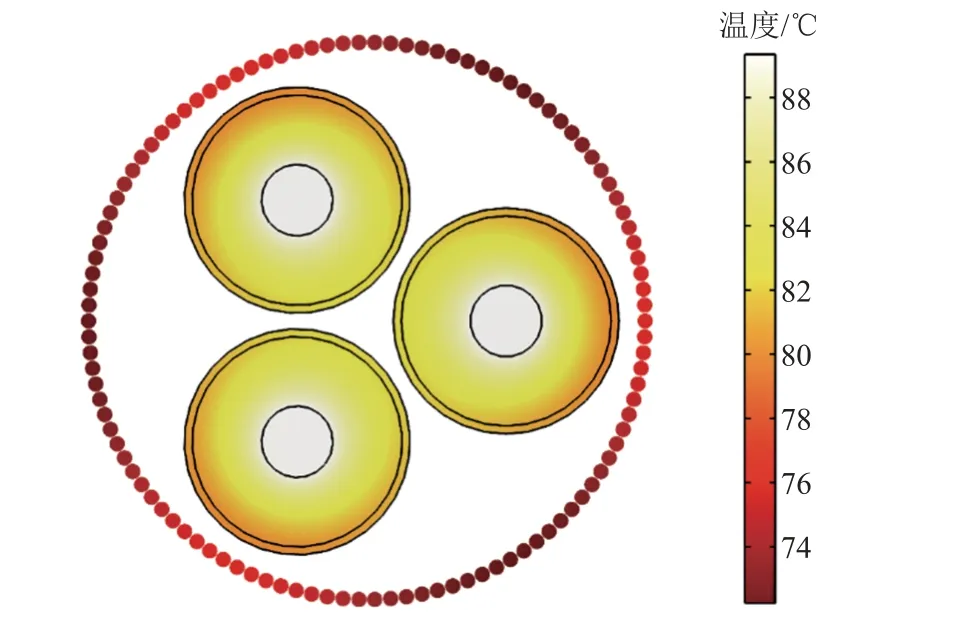
圖16 電纜溫度場分布Fig.16 Distribution of cable temperature

3 結論

本文基于電磁-熱耦合原理研究了三芯鎧裝海底電纜在低頻輸電方式下的損耗特性，得出如下結論：

1）纜芯電流密度平均值點偏離纜芯中心，偏離距離隨輸電頻率的增大而增大，此偏離距離是采用IEC 標準計算感應電壓、損耗因子和載流量時存在誤差的重要原因之一。

2）采用IEC 標準計算的三芯鎧裝電纜護套損耗因子λ1偏大，輸電頻率越高，纜芯半徑越大，λ1誤差越大，分頻及工頻輸電時誤差分別達到14%和18.4%；另外，當纜芯半徑增大時，實際損耗因子λ1變化規律呈現飽和甚至減小的趨勢，此時（半徑為24mm）由于IEC 標準計算誤差進一步增大，應慎重采用。

3）采用IEC 標準計算的電纜載流量偏小，該誤差隨輸電頻率和纜芯截面積的增加而增大，當截面積取2 000mm2時，分頻及工頻下的載流量誤差分別達10%和15%左右。