淺探抗差估計在水準數據處理中的應用

盧慶凱 王家峰

（陜西地建土地勘測規劃設計院有限責任公司，陜西西安 710075）

在水準網數據處理過程中常采用經典最小二乘法[1]，通過最小二乘法可以求得水準網的未知參數。使用最小二乘法的前提是水準網數據要服從正態分布，但是在實際工作和科學實驗中都有可能出現觀測粗差。對于出現粗差的觀測數據是不服從正態分布，因此去除觀測觀測數據中的粗差非常重要。抗差估計方法可以有效的去除觀測數據中的粗差，抗差估計理論是建立在觀測數據的實際分布，而不是理論分布上[2]。

處理水準數據時，當水準網的閉合差超限時表明觀測數據中含有粗差，僅僅從閉合差的角度尋找含有粗差的觀測數據是很難實現的，很難判定哪一測段的高差觀側值中含有粗差。

對于含有粗差的測量數據，往往需要進行大量的重測，重新計算觀測數據的精度以達到測量要求。數據處理方法中有些可以很好的探測到觀測中粗差，雖然這些方法能夠探側到粗差的存在，但是后續的數據處理中首先要剔除粗差然后才能大量進行數據平差，計算工作量較大。

抗差估計優于最小二乘估計在于抗差估計能探測觀測值中粗差的位置及其大小，并且能夠剔除粗差，獲得較高精度的平差結果[3]。在觀測值無粗差時，抗差估計與最小二乘估計結果相同。鑒于此，應當在水準網平差和平面控制網平差中應用抗差估計進行平差計算，這是比較容易做到的。

1 抗差估計原理

抗差估計又稱為穩健估計，它的作用是剔除實際生產過程中觀測數據存在的粗差，在數據處理過程中選擇合適的抗差估計方法可以有效的提高測量精度，使測量中的未知值最大限度接近實際值。我們的測量值是隨機變量，符合正態分布的，如果出現粗差（gross error）的話，我們在應用最小二差或卡爾曼濾波的時候就會使結果偏離真實值（濾波發散）的現象。解決粗差或系統誤差的時候，可以從兩方面去理解，均值漂移或者方差膨脹，抗差估計屬于方差膨脹模型，即均值不變，方差變化的現象。我們可以通過對出現粗差的觀測值進行降權處理。我們在實現的時候，這個權陣很重要，權陣也就是我們說的方差陣的逆，分為獨立和非獨立，即觀測值之間是否相關，是否相關也影響著等價權函數的形式。

2 抗差估計在實驗數據中的應用

如圖1，A、B、C 為已知水準點，HA=10m、HB=20m、HC=28m。正常觀測的高差及各路線的長度見表1，未知參數的解為: HⅠ、HⅡ在h1和h4上分別加粗差-10mm 和80mm 粗差，然后采用最小二乘法，計算相應的殘差值。

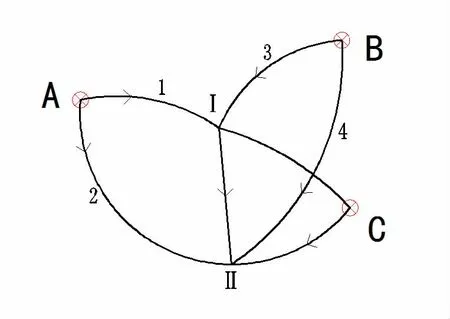
圖1 實驗水準網示意

表1 模擬觀測值

幾種方法的權函數雖然模型表達式一樣，但其目的都是為了檢測含有粗差的項[4]，并把粗差剔除。下面是幾種方法的權因子的收斂速度，如表2。

表2 幾種方法收斂速度的比較

分析說明：從上面可以看出幾種抗差估計方法中，IGGI 法權的變化符合我們的期望，能使含粗差的權變換逐漸趨于零；IGGI 法由三段組成，更適合測量計算。而丹麥權的收斂速度是最快的，且其最后收斂的結果可以滿足我們的要求，但其少淘汰段，不利于提高抗差能力。

3 三種方法實驗結果比較

表3 是幾種方法的平差值比較。

表3 三種平差方法的比較

分析說明：在幾種方法中，可以明顯看出抗差估計方法對含有粗差的平差值與最小二乘平差的方法的結果最近，且精度相對其他方法來說更高一些；粗差對改正數的大小在各個觀測值中影響可以看出對含粗差大的將會給其以大的粗差改正數，而對相對來說小的則會把粗差分配到了各個觀測值改正數中了。

從表4 中結果可以看出，各結果都有一定的抗差能力，IGG方案效果能滿足我們的要求，我們給測段4 加了80mm 的粗差，而IGGI 法在最終的結果中給其了81mm 的改正數，有效的起到了抗差的效果。

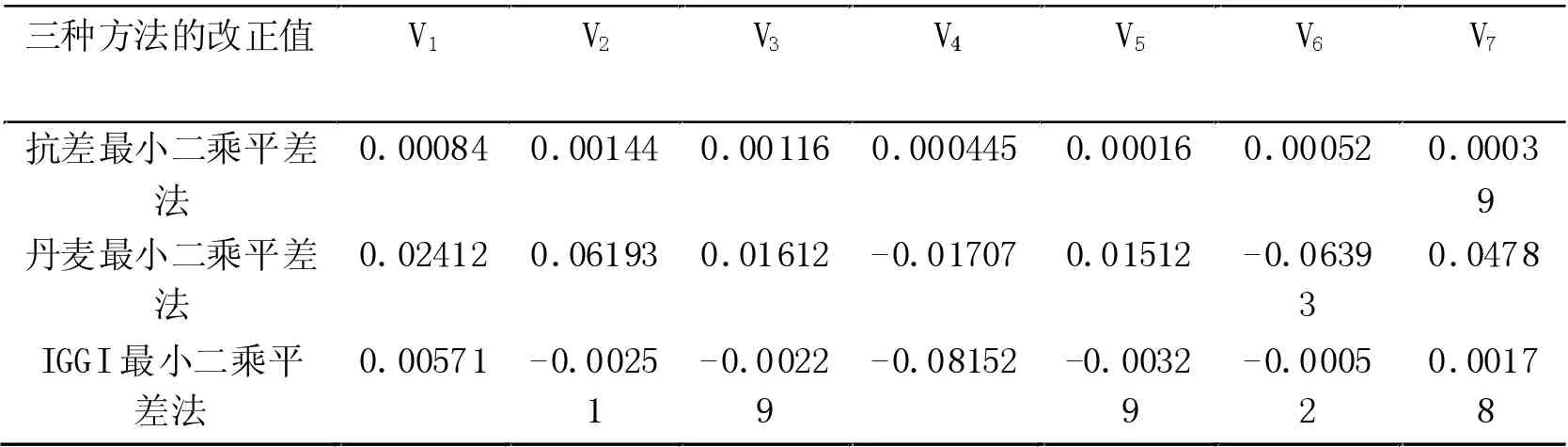
表4 三種方法的改正值比較

同樣為了提高實驗結果的可信性，對于實驗中設計的水準網。一是我們可以盡可能的增加水準閉合環路，增加觀測數量，得到更多的觀測數據，更多的觀測量有利于剔除數據中的粗差。二是提高觀測精度及實驗可靠性，當觀測數據含有粗差，我們發現并剔除時不影響繼續使用數據。

對于不含有粗差的觀測數據，使用抗差估計處理與最小二乘估計處理的結果是一致的[5]，從上可以看出最小二乘估計是抗差估計的一個特例。對于含有粗差的觀測數據使用抗差估計，一是可以準確的找出觀測數據中粗差的位置，二是可以剔除觀測數據中的粗差，提高測量精度。

4 結論

針對最小二乘法在系統量測數據存在粗差時出現的問題，本文把抗差最小二乘法應用于水準高程數據處理中，運用的多種經典權函數，對抗差結果得出常用的對于含有粗差的觀測數據使用最小二乘法效果不佳，當測量數據中存在粗差時，估計結果嚴重失真以至不能接受，甚至導致迭代不收斂。因此本文采用抗差思想，將抗差最小二乘法應用到水準測量高程估計中，通過實驗結果證明: IGGI 法更適合于水準高程數據中粗差的探測。