IT D 在探地雷達數據處理中的應用研究

孫權

（重慶三峽學院,重慶 404020）

1 概述

探地雷達是一種利用超寬帶電磁，探測技術，用于對位于地面下，或不可視物體中的物體進行定位和分析的技術[1]。在探地雷達數據處理中，噪聲的有效去除是后續處理中目標識別和成像的基本保障。

在傳統探地雷達信號處理，多將信號視為平穩線性的，采用基于Fourier 分析的方法進行去噪處理。然而，在使用探地雷達進行實際探測的過程中，探測方式、探測環境和探測系統的干擾和波動，導致了接收到的信號具有非平穩、非線性的特征[2]。對于非平穩非線性信號，Fourier 分析方法具有不可避免的局限性。Fourier 分析采用線性疊加正弦波，來模擬波形形變，對于非線性非平穩信號，數據往往會偏離純粹的正弦或預先函數，在傅里葉譜中產生額外的諧波分量；同時，傅傅里葉分析將分量的范圍定義在整個時間尺度上，從而使得能量分布在整個頻帶范圍上，從而產生虛假諧波和寬頻譜，導致分析結果不能忠實的表達實際的時頻分布關系。這些因素限制了Fourier 變換在探地雷達信號分析中的應用[2]。

Huang 等人提出了經驗模態分解（empirical mode decomposition，EMD），用于處理非線性非平穩信號[3]。研究者們開始嘗試將EMD 方法應用到探地雷達信號處理中，取得了良好的效果；王超，沈斐敏使用EMD 方法有效的去除了探地雷達中的直達波，根據PGR 直達波的特點，引入差異擴大和能量均衡的理念，采用EMD 方法有效的取出來直達波干擾[4]；王韻棋等人將EMD 用于處理車載探地雷達信號處理，對路基檢測中的高頻噪聲進行壓制，取得了良好效果[5]；馮德山，戴前偉采結合黑麋峰抽水蓄能電站進場交通軌道實測GPR 刨面，詳細分析了信號的瞬時譜特性，通過瞬時參數的刨面圖對地質情況進行解釋，突出刨面中的異常特征，以提高對GPR 信號的分析效果與解釋精度[6]；楊建軍等人，將EMD 與小波閾值法進行對比，通過分析認為EMD 無論是信噪比還是均方誤差都優于小波閾值法。[7]

雖然EMD 方法能夠自適應處理非平穩信號，并在GPR 信號處理中取得了良好的效果。但是在EMD 分解過程中，每次篩選都會導致窗口邊界或邊緣效應向內傳播，阻礙其提取時-頻-能信息的能力。而且EMD 使用插值來獲得上下包絡，進而獲取基線，也使得EMD 繼承了在插值過程中產生的偽極值，導致失去部分信息，在結果中出現虛假的相移和失真。2007 年，Mark G. Frei 和 Ivan Osorio 提出了固有時間尺度分解（Intrinsic Time-Scale Decomposition，ITD） 的概念[9]。它克服了EMD 和傅里葉分析等經典方法的局限性。ITD 繼承了EMD 算法的優點，弱化了模態混疊等現象，減少了復雜的篩選和樣條插值，提高了信號處理效率，可以實時反映頻率變化[10]。

本文將ITD 方法用到探地雷達信號處理中，將GPR 信號進行ITD 分解，通過對PRC 分量的選取和重構，去除信號中的噪聲，通過正演模擬實驗和實測實驗，表明ITD 方法能夠有效的去除噪聲，且相較于EMD 方法具有更高的準確度。

2 固有時間尺度分解

ITD 算法是一種高效、精確的時頻能量分析算法，ITD 將非平穩復雜信號分解為一系列具有實際物理意義的固有旋轉分量（Proper Rotation Component，PRC），可以直接根據結果得到瞬時頻率和相位。其分解過程描述如下：

通過ITD 處理，信號被分解為一系列PRC 分量，信號和噪聲根據其自身瞬時頻率譜特性，分布在這些分量中，通過將信號所在的分量進行疊加重構，從而去除信號中所包含的噪聲。流程圖如圖1 所示。

圖1 ITD 處理GPR 信號流程示意圖

3 實驗及仿真分析

3.1 克雷子波分析

在探地雷達信號中，克雷子波是其中的基本的組成信號，對其進行處理的結果具有一定的代表性。因此，通過在Matlab中對添加白噪聲的克雷子波進行ITD 處理來驗證ITD 方法的有效性。首先將克雷子波添加噪聲，并進行ITD 處理，然后選取其中由信號主導的分量進行重構，從而實現信號去噪。分量的選取會影響去噪結果，在EMD 方法中，有經驗觀察法，自相關函數法，灰度相關等方法對分量進行選取[11]。采用不同的方法選取分量，重構結果并不相同，因此需要結合實際情況進行選擇。本文選用經驗觀察法對分量進行選取。仿真結果如下所示，其中圖2 為無噪聲的克雷子波，對其添加信噪比為-10.01DB 的噪聲，見圖3。經ITD 方法進行分解重構，信噪比提升為-0.52DB，見圖4。

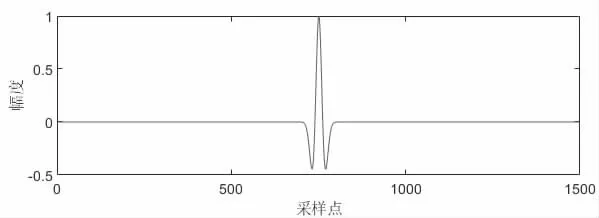
圖2 原始信號

圖3 加噪聲后的信號

圖4 Ricker 信號去噪結果

圖5 為ITD 和EMD 去噪結果中信號峰值位置的對比。經過ITD 方法去噪處理后，信號峰值點的位置與原始信號峰值位置保持一致，而EMD 去噪信號的峰值位置存在一定的偏移。可以看出ITD 方法相較于EMD 方法，能夠有效的保證去噪后信號在時域上的精度。

圖5 去噪結果與源信號峰值位置對比

3.2 正演數據分析

為了驗證ITD 算法對B 掃數據的去噪效果，通過電磁仿真軟件GPRmax 生成正演數據，并添加噪聲，對所提方法進行驗證。圖6 正演仿真為源信號，添加噪聲后信噪比為-4.99DB，見圖6 正演仿真，并采用ITD 方法進行去噪處理，結果見圖6 正演仿真，信噪比為0.45DB。通過正演數據分析，結果表明ITD 方法可以有效去除探地雷達信號中的白噪聲。

圖6 正演仿真實驗結果

3.3 實驗測試

在實驗室內，搭建沙箱進行測試，獲得實測數據。探測設備采用中國電波所LTD 智能化探地雷達進行測試。測試沙箱長1.8 米，寬0.5 米，高0.6 米，沙子厚度約0.5 米，其結構如圖7 圖所示，在沙箱中預埋直徑為5cm 的403 不銹鋼金屬球進行探測，獲得圖8 所示結果。在測得數據中加入強干擾，進行去噪。結果見圖9。加噪后信號的信噪比為-4.99DB，去噪信號的信噪比為-2.40DB，可以看出經過ITD 去噪后，信噪比有所提升。

圖7 實驗沙箱

圖9 實測數據實驗結果

4 結論

本文對ITD 方法在探地雷達信號去噪中的應用進行了研究，對探地雷達A-scan 數據進行ITD 處理，采用經驗觀察法選取分量重構，通過正演模擬數據和實驗數據進行驗證，ITD 方法可以去除探地雷達信號中的噪聲，相較于EMD 方法在時域上具有更好的精度，避免了峰值漂移。與其他的模態分解方法相同，想要進一步提升ITD 的效果，除了方法自身的改進，同樣需要面臨分量選擇和分量處理的問題。精準的分量選擇方法和合適的分量處理手段能夠進一步提升該方法的實用性能，也是后續研究的方向。