中國三十年來小學階段分數研究文獻的系統分析及啟示

黃曉林，黃秦安

中國三十年來小學階段分數研究文獻的系統分析及啟示

黃曉林，黃秦安

（陜西師范大學 數學與統計學院，陜西 西安 710119）

文獻系統分析發現，圍繞教與學形成側重作為知識的分數和關注分數認知事實兩條不同研究主線，且偶有交叉，反映了傳統教育“教學圍繞教師發生”特點的影響．以分數教學研究為透鏡，探討以學生分數認知為基礎進行教材編排，由測量模型引入分數概念的可行性，體現教育研究對學生學習的真切關懷．提出基于“學”展開數學知識探討以豐富知識內涵；關注學生學習發生真實過程以改進教學實踐；深化數學學習評價以促進學生核心素養培養；強化教師數學教學觀以指導教學實踐研究，為數學教育提供借鑒．

分數概念；分數教與學；教材編寫；測量模型

對“數”的認識與學習是小學數學階段的重要內容，學生的學習“不僅包括數學結果，也包括數學結果形成的過程和蘊涵的數學思想方法”[1]．相對于自然數而言，分數的學習明顯地表現出“承上啟下”的性質[2]．分數異于自然數的符號特征與其自身豐富內涵增加了學生學習的難度．無論從數系擴張的角度，把握分數作為數的本質屬性，兼顧其產生的歷史進程及教學啟示；還是從學生數學思維發展的角度，理解學生分數認知規律，為學習與發展構建基礎，都對分數學習產生重要影響．因此，不難理解分數作為小學數學教學中一個具體內容，卻引起了心理學和教育學學術研究者、教研員和一線教師的廣泛關注．近30年來，研究者透過不同的視角，采用不同的策略與方法，在教學實踐與學術研究中成果豐碩．作為數學教育領域眾多重要議題中的一個，其研究結果中既有作為分數教學內容特有的典型特征，也有中國基礎教育階段共有的特點，以此審視小學數學的“教”與“學”，進行分數研究知識脈絡的系統分析，為后續數學教育研究積累些許經驗是有意義的．

選取CNKI收錄的732篇（其中57篇核心期刊來源文獻）小學階段分數研究文獻，采用系統分析的方法，梳理了分數主題研究的知識發展脈絡，勾勒知識演進過程；聚焦分數研究的核心問題，審視分數教學研究是否符合學生的認知發展和教育目標；探討學生“學”與教師“教”之間怎樣實現更好的互動，以推動學生自主學習，實現全面發展．

1 中國近30年分數研究主題文獻要素的整體分析

從作者身份上看，將研究者分為，一線教師為主的教學實踐者、教研員為主的教師教育者、高校教師為主的學術研究者3類．從研究涉及的內容上看，具有典型特征的教學實踐者關注到了分數教學的幾乎全部內容，編碼頻次由高到底分別是分數的運算、分數的應用、分數的認識、分數的意義、分數基本性質以及分數的表示．在這些工作中，教師嘗試以具體知識內容為載體探討分數教學問題．而學術研究者的工作中，少部分同教學實踐者一樣，聚焦分數具體知識，如分數運算中的除法、分數大小的比較、解分數應用題；多數工作關注分數概念的本質含義，在教材中的編排與呈現，兒童分數認知發展．

從研究視角上看，教學實踐者多借助具體的教學設計和課堂實錄進行教學片段分析、課堂教學活動反思，闡釋教學案例背后的教學方法和理念，且具有較高同質性．相反，學術研究者較少關注具體內容的教學實踐問題，而是通過分數概念內涵的探討、教材比較等方式獲得對分數本質的認識；關注學生學習中分數概念的理解、發展與建構，以及對學習結果的評價；基于心理學科視角，對兒童學習分數概念的認知思維、表征方式、學習加工模式等進行實證研究．

2 分數研究的知識演進脈絡分析

從分數研究的文獻增長量上考察分數相關研究的整體進展，發現1991—2000的10年間僅6篇文獻在核心期刊上發表，主要研究工作集中在2006—2020年．以《小學數學參考》連續26年的發文量與所檢索到的核心期刊文獻數量變化比較發現，進入21世紀后關于分數的研究似乎淡出了研究者的視野．其中，2000—2005年檢索CSSCI期刊文獻數量為0．盡管2006年前15年發表在核心期刊上的文獻不多，但研究工作呈現出聚焦學生分數學習的特征：一類關注教學實踐中學生的分數計算和問題解決，關心學生成績；一類基于心理學視角，關注兒童對于分數的認知加工和表征，考察學生對于分數的理解．以下重點探討近15年來的知識演進脈絡．

2.1 分數研究的近15年知識演進過程

縱觀2006年后的研究工作，“數概念”成為關鍵詞聚類的中心，表明認識分數概念的本質逐漸成為研究工作的立足點，分數中諸如“分數概念”“分數乘除法”等具體問題是多數研究繞不過的載體．研究主題圍繞著“教”與“學”形成了兩條研究主線．

2.1.1 圍繞教學展開的研究

在“怎樣教”的問題上經歷了關注教學設計和具體教學問題；探討整體教學結構；聚焦承載“教什么”和指導“怎么教”的教材比較研究3個階段．探討“怎樣教”的過程中，研究者或從兒童分數概念學習的發展階段及困難點出發[3]，或基于當前分數教學模式，由學生分數除法、分數意義的理解層次[4–5]，建構文章分析和測量框架，從學習結果出發展開研究，反觀學習不足，提出具體改進建議．如，強調重視學生對分數及各部分概念和意義的深刻理解[6–7]．或圍繞分數教學中應“教什么”進行概念辨析，厘清分數概念的本質與內涵[8–10]，提出“模式主導，雙向多維”的分數意義的整體教學設計方案[11]和具體的教學實踐改進策略．如，從度量模型引入分數單位[12]，展開行動研究[13]，推進研究者對于分數概念與教學的深入理解[14–15]．

在聚焦“教什么”和“怎么教”的教材比較研究中，研究者就具體的分數內容對中、美及新加坡教材中定義類型、表征方式和編排順序做了比較研究[16]；在整體內容的編寫依據、組織結構，以及教科書編寫理念和呈現方式等方面的比較亦有涉及[17–18]；中、日、新加坡，中、韓，以及中國大陸和中國臺灣地區教材中例題和習題及分數除法內容編排的比較，橫向上進行內容組織對比分析，縱向上對不同版本教材的難易程度，知識點呈現的認知深度，學生認知發展進行了研究[19–22]．此外，研究者還透過不同的理論視角反觀現有教材，提出編寫建議[23–24]．

2.1.2 圍繞學習展開的研究

關于學生分數學習困難和學習認知的研究，最初延續關注學生分數學習結果，圍繞學生分數學習困難的思路[25]，反思學生在分數學習中對等分、單位量、等值分數等概念理解的發展階段與實際困難，認為“整數偏向”是兒童學習分數的抑制因素，并探討教學實施策略[26]．隨著研究的深入，對學生分數學習困難的研究視角逐漸由借助學生的分數學習結果反觀學習困難，轉變成考察學生分數學習具體問題，嘗試從心理學角度解釋學習困境．如，學生通過“部分—整體”模型習得分數概念后形成的誤區及學習困難[27]．

在分數認知方面，通過實證研究對兒童的分數概念認識、分數表征，以及認知加工方式等進行深入探討．從關注個體學習出發，梳理了兒童建構分數概念時所采用的分割計數和相對量的知覺兩種心理基礎及建構機制，對分數概念語義理解水平和模式進行深入探討[28–30]；嘗試從兒童思維發展水平和對等值分數語言認知兩個方面，解釋兒童在理解等值分數概念時的困難，將小學一～三年級兒童等值分數概念的發展劃分為整體量概念、數量化的相對量概念、正式的等值分數概念3個階段；設計并實施干預實驗，提出嘗試開展等值分數的早期教學，從小學低年級入手，在個體的非正式整體量基礎上逐步推進對正式概念的學習；通過讓兒童關注等值分數任務情境中各對應維度之間的乘法關系，能有效促進兒童乘法思維發展的具體教學建議[31–32]．在分數表征與認知加工方式研究方面，聚焦兒童非符號材料上的分數表征方式[33–34]、分數數量表征的準確性及形式[35–36]、分數估計的表征模式[37]、分數表征轉化能力[38]、整數數量表征與分數數量表征的關系[39]、在分數比較或解決分數應用題的認知加工方式等[40]，通過被試的表達，對問題測量結果進行統計分析，得出兒童分數表征和分數認知的事實結果．其中，分數教學的宏觀指導建議詳見結果討論部分．

2.2 分數研究的知識主線分離

值得注意的是，將學術研究者的研究工作分為“分數教學及分數學習”和“學生分數認知”兩組，分析文獻共被引發現，研究者僅在討論小學數學中分數的多層級理解[10]及整體構建分數意義的教學行動研究[13]，引用了學生分數概念認知的相關工作．另一邊，僅一項五年級和六年級學生分數表征轉化能力的調查研究[38]參考了已有分數教學問題的相關結果．這反映出，一方面，心理學研究工作關注學生分數認知的事實規律，卻較少關注認知規律對教學活動的真實影響，這可能與心理學科研究者的科研工作多從學術角度出發，對實踐關切不足有關．另一方面，教學研究關注的焦點在于知識層面的概念與內涵，忽視學生認知能力狀態，多從“教師教”的角度，基于實踐思維考察分數教學的相關主題，忽略學生自分數學習之始已將其先前經驗（如幼兒早期對于非符號分數的計算能力、整數計算能力等）帶入學習中的事實，對學生作為學習的積極參與者和知識的共同建構者在學習活動中的主體性關注不夠．

從數學教育傳統來看，可能是在教與學的統一活動中，普遍重視教多于重視學；基于“跟我學”思維邏輯展開學習指導與實踐研究，是“我教你，你去學”，而不是“你去學，我適時、恰當地教”；漠視學生學習真正發生的過程，疏于反思教的本質是為了促進和幫助學生更好去學的事實．從中國教育的歷史中考察，教學大致圍繞著教師來發生是傳統中國教育的一個十分重要的特色[41]．傳統教學中，通過會話或對話的方式來教學，一方面使因材施教得以實現，另一方面強化了教學方式中教師引導的重要地位．隨著社會工業化的發展，傳統的小組式學習和師生會話的教學方式面臨著整班教學的挑戰；規范的學科知識體系，細致明確的教學目標，定時定量完成的教學任務，沖擊著教師因材施教的可能性．然而，教學圍繞著“教”展開的認知卻在撕裂了的師生雙主體的傳統教學形式中保存了下來，使得教師教與學生學的統一活動中，呈現出對“教師教”的思考多于對“學生學”的關注；教學內容依據教學計劃展開，忽略學生學習的真實需求；教學方法依據教學內容選定，漠視學生學習真實發生過程．伴隨著信息化時代的浪潮，關注每一個學生的學習再一次成為教學的方向和可能．因此，嘗試從教學活動的另一面，“學生學”的視角探討分數研究主題是未來研究的新動向．

3 分數研究的重要問題梳理與討論

如前所述，通過對文獻的系統分析，從教師、學生和分數教學內容，及3者相互聯系的角度，立足于溝通教師與學生、學生學習與所學內容，嘗試勾勒分數研究的知識脈絡．對于研究者重點關注的分數概念的內涵，學生的分數認知、教材編排、分數教學等議題，以分數教材的編排與分數概念的引入為抓手，做進一步梳理和闡釋，探討基于“學生學”的教材編寫和分數概念引入．

3.1 分數教材編排：分數的概念意義或學生的分數認知

3.1.1 分數的概念意義

在學生的分數學習研究中，研究者傾向從分數的意義出發探討分數是什么而決定學生需要學什么．對于分數意義的研究多參考Kieren對于分數概念解讀的5個方面：整體與部分的關系、比、商、測量與運算符（operators）[42]，發展出對分數的不同解釋．張奠宙先生用“份數”解釋分數定義與除法的包含除、平均分的關系，強調“先將整體平均分成若干份”是等分除角度的定義，“部分占整體大小”是包含除模型[43]．Kieren也認為，比的關系包含了“整體與部分關系”與“部分與部分關系”兩種解釋，提出分數“整體與部分關系”的解釋是“比”的一種特殊情形，同時強調了兩種思維方式在認知心理上的不同．也有研究者放棄整體與部分關系的含義，探討分數作為比、商、測量和運算的4種解釋方式[3，13]．從數系擴張的角度看，用兩個線段長度比表達分數，是用幾何的方法解釋無理數[44]；分數純數學上的定義，是指兩個整數相除的商[3]，即表示兩個數關系的數．

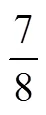
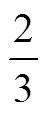
3.1.2 學生的分數認知

分數認知是數學認知研究的一個關鍵領域，從兒童認知角度來探討其理解分數困難的形式和原因是近年來國內外分數研究關注的重要主題．其中，整數偏向（whole number bias）[46]是指學生趨于穩定使用有關整數的獨立單元計數圖式來解釋分數的傾向，被認為在學生的分數認知中普遍存在，主要體現在比較分數大小、排序和分數的加減法運算上[27]，它是否是兒童分數學習困難的影響因素？ 中國研究者在這個問題上的研究，首先關注到教學實踐中整數偏向對于學生分數學習的負面影響[47]，梳理了整數偏向的可能成因，即學生在構建分數概念時新舊知識之間的干擾和數字認知的起源和發展的更普遍問題．其中與分數教學相關的因素是，教師在教授分數概念時從部分—整體引入，強調了整數概念，造成學生對分數測量含義的不理解，教授分數比較和運算時，用先前的整數策略使學生更快捷地習得解題方法，雖為學生從整數系統擴展到有理數系統提供了很好的橋梁作用，但也為整數偏向的出現提供了可能性[27]．研究者測查55～75個月幼兒非符號的分數和整數計算能力發現，避開符號的干擾后，幼兒的分數計算能力盡管略低于整數計算能力，但遠好于隨機水平，且兩者具有相似的發展模式[33]，排除了整數偏向發生的認知起源和發展因素，將發生的可能因素聚焦在分數學習過程的影響上．進一步，通過對小學生在非符號材料上的分數表征方式的實證研究發現，放棄分數符號轉用非符號性分數材料，排除了整數的影響時，被試可以很好地完成分數比較任務[34]．這促使研究者反思，整數偏向或其它系統性的誤解并不是影響學生學習分數的主要因素，不準確的類比才真正阻礙了學生的學習．并提出了在教學中密切聯系幼兒的早期分數經驗[33]，考慮將分數教學提前，甚至可以和整數知識同時教授給學生的教學建議[28，34]．

盡管國內研究者從兒童認知層面關注到整數偏向問題的時間較國外晚，但隨著研究的不斷深入，后續的工作進展與國際研究工作幾乎同步．研究者基于Siegler等提出“分數和整數的理解之間具有關鍵的連續性”[48]的觀點，進一步發現，兒童與成人在不同的數字線上的分數表征與整數表征結果非常類似，并認為分數作為一種數量符號是對整數符號的擴展[37]；分數與整數的數字線任務的研究證實了五、六年級學生整數數字線估計對分數數字線估計的積極預測作用，說明整數數量的理解是分數理解的重要前提[39]．上述研究不僅解釋了整數的認知不會抑制分數的學習，相反，強調了分數的測量意義對于兒童理解分數和整數的聯系和相似點的益處，為合理地安排學習內容，促進學生將整數的認知擴展到分數等其它類型數概念的理解提供了理論基礎．

3.1.3 教材內容編排的研究述評

中國教學實踐活動對教材依賴程度較高，教材的編排方式往往對教和學產生較大影響．研究者通過對不同國家及版本教材的對比分析，對分數教學內容編排提出指導性建議；通過關注分數內涵及其歷史演變過程，聚焦分數知識本身在教學中的重要作用，從教育工作者期望達成的教學目標出發，圍繞分數認知模型、任務設計、材料提供、習題選擇、課時保證對教材內容進行編排．然而此類研究落腳點在教師的教學，而不是學生的學習，是知識本位視角的探討．盡管有研究者關注到教學內容的編排應關照不同年齡段學生的認知特點，從認知復雜程度及認知深度出發對分數教學內容進行適切性調整，但是這樣的研究從學生認知發展的一般規律出發，并沒有真切地反應出學生在具體分數學習過程中產生學習困難的原因及心理因素．

促進學生學習發生是教材編寫的核心任務，關注分數概念意義與學生分數認知是在“分數”內容和學生學習之間搭建橋梁的基礎．教材編寫從分數的意義出發，不能僅落腳于分數知識，需從學生分數學習出發關注兒童分數認知的真實狀況．關于分數認知的研究中，學生的分數概念語義理解水平，對分數的認知和整數認知相互聯系的關系；“部分—整體”認知模型帶來的整數偏差；測量意義上分數概念理解的重要性；分數作為“數”的概念對于理解分數和分數運算的重要作用等，對于指導兒童的分數學習具有重要的意義．教材編寫不能僅依賴“分數概念本質”這一知識本位的編寫思路，更應關注學生分數學習的真實困境，考量分數認知發展的研究成果，區別作為學生學習的分數知識與分數知識本身之間的差異，體現教育研究對學生學習的真實關懷．

3.2 分數概念的引入：“切蛋糕/分桃子”模型或測量模型

3.2.1 分數概念引入教學的現狀

考察已有98份“分數認識”相關文獻，從涉及的人教版、北師版、蘇教版教材的分數概念定義來看，人教版教材強調“將整體平均分為若干份”，分數是指“取其中一份或幾份”，北師版和蘇教版教材從單位“1”的角度對整體所表達的含義不僅包含“一個物體”，還包含“把多個物體看作一個整體”做了說明，從部分—整體的視角引入分數概念，更多關注到的是分數“作為整體的部分”的含義，淡化“整體”與“部分”的關系．基于文獻中的教學實錄、教學設計，教學片段反思可知，分數概念教學多采用區域模型（分割一個具體的圓等圖形或實物）和離散物體模型（分一堆桃子等實物）為表征方式呈現學習活動，從“不能夠用整數恰當表達一個數”的教學情境出發，引發學生認知沖突，借助“部分—整體”模型引入概念．教學反思時，教師關注具體情境中學生的學習過程對于促進數學思考的影響；探討直觀演示、操作活動對于提升學生數學活動經驗及形成分數概念的教學效果．鮮有教師關注到學生的分數認知基礎和認知結構，通過學生解決分數問題的方法對其思維過程進行合情推理．

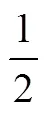
3.2.2 分數概念構建機制

對于兒童來說，進入分數學習之前可能是帶著關于分數的相對量大小的知覺，或分割（split）和迭代（iterate）的先前經驗的．兒童在其發展早期，可能基于類比數量表征能力來籠統認識分數量的大小，而在發展后期，可以基于分割計數操作來實現對分數量大小更為精確的認識[28]．從學生學習的角度考察其分數概念如何在個體先前經驗基礎上建構而成，能夠從分數認知層面為更合理的引入分數概念，為優化分數教學提供心理學的理論基礎．研究者在梳理了Tzur的反省抽象過程和Kieren的遞歸過程這兩個分數概念的個體建構理論發現，Tzur借用了皮亞杰提出的反省抽象，并具體說明了個體如何從自身的分割動作之中抽象出分數概念的部分—總體含義，是分數概念建構的過程模型；而Kieren將分數概念的建構機制比喻為邏輯上的遞歸過程，側重于強調分數概念建構的不同層次及層次間的同構關系，即高層次理解是對低層次理解的拓展，是分數概念建構的層次模型[28]．

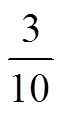
在分數概念層次理論上，研究者綜合分析了Kieren的分數概念層次結構理論、Behr的分數概念語義結構論和Vergnaud的分數概念域理論，嘗試依據3種理論試圖解決的分數概念的多個含義關系和分數概念不同含義與分數運算任務之間關系為理論框架，探查兒童對于分數概念語義理解的水平[30，50]．一個有趣的結果是，中國學生語義含義的理解水平上，學生理解和掌握水平最高的是商的含義而不是部分—整體含義，與理論之間存在一定的差異，也從側面反映教學干預對于學生認知發展的影響．

3.2.3 從測量角度引入分數概念的可行性探索

事實上，從分數知識的抽象程度來看，分割和形成分數單位是進行復合單位運算的基礎，對分數單位的正確理解是進行分數概念學習、運算學習的關鍵和核心．而如何看待“分數單位”這一重要概念是“切蛋糕/分桃子”模型區別于測量模型的關鍵之處．換言之，“分數單位”是一個來自整體的部分的分數，還是獨立于整體之外，和整體之間存在倍數關系的分數，是兩種分數概念建構方式的沖突所在．基于學生分數認知發展特點，從學生數概念擴展的角度來看，建立分數單位概念基礎將更有利于學生思維結構的發展，而將測量單位看作是分數概念的起點，能夠較為合理地解釋分數的起源以及用乘法推理思維解釋分數的運算．

4 分數研究主題進一步探討及啟示

分數作為小學數學教學的重要內容，其典型性和代表性不言而喻，以上通過與學生分數學習緊密聯系的教與學研究的立體考察，可清晰地看到研究者對“教師教”與“學生學”非二元對立的理解，以及分數作為學生學習的具體知識內容，為教師教與學生學的活動建立起自動聯結的關注．以下進一步探討與分析分數研究主題，為中國數學教與學的研究提供一個反思性的視角，也為數學教育研究工作提供些許經驗和啟示．

4.1 基于“學”的知識探討是應然視角下內涵分析的有益補充

對于教學而言，“教什么”和“學什么”是構成教與學活動的核心基礎之一，對分數本質認識的深入探討是必要且重要的．然而，已有研究多是分數知識角度展開的應然探討，較少見到對學生分數學習實然角度的關注．研究者不僅需要關注分數概念的部分—整體關系，比、商、測量、運算符等模型意義；從分數概念本質的角度厘清學生學習的分數知識具有怎樣的結構和含義；處于小學階段“數與代數”知識框架的何處，對于后續有理數學習有著怎樣的基礎意義；也需要探討學生在自身分數概念建構中分數數感的建立、分數大小的理解；以及分數計算，特別是除法學習過程中，由于分數與整數、分數除法和整數除法相類似的概念結構，受到整數先驗知識干擾導致的整數偏向對分數學習的影響．因而，從“學”的角度對于知識的探討是應然視角下對知識內涵分析的有益補充．

4.2 關注學生學習的真實發生是改進教學實踐活動的基礎

關于分數內容“怎么教”，一直是學術研究者和教學實踐者共同關注的議題．學術研究通過教學設計的整體架構和教材內容的編排研究對改進分數教學提供指導建議；教學實踐則更多關注教學環節操作層面的改進．事實上，研究者在教學研究活動之前，已經對分數概念有了深刻理解，甚至形成了對分數理解的固有模型，作為知識的已知者，在進行教學設計時常著眼于如何將知識概念以符合教學一般規律的方式，邏輯清晰、條理分明地呈現出來．換言之，教給學生的是教師認為恰當、合適的數學，往往忽略了學生作為學習主體，其自身所具備的學習經驗和概念基礎，使得教師的教與學生的學淪為兩個看似融合，實則獨立的活動，教學實踐改進難有本質突破．關注學生學習真實過程中的認知困難和學習困境，有針對性地開展教學實踐或許是跨越“教”與“學”鴻溝的有效方式．因此，理解學生的數學認知不能僅僅是學術研究的議題，以學生數學認知研究結果與方法為基礎，與教學實踐中的具體困境相結合是改進教學實踐的方向之一．

4.3 基于學生學習的評價是促進學生核心素養培養的風向標

在分數學習評價方面，研究者從學生分數學習結果出發，反思學生分數學習中學習困難，反觀學生的分數認知狀態，卻較少有對學生分數學習過程監測、思維發展等議題的探討．譬如，研究者關注到學生分數計算的準確性和流暢性，卻忽略學生的計算能力來源于對計算程序性知識的熟練掌握，還是對分數運算概念的理解，抑或是兩者相互支持的結果．研究者關注到學生在解決分數問題，特別是分數應用題中對分數單位概念的迷思，缺乏問題解決意識等現象，卻鮮有關注分數問題解決背后學生數學思維的發展，忽略學生分數概念建構的認知理論和認知基礎．換言之，在強調應讓學生學會理解分數概念，學會分析問題和解決問題的同時，忽視了分數概念培養與學生數學思維發展相聯系的契合點，如，單位分數概念的建立與乘法推理思維發展、分數計算與有理數計算的合理類比等．評價導向是當前教學實踐活動的現實起點，基于學生學習過程的評價研究，實現學生學習評價過程和結果的統一是未來研究的重要議題．

4.4 教師的數學教學觀研究是指導教學實踐活動的前提和保障

在分數教學的研究中，一方面，職前和職后教師是否具備理解分數概念，解釋錯誤分數模式的知識，理解學生在分數學習過程中特殊的認知過程，選取恰當的教學方式是研究者關注的重要議題．另一方面，教師應具備怎樣的分數知識、分數教學知識，以及學生的分數學習知識以支持其在教學活動中做到尊重、理解學生關于分數的先前經驗并指導學生的學習活動，也是關于分數研究的一個重要的、國內相關文獻研究較少涉及的主題．此外，關于教師分數教學知識的研究中，研究者也注意到教師所具備的理論知識和實踐經驗的差距，其中典型的表現是，教師具備的分數教學知識與單調傳統的教學實踐行為的不一致．在教師具備豐富的學科教學知識對學生學習具有積極影響是教師教育領域的重要共識下，關注職后學習如何促進教師的學科教學知識和教學信念的發展，教師所具備的學科教學知識如何對數學課堂教學實踐產生影響，是教師形成數學教學觀的前提，也是教學實踐活動順利展開以促進學生的數學學習與素養提升的保障．

[1] 中華人民共和國教育部．義務教育數學課程標準（2011年版）[M]．北京：北京師范大學出版社，2012：2．

[2] 鄭毓信．小學數學教育的理論與實踐——小學數學教學180例[M]．上海：華東師范大學出版社，2017：82．

[3] 崔鈺．關于分數的文獻綜述與教學實踐[J]．北京教育學院學報（自然科學版），2014，9（2）：62–68．

[4] 鞏子坤．理解視閾下的分數除法課程目標的實證研究[J]．教育探索，2010（1）：70–73．

[5] 范文貴，郝翡翠．五年級學生對分數意義的理解[J]．數學教育學報，2017，26（1）：70–75．

[6] 鞏子坤，楊玉東．錯誤僅僅是粗心所致嗎[J]．上海教育科研，2007（9）：90–93．

[7] 趙倩，呂世虎，韓繼偉．中國大陸與臺灣地區小學生數感表現的比較研究——以比較分數的相對大小為例[J]．數學教育學報，2019，28（6）：65–70，91．

[8] 張奠宙，唐彩斌．關于小學“數學本質”的對話[J]．人民教育，2009（2）：48–51．

[9] 章敏．關于分數教學的思考[J]．課程·教材·教法，2015，35（3）：63–67．

[10] 章勤瓊，徐文彬．論小學數學中分數的多層級理解及其教學[J]．課程·教材·教法，2016，36（3）：43–49．

[11] 楊豫暉，宋乃慶．小學五年級“分數的意義”教學結構研究[J]．課程·教材·教法，2010，30（4）：54–57，78．

[12] 華應龍．分數：先分后數——“分數的意義”教學新路徑[J]．人民教育，2011（6）：37–39．

[13] 張丹，孫京紅．整體建構分數意義的教學行動研究[J]．數學教育學報，2015，24（2）：22–25．

[14] 劉加霞．通過“分”與“數（shǔ）”，分數是個“數（shù）”?——兼評華應龍老師執教的“分數的意義”[J]．人民教育，2011（6）：39–42．

[15] 李健，鄭瑩．分數概念的演變及其教學啟示[J]．內江師范學院學報，2018，33（12）：30–35．

[16] 蒲淑萍．“中國美國新加坡”小學數學教材中的“分數定義”[J]．數學教育學報，2013，22（4）：21–24，70．

[17] 吳瓊，高夯．美國、新加坡、中國小學數學教材編寫的指導思想及其特點——基于教師用書的比較分析[J]．外國教育研究，2013，40（9）：120–129．

[18] 丁銳，YAN P X．中美小學數學教材的比較研究——以三年級“分數的認識”為例[J]．數學教育學報，2016，25（3）：20–28．

[19] 楊慧娟，郭蓉蓉，孟夢，等．中韓小學數學教材中分數除法的比較研究[J]．數學教育學報，2020，29（2）：64–69．

[20] 徐亞，隋佳源．小學數學教科書認知復雜程度的比較研究——以中國、日本、新加坡教材的分數問題為例[J]．上海教育科研，2015（12）：37–41．

[21] 張文宇，張守波．海峽兩岸小學數學教材分數內容例題的比較研究[J]．數學教育學報，2015，24（3）：68–72．

[22] 張平，彭亮，徐文彬．大陸與臺灣小學數學教材中分數除法的編排比較[J]．數學教育學報，2018，27（6）：38–43．

[23] 王光明，李健，康玥媛．小學數學教材中分數意義的呈現：歷史順序與“超回歸”倒序的統一[J]．課程·教材·教法，2017，37（5）：34–39．

[24] 陳蓓，章飛．分數意義建構的順序及對教科書設計的建議[J]．數學教育學報，2018，27（4）：58–61．

[25] 蘇洪雨．七年級學生分數學習情況的調查研究[J]．數學教育學報，2007，16（4）：48–51．

[26] 楊伊生，劉儒德．兒童分數概念發展研究綜述[J]．內蒙古師范大學學報（教育科學版），2008（6）：130–134．

[27] 劉春暉，辛自強．分數認知的“整數偏向”研究：理論與方法[J]．心理科學進展，2010，18（1）：65–74．

[28] 張睆，辛自強．分數概念的個體建構——起點與機制及影響因素[J]．數學教育學報，2013，22（1）：27–32．

[29] 張睆，辛自強，陳英和，等．分數概念語義理解對兒童乘法應用題表征的影響[J]．數學教育學報，2017，26（4）：76–79．

[30] 張睆，辛自強，陳英和，等．小學兒童分數概念語義理解水平及模式：基于潛在類別分析[J]．數學教育學報，2018，27（3）：66–71，75．

[31] 韓玉蕾，辛自強，胡清芬．等值分數概念的理解[J]．心理發展與教育，2012，28（2）：210–217．

[32] 辛自強，韓玉蕾．小學低年級兒童的等值分數概念發展及干預[J]．心理學報，2014，46（6）：791–806．

[33] 辛自強，劉國芳．非符號分數與整數計算能力的發展及其與數字記憶的關系[J]．心理科學，2011，34（3）：520–526．

[34] 辛自強，李丹．小學生在非符號材料上的分數表征方式[J]．心理科學，2013，36（2）：364–371．

[35] 孫玉，司繼偉，黃碧娟．分數的數量表征[J]．心理科學進展，2016，24（8）：1?207–1?216．

[36] 高瑞彥，牛美心，楊濤，等．四～八年級學生分數數量表征的準確性及形式[J]．心理發展與教育，2018，34（4）：443–452．

[37] 盧淳，郭紅力，司繼偉，等．不同數字線下兒童與成人分數估計的表征模式[J]．心理發展與教育，2014，30（5）：449–456．

[38] 郭萌，熊妍茜，楊新榮，等．五年級和六年級學生分數表征轉化能力的調查研究[J]．數學教育學報，2016，25（5）：49–54．

[39] 張麗，盧彩芳，楊新榮．三～六年級兒童整數數量表征與分數數量表征的關系[J]．心理發展與教育，2014，30（1）：1–8．

[40] 高婷，劉儒德，劉穎，等．小學生分數比較中的加工模式：基于反應時和口語報告的研究[J]．心理發展與教育，2016，32（4）：463–470．

[41] 李弘祺．學以為己：傳統中國的教育[M]．上海：華東師范大學出版社，2017：605．

[42] KIEREN T E. The rational number construct——Its elements and mechanisms [M] // KIEREN T E. Recent research on number learning. Washington DC: ERIC Publications, 1980: 125–149.

[43] 張奠宙，鞏子坤，任敏龍，等．小學數學教材中的大道理——核心概念的理解與呈現[M]．上海：上海教育出版社，2018：104–106．

[44] 娜仁格日樂，史寧中．度量單位的本質及小學數學教學[J]．數學教育學報，2018，27（6）：13–16．

[45] 倪玉菁．五、六年級小學生對分數的意義和性質的理解[J]．心理發展與教育，1999，15（4）：26–30．

[46] NI Y, ZHOU Y D. Teaching and learning fraction and rational numbers: The origins and implications of whole number bias [J]. Educational Psychologist, 2005, 40 (1): 27–52.

[47] 劉春暉，辛自強．五～八年級學生分數概念的發展[J]．數學教育學報，2010，19（5）：59–63．

[48] SIEGLER R S, THOMPSON C A, SCHNEIDER M. An integrated theory of whole number and fractions development [J]. Cognitive Psychology, 2011, 62 (4): 273–296.

[49] STEFFE L P. A new hypothesis concerning children’s fractional knowledge [J]. The Journal of Mathematical Behavior, 2001, 20 (3): 267–307.

[50] 辛自強，張睆．兒童的分數概念理解的結構及其測量[J]．心理研究，2012，5（1）：13–20．

[51] SIMON M A, PLACA N, AVITZUR A, et al. Promoting a concept of fraction-as-measure: A study of the learning through activity research program [J]. The Journal of Mathematical Behavior, 2018 (52): 122–133.

[52] STAFYLIDOU S, VOSNIADOU S. The development of students’ understanding of the numerical value of fractions [J]. Learning and Instruction, 2004, 14 (5): 503–518.

Teaching and Learning Fractions in Chinese Elementary: A Review of Literature in the Past 30 Years

HUANG Xiao-lin, HUANG Qin-an

(School of Mathematics and Statistics, Shaanxi Normal University, Shaanxi Xi’an 710119, China)

Based on a systemic review of papers involving fractions, there are two main lines of study around the questions of teaching and learning primary school fractions. One focuses on fractions as knowledge and the other pays more attention to knowledge of the cognition around fractions. These lines occasionally intersect, reflecting the effects of traditional education in China—by which teaching and learning activities revolve around teachers—on the study of mathematics teaching. From the perspective of the teaching and learning of fractions, we attempted to explore the feasibility of teaching materials compiled on students’ cognition of fractions and the method of introducing the concept of fractions using the measurement model to show that the concern of education research to students’ learning. We put forward the following viewpoints: based on “learning,” explore mathematical knowledge to enrich knowledge connotation; pay attention to the process of student learning to improve teaching practices; deepen mathematics learning evaluation to promote the cultivation of students’ core literacy; strengthen teachers’ mathematics teaching views to guide their teaching practices; and provide references for mathematics education studies.

the concept of fractions; teaching and learning of fractions; teaching material compiling; measurement model

G622.0

A

1004–9894（2021）06–0039–07

黃曉林，黃秦安．中國三十年來小學階段分數研究文獻的系統分析及啟示[J]．數學教育學報，2021，30（6）：39-45．

2021–08–10

國家哲學社會科學基金2017年度教育學重點招標項目——教師核心素養和能力建設研究（AFA170008）；中央高校基本科研業務費專項資金資助——基于乘法推理教學的小學數學教師數學教育觀念系統研究（2019TS091）

黃曉林（1984—），女，安徽定遠人，博士生，主要從事數學教育與數學教師教育研究．

[責任編校：周學智、陳漢君]