沖擊作用下核用Q390D 鋼的裂紋擴展阻力曲線研究

石媛媛

中廣核工程有限公司，廣東 深圳 518000

結構在裂紋發生與發展過程中始終處于一個較大范圍的屈服狀態。在這種狀態下，大面積的塑性變形在結構斷裂失效之前就已經存在，結構斷裂后，可以看出明顯的頸縮變形。夏比沖擊試驗的加載速率為1 000～100 000 MPa·m/s，是典型的動態試驗，錘頭慣性力會直接影響到試件斷裂。沖擊試驗設備可獲得性強，同時其成本較低、測量時間短、樣品處理方便。這一系列優勢使得這種試驗方法在確定材料脆韌轉變溫度和判斷材料失效特性上具有重要地位，在美國標準中，對不大于16 mm 的鋼板需要采用夏比沖擊試驗進行沖擊韌性進行驗收[1-3]，而且因沖擊試驗便于實現，越來越多的學者紛紛采用這種試驗方法來得到斷裂相關參數。楊承東等[4]利用三點彎試樣的載荷位移曲線計算了A508 鋼材的斷裂韌性，不少學者提出了一系列改進方法，比如修正其加載方式驗證與數據，提高鋼材斷裂韌性的表征準確性，并基于沖擊特征曲線形式與斷口形貌來描述材料的動態斷裂過程。李一磊等[5]對金屬材料夏比沖擊功與裂紋沖擊韌脆關系進行了研究，提出了金屬材料裂紋沖擊韌性評定方法的基本思路。劉志偉等[6]對對鐵素體鋼材Q345B 進行了夏比沖擊試驗，確認了沖擊吸收功的分布規律。李榮德等[7]對鐵素體球墨鑄鐵進行了示波沖擊試驗，確定了溫度對沖擊過程中裂紋形成和裂紋擴展能力的影響。顧浩洋[8]使用示波沖擊試驗測定了Q235B 鋼材的的動態斷裂韌性值JId。何沐陽等[9]利用儀器化夏比V 型缺口沖擊試驗獲得了11MnNiMo 鋼材的沖擊斷裂性能，并確定了起裂時間。本研究通過夏比沖擊試驗得到核用Q390D 鋼的載荷位移曲線，確定了其準確度的起裂點，分別利用準靜態方法、Schindler 法和歸一化方法計算試件的裂紋擴展阻力曲線，并將3 種方法得到的結果進行了對比，分析各自方法的優缺點，為工程實踐提供參考。

1 試驗方法和結果

核用鋼Q390D 是反應堆支承結構的常用鋼材，對其進行加工，得到一個長（L）55 mm、寬（W）10 mm、跨距（S）40 mm、厚（B）10 mm、切口角45°、切口長度2 mm 的夏比沖擊試樣，試樣尺寸示意見圖1，尺寸單位為mm。然后使用INSTRON8801萬能試驗機預制一定長度的疲勞裂紋見圖2，相關參數見表1。

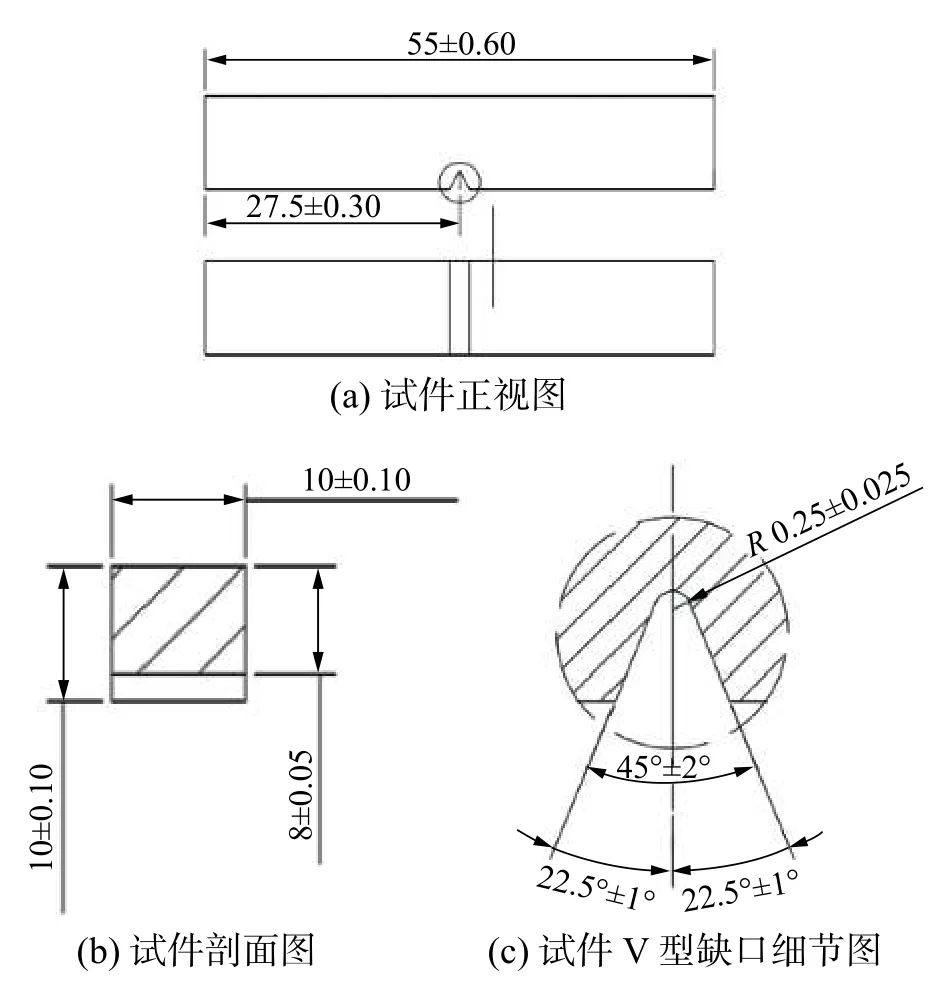
圖1 試樣尺寸示意

圖2 疲勞裂紋試樣加載及裂紋形狀

表1 夏比沖擊試樣預制疲勞裂紋參數

使用德國Zwick 公司生產的ZWICK/ROLL 擺錘沖擊試驗機對含預制裂紋Q390D 試樣進行夏比沖擊試驗，最大的沖擊能量為475 J。具體操作過程參考《GBT229—2007 金屬材料夏比擺錘沖擊試驗方法》[10]。試驗機可以通過安裝在錘頭的傳感器自動記錄沖擊過程中的沖擊載荷，通過軟件可以將數據自動處理為沖擊過程中的載荷-時間曲線，如圖3 和圖4 所示。

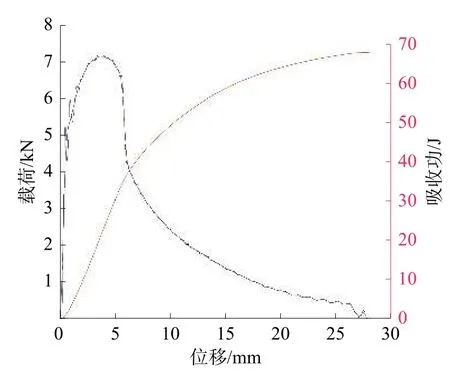
圖3 試樣1 載荷位移曲線

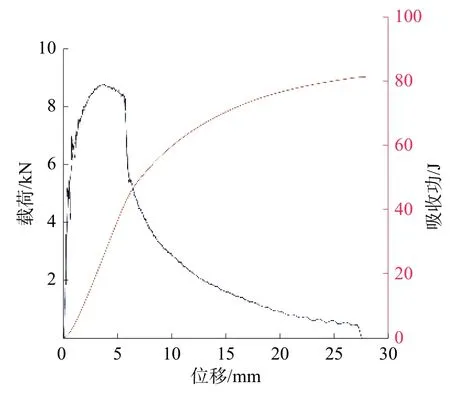
圖4 試樣2 載荷位移曲線

由圖3 和圖4 可以看出，初始階段載荷和位移成線性增加的關系，這一階段，試件處于彈性變形階段；隨后第2 階段載荷的增加趨勢放緩，此時試件處于凈截面屈服狀態；第3 階段載荷和位移呈指數關系提高，此時缺口根部的塑性變形持續提高，最終缺口區域失效，產生細小裂紋；若持續增加載荷到最大載荷，則裂紋會進入到擴展階段，可以看出曲線在緩慢下降一段后出現了載荷陡然下滑的現象，這是由于出現了不穩定裂紋擴展現象；之后曲線又開始了緩慢的下滑直到沖擊試驗結束，這是由于試樣的斷面產生了剪切唇，表明材料的韌性較好。

圖5 為含裂紋Q390D 材料的試樣斷口。通過觀察其斷面樣貌判定為韌性斷裂斷口，整個斷口表面有顯著凹凸，而且在其中間有凹陷情況。在對其斷面形貌進行觀察發現，纖維區主要存在于中間區域，在試樣兩側有明顯的剪切唇產生。

圖5 含預制裂紋Q390D 夏比沖擊試樣的斷口形貌

2 動態裂紋擴展阻力曲線計算

2.1 裂紋起裂點的確定

裂紋的起裂點是作為材料動態斷裂韌性的重要評估依據。雖然基于準靜態加載條件下對于裂紋起裂點的確定方法有很多，但不少方法并不適用動態加載條件，比如電位法是準靜態加載條件下裂紋起裂點的常見測定方法。這種方法是基于裂紋起裂后電位驟變來判斷具體的起裂點位置，但基于動態加載條件下，因測試系統反應時間存在延遲，導致測量數據有滯后性，這大大影響到最終結果的準確性。現階段Kobayashi 等[11]已經引入柔度變化率法作為測定動態加載條件下的裂紋起裂點方法，并且得到學者們的一致認可，尤其是對于擁有良好延性的材料，這種方法往往能夠得出準確度較高的結果。再加上這種方法只用一次試驗即可得出起裂點，因此得到廣泛應用，其數學表達式為

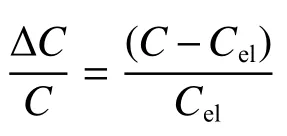
式中：ΔC/C為柔度變化率；C=Δd/ ΔP，為表觀彈性柔度，其中 Δd為位移增量，ΔP為載荷增量；Cel=d/P，為彈性區柔度，其中d為位移，P為載荷。

圖6 為柔度變化率方法原理圖。對于彈性變形區而言，試樣的柔度始終為一定值，有C=Cel，ΔC/C=0；對于塑性變形區而言，ΔC/C持續提高，它的變化率很大程度上取決于材料的加工硬化指數；對于裂紋擴展區而言，因試樣的橫截面面積持續降低，ΔC/C的增長速度更快，因此可以以塑性區和裂紋擴展區間突變點作為起裂點。

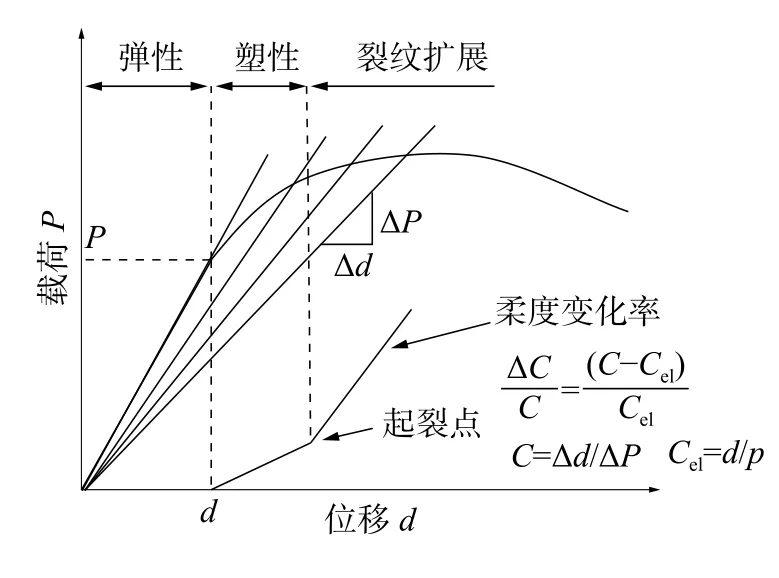
圖6 柔度變化率方法原理

采用柔度變化率法對Q390D 載荷位移數據進行處理，可得到圖7 所示的2 個試件的柔度變化率曲線，相關數據列于表2。

表2 柔度變化率法特征數據

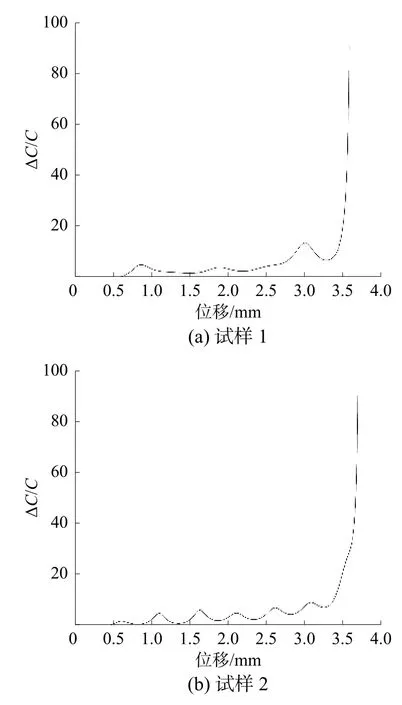
圖7 試樣柔度變化率曲線

通過處理實驗結果可知，當載荷尚未達到最大載荷之前便已經出現了裂紋，而該結論和很多已有研究成果相符[12]，部分學者通過對比分析韌性材料與脆性材料的實驗結果后得出，脆性材料的裂紋產生點多為最大載荷處，但韌性材料的裂紋多產生于最大載荷之前，同時其數據有一定分散性，一般為最大載荷的95%～100%，而相應能量只有最大載荷處能量的八成左右。本次試驗所得結果完全符合統計結果，因此可以說明本次所得起裂點準確無誤。

2.2 準靜態方法求解

學者們在研究中發現，材料動態斷裂韌性屬于加載速率函數[13]，即加載速率變化后材料動態斷裂韌性也會發生變化。因目前加載技術的最大加載速率有限，需要引入不同測試技術來得出不同加載率下的動態斷裂韌性。目前儀器化夏比沖擊試驗最常用的測試加載速率為100 MPa·m/s 量級動態斷裂韌性方法，試樣起裂時間不得小于其與擺錘沖擊系統特征振動周期的3 倍，從而才能保證慣性振蕩衰減充分且不會對后續斷裂發生的識別帶來太大影響，然后將所得結果帶入到準靜態下J積分公式即可。

夏比沖擊試樣的振動周期的計算公式如下：

式中：S、B、W、CLL分別為試樣跨距、厚度、寬度以及柔度，E與c0分別為彈性模量、波速。

本次試樣取S=40 mm，W=10 mm，自振周期計算公式[14]為

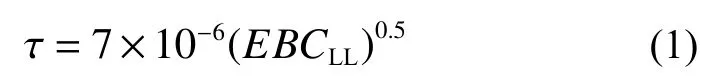
式中EBCLL為試樣的無量綱柔度，表達式為

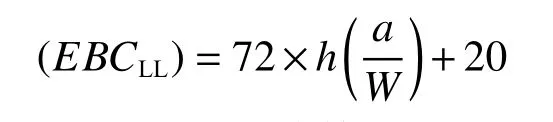
式中h可直接通過式（2）計算得出：

式中a為預制裂紋長度或缺口深度。

把所得h代入到式(1)中即可得出試樣振動周期為0.098 2 ms，引入柔度變化率法可得啟裂時間為0.520 4 ms，因此：

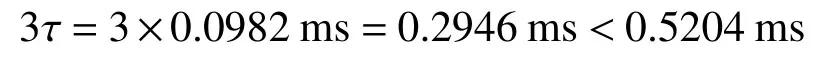
結果顯示3 倍振動周期值比試樣啟裂時間要小得多，這意味著本次實驗得出的結果滿足準靜態條件，可用于材料斷裂韌性公式。

針對裂紋體而言，J積分比應力強度因子K的使用范圍更加廣泛，可直接通過裂紋試件試驗測定得出J積分值[15]，所以本次研究以J積分作為試樣斷裂韌性測試依據。動態J積分是基于動態加載條件下，通過夏比沖擊試驗所得出的第I 類裂紋J積分值，記作JId。根據前文所述，本次試驗不考慮慣性力條件時可視為準靜態，因此有：

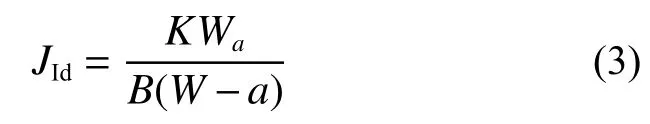
式中：Wa為裂紋長度a對應載荷的沖擊吸收功；K是常數，這里取2。

將前文試驗中得到的裂紋長度和能量值代入式（3）中，可以得到一系列JId的值，將計算得到的JId值畫在坐標軸中，能夠擬合成一條裂紋擴展阻力曲線，如圖8 中紫色曲線所示。

圖8 3 種方法獲得的裂紋擴展阻力曲線

2.3 Schindler 方法求解

目前對于動態加載條件下的阻力曲線測定難度較大，原因在于無法準確繪制出快速斷裂狀態下各時刻的裂紋尖端張開位移，Schindler 等[16]在研究中提出了一種載荷-位移曲線圖，主要用于計算夏比標準試樣受到沖擊后的動態裂紋擴展阻力曲線函數方程，這一方法已經被很多學者證實可行。在使用Schindler 方法時，需要求出沖擊試驗過程中的沖擊總能量Etot和最大載荷處塑性變形能Emp，詳情如圖9 所示。

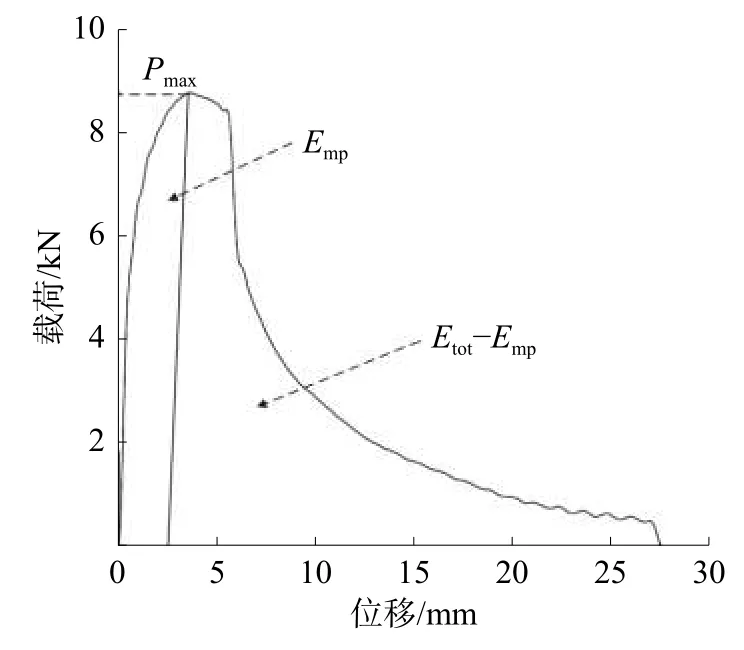
圖9 Schindler 方法能量示意

Schindler 計算動態J-R曲線的表達式為

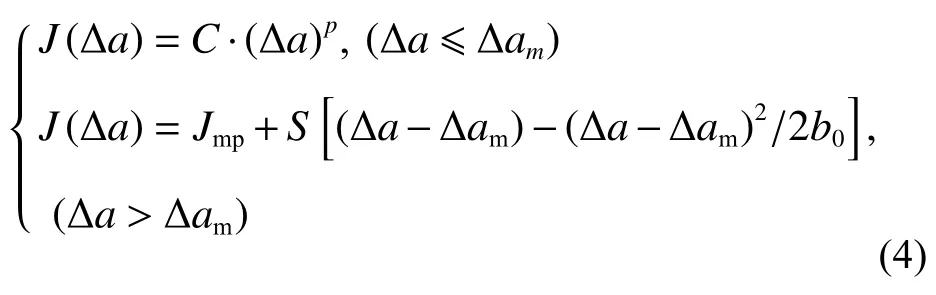
式中：Δa、Δam分別為裂紋擴展量和最大載荷時的裂紋擴展量；a0分別為初始裂紋長度和試樣寬度；b0為初始韌帶寬度，b0=W-a0；C、p、Jmp、s、Δam可由以下計算得到：

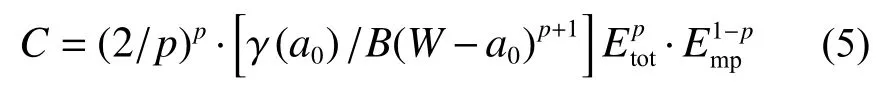
式中 γ為試樣裂紋長度因子[17]，有：

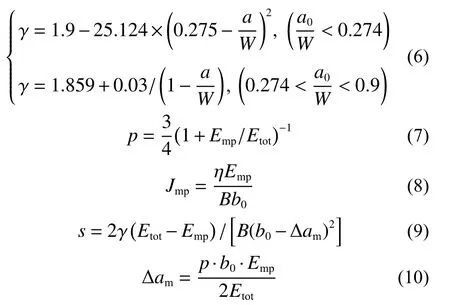
因本次研究中a0/W≈0.4 的試樣1 和試樣2 兩者計算過程完全相同，所以僅對2 號試樣進行計算分析。以試件2 的載荷-位移曲線為例，由式（4）～（10）可以計算出Etot=60.521 J，Emp=20.865 J，p=0.558，Jmp=0.665，C=0.883，Δam=0.585，s=0.501。由以上參數可獲得動態裂紋擴展阻力曲線，如圖8中藍色曲線所示。

2.4 歸一化方法求解

在繪制動態裂紋擴展阻力曲線的過程中，歸一化方法基于試驗所得的載荷位移曲線數據來進行計算，同時考慮了裂紋擴展的修正，所以其所得結果的準確度高。彈塑性J積分可以寫成如下表達式：

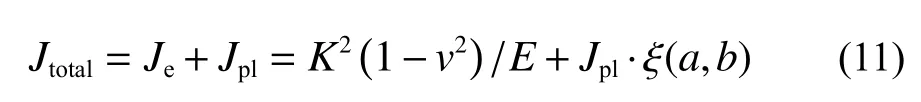
式中：Jtotal為J積分總值，Je、Jpl分別為其彈性與塑性變形部分的J積分值，v為泊松比，K為線彈性應力強度因子，a、b分別為裂紋長度、韌帶長度，ξ(a,b)為裂紋擴展修正因子。塑性變形J積分與裂紋擴展修正的推導如下。

圖10 給出了常規載荷位移曲線圖，圖中有2 條變形路徑：一條是初始裂紋長度a0，另一條是裂紋長度a1。基于塑性形變理論可得出a0對應的J積分值：

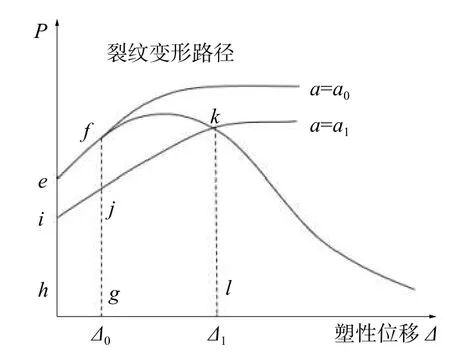
圖10 載荷位移曲線示意

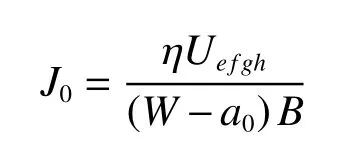
式中：η為塑性因子，Uefgh是ef段載荷位移曲線與坐標軸圍成的面積。

裂紋擴展量為a1時的J積分可以寫成2 部分之和：

當a0與a1之間的差值足夠小時表達式可以改寫成：

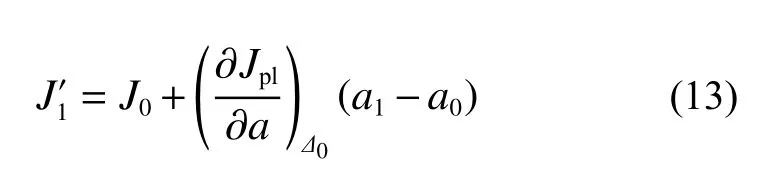
根據塑性形變理論：

將式(15)右端項展開，求解得：

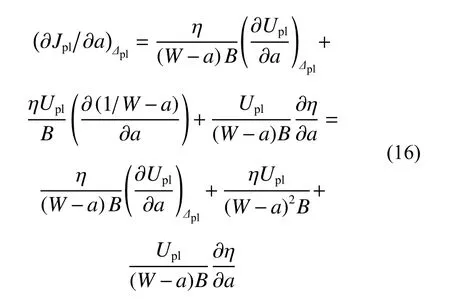
根據J積分形變功率定義[18]，有：

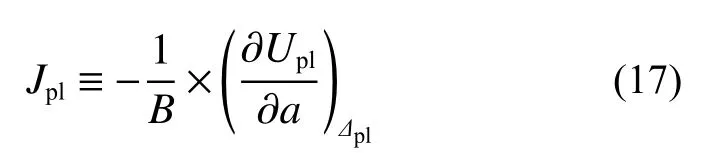
將式(14)、(17)代入式（16），得：

令：

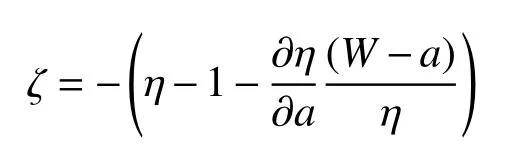
則式（18）可寫成：

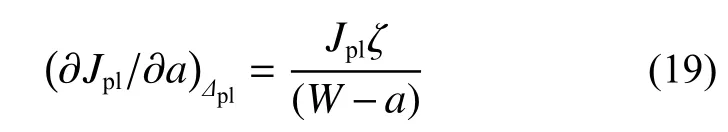
將式(19)代入式（13），得：

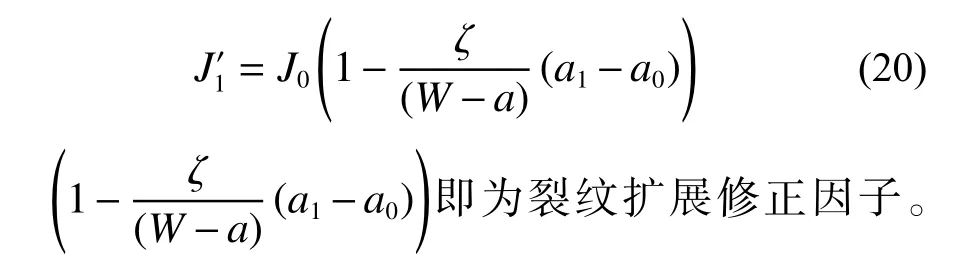
同理得：

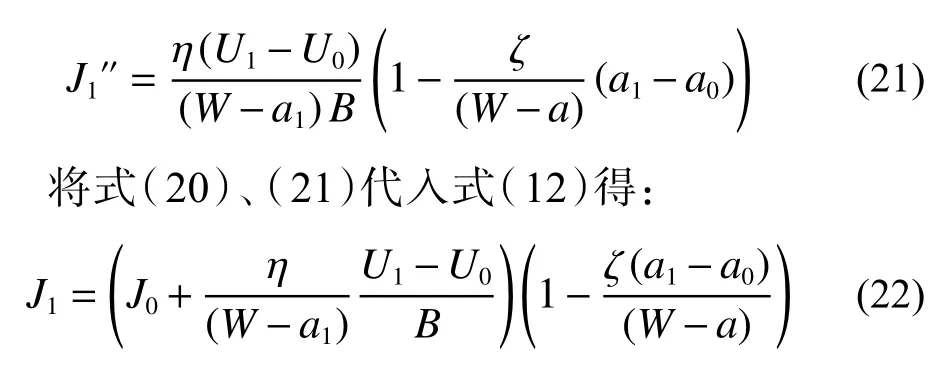
將式（22）寫成增量表達式為

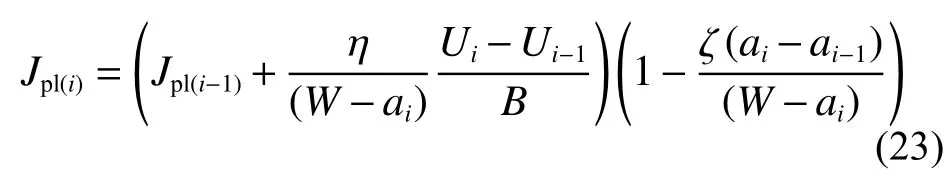
聯合式（11）和式(23)，得積分計算的完整方程表達式為

依據《GBT 38769-2020 金屬材料預裂紋夏比試樣沖擊加載斷裂韌性的測定》[19]，η和 ζ因子可分別取為2 和1。

基于能量吸收角度，Chaouadi 等[20]利用載荷位移曲線計算式（24）中的裂紋擴展量，即

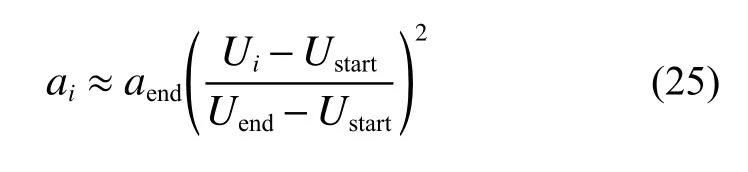
式中：aend為裂紋擴展最終長度，Ustart為起裂時相應的載荷位移曲線面積，Uend為在裂紋擴展階段到最后塑性階段的載荷位移曲線面積。

這樣我們就可以使用式(24)、(25)計算預制裂紋夏比沖擊試樣的動態裂紋擴展阻力曲線。計算得到的動態裂紋擴展阻力曲線如圖10 中紅色曲線所示。

與Schindler 方法計算得到的結果相比較不難看出：當裂紋擴展量達到1.5 mm 前，歸一化方法求得的J積分值大于Schindler 方法求得的J積分值；2 種方法得到的裂紋擴展阻力曲線具有相同的增長趨勢；歸一化方法與Schindler 方法得到的阻力曲線吻合性良好。說明使用歸一化方法求解是可靠的。

大量研究結果顯示，Schindler 方法所得出的結果具有一定的準確度，而且整個計算過程十分簡單。不過這種方法最大的問題在于所獲取的結果過于保守，與實際動態裂紋擴展阻力曲線之間差別較大。總的來說Schindler 方法是利用能量間相互關系，并依托半理論半經驗計算方式來得出裂紋擴展阻力曲線。不過也正是由于有主觀經驗夾雜其中，所以在最終結果的準確度上要略有偏差。當然這種方法能夠迅速繪制出較為準確的裂紋擴展阻力曲線，同時其結果的保守性特征能夠讓其為實踐工程提供一定的指導。而基于載荷位移曲線的歸一化方法對于裂紋擴展阻力曲線的計算將其塑性部分的修正考慮在內，所以這一方法能夠得出更加準確的結果。與其他2 種方法相比，準靜態方法得到的曲線最低，計算結果最為保守。

3 結論

本研究主要通過夏比沖擊試驗得到核用Q390D 鋼夏比沖擊試樣的載荷位移曲線，經過對試驗結果的處理，得到了如下結論：

1）利用柔度變化率方法確定了核用Q390D夏比沖擊試樣的起裂點，結果與同類研究的結果相符，起裂點位于極限沖擊載荷之前，同時柔度變化率曲線振蕩的程度明顯，說明裂紋產生會導致試件力學性能發生劇烈變化，因此使用柔度變化率法來確定核用Q390D 鋼材的起裂點是十分適用的。

2）判斷了準靜態方法的適用性。利用準靜態方法計算了試件斷裂過程中的J積分，通過擬合得到了試件的裂紋擴展阻力曲線。

3）分別使用Schindler 方法和歸一化方法，對含裂紋的核用Q390D 夏比沖擊試樣的裂紋擴展阻力曲線進行求解，結果表明2 種方法所求得的曲線趨勢相同。經過比分析可知，準靜態法由于未考慮動態效應，阻力曲線的計算結果最為保守；Schindler 法與歸一化方法的相對誤差較小，計算過程簡單，適用于工程應用。