含脈沖分數階廣義線性系統的能控能觀性
馮再勇,葉玲華,向崢嶸,謝小韋
(1.南京理工大學自動化學院,江蘇 南京 210094;2.南京鐵道職業技術學院a.基礎部;b.財務處,江蘇 南京 210031)
分數階導數的本質是變量或其整數階導數的弱奇異積分[1-5]。分數階導數定義中的核函數稱為記憶核函數[6-7],它反映了分數階系統的記憶特性。分數階系統適合刻畫具有“過程記憶性”、“歷史遺傳性”等特點的多種物理過程[8-11]。
分數階廣義系統的動態層是用分數階導數刻畫的微分系統,靜態層則是用代數方程描述的代數系統。因此,分數階廣義系統適合于描述狀態變量間既存在分數階微分約束,又存在代數約束的復雜系統[12]。目前學術界對于分數階廣義系統的研究集中于:①探討分數階廣義線性系統的解。如Kaczorek T,Feng Z Y等[13-15]利用分數階廣義線性系統的等價標準型,研究了系統解的存在唯一性等基礎理論及系統求解方法(包括經典解和分布解)。②研究無脈沖分數階廣義線性系統的穩定性、容許性、系統鎮定[12,16-18]等問題。文獻[12]是研究分數階廣義線性系統的奠基性工作,它分別針對導數階數0<α<1和1<α<2兩種情況研究了無脈沖分數階廣義線性系統的穩定性條件。此外,容許性對于廣義系統具有重要意義,其主要特點之一就是系統無脈沖。文獻[16-17]研究了分數階廣義線性系統的容許性條件。文獻[18]基于[17]的工作,研究了導數階數1<α<2時,基于狀態觀測器的容許系統的系統鎮定問題。③關于分數階廣義線性系統的應用研究,典型的應用包括分數階電路系統等[19]。易見,目前關于分數階廣義線性系統的研究,幾乎都是在系統無脈沖的基礎上開展的。
對于分數階廣義線性系統而言,無脈沖要求系統經受限等價變換后,快子系統的系數矩陣N為零矩陣。而更多情況下,特別是一些依據實際問題建立的分數階廣義線性系統模型,系數矩陣N往往不滿足無脈沖條件,此時前述研究結論便不一定適用。
研究控制系統的能控性和能觀性是進行系統控制和設計的基礎,已有關于分數階廣義線性系統完全能控性和能觀性的研究工作包括[24-26],它們都沒有考慮系統含脈沖項的情況。本文基于我們的前期研究結果[20],以系統分布解為基礎,研究含脈沖分數階廣義線性系統的完全能控和完全能觀問題。本文證明了含脈沖分數階廣義線性系統完全能控和能觀的充要條件,給出了判斷含脈沖分數階廣義線性系統完全能控和能觀的秩判據,為關于分數階廣義線性系統的研究、應用提供基礎和依據。
1 分數階廣義線性系統及其能控(觀)性概念
本文討論如下形式的分數階廣義線性定常系統:
(1)
其中t∈T,x(t),y(t),u(t)分別是系統的狀態變量、輸出變量和控制輸入變量。維數分別為x(t)∈Rn,y(t)∈Rm,u(t)∈Rr,系數矩陣E,A∈Rn×n,B∈Rn×r,C∈Rm×n,D∈Rm×r。分數階導數采用Caputo導數,導數階數0<α<1。考慮到系統(1)解的存在唯一性,假設矩陣對(E,A)是正則的,且不要求系統無脈沖。
系數矩陣對(E,A)正則,故存在可逆矩陣P1和P2。對(1)左乘矩陣P1,并令x=P2[x1,x2]T,可將(1)等價地變換為(2):
(2)
其中x1(t)∈Rn1,x2(t)∈Rn2,A1∈Rn1×n1,B1∈Rn1×r,N∈Rn2×n2,B2∈Rn2×r。N是冪零矩陣,設其指數為h,有Nh=0,Ni≠0,i=1,2,…h-1。與一般廣義線性系統相對應,我們稱系統(2.1)和(2.2)分別為系統(2)的慢子系統和快子系統。下面考察系統(2)的狀態響應。
慢子系統(2.1)是分數階線性系統,文獻[15]證明了其狀態響應如下。
引理1[15]慢子系統(2.1)的狀態響應具有如下形式:
(3)
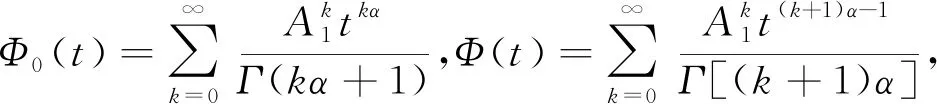

引理2[20]快子系統(2.2)的狀態響應如下:
x2(t,u,x20)=x2i(t,x20)+x2u(t,u)
(4)

(0)]。h是冪零矩陣N的指數,lk=「kα?,k=0,1,…,h-1。
注1引理2中的狀態響應含有脈沖函數及其分數階導數,它是分布解。研究表明,分布解中脈沖函數的分數階導數(即脈沖項)從系統狀態軌跡的角度,刻畫了分數階廣義線性系統的記憶特性。
注2引理2不要求快子系統的系數矩陣N=0,因此它也適用于刻畫含脈沖分數階廣義線性系統的運動分析。
與線性系統的能控性[21-22]概念類似,分數階廣義線性定常系統(1)的完全能控性定義如下:
定義1若對于初始時刻t0∈T的一個非零初始狀態x0,存在一個時刻t1∈T,t1>t0和一個無約束的容許控制u(t),t∈[t0,t1],使系統(1)的狀態由x0轉移到t1時刻時,x(t1)=0則稱此非零狀態x0在時刻t0為能控的。
定義2若狀態空間中的所有非零狀態都在時刻t0,t0∈T為能控的,則稱系統(1)在時刻t0為完全能控的。
考察系統的完全能觀性,一般不考慮系統的控制輸入u(t),但需要結合系統的輸出y(t)進行研究。此時,分數階廣義線性定常系統形式如(5):
(5)
系統(5)經過受限等價變換,可被等價地變換為系統(6):
(6)
其中x1(t)∈Rn1,x2(t)∈Rn2,y1(t)∈Rm,y2(t)∈Rm,A1∈Rn1×n1,C1∈Rm×n1,C2∈Rm×n2。N∈Rn2×n2,是冪零矩陣,設其指數為h,有Nh=0,Ni≠0,i=1,2,…h-1,Caputo導數階數0<α<1。系統(6.1)和(6.2)是系統(6)的慢子系統,系統(6.3)和(6.4)是系統(6)的快子系統,系統輸出為y=y1+y2。
根據線性系統能觀性[21-22]概念,分數階廣義線性系統的能觀性定義如下:
定義3對于分數階廣義線性系統(5)的一個非零初始狀態x(t0)(t0∈T),若存在一個時刻t1∈T,t1>t0使得在觀測時間t∈[t0,t1]內由輸出y(t)能夠唯一確定初始狀態x(t0),則稱此狀態x(t0)是能觀的。
定義4若狀態空間中,所有非零初始狀態x(t0),t0∈T都是能觀的,則稱系統(5)是(狀態)完全能觀的,簡稱能觀的。
2 含脈沖分數階廣義線性系統的能控性研究
含脈沖分數階廣義線性定常系統(2)的慢子系統(2.1)是個一般分數階線性系統。關于分數階線性系統的能控性判定,引理3給出了明確的結論。
引理3[23]分數階廣義線性系統(2)的慢子系統(2.1)完全能控的充要條件是:
(7)
我們重點研究含脈沖分數階廣義線性定常系統(2)的快子系統(2.2)的能控性問題。結合引理2中快子系統(2.2)的分布解,我們給出以下快子系統的能控性判定定理,即定理1:
定理1快子系統(2.2)完全能控的充要條件是:
rankQC2=rank[B2,NB2,…,Nh-1B2]=n2
(8)
即,快子系統的能控性矩陣QC2=[B2,NB2,…,Nh-1B2]行滿秩。
證明根據定義1,即需要證明存在無約束的容許控制輸入u(t)和時刻t,能夠使得系統(2.2)的狀態由x20轉移到原點x(t)=0。由引理2可知,快子系統(2.2)的分布解為:
欲使得x2(t)=0,即要求存在控制輸入u(t)滿足:
(9)
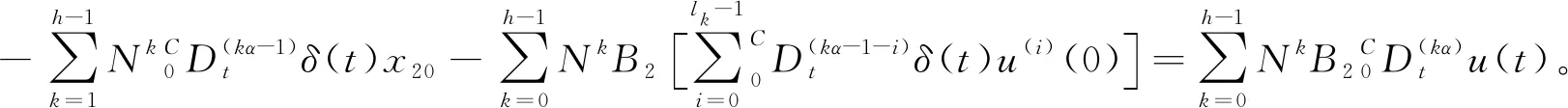
(10)
定理1是判定含脈沖分數階廣義線性系統快子系統完全能控的定理。以此為基礎,我們可以得到更為簡潔的PBH秩判據。
定理2(PBH秩判據)含脈沖分數階廣義線性系統(2)的快子系統(2.2)完全能控的充要條件是:
rank[N,B2]=n2
(11)
證明由線性系統的PBH秩判據可知,定理1的能控性條件,等價于矩陣[λI-N?B2]對于矩陣N的每一個特征值λi都有:rank[λiI-N?B2]=n2。
考慮到冪零矩陣N的特殊結構,可知其特征值λi均等于0,于是定理1的能控性條件等價于:
rank[-N,B2]=rank[N,B2]=n2
證畢!
綜合上述含脈沖分數階廣義線性系統(2)的慢子系統(2.1)和快子系統(2.2)的能控性條件,可得到含脈沖分數階廣義線性系統的能控性判定定理,即定理3。
定理3含脈沖分數階廣義線性定常系統(1)完全能控的充要條件是經受限等價變換后,慢子系統(2.1)和快子系統(2.2)均完全能控,即:
(12)
3 含脈沖分數階廣義線性系統的能觀性研究
含脈沖分數階廣義線性定常系統(6)的慢子系統(6.1)和(6.2),是分數階線性系統。關于分數階線性定常系統的能觀性判定,有如下引理4:
引理4[23]系統(6)的慢子系統(6.1)和(6.2)是完全能觀的充要條件是:
(13)
下面我們以分數階廣義線性系統的分布解為基礎,研究含脈沖分數階廣義線性系統快子系統的能觀性定理,即定理4。
定理4含脈沖分數階廣義線性系統(6)的快子系統(6.3)和(6.4)完全能觀的充要條件是:
(14)
即,快子系統的能觀性矩陣QO2列滿秩。
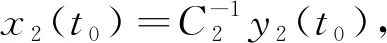
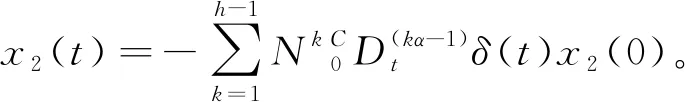
輸出的矩陣形式可以表示為:
(15)
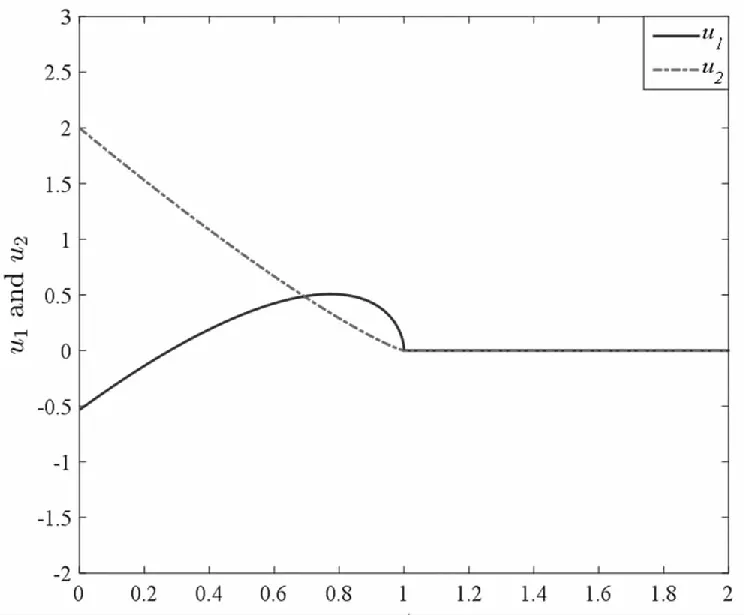
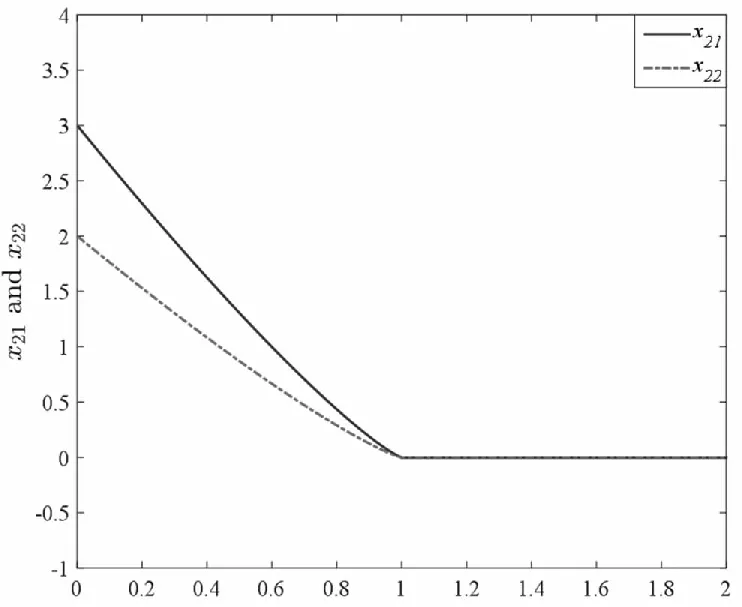
由于m (16) 上式也可以寫成: Y=Mx2(0)=M0QO2x2(0) (17) 欲使(17)具有唯一解,其充要條件是系數矩陣M和增廣矩陣[M?Y]具有相同的秩且秩等于n2,故rankM=rank(M0QO2)=n2。由乘積矩陣秩的性質n2=rankM0QO2≤min(rankM0,rankQO2),可知rankQO2≥n2。又QO2∈Rmh×n2有n2列,故rankQO2≤n2。綜上得到:rankQO2=n2。 證畢! 以此為基礎,我們可以得到快子系統的能觀性PBH秩判據。 定理5(PBH秩判據)含脈沖分數階廣義線性系統(6)的快子系統(6.3)和(6.4)完全能觀的充要條件是: (18) 證畢! 基于上述討論,我們可以得到含脈沖分數階廣義線性定常系統的能觀性判定定理,即定理6。 定理6含脈沖分數階廣義線性系統(5)完全能觀的充要條件是經受限等價變換后,慢子系統(6.1)~(6.2)和快子系統(6.3)~(6.4)均完全能觀,即: (19) 我們可選擇適合的控制輸入u1,u2,讓這兩個狀態變量在有限時間內趨向于0。比如,取分段連續的控制輸入: t/s圖1 導數階數為0.6時的u1,u2 t/s圖2 導數階數為0.6時的x21,x22 t/s圖3 導數階數為0.2時的u1,u2 t/s圖4 導數階數為0.2時的x21,x22 針對含脈沖分數階廣義線性系統,本文以受限等價變換為工具,結合分數階廣義線性系統含脈沖項的分布解,證明了含脈沖分數階廣義線性系統的完全能控性和完全能觀性定理,并給出了簡便實用的含脈沖分數階廣義線性系統的能控性和能觀性秩判據。算例說明,本文所提出的含脈沖分數階廣義線性系統的完全能控(觀)定理和判據便捷有效。此外,我們知道,對偶線性系統的能控性和能觀性之間滿足對偶原理。含脈沖分數階廣義線性系統的對偶系統的形式和結構如何,對偶原理是否仍然成立值得在后繼工作中加以研究。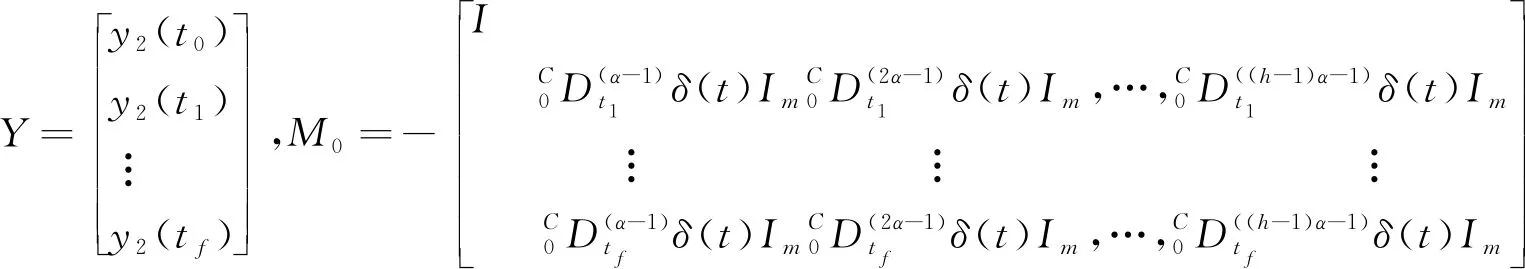
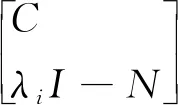
4 相關算例
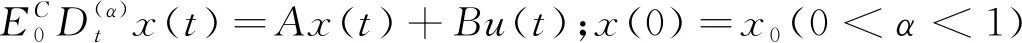
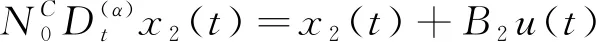
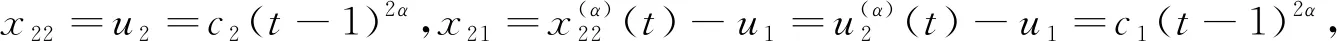
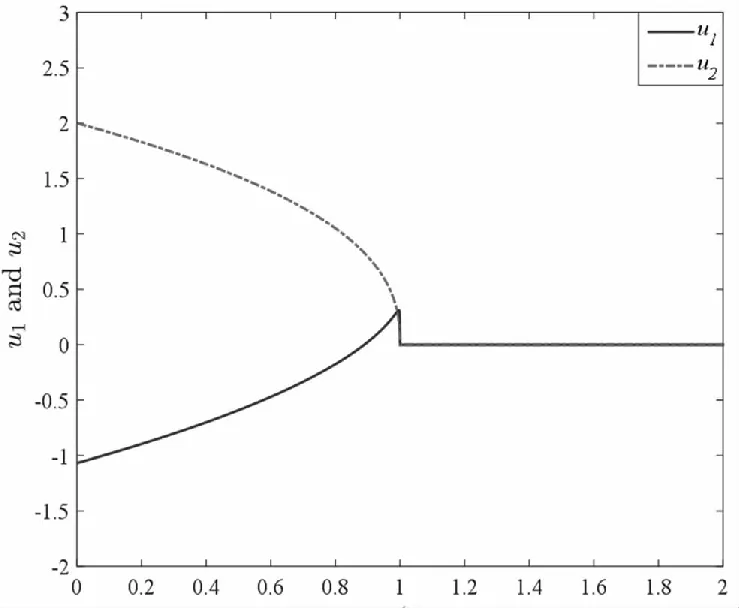
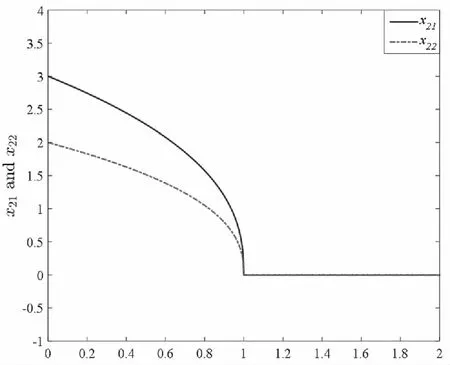
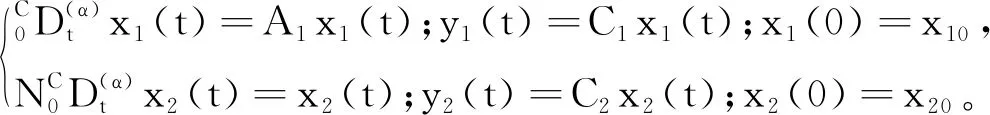
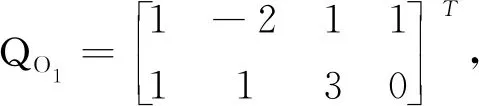
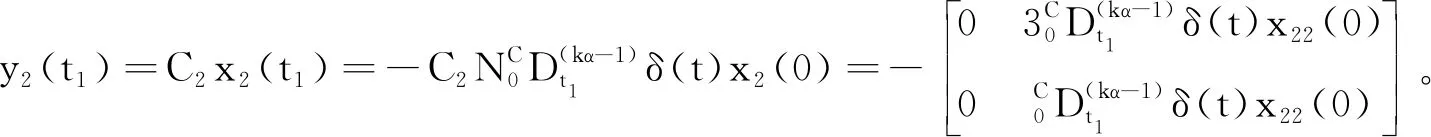
5 結論

