礦物浮選動力學模型及影響因素研究進展
馬 強 李 育 彪 李 萬 青 向 焱 李 詩 浩
(武漢理工大學資源與環境工程學院,湖北 武漢 430070)
泡沫浮選是一種以目的礦物附著于氣泡為基礎的物理化學分離過程[1]。由于目的組分礦物的累計回收率隨浮選時間的增加而增加,本質上可將浮選過程看作一個時間-回收率過程[2-5]。浮選動力學可用來描述回收率隨時間變化的過程,并通過分析礦物浮選速率的變化規律來研究各因素對浮選過程的影響。
眾多學者對浮選動力學模型及其改良開展了相關研究工作,使其更加適用于浮選體系。如確定浮選動力學反應級數n;通過劃分浮選組分強化動力學模型的適應性;探究引入參數對浮選速率常數k的影響規律;賦予不同k值來劃分浮選組分等。以上研究推動了浮選動力學模型的快速發展,但學者們更多地研究浮選過程中各因素對浮選動力學的影響,即通過浮選動力學來量化各因素對浮選的影響,從而對現有工藝進行優化[2-8]。
為了總結浮選動力學的研究進展,本文概述了浮選動力學基本模型、發展歷程及研究現狀,并著重對其影響因素開展了討論。
1 浮選動力學基本模型及發展歷程
1.1 浮選動力學基本模型
浮選數學模型的構建往往決定于模型的用途,一般可分為經驗模型、概率模型及動力學模型[2-3,9-10],其中,經驗模型的建立對相應條件要求過于具體,一般通過嘗試及錯誤反饋進行優化;概率模型在某些條件約束下可簡化為動力學模型[3];而動力學模型主要來源于浮選動力學理論。20世紀30年代,ZUNIGA等[11]最先提出浮選動力學模型,把浮選過程近似看作一個速率過程,認為氣泡與礦物顆粒的碰撞、吸附和化學反應中基本物質單元(分子、原子及離子)的作用方式一致,浮選過程中槽內目的礦物與浮選時間呈指數關系。因此,可將一級化學反應動力學模型作為浮選動力學模型。一級化學反應動力學模型為

式中:c0代表目的組分初始濃度,mg/L;c代表t時刻的目的組分濃度,mg/L;k代表反應速率常數。
進一步推導可得經典一級浮選動力學模型
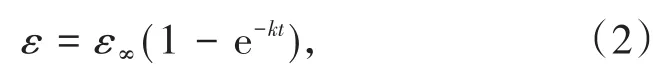
式中:ε∞代表最大回收率,%;ε代表t時刻可浮礦物回收率,%;k代表浮選速率常數。
1.2 浮選動力學模型發展歷程
經典一級動力學模型的建立極大地促進了浮選動力學的發展,但實際應用中,有學者把所得結果按lg(1/(1-R))-t畫圖,發現某些試驗點明顯呈非線性分布,與一級動力學模型不符[12]。于是,人們試圖將一級動力學模型擴展為n級動力學模型來解釋這種非線性浮選過程。1950 年,ARBITER[13]首次提出浮選速率正比于目的礦物濃度的2次方。由此,浮選動力學研究傾向于級數n的確定。后來,在二級浮選動力學模型基礎上,PLAKSIN和KRASIN提出了更符合實際的n級浮選動力學模型,即

式(3)中,n為反應級數(0 在實際應用中,礦漿各組分并不是一個整體,礦漿中存在體積不均勻性。1962年,ARBITER及HARRIS[14]最先提出浮選過程中的兩相模型。之后,很多研究對浮選的不均一性進行了深入研究,在兩相基礎上提出了三相、四相模型[12]。盡管多相浮選動力學模型對所浮礦物的不均一性進行了較好描述,但浮選回收率與時間并非線性相關,即k值不恒定。1963年,今泉常正[15]最先提出同種礦物具有不同k值分布,首次對ε-t呈非線性關系進行了解釋。隨后,人們的研究側重于浮選速率常數k值的確定。1965年,WOODBURN[16]提出浮選速率常數k值服從Γ函數分布 包括均勻分布、快慢浮兩點分布、多項式分布,即F(k)=a+bk+ck2+dk3均屬于k值分布;后來有學者提出k值服從β函數分布 這可歸類于k值隨時間變化。 在此研究基礎上,許多學者根據浮選流程、礦石性質推導出了不同的浮選動力學模型,包括經典一級動力學[11]、一級矩形分布[17]、二級動力學[13]、二級矩形分布[18]、陳子鳴[19]、劉逸超[20]、許長連[21]、哥利科夫[19]及吳亦瑞三重逼近[22]等模型。 浮選動力學模型中,以經典一級動力學模型n應用最為廣泛。為使其更加適用于實際浮選,眾多學者開展了k值分布密度函數、k值的組成及變化規律等方面的研究工作,進一步提高了擬合精度。如于洋等[23]對黑鎢礦、白鎢礦及螢石的浮選分離過程進行了浮選動力學研究,發現浮選速率常數k值持續變化,檸檬酸為抑制劑能顯著擴大三者的浮選速率差異,在經典一級動力學模型基礎上得到優化后的分速模型 式中,f和s分別代表快浮和慢浮;ε∞代表最高回收率,%;ε代表累計回收率,%。修正后的模型精度得到了顯著提高。AI等[24]為了研究細粒黑鎢礦的浮選特性及其浮選動力學,在經典一級模型基礎上提出了新模型,即 式中:ε1∞及k1分別為易浮黑鎢礦的最大回收率及浮選速率常數,ε2∞和k2分別為難浮黑鎢礦的最大回收率及浮選速率常數。通過與經典一級模型、修正一級模型、矩形分布一級模型及二級模型對比,可知新模型對細粒黑鎢礦具有最好的擬合效果。 在實際礦物浮選過程中,一方面可通過浮選動力學模型從微觀層面闡述目的礦物浮選特性,另一方面又可以根據浮選動力學結果評價浮選藥劑作用效果。金會心等[25]在研究富稀土磷礦的浮選動力學變化規律時引入了時間滯后因子θ,對經典一級動力學模型進行修正,從而推導出富稀土磷礦反浮選動力學速率模型,即 對該模型結果進行方差分析,可知捕收劑WF-01用量對修正速率常數kmod影響最大,抑制劑H3PO4用量對選擇性指數SI影響最大。 為了更直觀對比并優化不同模型,CHEN等[26]對長焰煤氣泡浮選與油泡浮選動力學進行了研究,并對6種動力學模型同時進行了優化。結果表明:采用油泡浮選相較氣泡浮選更容易在前中期提高精煤產率,相比于其他模型,經典一級動力學模型能較好地描述氣泡浮選,但6種模型對油泡浮選結果擬合偏差都較大。為了更好地描述油泡浮選,在浮選動力學模型中減去時間常數t,即可平衡油氣泡浮選延遲,提升了擬合精度。6種改進的模型中,經典一級模型最適合描述油泡浮選過程。 為了擴展經典一級動力學模型的通用性及可行性,使之能在廣泛條件下描述浮選過程,KLIM?PELR[17]提出了一級矩形分布浮選動力學模型。BAYAT等[27]在研究粒度分布對土耳其閃鋅礦浮選行為的影響時,發現d80=0.125 mm進料粒度下的浮選行為與一級矩形分布模型相吻合,適應性最好。 目前,一級浮選動力學模型的研究主要集中在提高模型的適用性及擬合精度,通過劃分不同浮選組分、引入不同參數等手段不斷對模型進行優化,使其更符合實際浮選規律,擴大模型適應面。盡管針對一級動力學模型的優化已經開展了不少研究工作,但模型所適應的礦石類別仍具有一定局限性,相關系統性研究工作還有待加強。 當浮選動力學模型中的級數n取2或3時,可分別得到二、三級浮選動力學模型。相較于一級浮選動力學模型,多級浮選動力學模型考慮到礦物類型、礦漿密度、礦漿pH、藥劑添加量及充氣量等的影響,能夠更好地描述浮選過程。LIAO等[28]以低階煤為目的礦物,采用氣泡浮選和油泡浮選對其浮選特性及浮選動力學進行了研究,擬合結果表明低階煤在2種浮選法中均可用二級浮選動力學模型描述。為了更廣泛地表示浮選速率常數k的分布,KLIMPEL[18]提出了二級矩形分布浮選動力學模型,SALEHA[29]的研究結果表明二級矩形分布浮選動力學模型能較好地描述鐵礦石浮選結果。 為使所得浮選數據按lg(1/(1-R))-t作圖呈線性分布,VOLKOYAZ[30]提出了三級浮選動力學模型。在實際應用中,針對礦物顆粒被捕獲時上升速度不同,采用三級浮選動力學模型可對慢浮礦物浮選特性進行描述。羅成等[31]以窄粒級煤泥為浮選對象,進行了反應級數n的研究。結果表明:浮選初期,當n分別取1、2、3時,浮選動力學模型均與實際浮選數據吻合。浮選后期,只有一級動力學模型與實際吻合,二、三級浮選動力學模型擬合值均偏小。這歸因于一級浮選動力學收斂速度更快,隨著反應級數n取值增大,模型收斂速度越慢,而煤泥上浮速度較快,使二、三級浮選動力學不能很好描述煤泥浮選過程。因此,二、三級浮選動力學模型更適用于慢浮礦物。 為增強浮選動力學模型對實際浮選過程的適應性,BROZEK[32]提出了非整數級浮選動力學模型,即 BU等[33]對某煤泥特定粒級(-188μm和-100μm)進行了擬合,發現非整數級浮選動力學模型能更好地描述浮選過程。 針對浮選動力學模型的研究表明,現階段浮選動力學模型的發展建立在經典一級浮選動力學模型基礎上,大致分為兩個方向:①針對實際礦石性質引入不同參數,或對浮選組分進行細分,得到不同組分的浮選速率常數;②通過試驗驗證以確定模型反應級數n,得到與之對應的最佳取值,提高模型擬合精度。 浮選動力學模型在經典一級動力學模型的基礎上得到了較大發展,增強了浮選動力學模型對復雜礦物的適應性。但是浮選過程復雜,包括礦粒和氣泡的相互接觸、疏水礦粒在氣泡上粘附形成礦化氣泡、礦化氣泡進入泡沫層及精礦泡沫層的排出[34]。在這些浮選過程中,礦物顆粒自身性質(如礦物晶體結構、顆粒大小及形狀)、浮選工藝參數(如浮選藥劑種類及用量)及浮選機結構參數等均可對其產生影響[2,4,6,9,35-36],總結各個因素對浮選動力學模型的影響對優化模型的適應性具有重要意義。 礦物晶體結構對浮選特性有很大影響,如晶胞原子缺失、晶型轉變及晶格膨脹均會影響礦物的晶體結構,從而導致晶胞周期性勢場、電子分布以及能帶結構的改變[37],并最終影響礦物浮游性能[38-39]。SALMANI等[40]研究了晶體溶解對浮選動力學的影響,結果表明,溶解會導致脈石礦物表面晶格定位離子減少,伴生脈石礦物浮選速率常數顯著減小。 同樣,礦物粒度對浮選動力學各參數影響顯著,ABKHOSHK[41]在間歇浮選槽中運用非線性方程對浮選速率常數與煤粒度的關系進行了量化,方差分析結果表明,相比最大理論回收率,粒度對浮選速率常數影響更大;模糊模型計算結果顯示,粒度大小、浮選時間及累計回收率的3D模型可對不同粒度煤的累計回收率進行預測。ZHANG等[2]研究了粒度對褐煤反浮選動力學的影響,運用1stOpt軟件對試驗結果進行6種模型擬合并預測浮選速率常數、最大灰分回收率與粒度的關系。結果表明:除經典一級動力學模型外,其他模型均能很好地擬合不同粒級的試驗數據。當粒級為150~250μm時浮選速度常數最大,這可能是由于浮選中碰撞、附著及分離等關鍵步驟決定,由于顆粒較高的脫附率,在此過程中細粒級礦物與氣泡碰撞概率較低、粗粒級礦物浮選速率低。通過反浮選效率指數對褐煤的反浮選效果與粒度的關系作了進一步評價,發現在給定時間內,與所研究的窄粒級組分相比,褐煤粒級為-425μm時反浮選動力學參數最佳。YALCIN等[42]對黃鐵礦型金礦浮選動力學進行了研究,結果表明:金對應浮選速率常數與粒度呈負相關;相比一級模型,采用二級模型時,浮選速率常數對磨礦粒度有著更高的依賴性,相關系數均大于0.998。 礦物顆粒延伸率、圓度及形狀特征影響其與氣泡的相互作用,進而影響礦物浮選分離效率[43-44]。DEHGHANIF等[45]研究了顆粒形狀對磁鐵礦單礦物浮選動力學的影響,發現具有較高延伸率和較低圓度的顆粒具有較大的浮選動力學常數。此外,有石英顆粒存在時,磁鐵礦顆粒形狀對浮選影響更大,浮選動力學常數也比單獨浮選磁鐵礦時高。MA等[46]采用6種浮選動力學模型研究了焦煤顆粒形狀對浮選動力學的影響,結果同樣表明:由于顆粒與氣泡之間的作用面積增大,顆粒延伸率與可浮性呈正相關,且焦煤浮選符合一級矩形分布浮選動力學模型。RAHIMI等[47]研究了不同研磨方法對石英顆粒形狀及浮選的影響,結果表明:石英顆粒形狀顯著影響浮選速率常數,較高延伸率及低圓度顆粒具有較高可浮性。 浮選過程中除了礦物本身性質的影響,浮選藥劑也起極其重要的影響[48]。NATARAJAN等[49]研究了N-芳香異羥肟酸不同取代基對加拿大某鎳礦浮選動力學的影響。結果表明,相比黃藥,N-苯基-N-(2,6二甲基苯基)羥胺浮選鎳黃鐵礦時具有更好選擇性及較高的一級浮選動力學速率常數。KLIMPEL[50]研究了烴鏈長度對各種硫烴捕收劑性能的影響。結果表明:與傳統水溶性捕收劑相比,硫烴捕收劑可降低藥劑成本,增大浮選速率常數,提高對硫化鐵的選擇性。ZHU等[5]通過咪唑離子液體(1-烷基-3-甲基咪唑氯化物)配制微乳液浮選煤泥,所得煤泥的可燃體回收率及凈灰分含量與正十二烷浮選效果類似,不但節省捕收劑約43%,且無需起泡劑,是煤泥浮選的高效捕收劑,浮選過程符合一級矩陣分布模型。張晉霞等[51]對石英、藍晶石和黑云母在pH=6.5時的浮選動力學進行了研究。結果表明,抑制劑淀粉可擴大3種礦物浮選速率差異,模型擬合發現經典一級動力學模型與實際數據相吻合。 常用的浮選機有機械式浮選機、浮選柱及反應器、分離器式浮選機[52-53],其類別、葉輪傾角及轉速、充氣量等都會影響氣泡與礦粒的相互作用,進而影響浮選動力學。 GAO等[54]研究了操作參數對BF-40浮選機浮選動力學的影響,對比分析3種不同葉輪轉速和浸入深度,發現主軸轉速為151 r/min、葉輪浸入深度1 195 mm時,BF-40型機械攪拌浮選機能獲得最佳浮選動力學參數。 KOH等[55]通過CFD方法研究了Denver自充氣式浮選機葉輪轉速對氣流的影響,并進行了浮選動力學模擬。研究發現:空氣通過葉輪的旋轉作用進入礦漿,空氣流速由葉輪產生的吸入壓力及進氣閥到葉輪輸送軸上的摩擦損失共同決定。浮選動力學模擬表明:重力作用對顆粒附著影響顯著,可通過控制葉輪轉速調節氣泡上升速度達到提高浮選速率的目的。KOH等[56]進一步通過CFD計算模型模擬自充氣式浮選機槽內多尺寸氣泡與顆粒的附著速率。結果表明:氣泡分布對顆粒浮選速率影響顯著,全尺寸氣泡分布的浮選速率高于單尺寸氣泡的浮選速率,更有利于優化浮選槽設計,提升浮選槽工作效率。韓偉[57]針對JFC-150型浮選機內流特性,研究了浮選機充氣量、礦漿含氣量及氣泡礦化概率等對浮選動力學參數的影響。結果表明:較高的葉輪轉速和較大的充氣壓力會增強分離區及輸運區的湍流強度,從而增大顆粒懸浮能力及脫附作用力,最佳葉輪轉速為110~130 r/min、充氣壓力為50~60 kPa。 LI等[58]研究了充氣式旋流浮選柱充氣量對不同粒徑組分浮選特性的影響,并在此基礎上提出了一種新的浮選動力學模型。結果表明:充氣量的增加能顯著提高粗、細煤泥浮選回收率,特別是粗煤泥的分選。對于0.25~0.50 mm的粗粒級,新模型中煤泥R2值(相關系數)接近1,SSE(誤差平方和)接近0,表明該粒級浮選與新模型吻合。 張曉燕[59]采用類似于浮選柱的自制攪拌式浮選槽研究了葉輪轉速對煤泥浮選動力學的影響。結果表明:提高葉輪轉速可提高精煤產率及可燃體回收率。由模型擬合可知煤泥浮選符合一級動力學模型,過高轉速會降低k值。因此,葉輪轉速不宜過高。葉輪低轉速時,不同密度細煤泥對應的k值差異較大,對于高、低密度級煤泥,葉輪轉速分別為600 r/min、800 r/min時可獲得最佳浮選動力學常數。 FILIPPOV等[60]對在反應器、分離器中黃銅礦、石英混合礦浮選動力學進行了研究。結果表明:采用反應器、分離器有助于黃銅粗精礦浮選回收率的提高,增大其浮選速率,這是因為反應器/分離器存在不同的區域,可將氣流分散到氣泡中,增強氣泡與顆粒的附著。 除了上述浮選設備外,有學者研究了新型振蕩網格浮選槽(OGC)對浮選動力學的影響。CHANGUNDA等[61]以甲基化石英為研究對象,對OGC能量輸入引起浮選動力學的變化進行了研究。結果表明,浮選速率常數隨功率強度的增加呈近似線性關系,可能是由于輸入的能量在湍流環境中較好地促進顆粒-氣泡接觸。田全志等[62]以低階煤為研究對象,對能量輸入引起的可浮性進行了研究。結果表明:低能量輸入不利于增加氣泡與礦粒的碰撞吸附概率,高能量輸入易夾帶高灰細泥。因此,輸入中等能量能夠促進低階煤浮選,符合一級矩陣模型,而高能量輸入時則符合經典一級模型。 除了礦物粒徑和形狀、藥劑、浮選設備等參數影響浮選動力學外,礦漿濃度、泡沫滯留時間、超聲波處理及研磨介質種類等都可對礦物浮選動力學產生影響。 繆亞兵等[63]研究了螢石礦漿質量濃度對浮選動力學的影響。結果表明:增大螢石礦漿濃度能夠增大浮選速率常數。鄭雪華[64]研究了浮選過程中泡沫滯留時間對浮選速率常數k值的影響。結果表明:浮選速率常數k隨泡沫滯留時間呈指數式減小。 MAO等[65]研究了高灰分褐煤浮選特性,包括超聲礦漿層、泡沫層對褐煤浮選動力學的影響。結果表明:常規浮選及超聲礦漿層、泡沫層浮選對應浮選動力學速率常數k分別為2.313 3、0.837 3和4.211 4,且泡沫層超聲處理時可浮性差的褐煤浮選符合二級矩形分布模型。因此,在泡沫層超聲能夠顯著增大浮選速率常數k,為褐煤超聲浮選提供指導依據。 為了解釋磨礦介質種類對礦物浮選動力學的影響,ZHANG等[66]研究了不同磨礦介質對黃鐵礦浮選動力學的影響。結果表明:陶瓷球研磨黃鐵礦時,分散在黃鐵礦表面的鐵氧絡合物較少,可明顯增加黃鐵礦浮選累計回收率。模型擬合結果表明:以陶瓷球為研磨介質時,浮選過程符合一級動力學,而以鑄鐵球為研磨介質時,一級、二級動力學模型均與結果相吻合。由此可知,不同磨礦介質造成鐵氧絡合物含量差異,影響黃鐵礦浮選動力學,其中采用陶瓷球作為研磨介質能較好地提高黃鐵礦浮選效率。 總結可知,不同因素往往可通過3個方面影響礦物浮選動力學:①改變礦物晶體結構;②影響礦物顆粒與氣泡間的粘附概率;③改變礦物表面親、疏水性。 礦物浮選動力學的影響因素涉及礦物晶體結構、形狀和表觀形貌、藥劑種類、浮選設備及實驗過程中各種參數的變化。為了優化浮選工藝流程、改造工藝設備并提升浮選過程中智能化控制,研究工作者開展了大量的科學研究。當前浮選動力學主要從模型參數的引入或浮選組分的劃分、n值的確定兩大方向發展。但是,浮選動力學模型發展存在兩方面的不足,其一為現階段浮選動力學模型更適用于一元礦物的浮選過程,對多元礦物分選難以很好地進行描述;其二,在實際浮選中,影響礦物浮選動力學模型的因素不是單獨存在,而現階段浮選動力學模型的建立與優化并不能統籌以上各因素。 鑒于此,為了不斷優化浮選動力學模型來更好地描述浮選過程,通過計算機強大的分析處理能力,運用理論計算對影響浮選動力學的各因素進行評估,并結合工藝礦物學、浮選機內礦漿的流體運動規律來加強浮選動力學模型對不同礦物、不同因素下浮選過程的適應性,是未來需要重點關注的研究方向。此外,基于浮選動力學分析對浮選設備進行優化,有利于提高礦物浮選分離效率,具有重要現實及科學意義。

2 浮選動力學模型研究現狀
2.1 n=1的浮選動力學模型
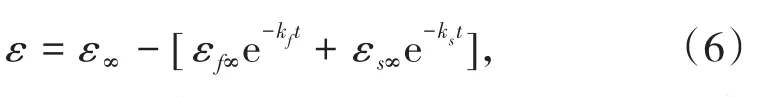


2.2 n>1的浮選動力學模型
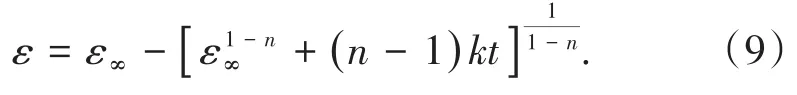
3 浮選動力學模型的影響因素
3.1 礦物顆粒自身性質的影響
3.2 浮選工藝參數的影響
3.3 浮選設備的影響
3.4 其他因素的影響
4 結論與展望

