方鋼管超高性能混凝土組合墩柱抗震性能仿真分析*

郭啟文 劉世忠 栗振鋒 趙曉晉 董奎吾 趙明偉

(1.太原科技大學(xué)交通與物流學(xué)院 太原 030024；2.山西省交通科技研發(fā)有限公司橋梁工程防災(zāi)減災(zāi)山西省重點(diǎn)實(shí)驗(yàn)室 太原 030006)

鋼管混凝土組合墩柱以其承載力高、延性好、抗震性能好、施工方便等優(yōu)點(diǎn)日益受到工程界的重視。近年來(lái)，隨著橋梁跨徑的增大、車輛載重的提升，普通鋼管混凝土組合墩柱已無(wú)法很好地滿足橋梁承載力與抗震能力的要求[1]。超高性能混凝土(ultra-high performance concrete，UHPC)作為一種新型材料，其具有超高強(qiáng)度、超高韌性等力學(xué)特性[2]，將UHPC材料填充至鋼管中，較普通鋼管混凝土組合墩柱有更加優(yōu)良的力學(xué)性能。

近年來(lái)，眾多學(xué)者通過試驗(yàn)和數(shù)值分析對(duì)組合墩柱的抗震性能進(jìn)行了大量研究。韓林海等[3]對(duì)30個(gè)矩形鋼管混凝土構(gòu)件進(jìn)行抗震性能試驗(yàn)研究，并用數(shù)值方法分析了構(gòu)件高寬比、鋼材屈服強(qiáng)度等參數(shù)對(duì)抗震性能的影響。李兵等[4]對(duì)方鋼管混凝土柱進(jìn)行有限元仿真，探討了截面含鋼率、長(zhǎng)細(xì)比等因素對(duì)試件水平承載力的影響。孫曉嶺等[5]對(duì)高寬比為3的薄壁鋼管混凝土柱進(jìn)行抗震試驗(yàn)研究，將軸壓比作為影響參數(shù)，研究其對(duì)薄壁鋼管混凝土柱滯回行為及耗能能力的影響。吳誠(chéng)等[6]設(shè)計(jì)了4根方鋼管超高混凝土短柱，主要研究了軸壓比、含鋼率等參數(shù)對(duì)其抗震性能的影響。張西丁[7]運(yùn)用有限元軟件探討了墩柱不同直徑、墩柱截面形狀對(duì)橋梁抗震性能的影響。以往的研究中，國(guó)內(nèi)學(xué)者主要針對(duì)普通強(qiáng)度等級(jí)混凝土、高強(qiáng)度等級(jí)混凝土填充的鋼管組合墩柱進(jìn)行研究，而對(duì)以超高性能混凝土為核心的鋼管組合墩柱研究較少。因此，研究以超高性能混凝土為核心的鋼管組合墩柱的抗震性能具有重要意義，可為工程施工及設(shè)計(jì)提供一定的參考。

本文利用大型有限元軟件ABAQUS對(duì)方鋼管UHPC組合墩柱進(jìn)行參數(shù)化建模，以軸壓比、長(zhǎng)細(xì)比與套箍系數(shù)為影響參數(shù)設(shè)計(jì)對(duì)照組，分析不同參數(shù)對(duì)組合墩柱滯回曲線、骨架曲線、延性系數(shù)與耗能能力等抗震性能的影響。

1 方鋼管UHPC組合墩柱

本文以方鋼管UHPC組合墩柱為研究對(duì)象，UHPC組合墩柱由外套鋼管、內(nèi)填UHPC、內(nèi)置鋼筋三部分組成。方鋼管UHPC組合墩柱構(gòu)造示意圖見圖1。

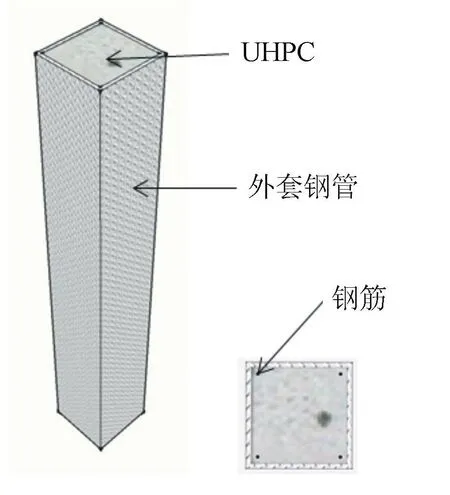
圖1 方鋼管UHPC組合墩柱構(gòu)造示意圖

本文設(shè)計(jì)了7組方鋼管UHPC組合墩柱模型，主要考慮了軸壓比、長(zhǎng)細(xì)比、套箍系數(shù)3個(gè)影響參數(shù)。模型編號(hào)SC-T8-30-A、SC-T8-40-C、SC-T6-40-A等為設(shè)置的不同軸壓比、長(zhǎng)細(xì)比、套箍系數(shù)的對(duì)照組，具體設(shè)計(jì)參數(shù)見表1。

表1 方鋼管UHPC組合墩柱模型參數(shù)

2 有限元模型

運(yùn)用大型有限元軟件ABAQUS建立方鋼管UHPC組合墩柱的整體計(jì)算模型。組合墩柱整體模型見圖2，其中UHPC柱、鋼管均采用三維八節(jié)點(diǎn)六面體減縮積分單元C3D8R劃分，采用此單元?jiǎng)澐挚稍跐M足計(jì)算精度要求的前提下，節(jié)省計(jì)算時(shí)間；內(nèi)置鋼筋采用線性桁架單元T3D2進(jìn)行網(wǎng)格劃分。

圖2 組合墩柱整體模型

2.1 材料本構(gòu)模型

2.1.1UHPC受壓本構(gòu)模型

UHPC受壓本構(gòu)模型采用文獻(xiàn)[8]中提出的單軸受壓本構(gòu)模型(見式(1))，采用能量法(見式(2))計(jì)算混凝土受壓損傷。

(1)

(2)

式中：fc為UHPC抗壓強(qiáng)度設(shè)計(jì)值；n為UHPC彈性模量與割線模量比值，n=E0/Esec；ξ為UHPC應(yīng)變率，ξ=ε/ε0；ε0為UHPC峰值應(yīng)變；ε為應(yīng)變；σ為應(yīng)力。本文UHPC軸向抗壓強(qiáng)度為100 MPa，峰值應(yīng)變?yōu)?.003，彈性模量為50.1 GPa。

2.1.2UHPC受拉本構(gòu)模型

UHPC受拉本構(gòu)模型采用文獻(xiàn)[9]中提出的雙線性受拉本構(gòu)關(guān)系，應(yīng)力-應(yīng)變關(guān)系見式(3)，采用能量法見式(2)計(jì)算混凝土受拉損傷。

(3)

式中：fct為UHPC應(yīng)變硬化階段平均應(yīng)力；εca為UHPC峰值應(yīng)變；εpc為UHPC極限應(yīng)變。本文UHPC軸向抗拉強(qiáng)度為5.6 MPa，峰值應(yīng)變?yōu)?98×10-6，彈性模量為50.1 GPa。

2.1.3鋼管本構(gòu)模型

鋼管選用理想彈塑性本構(gòu)模型，在小范圍內(nèi)變形時(shí)各向同性，服從Mises屈服準(zhǔn)則，其應(yīng)力-應(yīng)變采用雙折線模型，忽略了鋼管強(qiáng)化階段的應(yīng)力增加，僅考慮彈性和屈服階段，具體取值見圖3。

圖3 鋼管應(yīng)力-應(yīng)變曲線

2.2 接觸與邊界條件

UHPC與方鋼管接觸面的相互作用包含兩部分：切向作用和法向作用。其中切向作用定義為有摩擦，用“罰”函數(shù)，摩擦系數(shù)取0.3；法向作用采用“硬”接觸以保證力的傳播。接觸面設(shè)置剛度較大的鋼管為主接觸面，UHPC面為從屬接觸面。方鋼管UHPC組合墩柱底部采用完全固定(U1=U2=U3=UR1=UR2=UR3=0)限制其自由度，模擬UHPC組合墩柱真實(shí)的工作狀態(tài)。

2.3 加載方式

采用力加載控制與位移加載控制2種加載方式。考慮到后處理的便捷性，采用選取參考點(diǎn)的方式進(jìn)行加載，參考點(diǎn)A位置見圖2。首先在UHPC組合墩柱頂部中心建立參考點(diǎn)A，然后將參考點(diǎn)A與加載面建立耦合約束，最后將豎向軸力荷載和水平位移荷載施加在參考點(diǎn)A上。

水平位移往復(fù)荷載采用Amplitudes創(chuàng)建表格來(lái)模擬地震作用，規(guī)定受壓為正方向。水平位移荷載加載規(guī)律見圖4。

圖4 水平位移加載規(guī)律

3 結(jié)果分析

3.1 滯回曲線

不同影響參數(shù)下方鋼管UHPC組合墩柱的滯回曲線見圖5。

圖5 滯回曲線

由圖5可見，7組UHPC組合墩柱的滯回曲線都有一些共同特征，滯回曲線基本呈“梭”形，表明該組合墩柱有良好的耗能能力和較好的塑性。加載初期，曲線的斜率基本呈線性發(fā)展，加載剛度與卸載剛度一致，UHPC組合墩柱幾乎未發(fā)生變形，1次完整循環(huán)所圍成的封閉滯回環(huán)面積很小，在此階段幾乎沒有產(chǎn)生能量耗散。鋼管屈服后，隨著水平位移的不斷加大，剛度逐漸減小，滯回環(huán)比加載初期飽滿。水平荷載達(dá)到峰值后，加載與卸載剛度進(jìn)一步降低，滯回環(huán)面積增大，滯回形狀更加飽滿。

從圖5a)可以看出，軸壓比在0.3～0.5的范圍內(nèi)，當(dāng)加載水平位移相同時(shí)，軸壓比越大，滯回環(huán)所圍成的面積越小。從圖5b)可以看出，長(zhǎng)細(xì)比在20～29的范圍內(nèi)，當(dāng)加載水平位移相同時(shí)，長(zhǎng)細(xì)比越大，滯回環(huán)所圍成的面積越小。從圖5c)可以看出，套箍系數(shù)在0.32～0.54的范圍內(nèi)，當(dāng)加載水平位移相同時(shí)，套箍系數(shù)越大，滯回環(huán)所圍成的面積越大。

3.2 骨架曲線

不同影響參數(shù)下方鋼管UHPC組合墩柱的荷載-位移骨架曲線見圖6。

圖6 骨架曲線

由圖6可見，UHPC組合墩柱骨架曲線均關(guān)于原點(diǎn)對(duì)稱，表明UHPC組合墩柱正反向受力性能穩(wěn)定。彈性階段，除了長(zhǎng)細(xì)比不同的UHPC組合墩柱剛度出現(xiàn)明顯差異外，其余UHPC組合墩柱剛度基本一致。彈塑性階段，鋼管屈服，骨架曲線開始出現(xiàn)差異。

從圖6a)可以看出，軸壓比在0.3～0.5的范圍內(nèi)，峰值承載力隨軸壓比的增大而減小。軸壓比對(duì)骨架曲線的上升段曲線形狀影響較小，到達(dá)峰值荷載后水平承載力隨著軸壓比增加下降趨勢(shì)加快。與SC-T8-30-A相比，SC-T8-50-A的峰值承載力下降了14%。從圖6b)可以看出，長(zhǎng)細(xì)比在20～29的范圍內(nèi)，彈性階段受力性能就有較大差異，隨著長(zhǎng)細(xì)比的增加，骨架曲線呈現(xiàn)“躺倒”的趨勢(shì)，峰值承載力也相應(yīng)的降低。與SC-T8-40-B相比，SC-T8-40-C的峰值承載力下降了37%。從圖6c)可以看出，套箍系數(shù)在0.32～0.54的范圍內(nèi)，峰值承載力隨著套箍系數(shù)的增加而增加，到達(dá)峰值荷載后，水平承載力的下降趨勢(shì)幾乎一致。與SC-T6-40-A相比，SC-T10-40-A的峰值承載力增加了34%。

3.3 延性系數(shù)

延性是衡量組合墩柱抗震性能的重要指標(biāo)之一，用延性系數(shù)μ表示，計(jì)算方法[10-11]見式(4)。

(4)

7組UHPC組合墩柱屈服、極限狀態(tài)下的荷載、位移和延性系數(shù)的計(jì)算結(jié)果見表2。

表2 有限元分析及計(jì)算結(jié)果

由表2可知，隨著軸壓比的增加，位移延性系數(shù)減小。當(dāng)軸壓比從0.3增加到0.5時(shí)，位移延性系數(shù)下降了36.9%。隨著長(zhǎng)細(xì)比的增加，位移延性系數(shù)減小。當(dāng)長(zhǎng)細(xì)比從20增加到29時(shí)，位移延性系數(shù)下降了20.3%。隨著套箍系數(shù)的增加，位移延性系數(shù)增大。當(dāng)套箍系數(shù)從0.32增加到 0.54時(shí)，位移延性系數(shù)上升了19.4%。因此降低軸壓比、增大套箍系數(shù)，控制長(zhǎng)細(xì)比可提高組合墩柱的延性。

本文中方鋼管UHPC組合墩柱的延性系數(shù)為2.92～4.63。除試件SC-T8-50-A延性系數(shù)為2.92，其余組合墩柱的延性系數(shù)均大于3，表明方鋼管UHPC組合墩柱具有良好的塑性變形能力和抗倒塌能力。

3.4 耗能能力

耗能能力是反映結(jié)構(gòu)抗震性能是否良好的重要指標(biāo)之一，具體表現(xiàn)為在反復(fù)荷載的作用下，方鋼管UHPC組合墩柱滯回曲線循環(huán)一周后所圍成的封閉滯回環(huán)面積的大小，數(shù)值越大，說(shuō)明UHPC組合墩柱的抗震性能越好，抵抗地震作用的能力越強(qiáng)。組合墩柱累積滯回耗能可以根據(jù)每一次反復(fù)荷載下的滯回耗能累加計(jì)算得到。

不同影響參數(shù)下UHPC組合墩柱的累積滯回耗能曲線見圖7，其中橫坐標(biāo)為位移，縱坐標(biāo)為累積滯回耗能。從圖7a)可以看出,組合墩柱軸壓比越大，其累積滯回耗能越低。當(dāng)水平位移加載到60 mm時(shí)，SC-T8-30-A的累積耗能是SC-T8-50-A的1.43倍。從圖7b)可以看出，長(zhǎng)細(xì)比越大，試件累積滯回耗能越低。當(dāng)水平位移加載到60 mm時(shí)，SC-T8-40-B的累積耗能是SC-T8-40-C的2.87倍。從圖7c)可以看出，套箍系數(shù)越大，試件累積滯回耗能越高。當(dāng)水平位移加載到60 mm時(shí)，SC-T10-40-A的累積耗能是SC-T6-40-A的1.38倍。

圖7 累積耗能-位移曲線

4 結(jié)論

1) 方鋼管UHPC組合墩柱的滯回曲線均較為飽滿，呈現(xiàn)“梭”形，具有良好的滯回性能。

2) 軸壓比在0.3～0.5的范圍內(nèi)，組合墩柱的承載力、延性、累積耗能隨軸壓比增加而降低；長(zhǎng)細(xì)比在20～29的范圍內(nèi)，組合墩柱的承載力、累積耗能隨長(zhǎng)細(xì)比增加而降低，延性隨長(zhǎng)細(xì)比增加呈現(xiàn)先減小后增大的趨勢(shì)；套箍系數(shù)在0.32～0.54的范圍內(nèi)，組合墩柱的承載力、延性、累積耗能隨套箍系數(shù)增加而增加。

3) 方鋼管UHPC組合墩柱的延性系數(shù)在2.92～4.63之間，累積滯回耗能在0.48×105～1.4×105J之間，需將軸壓比、長(zhǎng)細(xì)比與套箍系數(shù)控制在合理范圍內(nèi)，才能達(dá)到最佳性能。