在小學低年級計算教學中如何培養學生的知識遷移能力

魏彤

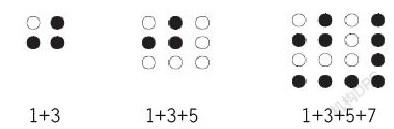
【摘 要】小學低年級階段的學習是整個學習體系的基礎，而計算教學在小學數學教學中至關重要。計算教學的主要作用在于培養學生的計算思維和運算能力，因此，在計算教學過程中，教師不僅要注重學生對計算方法的掌握，還要注重學生將數學知識應用于實際問題的能力的培養，即培養學生的知識遷移能力。遷移作為培養學生的數學能力以及問題解決能力的有效突破口，教師應該尤為注意遷移教學的高效性，要培養學生舉一反三的能力，提升自身的數學素養。本文從低年級實際情況出發，淺析在小學低年級計算教學中該如何培養學生的知識遷移能力。

【關鍵詞】小學低年級;計算;知識遷移

學校教育對于人的發展尤為重要，而學校教育的核心就是要讓學生能夠以舊帶新，掌握好的學習方法，做到知識的遷移，而并非灌輸課本知識。而對于低年級的小學生而言，他們的數學知識儲備比較少，數學思維能力有待完善和提升，但是求知欲和好奇心都比較旺盛。所以，在這個階段，教師要能夠提供足夠的指導，幫助學生由抽象聯系實際，從而逐漸培養知識遷移能力。那么，在小學低年級的計算教學中，作為教師該如何更好培養學生的知識遷移能力呢？

一、加強學科知識的理解，夯實遷移基礎

全面深刻地理解、概括數學課程的一般原則是實現知識遷移的一條非常重要的途徑。因此，在數學課堂教學時，要積極引導學生運用原有的知識經驗去理解新學習的內容。在這一學習過程中，教師應該提前了解學生情況，判斷學生是否滿足要求，倘若不能，也就是當學生出現已有的儲備知識對于新知識的理解有困難的情況時，教師就要及時的給學生補充必要的知識，為以后學習打下基礎，也為知識遷移打好基礎。

例如在教學一年級的加減法之前，學生必須對于前面的《分與合》的內容有了較為深刻的記憶和理解，才能以這些知識為基礎，遷移到10以內的加減法的學習，如果學生對于《分與合》的內容不理解也沒有記憶，那么他們將會對這一部分乃至后面20以內的加減法以及100以內的加減法的計算學習感到非常吃力。

二、創設新舊知識聯系的情景，搭建遷移橋梁

知識遷移的根本是原有知識。因此，原有的知識是堅實的基礎。因此，有效的知識遷移需要新舊知識的聯系，這就要求在課堂教學中，教師不僅要重視向學生傳授知識，還要能夠引導學生聯系已經掌握的知識。因此，教師可以設置情景來聯系新舊知識，從而搭建遷移橋梁，實現知識的遷移。

例如在教學一年級20以內的加減法中的《8、7加幾》這一課的內容時，由于在前一課時學生已經有了計算9加幾的計算經驗了，而這兩節課中涉及到的計算方法和計算原理是相似的，因此教師可以在教學時先出示幾道9加幾的算式讓學生計算并且讓學生說說計算的過程，同時在探究8加幾計算方法的過程中引導學生用學過的方法試著算一算，從而實現知識遷移。

三、強化直觀抽象教學間的聯系，促進知識的遷移

數學學科具有抽象性，從而良好的抽象概括能力，對于學生學好數學學科尤為重要，同時也有助于提高學生知識遷移能力。如果學生概括事物的能力很強，那他們對于知識的遷移能更有效地切入，從而更好地掌握新知識。因為進行抽象概括的基礎是具有較強的感性認識，所以教師在引導學生進行抽象概括時，應該鼓勵學生對于具體形象的事物盡可能多的積累，從而提升感性方面的認識。在教學時，教師應充分利用具體的教具，學生充分利用具體的學具，使得學生感受直觀與抽象間的聯系。

我們知道，計算教學中最常用的教具就是小棒和計數器了，而低年級的孩子對于抽象的數學知識理解起來更是有困難，因此在實際教學時，要讓學生能自己動手來實踐體會。例如在教學二年級認識萬以內的數這一部分內容時，其中關于數的組成這一課時，是完全建立在認識小棒和計數器的基礎之上的。只有當學生掌握了一小捆小棒是“十”，一大捆小棒是“一百”，以及關于計數器中的相關知識之后，才能進行這一部分的學習。還有在教學一年級的分與合，在課上，也是要依靠小棒去進行探究各個數的分成與合成，倘若完全靠學生在頭腦中想象每個數的分與合，教學效果肯定大打折扣，畢竟低年級的孩子比較小，他們是理解不了的。

四、注意科學合理的練習，在舉一反三中促進遷移

能夠突破教學中的重難點是教師在所有教學活動中的主要任務和障礙。正所謂要究其根本、對癥下藥。因此要突破課上的重難點，首先一定要明確教學中的“重”和“難”分別在哪里，接著要運用合理、正確的教學策略，最后要落實精講精練的原則，讓學生能自主聯系新舊知識。在課上，教師應注重設計科學合理的練習，只有設計出具有針對性、階梯性和啟發性的練習，才能讓學生充分利用遷移規律去解決實際問題，同時也為后繼學習的進一步遷移做準備。

例如：規律計算題（如下圖）根據圖中的規律以及下面的算式，完成第四幅圖且寫出對應的算式。

根據圖可以看出圖形的規律：在前一幅圖的基礎上又增加了一圈小圓圈，每次增加的個數都是比前一圈的小圓圈個數多兩個，而小圓圈有實心的有空心的，第一圈空心，第二圈實心，第三圈空心……以此類推，而算式就是根據對應圖形的規律算出一共有多少個小圓圈。從這一題中可以看到，在數學教學中，很多的知識都是相通的，數字計算可以用生動的圖形來表現，而圖形也可以用準確的數字來體現。學生在這一題中體會到了數字和圖形之間的聯系，當遇到類似的問題也會想到這種方法。

五、調整知識間的同化，避免形成負遷移

在教學中，當舊的學習經驗影響到新學的知識時，稱為負遷移。正遷移一般是建立在深入研究的基礎上，而負遷移一般是對于知識的理解停留在表面，沒有真正的理解。產生負遷移的前提一般是概念之間的共同因素，由于學生處在低年級階段，他們往往對于相關概念的本質區別不易察覺，因此教師應該在教學中對于容易混淆的概念進行辨析對比，講清內涵，揭示特征，避免負遷移的產生。

例如教學文字計算題：2個4相加的和是多少？以及2個4相乘的積是多少？學生在解決這兩個問題時特別容易出錯。這兩個題目乍一看差不多，都是2個4，但是它們的本質是不同的。2個4相加可以列成算式4加4，也可以根據乘法含義列成算式2乘4，但是2個4相乘則只能列成算式4乘4。大多數學生對于這兩道題出錯的原因在于看到了“2個4”，第一反應就是根據“求幾個幾是多少用乘法計算”列出算式2乘4，并沒有深入思考，就產生了負遷移。對于這兩個題目，教師一定要讓學生理解清楚題目的意思，明確題意之后再進行解答。

總之，提高學生的數學思維能力是數學教學的重中之重，而遷移能力又是數學思維的重要部分，因此在今后的數學教學中，廣大數學教師還應繼續努力，為創造出培養學生知識遷移能力的更多、更好的策略而做出自己應有的貢獻。

【參考文獻】

[1]王宗梅.遷移規律，讓兒童的數學思維能力逐步提升[J].黑河教育，2018.

[2]孫孝忠.對當前小學數學課堂教學中一些現象的理性思考[J].江蘇教育（小學版），2009.12

[3]王志民.連接生活素材感悟數學魅力[J].教學與管理（小學版），2009.1