魯棒邊緣粒子濾波及在目標跟蹤中應用

王宗原，周衛東

(1.哈爾濱工程大學 數學科學學院，哈爾濱 150001; 2.哈爾濱工程大學 智能科學與工程學院，哈爾濱 150001)

0 引言

濾波是基于從初始時間到當前時間的噪聲測量對當前狀態進行估計的一種方法。已經被廣泛應用于許多領域，如目標跟蹤、導航、機器人控制和信號處理[1-4]等。粒子濾波是利用加權粒子求和方法進行非線性狀態空間模型狀態估計的高效方法。但是高維狀態如果直接用粒子濾波求解會產生維數災難，導致粒子濾波崩潰而無法應用[3]。為了提高粒子濾波廣泛的實際應用性，目前普遍關注的是從系統模型結構出發探究其是否具有條件線性子結構，從而通過狀態降維方法進行狀態估計。通過查閱已有文獻可知，這一類模型在導航和目標跟蹤領域廣泛存在。目前估計最有效方法是利用Rao-Blackwellised思想設計的粒子濾波(RBPF)，或稱為邊緣粒子濾波[5]，它將粒子濾波與線性最優的卡爾曼濾波巧妙融合完成整體狀態估計。

邊緣粒子濾波由于其更優異的濾波設計方案，一經出現在導航和目標跟蹤及動態貝葉斯網絡中就取得成功應用，而且為適應不同系統模型及量測出現的各種新問題，近幾年來研究人員對RBPF及其不同改進形式進行了廣泛研究，例如，文獻[6]中提出用遞推期望最大化方法開發具有跳躍馬爾科夫鏈和系統結構分解的Rao-Blackwellised粒子濾波算法；同時文獻[7]利用Rao-Blackwellised準則結合RBPF平滑解決混合線性狀態空間模型具有量測失序的RBPF算法性能下降問題，通過標準常加速模型的仿真結果，表明所提算法精度具有超過RBPF精度10%的性能；再有文獻[8]考慮了混合線性模型線性狀態方程噪聲之間及狀態方程噪聲與量測噪聲相依賴的情況，利用格萊姆-施密特解耦方法實現全部噪聲協方差矩陣的對角化形式，并在常速目標跟蹤模型仿真中取得優于標準RBPF精度的結果；進一步文獻[9]將RBPF框架擴展到系統全部為非線性方程的模型中得到分散粒子濾波(DPF)，不同于卡爾曼濾波粒子濾波混合求解過程，DPF通過兩次權值及兩次重采樣計算得到兩次粒子混合估計結果。由以上的文獻描述可見RBPF算法適用各種新出現系統問題的改進形式已被廣泛探究，并且得到優于標準RBPF的結果。但據作者所知，RBPF量測噪聲參數未知的改進形式還沒有被涉及。

雖然模型參數未知的貝葉斯濾波已通過狀態擴維法[10]或交互式多模型(IMM)法[11]進行了研究，但它們對噪聲參數未知情形還無法解決。近期文獻[12-13]針對噪聲異常情況通過變分推斷理論給出魯棒高斯近似濾波算法，并在目標跟蹤模擬中得到成功應用，但標準無跡卡爾曼濾波(UKF)或擴展卡爾曼濾波(EKF)由于樣本點有限或線性化誤差原因對于相同導航或目標跟蹤問題精度低于邊緣粒子濾波或其變形的DPF[14-15]。另外，水下運載器地形輔助導航[16]、重力梯度輔助導航等組合導航估計方法也均采用RBPF[17]，這是因為這些基于數據庫圖的地球物理場導航只能通過粒子表示載體全部可能位置，而且隨著粒子數增加，導航精度還可能繼續提高。

RBPF的另一個重要應用是在目標運動分析(TMA) 領域，也即目標跟蹤，這屬于通過方位測量對運動目標狀態進行估計的范疇[18]。由單運動觀測器收集量測形式已在無源傳感領域(如聲納或雷達)具有廣泛應用[19]，過去幾年成為研究熱點。現在關注的是用遞推貝葉斯方法得到狀態后驗概率密度函數(PDF)。TMA的特點通過觀測平臺的運動對目標距離進行觀測。下面將討論貝葉斯TMA的平面跟蹤問題，它將從一維方位量測集獲得四維狀態后驗PDFs，狀態包含目標位置和速度。但高機動目標跟蹤通常會產生量測噪聲異常問題[12-13]，影響量測噪聲因素有接觸實際角度、目標的距離和相對速度、信噪比、接收陣列形狀、傳播信道等等，這些因素很少能準確知道并且隨時間推移而變化，因此工程實際中精確知道量測方差幾乎是不可能的，這就造成 TMA量測噪聲方差時變未知且包含異常值的特性。

注意到現有邊緣粒子濾波及其各種改進形式都沒對量測噪聲時變的目標跟蹤問題給出有效解決方案，這或許是由于如何在RBPF引入噪聲參數實時估計的方法還沒有被探究。為了設計具有量測方差自適應估計能力的混合系統模型的魯棒邊緣粒子濾波算法，本文將探究使用Rao-Blackwellised原理及變分推斷公式對混合系統量測噪聲異常問題進行狀態估計，并在典型TMA的平面跟蹤模型中進行仿真驗證。

1 混合模型及邊緣粒子濾波

1.1 目標跟蹤模型

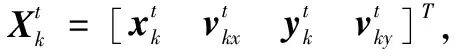
Xk+1=FkXk-Uk+1,k+Gkwk

(1)

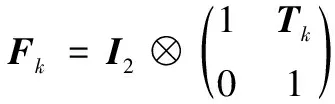
純角度觀測模型為:

zk=atan2(xk,yk)+vk

(2)

atan2(·)表示四象限反正切函數，此處得到k時刻目標真實角度。觀測噪聲vk～N(0,Rk)，Rk可能是時變且未知的。

1.2 混合模型及濾波

對式(1)、(2)組成目標跟蹤系統模型進行一般化引申，得到與組合導航及定位相同的如下線性非線性狀態混合模型表達式：

(3)

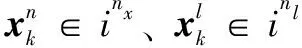
先忽略量測噪聲變化的情況，RBPF的狀態估計推導如下，聯合狀態的后驗可分解為：

(4)

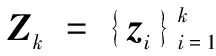
依據chapman-Kolmogorov公式，并根據高斯分布引理[12]：

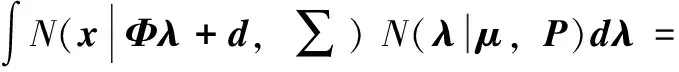
N(x|Φμ+d,ΦPΦT+∑)

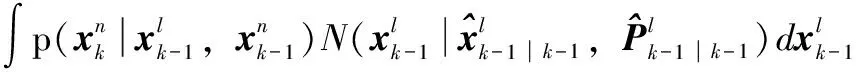
(5)

可見前一時刻線性狀態后驗對非線性狀態預測是附加噪聲，由于高斯過程噪聲，非線性狀態預測是如下高斯分布形式：

(6)

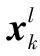
(7)

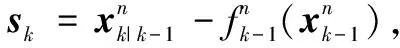
(8)

其中參數為:

(9)

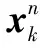
(10)

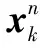
(11)

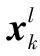
(12)

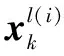
2 量測噪聲魯棒RBPF推導

下面考慮量測噪聲方差未知的情形。采用將量測噪聲方差視為先驗分布已知隨機變量，并把它應用到遞推模型中，假定狀態與量測噪聲方差相互獨立有：

p(xk,Rk|xk-1,Rk-1)=p(xk|xk-1)p(Rk|Rk-1)

(13)

其中:p(xk|xk-1)狀態遞推式，p(Rk|Rk-1)方差遞推式。利用貝葉斯濾波公式和Rao-Blackwellised法則，可用兩種方式同時求解狀態和方差后驗，第一種是如下分解:

(14)

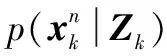
(15)

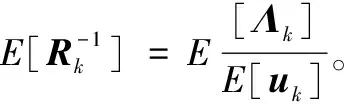
變分推斷得到的后驗近似分布公式:

q(Θi)∝exp{Eq(Θj≠i)[lnp(Θ|Z)]}

(16)

其中:Eq(Θj≠i)[lnp(Θ|Z)]表示條件聯合PDF對異于Θi的其它參數求期望[2]。下面給出適用于所提混合模型的具體推導過程，利用貝葉斯公式，非線性狀態及量測噪聲參數條件聯合分布表示為：

(17)

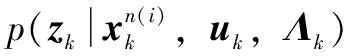
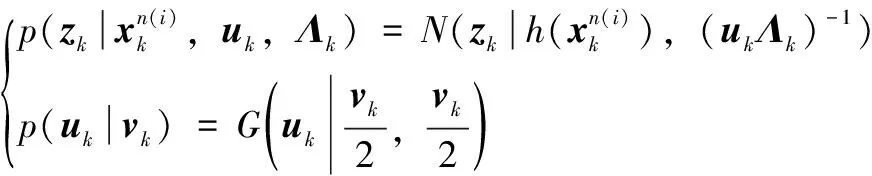
(18)

G(·|α,β)表示超參數為α,β的伽馬分布，伽馬分布與高斯分布一樣都屬于具有封閉性質共軛指數族。式(17)右端第一個表達式為高斯分布。第二個表達式噪聲參數即尺度矩陣、隱變量及自由度的聯合分布p(Λk,uk,vk)，設為伽馬分布連乘積，又根據概率乘法公式及式(18)的第二個式子，有如下表達形式：

其中：上角標jj表示對角尺度矩陣第jj個分量,jj∈{1,2,…,m}。注意此時狀態粒子權值計算式:

(19)

注意權值計算時右面量測似然是用估計的尺度矩陣與自由度的t分布表示。由于參數粒子依賴狀態粒子，因此這也是參數粒子權值表達式。

為了表示噪聲參數的變化情況，噪聲參數預測引入波動參數ρ∈(0,1)，噪聲超參數預測[2.20]表達式為:

(20)

變分推斷得尺度矩陣、隱變量及自由度參數變分后驗如下。

在(16)中令Θi=Λk，計算尺度矩陣變分后驗PDF對數為：

(21)

可見尺度矩陣更新的超參數中包含隱變量的期望E[uk]。

在(16)中,令Θi=uk，計算隱變量uk變分后驗PDFq(uk)的對數為：

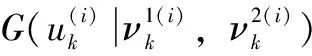
(22)

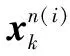
自由度變分后驗計算與線性模型自由度變分后驗計算相同，具體過程及結果參見文獻[2]。上式超參數遞推可見超參數更新過程會出現參數耦合情況，通過使用設置初始超參數值的固定點迭代方法[2]可以解決這個問題。通過概率分布的期望公式，量測噪聲分布的參數期望計算為：

(23)

所提算法一步運行過程總結如下：

魯棒邊緣粒子濾波算法:

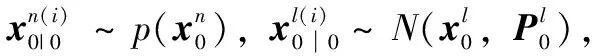
2)對每一個αk|k-1：

(1)從式(6)的建議分布提取非線性狀態預測αk|k-1，用(20)預測超參數αk|k-1，βk|k-1，

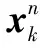
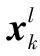
(24)

如果迭代沒終止，令k=k+1, 從步驟1開始重復上述過程。

3 仿真分析比較

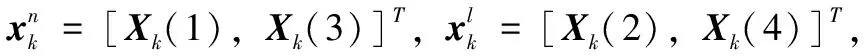
(25)

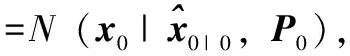
1)Rk=Rk-1+εk，εk表示量測噪聲方差遞推式的過程噪聲被建模為高斯噪聲，即：

εk～N(0,ζ2)

(26)

ζ2=0.012，單位deg2。

2) 異常時變:

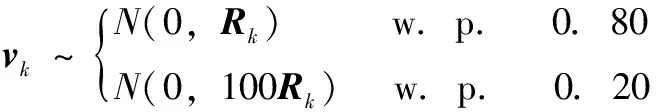
(27)

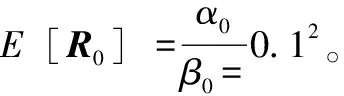
實驗通過一次獨立實驗真實位置和估計位置比較，及20次蒙特卡洛仿真均方根誤差來衡量不同算法的性能。均方根誤差(RMSE) 定義式為：

(28)

對于所給量測噪聲方差設置，此時標準RBPF算法運行經常有失效情況發生，具體為RBPF算法在迭代幾個時間步后算法失效，原因是粒子濾波運行崩潰，從而導致整個濾波失效。而所提量測魯棒邊緣粒子濾波算法則始終在每次蒙特卡洛仿真時正常穩健運行。

下面將RBPF能正常運行情況下x-y面軌跡圖及東向與北向RMSE圖進行比較。圖1～2為第一種噪聲情況下與標準RBPF算法比較的RMSE圖及軌跡圖。

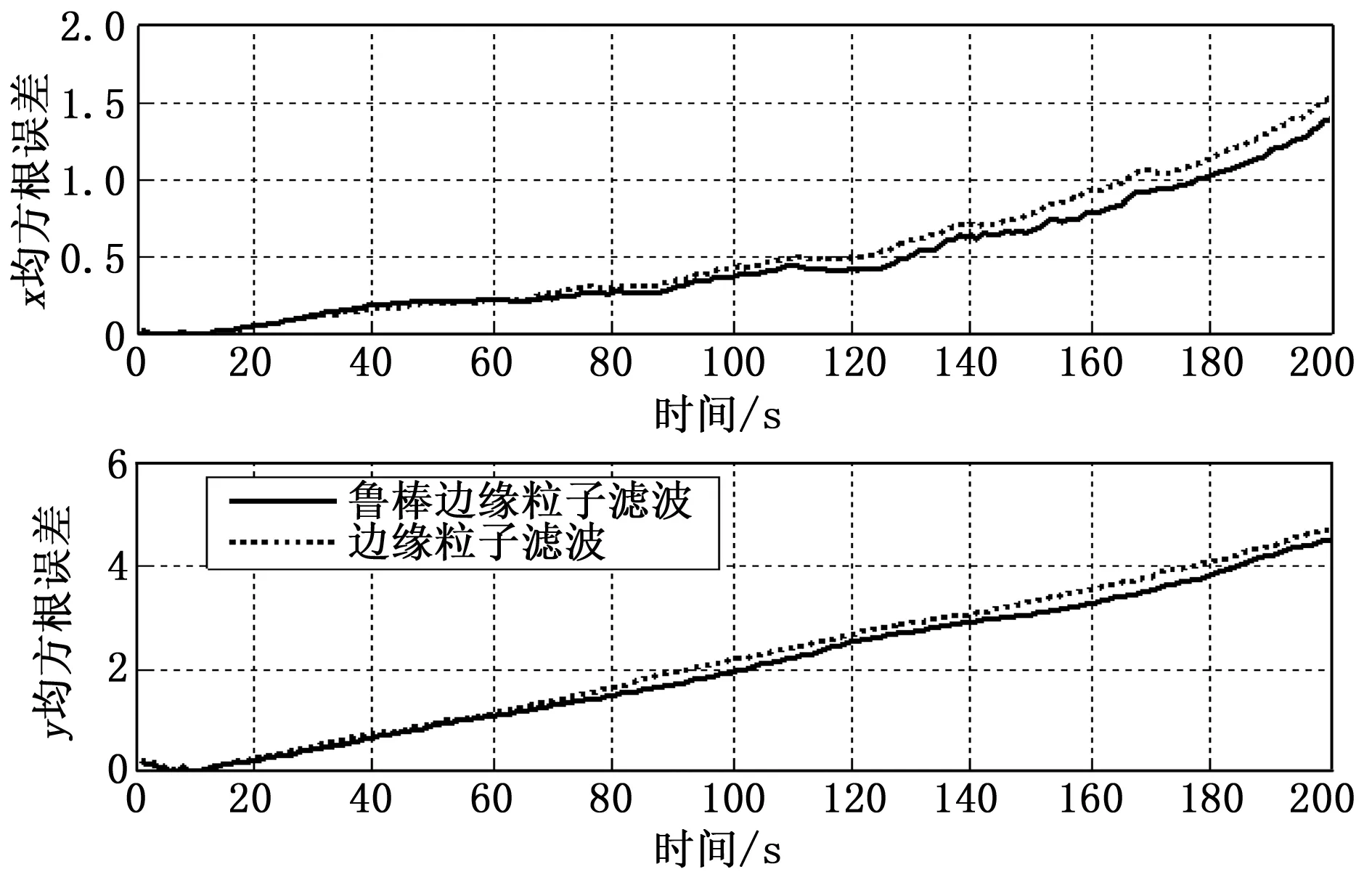
圖1 噪聲1下所提算法和RBPF算法估計軌跡RMSE比較圖

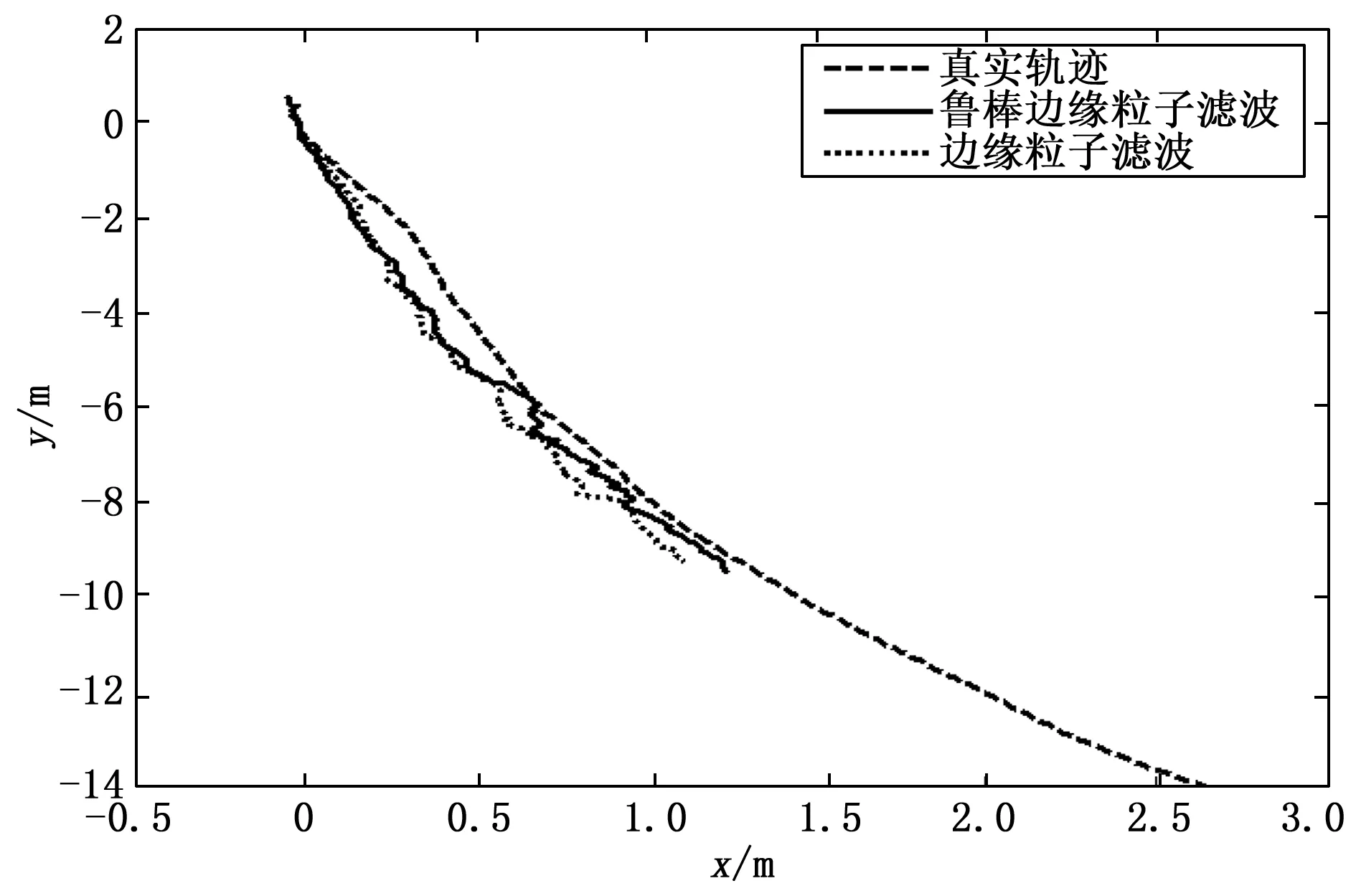
圖2 噪聲1下真實軌跡與RBPF算法和所提算法軌跡比較

表1 噪聲1下所提算法和RBPF算法目標跟蹤性能比較

從位置的具體數值上可以看到兩種算法對問題描述的目標跟蹤問題都有較高的估計精度，即使所選擇的粒子數僅為100。而所提算法在X、Y方向的RMSE精度上要略高于所比較的RBPF，說明在此種量測噪聲方差緩慢變化的情況下，所提具有方差自適應魯棒邊緣濾波算法更具有狀態估計優勢。

圖3～4為第二種噪聲情況下兩種算法的東向與北向RMSE及軌跡比較圖。從圖3～4可見，在x軸方向所提算法狀態估計精度略高于RBPF算法的精度；對于y軸方向精度可見除個別時間點外，所提算法的狀態估計精度對已有RBPF算法有較大提高；相比于RBPF位置估計，所提算法位置估計更靠近真實位置。具體數值如表2所示。

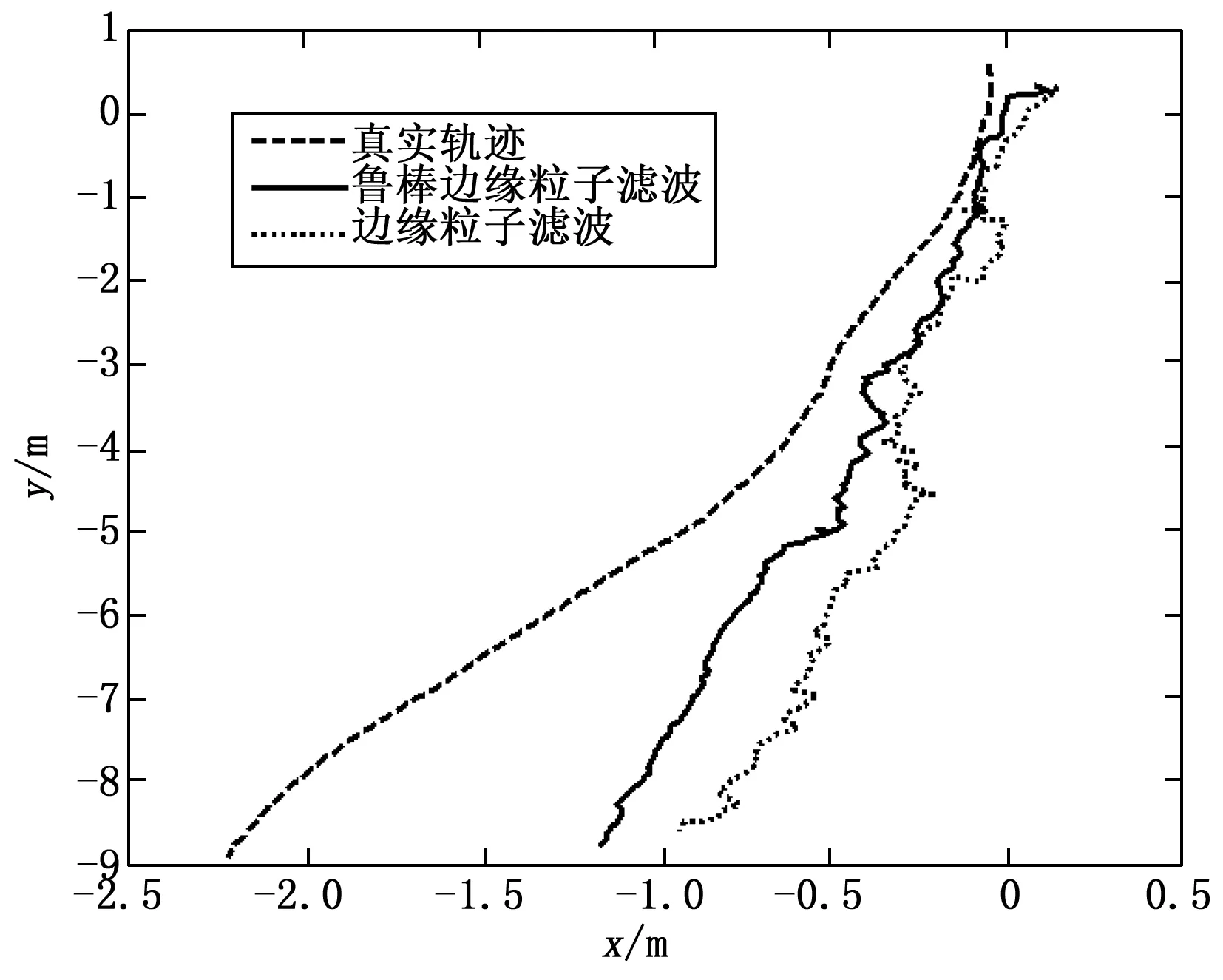
圖4 噪聲2下真實軌跡與RBPF算法和所提算法估計軌跡比較

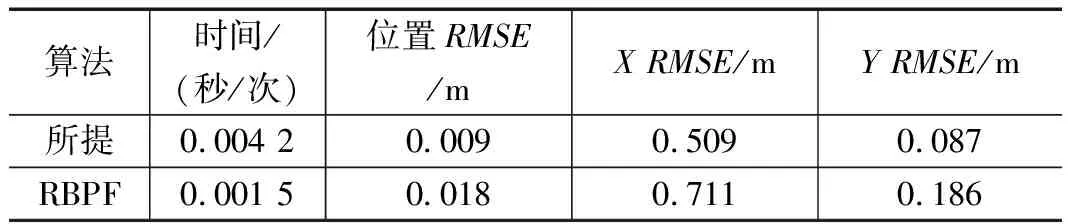
表2 噪聲2下所提算法和RBPF在目標跟蹤性能比較

第二種噪聲情況下，即使RBPF算法能夠正常運行，所提算法的精度更高，相比于第一種噪聲結果優勢更加明顯，說明第二種噪聲情況下所提算法更具有適用性。

當然，如果噪聲方差是恒定不變且事先精確已知的情況下，已有RBPF算法精度略高于所提算法，因為所提算法的方差是用算法實時估計的方差計算，而RBPF算法是用精確已知的方差，這也解釋了為什么第二種噪聲情況某小段時間內RBPF精度高于所提算法。

另外雖然所提算法在CV模型中仿真驗證，可以驗證對常加速度CA的目標跟蹤問題也同樣具有優異性能。另外所提算法單次仿真時間近似為RBPF算法單次運行時間的2.5倍。

4 結束語

由于邊緣粒子濾波在導航和目標跟蹤中的不可替代性，本文對現有邊緣粒子濾波無法解決量測噪聲方差未知的問題進行研究，通過將學生t分布加入混合模型，利用Rao-Blackwellised思想分別實現狀態條件降維及參數與狀態的同時估計，由此開發出一種魯棒邊緣粒子濾波。文中推導了噪聲參數及含有噪聲參數狀態的遞推計算公式，并把所提算法在典型目標跟蹤模型中及設置的兩種不同量測噪聲下進行仿真分析，結果表明這兩種情況下都具有更優越的估計性能。