有序貝葉斯網絡在肥胖數據中的應用
陳芳芳,徐平峰
(長春工業大學 數學與統計學院,吉林 長春 130012)
0 引 言
自1980年以來,全球肥胖人口數量劇增,且因肥胖患病和死亡人數也在攀升[1]。胖瘦程度通常用身體質量指數(BMI)來衡量。2019年BMI偏高導致全球500萬人死亡,主要死亡原因是由肥胖引起的心血管疾病和Ⅱ型糖尿病,另外,高BMI也會增加患癌癥的風險。文中目的是尋找肥胖的影響因素,以及如何在這些因素下對一個人是否肥胖進行預測。肥胖等級是有序變量,各等級之間存在自然順序,對有序變量建模不能直接使用決策樹、隨機森林等機器學習算法,這樣做會損失有序信息,正確的做法是建立合適的有序分類器。
已經有學者提出一些算法專門用來解決有序分類問題,如有序logistic回歸[2]、有序支持向量機[3]、有序神經網絡[4]等。這些有序算法的目標都是得到準確率更高的分類器,但是影響決策的主要特征是哪些,特征之間是否存在依賴關系卻沒有探討。針對肥胖問題,文中目的不僅能正確對肥胖等級進行預測,還要尋找影響肥胖的因素及各因素之間的關系。
針對已有分類器無法同時解決有序分類問題和不善于知識表達的缺點,Halbersberg D等[5]提出一種在給定初始網絡的情況下,利用有序信息測度構建貝葉斯網絡分類器的算法。有序信息測度能反映誤分類的嚴重性,所得貝葉斯網能反映變量之間的依賴關系。但是Halbersberg方法[5]直接用樸素貝葉斯網(Naive Bayesian, NB)或者空的網絡(Empty Network, EN)作為初始網絡,而不同初始網絡的選擇可能會對分類器的性能產生影響,因此,文中用Kuschner K W等[6]的方法生成“平均”網絡(Average Network, AN)作為初始網絡,然后結合Halbersberg方法得到分類器。肥胖數據結果顯示,新方法準確率顯著提高,并且優于其他有序分類算法。從得到的貝葉斯網絡發現,飲食習慣是影響肥胖的主要因素,此外,日常乘坐的交通工具類型也會對肥胖等級產生影響。
1 預備知識
1.1 貝葉斯網絡分類器
貝葉斯網絡分類器(Bayesian Network Classifier, BNC)是用來預測離散類別變量C的貝葉斯網絡。對于一個分類問題(X,C),X=(V1,V2,…,Vm)表示觀測特征,C表示類別標簽,對應的貝葉斯網絡結構用B=〈ζ,Θ〉表示,ζ是有向無環圖,每個節點代表(X,C)中的一個變量,Θ表示量化該網絡的一組參數。給定m個特征的觀測值x=(v1,v2,…,vm),其中vi為x在第i個屬性Vi上的觀測值,則BNC為x分配最可能的類別c*,c*對應C中的某一個取值,即
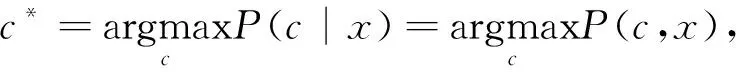
(1)
其中,P(c,x)可以根據貝葉斯網絡的結構B=〈ζ,Θ〉分解得到,即
1.2 學習貝葉斯網絡分類器
貝葉斯網絡分類器的學習包括結構學習和參數學習兩部分。結構學習通常是用搜索和評分的方法,如徐平峰等[7]提出的基于自助法(Bootstrap)的高斯貝葉斯網的結構學習算法BPKL。搜索和評分方法的基本思想是選擇一個評分函數,該評分函數能測量結構對數據的契合度,然后基于評分函數尋找結構最優的貝葉斯網。但是從所有可能的結構中尋找最優網絡是一個NP問題。能在有限時間內得到近似解有兩種方法:
1)貪心法即貪婪搜索,從某個網絡出發,通過對該網絡加邊、減邊或改變邊的方向(不形成閉環的情況下),尋找使評分函數最優的結構;
2)通過對網絡結構施加約束來縮小搜索空間。
參數學習比較容易,就是在得到網絡結構后,通過對訓練樣本計數得到每個節點的條件概率表。
1.3 評估指標
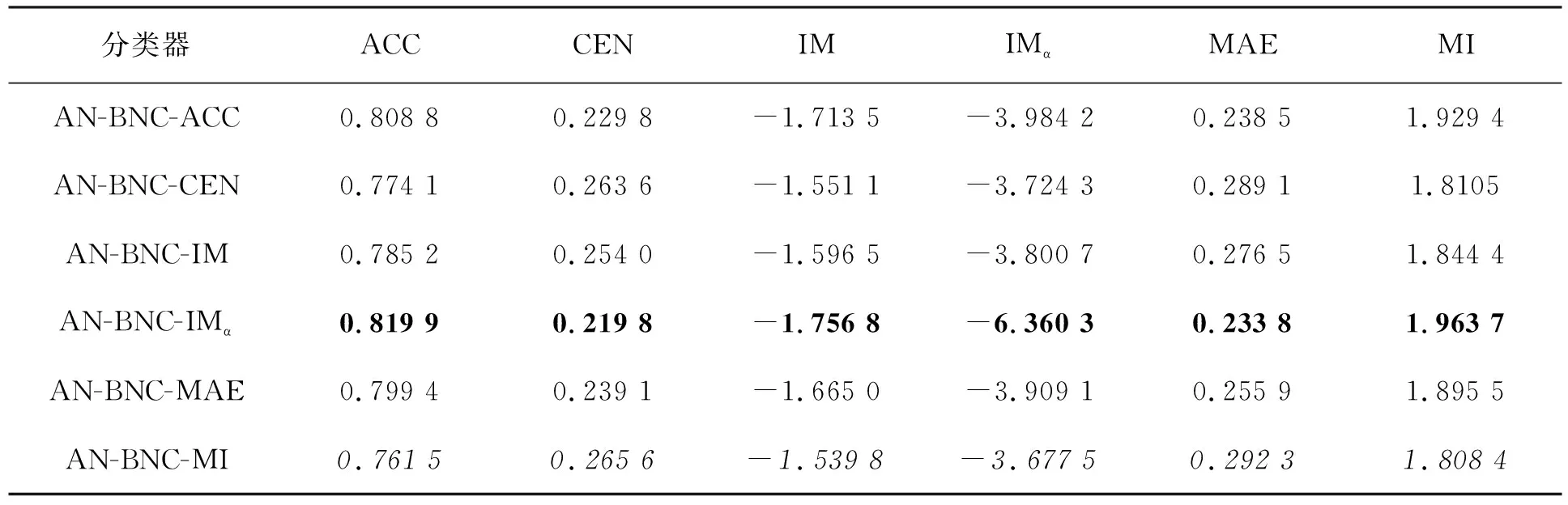
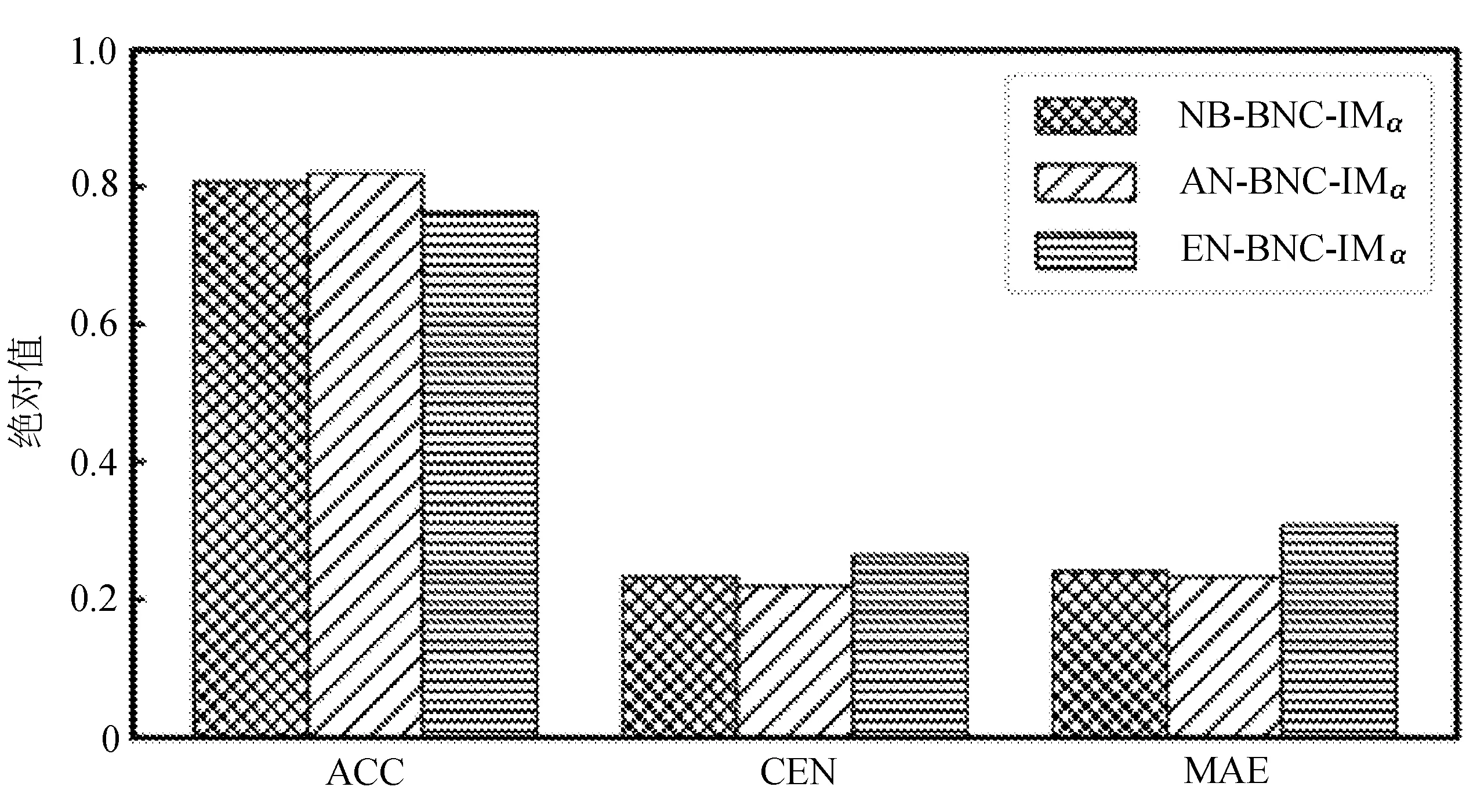
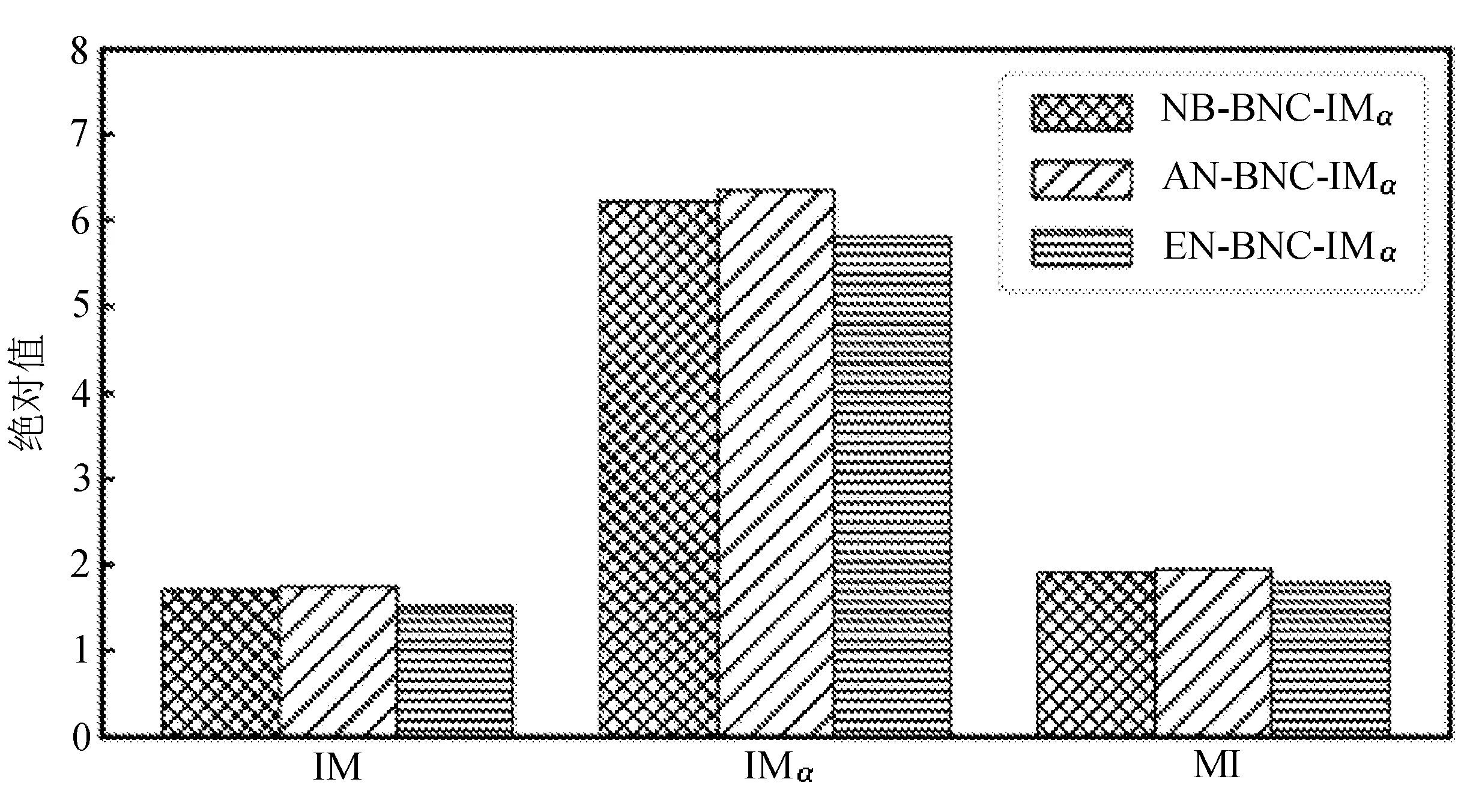
為比較不同分類器的好壞,需要進行性能評估。混淆矩陣是常用的記錄分類器性能的矩陣,包含預測值和真實值的信息。假設某個數據集的樣本量為N,可以分為k(k≥2)個類別,且類別之間是有序的,即d1 表1 混淆矩陣 令x表示預測類別,y表示真實類別。Cij(i,j∈[1,k])是混淆矩陣中位于第i行第j列的元素,表示真實類別為i而預測類別為j的樣本量,顯然 則被預測為第j類的樣本頻率為 (2) 樣本屬于第i類的頻率為 (3) 真實屬于第i類而被分到第j類的樣本頻率為 (4) 基于以上混淆矩陣可以定義一系列用來衡量分類器性能的評估指標,文中選取了6種評估指標。互信息(MI) 測量的是x和y的聯合概率分布P(x,y)和邊緣概率分布乘積P(x)P(y)的相似程度,離散變量的互信息定義為 它可以度量變量之間關系的強弱,取值越大越好。由混淆矩陣可以得到互信息的估計為 (5) 平均絕對誤差(MAE)是預測標簽x和真實標簽y之間的平均偏差,是所有可能誤差的總和,取值越小越好。由混淆矩陣可以得到 (6) 混淆熵(CEN)是Wei J M等[8]提出的一種新的評估指標。對于一個分類問題,某個標簽i錯誤分類信息既包括屬于第i類而被錯誤分到其他標簽的樣本信息,也包括其他標簽樣本被錯誤分到第i類的信息。混淆熵就是利用所有類的這種錯誤分類的分布信息來度量分類器性能,具體算法參見文獻[8]。 信息測度(IM)由Halbersberg D等[5]提出,它能同時最大化分類精度和信息,也能通過錯誤嚴重性來體現類別之間固有的順序,估計值為 IM=-MI(x,y)+ES(x,y)= (7) IMα= (8) 也可以表示為 IMα=IM-log(α)ACC, 其中,ACC為準確率,α在準確率ACC和互信息MI之間做權衡。當α=1時,IMα相當于IM,二者均越小越好。 建立分類器時需確定使用哪個度量來訓練分類器,選擇的度量方式可以和評估分類器的度量一致,如Kelner R等[9]既用準確率ACC學習分類器,也用準確率評估分類器;也可以不一致,如隨機森林可以用信息增益進行訓練,用準確率進行評估。文中應用貪心法選擇相同的衡量指標對分類器進行學習和評估,這些指標來源于文中1.3。 Halbersberg D等[5]用IMα作為評分函數搜索最優貝葉斯網絡。IMα可以用ES(x,y)來衡量有序分類中錯誤分類的嚴重性,能有效處理有序分類問題。該算法首先給出一個初始網絡和α,然后用貪心法搜索使IMα得分最低的網絡。但Halbersberg D[5]直接給定NB或者EN作為初始網絡,而不同的初始網絡得到的分類器不同,性能也不同。因此,希望通過某種方法尋找初始網絡,利用該初始網絡能提高最終分類器的性能。 Kuschner K W等[6]在建立貝葉斯網分類器時,將類別變量放在根節點處,根據互信息和條件互信息建立類別變量的馬爾可夫毯(某節點的馬爾可夫毯由該節點的父節點、子節點和子節點的其他父節點構成),同時也關注類別變量的子節點和其他變量的依賴關系。由于類別變量沒有父節點,該方法簡化了尋找貝葉斯網的過程,故用Kuschner方法[6]建立初始網絡,然后結合Halbersberg方法[5]構建最終的貝葉斯網絡形成算法1,見表2。 表2 算法1 文中將用X作為初始網絡,Y作為評分函數,得到的BNC記作X-BNC-Y,其中X∈{NB,EN,AN},Y∈{ACC,CEN,IM,IMα,MAE,MI}。 文中選取來自Kaggle網站中的obesity數據集進行分析,該數據集包括17個特征共2 111個樣本。類別變量分為體重偏輕、正常體重、Ⅰ級超重、Ⅱ級超重、Ⅰ級肥胖、Ⅱ級肥胖和Ⅲ級肥胖7個等級。除類別變量外,其余特征可分為3個方面: 1)與飲食習慣相關的特征。包括經常使用高熱量食物、蔬菜攝入頻率、正餐次數、零食頻率、每日飲水量和飲酒量。 2)與身體狀況相關的特征。包括卡路里消耗監測、體育鍛煉頻率、使用科技設備時間、使用的交通工具。 3)其他特征。包括性別、年齡、身高、體重、家庭肥胖史、是否抽煙,其中年齡、身高、體重是連續變量,將其進行離散化。 將1.3中的6種評估指標分別作為評分函數用算法1得到各自的BNC,對每個分類器在測試集上得到的混淆矩陣計算6種評估指標,所得結果見表3。 表3 相同初始網絡不同評分函數所得分類器的結果比較 用NB和EN作為初始網絡分別得到NB-BNC-IMα和EN-BNC-IMα,與AN-BNC-IMα進行比較,如圖1所示。 (a) ACC、CEN、MAE (b) MI和取絕對值之后的IM和IMα 從圖1可知,AN-BNC-IMα在6種評價指標中的表現一致優于另外兩種分類器,說明AN-BNC-IMα較Halbersberg原始方法性能好。 將AN-BNC-IMα與其他有序分類算法進行比較,選擇的比較算法有POM[2]、SVOREX[3]、NNOP[4]、ORBoost[10],這些方法都是傳統分類器用于解決有序分類問題的變體,可以用ORCA(Ordinal Regression and Classification Algorithms)[11]來實現。ORCA是一個Matlab框架,它實現并集成了不同的有序分類算法,且有專門設計的評估指標,可以衡量分類器的性能。比較的評估指標是ACC和MAE,結果如圖2所示。 圖2 AN-BNC-IMα和其它有序分類器的比較 從圖2可知,AN-BNC-IMα的準確率最高,NNOP次之,準確率相差2%;ORBoost的MAE最低,但是NNOP和AN-BNC-IMα的MAE也只有0.23,和ORBoost相差不到0.01。說明ORBoost、NNOP和AN-BNC-IMα3個分類器的性能相近,但是由于ORBoost、NNOP只給出分類結果,無法說明哪些特征對目標變量有直接影響,而貝葉斯網絡可以直觀地顯示出變量之間的依賴關系,更有利于結果的解釋,所以認為AN-BNC-IMα是最理想的分類器。 算法1得到的貝葉斯網絡如圖3所示。 圖3 貝葉斯網絡 從圖3可以看出,影響肥胖程度的主要因素除年齡、性別、身高等基本情況外,主要與飲食習慣相關的屬性,即高熱量食物、蔬菜攝入頻率、主餐次數、零食頻率有關,另外還和交通工具有關。 對交通工具這一特征進行分析發現,使用摩托車、自行車和步行的樣本占比極少,只占總樣本量的3.5%,故只分析乘坐汽車和公共交通的人群。使用公共交通和汽車的人群在各肥胖等級中的占比如圖4所示。 圖4 使用公共交通和汽車的人群在各肥胖等級中的占比 從圖4可以看出,乘坐公共交通的人群中體重偏輕、正常或屬于Ⅲ級肥胖的比例顯著大于在乘坐汽車的人群中同等級的占比;乘坐汽車的人群肥胖等級波動很大,Ⅲ級肥胖人數占比最少,Ⅱ級超重、Ⅰ級肥胖、Ⅱ級肥胖的比例較高,并且顯著大于公共交通中同等級所占的比例。這說明和乘坐汽車的人群相比,乘坐公共交通工具的人群不容易肥胖,但是Ⅲ級肥胖除外。 采用Kuschner K W等[6]的AN方法建立初始網絡,然后結合Halbersberg方法構建有序貝葉斯網絡分類器,彌補了Halbersberg方法隨機選擇初始網絡的不足。文中方法在肥胖數據上的結果顯示,和使用樸素貝葉斯網(NB)或者空的網絡(EN)作為初始網絡相比,用AN作為初始網絡所得分類器的性能在6種評估指標中一致最優,說明文中方法較Halbersberg方法效果提升明顯。另外和其他有序分類器比較發現,在準確率和平均絕對誤差上,文中方法顯著優于SVOREX、POM,并且和NNOP、ORBoost的性能相當。而且可以通過貝葉斯網直觀得出各變量之間的依賴關系,找到影響目標變量的直接因素,有助于結果解釋。從得到的貝葉斯網絡發現,影響肥胖的因素除了和飲食習慣相關的屬性外,還與日常使用的交通工具有關。
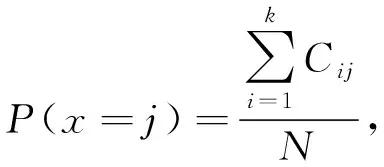
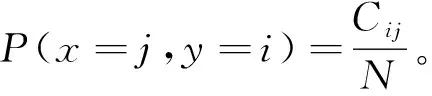
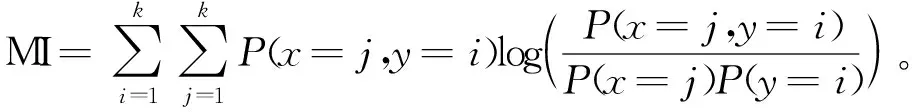
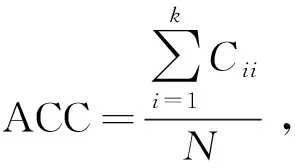

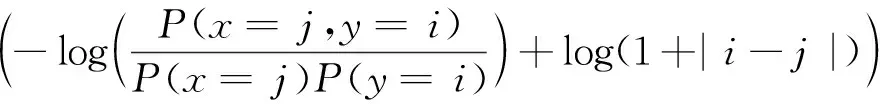
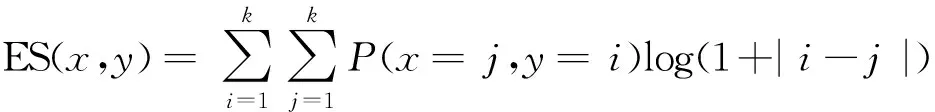
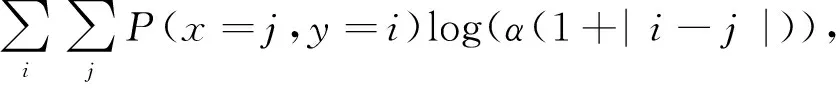
2 改進算法

3 實證分析
3.1 數據描述
3.2 算法應用及比較

3.3 影響因素分析


4 結 語

