基于非對稱GARCH-MIDAS模型的原油價(jià)格波動預(yù)測

董小剛，費(fèi)佳欣，秦喜文

(長春工業(yè)大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，吉林 長春 130012)

0 引 言

原油作為人類生產(chǎn)的必需品，學(xué)者們對其價(jià)格、波動等進(jìn)行了研究。大多數(shù)文獻(xiàn)利用原油價(jià)格的歷史信息，基于GARCH類模型預(yù)測油價(jià)的條件波動[1]。Peny Sadorsky等[2]表明GARCH類模型比任何其他競爭模型產(chǎn)生更準(zhǔn)確的預(yù)測。波動率測量和建模包含在GARCH框架中，鑒于超高頻數(shù)據(jù)的廣泛可用性，當(dāng)前大多數(shù)做法是以已實(shí)現(xiàn)波動率的眾多變體之一的形式直接測量波動率，然后建立預(yù)測模型。Nomikos Nikos K等[3]使用Mix-GARCH和MRS-GARCH模型預(yù)測1 d的原油價(jià)格波動。Sang Hoon Kang等[4]將ARFIMA模型與GARCH模型相結(jié)合，產(chǎn)生1、5、20 d的預(yù)測。但是這類預(yù)測涉及原油價(jià)格的歷史數(shù)據(jù)分析，忽略了綜合影響預(yù)測目標(biāo)的各種外部因素。

原油價(jià)格受到一系列動態(tài)和多維因素的驅(qū)動，因此，在預(yù)測原油價(jià)格波動時(shí)，考慮原油價(jià)格的影響因素，需要構(gòu)建一個(gè)合理的預(yù)測模型。為了提高預(yù)測精度，大多數(shù)研究人員在預(yù)測模型中引入了有效因素。考慮到預(yù)測因素的合理性，研究人員從多個(gè)角度使用不同的影響因素預(yù)測原油價(jià)格波動。一些研究依賴基本市場信息分析和預(yù)測原油價(jià)格波動。Stephane Dees等[5]將原油價(jià)格建模為原油庫存和需求、石油輸出國組織(OPEC)產(chǎn)量、生產(chǎn)者配額和產(chǎn)能的函數(shù)。周喜安等[6]分析了國際原油價(jià)格上漲原因，認(rèn)為是需求增加、庫存下降、OPEC保價(jià)等原因的共同作用。然而，考慮到原油價(jià)格波動受到金融資本、貨幣等因素的影響，研究人員開始基于原油市場金融化的信息來分析原油波動。韓冬炎[7]指出世界原油供求關(guān)系變化是最為重要的因素。Haugom E等[8]在預(yù)測模型中引入了商品市場指標(biāo)，包括VIX指數(shù)、交易量和未平倉利率，有效預(yù)測原油波動。

Robert F Engle等[9]提出一種混合頻率方法：GARCH-MIDAS模型。該模型具有兩個(gè)乘性成分：短期成分服從GARCH(1,1)過程，可能被以相同頻率觀察到的其他變量所豐富;而長期成分是較低頻率觀察到的平滑濾波器。對于單變量GARCH-MIDAS模型的文獻(xiàn)已經(jīng)非常普遍。Luc Bauwens等[10]在多變量環(huán)境中構(gòu)建了GARCH-MIDAS模型;Amendola A等[11]提出雙非對稱 GARCH-MIDAS模型，研究了波動率動力學(xué)中的非對稱性;Engle R F[12]提出GARCH-X模型，此模型在短期組件中考慮了其他外生變量。

文中要解決特定的問題，即考慮非對稱效應(yīng)GARCH-MIDAS模型是否對原油價(jià)格波動存在不同的影響,以及能否更好地預(yù)測原油價(jià)格波動。為此，考慮兩種非對稱效應(yīng)：

1)短期成分的非對稱。將標(biāo)準(zhǔn)GARCH-MIDAS模型中短期成分服從GARCH(1,1)修改為TGARCH(1,1)。

2)長期成分的非對稱。在兩處地方進(jìn)行了修改，即將原油價(jià)格波動因素的符號不對稱性作為附加的解釋因素，并賦予相應(yīng)符號不同的權(quán)重函數(shù)。

此外，文中在GARCH-MIDAS的短期成分中考慮額外的波動決定因素——原油波動率指數(shù)(OVX)，觀察在GARCH-MIDAS-X類模型中是否也存在非對稱效應(yīng)。

1 原油價(jià)格波動率預(yù)測的模型構(gòu)建

1.1 GARCH-MIDAS模型

構(gòu)建GARCH-MIDAS模型，并對原油價(jià)格波動建模，表示如下

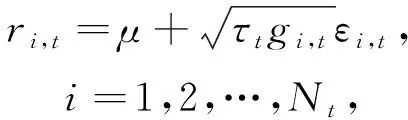
(1)

式中：ri,t——t月第i天時(shí)的對數(shù)收益率，是日度頻率數(shù)據(jù)；

Nt——t月份的交易天數(shù)；

εi,t——擾動項(xiàng)，服從條件標(biāo)準(zhǔn)正態(tài)分布，即εi,tΨi-1,t～N(0,1)，Ψi-1,t表示在t月份第i-1天可獲取的信息集。

顯然，波動率由τt和gi,t兩個(gè)成分組成,τt和gi,t分別為長期組成部分(每月頻率)和短期組成部分(每日波動)。

gi,t服從GARCH(1,1)過程

(2)

本著MIDAS回歸的精神，通過平滑已實(shí)現(xiàn)波動率來指定τt，

(3)

其中，K為低頻變量的最大滯后階數(shù)，φk(ω1,ω2)定義為MIDAS的權(quán)重方程，由Beta多項(xiàng)式進(jìn)行計(jì)算，

(4)

令ω2=1，使其權(quán)重函數(shù)為ω1的單調(diào)函數(shù)。式(1)～式(4)共同構(gòu)建了GARCH-MIDAS模型。

1.2 非對稱GARCH-MIDAS模型

將非對稱效應(yīng)納入到GARCH-MIDAS模型，短期成分將標(biāo)準(zhǔn)GARCH過程修改為TGARCH過程，長期成分將解釋變量的符號不對稱性作為附加的解釋變量。

1.2.1 短期成分的非對稱

在標(biāo)準(zhǔn)GARCH-MIDAS模型中考慮短期成分的非對稱效應(yīng)，構(gòu)建一個(gè)TGARCH-MIDAS模型，以包含非對稱效應(yīng)的短期影響，定義如下

βgi-1,t，

(5)

其中α>0,β>0,α+β+γ/2<1且E(gi,t)=1，1{}為指示函數(shù)，即1{ri-1,t<0}=1時(shí)為負(fù)收益，1{ri-1,t<0}=0時(shí)為正收益。

1.2.2 長期成分的非對稱

對長期成分的MIDAS回歸考慮非對稱效應(yīng)，改進(jìn)后的方程為

(6)

其中，m為截距，θ+和θ-反映了非對稱效應(yīng)，φk(ω)+和φk(ω)-為加權(quán)函數(shù)，文中使用Beta函數(shù)作為權(quán)重函數(shù)，即

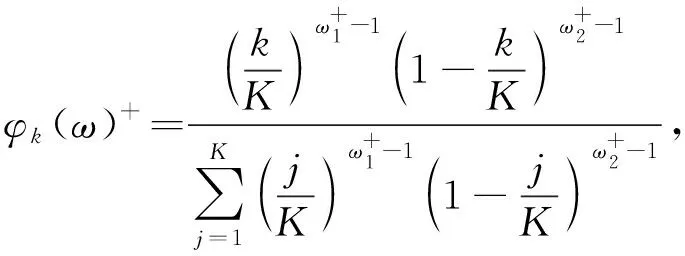
(7)

(8)

1.3 GARCH-MIDAS-X模型

將短期成分?jǐn)U展到一些額外的波動決定因素，這些因素的頻率應(yīng)與對數(shù)收益率ri,t的頻率相同，能夠使我們跳出經(jīng)典的GARCH-MIDAS框架，在式(2)和式(5)中包含“-X”部分，短期成分將分別修改為：

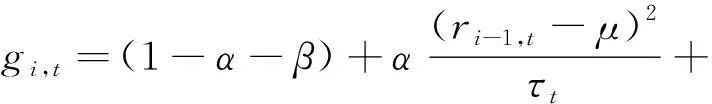
βgi-1,t+z·(Xi-1,t-E(Xi-1,t))，

(9)

βgi-1,t+z·(Xi-1,t-E(Xi-1,t))。

(10)

E(Xi-1,t)表示該因素在t周期內(nèi)到第i-1天的時(shí)間跨度內(nèi)的均值，假設(shè)z≥0,Xi,t≥0，且Xi,t是平穩(wěn)的，E(Xi,t)<∞，當(dāng)短期成分是式(10)時(shí)，這樣假設(shè)可以保證gi,t>0，且修改后的短期成分的無條件期望仍然為1。

文中模型共有8種，GARCH-MIDAS模型及其擴(kuò)展模型的短期成分和長期成分公式見表1。

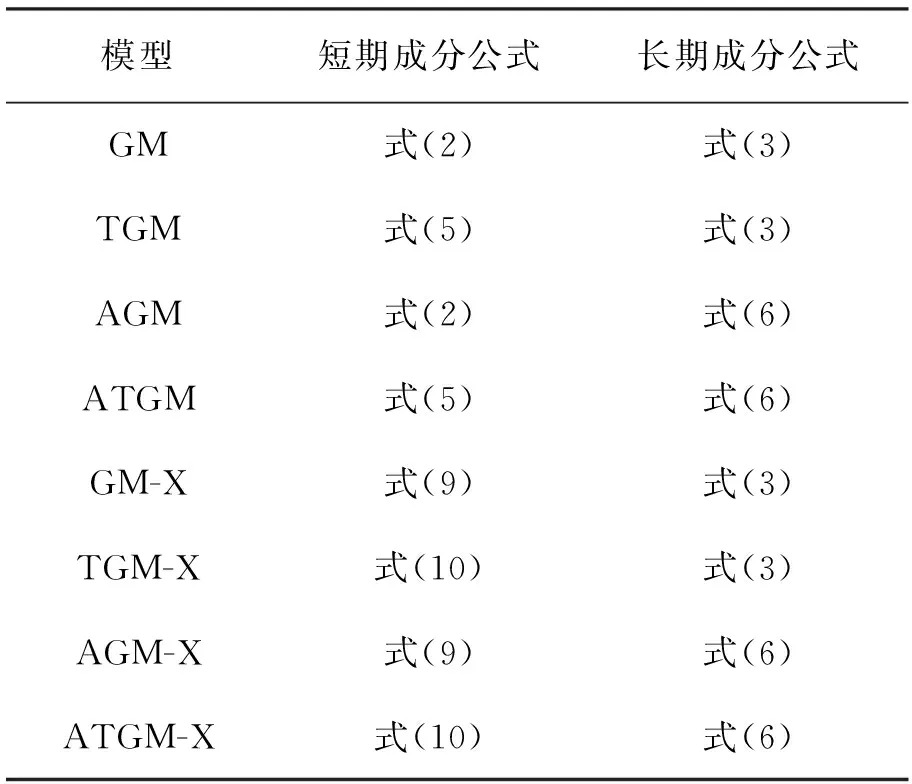
表1 GARCH-MIDAS模型及其擴(kuò)展模型的結(jié)構(gòu)

1.4 模型評價(jià)

通過模型置信集檢驗(yàn)(MCS)比較了非對稱GARCH-MIDAS模型和標(biāo)準(zhǔn)GARCH-MIDAS模型的性能，最后使用損失函數(shù)衡量不同模型的預(yù)測精度，文中選擇以下兩個(gè)損失函數(shù)作為預(yù)測誤差標(biāo)準(zhǔn)：

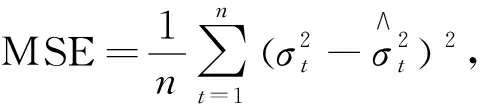
(11)

(12)

式中：n——波動率預(yù)測的總數(shù)量;

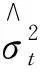
Yanran Ma等[13]指出損失函數(shù)無法提供有關(guān)模型之間的預(yù)測損失差異是否具有統(tǒng)計(jì)學(xué)意義的信息，因此，文中采用MCS檢驗(yàn)。MCS檢驗(yàn)的優(yōu)點(diǎn)為不需要指定基準(zhǔn)模型，在模型的整個(gè)集合中刪除性能最差的模型，直到在α顯著性水平上不再拒絕相同預(yù)測精度的零假設(shè)，生存下來的模型集為最優(yōu)模型集。文中采用檢驗(yàn)零假設(shè)的統(tǒng)計(jì)量為TSQ，

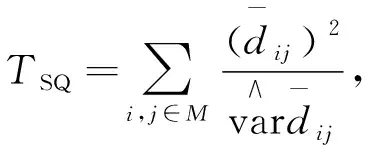
(13)

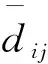
2 原油價(jià)格波動率預(yù)測的實(shí)證分析

2.1 數(shù)據(jù)

文中實(shí)證分析主要應(yīng)用于代表國際原油價(jià)格水平的西得克薩斯輕質(zhì)原油現(xiàn)貨價(jià)格(WTI)，計(jì)算其對數(shù)收益率(ri,t)和已實(shí)現(xiàn)波動率(RV)；考慮的原油價(jià)格波動因素為代表原油供給的歐佩克原油產(chǎn)量(OPEC)和代表原油庫存水平的美國原油商業(yè)庫存(USI)，考慮的額外市場活動變量為代表未來30 d原油市場預(yù)期波動程度的原油波動率指數(shù)(OVX)，OVX由美國芝加哥期權(quán)交易所(CBOE)推出。

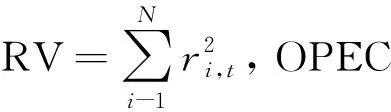
WTI對數(shù)收益率、WTI已實(shí)現(xiàn)波動率、OVX指數(shù)、OPEC原油產(chǎn)量以及美國原油商業(yè)庫存的均值、偏差、偏度、峰度和數(shù)據(jù)頻率見表2。

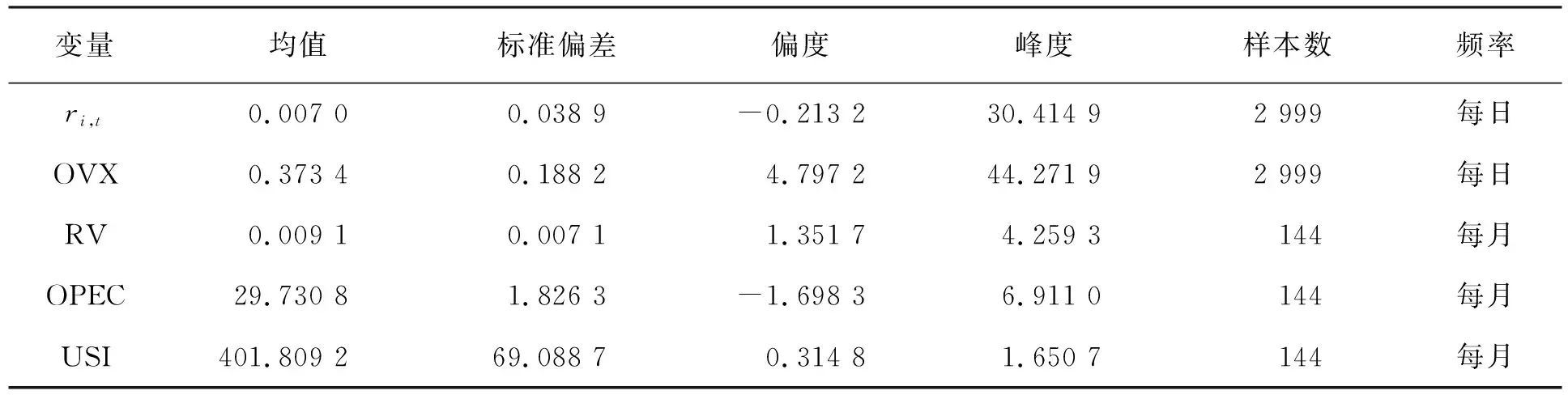
表2 描述性統(tǒng)計(jì)

WTI對數(shù)收益率和OPEC原油產(chǎn)量為左偏，其他變量均為右偏，并且除了美國原油商業(yè)庫存的其余變量峰度值均大于3，說明變量存在尖峰厚尾的特征。

對各變量進(jìn)行ARCH效應(yīng)檢驗(yàn)，結(jié)果見表3。

所有變量在滯后5、10、20 d的ARCH效應(yīng)檢驗(yàn)中具有1%的統(tǒng)計(jì)學(xué)顯著性，即變量存在ARCH效應(yīng)，因此使用GARCH類模型進(jìn)行建模是適當(dāng)?shù)摹?/p>

WTI對數(shù)收益和波動率的序列圖如圖1所示。

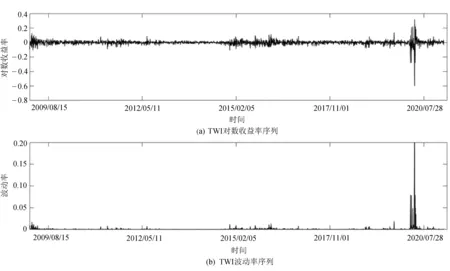
圖1 TWI的對數(shù)收益和波動率

從圖1可以看出，原油價(jià)格收益率的波動表現(xiàn)出聚集現(xiàn)象，與對原油的分析結(jié)果相符[14]。2020年出現(xiàn)樣本期內(nèi)的最大波動，反映出疫情對原油價(jià)格波動的重大影響。此外，2009年出現(xiàn)的波動較其他時(shí)期出現(xiàn)了小幅波動，說明金融危機(jī)時(shí)期對原油價(jià)格波動也產(chǎn)生了一定影響。

2.2 樣本內(nèi)估計(jì)結(jié)果

基于RV的不同模型參數(shù)估計(jì)值見表4。

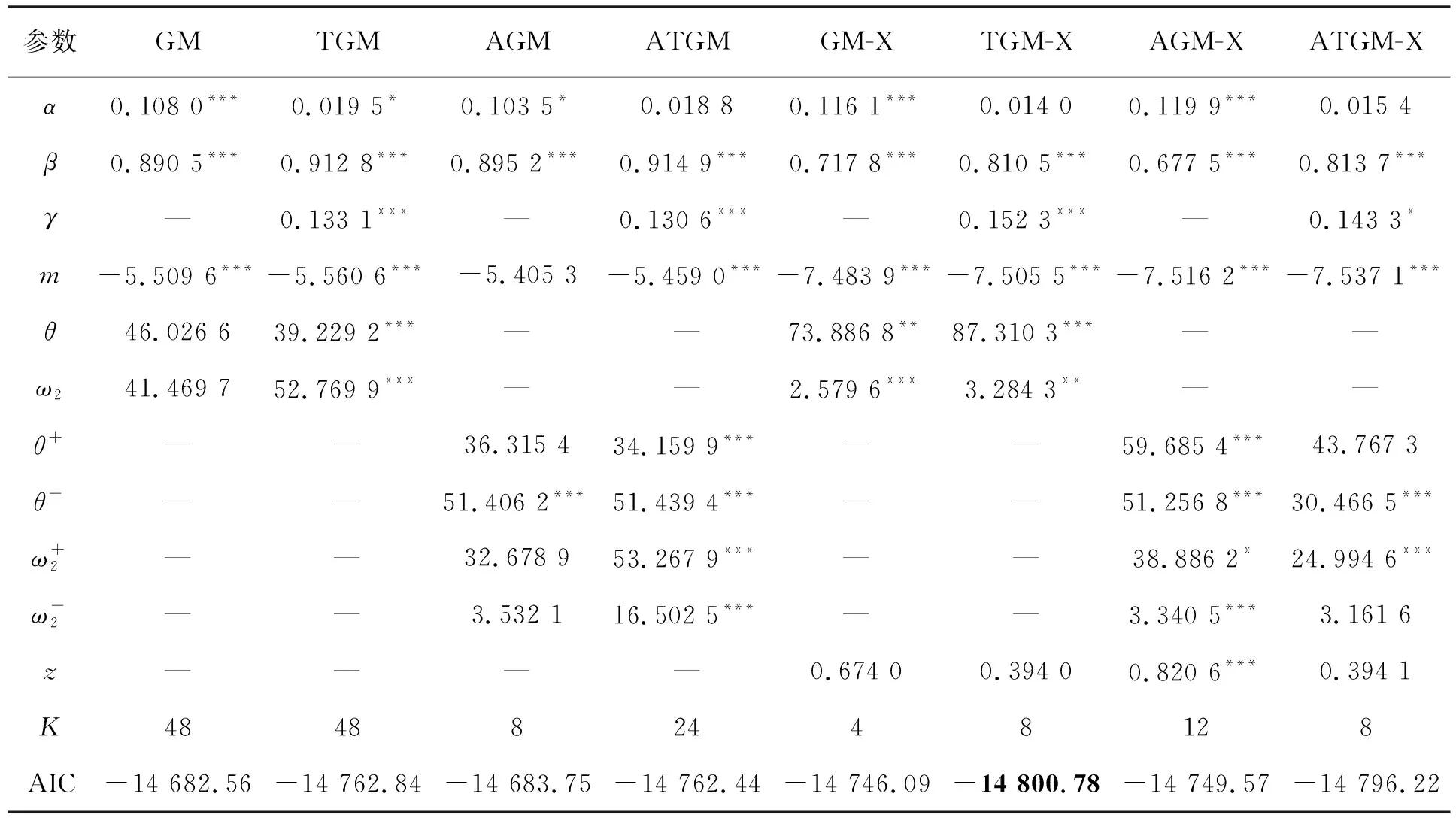
表4 基于RV的模型參數(shù)估計(jì)結(jié)果

其中α和β的總和接近于1，且β參數(shù)顯著性都為1%，說明存在強(qiáng)烈的波動持久性。首先考慮短期成分的非對稱性，短期波動的不對稱參數(shù)γ對原油市場價(jià)格波動性具有顯著影響，說明好信息和壞信息對原油波動的影響是不同的。此外，在長期成分的非對稱性中，θ+和θ-的顯著性不同，一般情況下，θ-的系數(shù)在1%水平下顯著,但θ+不顯著，表明壞信息會影響原油市場價(jià)格波動，而好消息對波動產(chǎn)生的影響較小。

另外，對各標(biāo)準(zhǔn)模型估計(jì)結(jié)果的絕對值進(jìn)行比較，在大多數(shù)情況下，|θ-|>|θ+|，表明在相同程度上，壞信息與好信息相比，會導(dǎo)致更高的原油市場價(jià)格波動，說明波動與壞信息之間的聯(lián)系要強(qiáng)于好信息。

診斷檢驗(yàn)使用赤池信息準(zhǔn)則(AIC)樣本選擇標(biāo)準(zhǔn)，相應(yīng)結(jié)果見表4下部，用黑體給出了最佳擬合模型，顯然，GARCH-MIDAS-X類模型都比GARCH-MIDAS類模型擬合得好，且考慮非對稱效應(yīng)的GARCH-MIDAS模型也都比標(biāo)準(zhǔn)GARCH-MIDAS模型擬合得更好。即修改后的模型在考慮短期成分和長期成分的非對稱效應(yīng)，并且將短期成分?jǐn)U展到額外的波動決定因素時(shí)，可以更好地捕捉原油市場價(jià)格波動的特征。

2.3 樣本外預(yù)測結(jié)果

通過樣本外預(yù)測直接比較不同模型的性能，驗(yàn)證考慮非對稱效應(yīng)是否可以提高原油價(jià)格波動的預(yù)測能力。通過向前移動滾動窗口，生成了2021年1月1日至2021年2月28日樣本期外的預(yù)測，共生成了38個(gè)日度預(yù)測。文中采用顯著性水平為α=0.25的模型置信集檢驗(yàn)來選擇最優(yōu)預(yù)測模型。

MSE和QLIKE的平均值見表5。

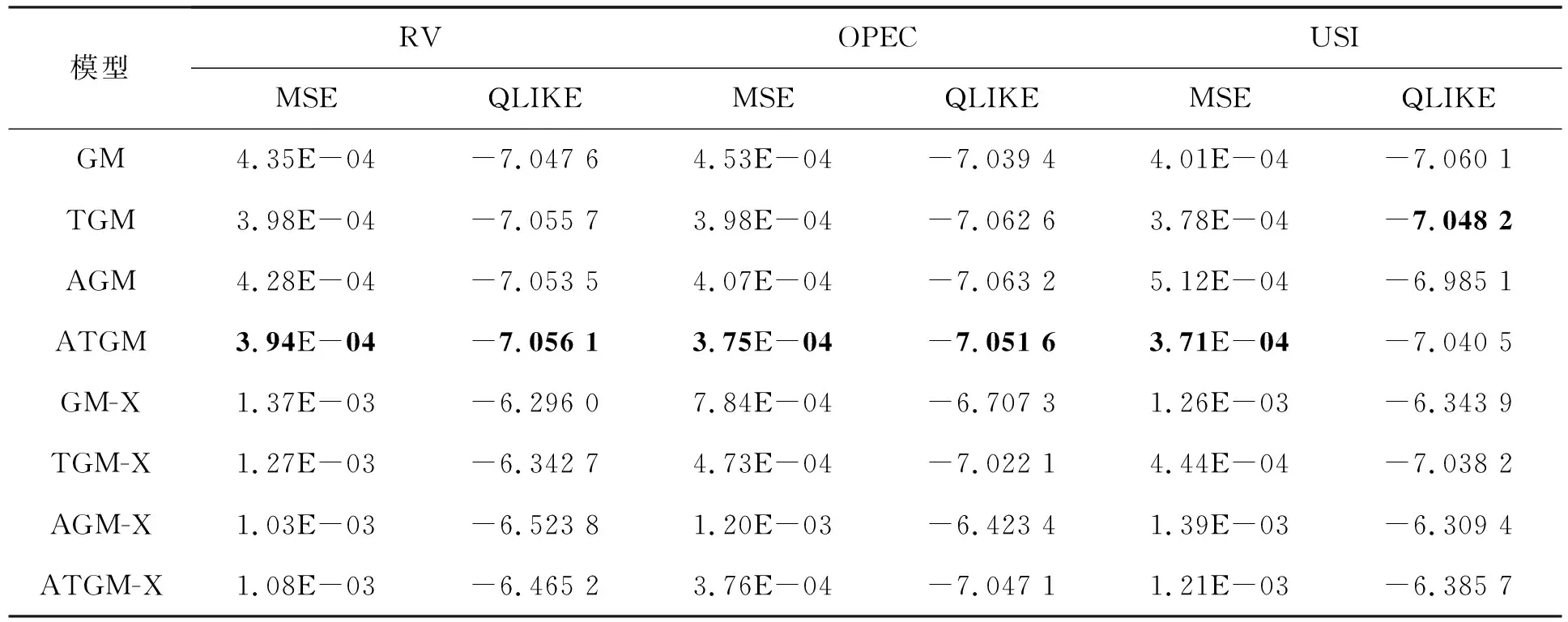
表5 樣本外預(yù)測的平均MSE和QLIKE

確定了在顯著性水平上通過MCS檢驗(yàn)的最佳模型。結(jié)果顯示，最優(yōu)模型一般為ATGM。在GM類模型中最低的MSE和QLIKE都來自考慮非對稱效應(yīng)的模型，同樣，在考慮額外波動因素OVX的GM-X類模型中也是如此。可以得到考慮非對稱效應(yīng)的GARCH-MIDAS比標(biāo)準(zhǔn)GARCH-MIDAS模型會產(chǎn)生更高預(yù)測性能的結(jié)論，這一結(jié)論表明,包括短期和長期成分的非對稱效應(yīng)可以有助于預(yù)測原油市場價(jià)格波動。此外，只考慮短期成分非對稱效應(yīng)模型的MSE都小于只考慮長期成分非對稱效應(yīng)模型的MSE，說明短期不對稱性比長期不對稱性更能提高波動率模型的預(yù)測能力。

3 結(jié) 語

通過考慮短期成分和長期成分的非對稱效應(yīng)，并將短期成分?jǐn)U展到一些額外的波動決定因素，即考慮非對稱效應(yīng)的GARCH-MIDAS與GARCH-MIDAS-X共8個(gè)模型，分別用于建模和預(yù)測，預(yù)測了國際原油WTI價(jià)格的波動性，研究考慮非對稱效應(yīng)的模型是否可以達(dá)到更高的預(yù)測準(zhǔn)確性。通過實(shí)證研究得到了幾個(gè)重要的發(fā)現(xiàn)。首先，樣本內(nèi)估計(jì)結(jié)果表明，在GARCH-MIDAS模型中，非對稱效應(yīng)對原油價(jià)格波動存在顯著影響，且好消息和壞消息對WTI波動性影響是不同的，通常情況下，壞信息與波動之間的關(guān)聯(lián)要強(qiáng)于好信息。其次，在樣本外預(yù)測性能方面，MCS檢驗(yàn)結(jié)果表明，非對稱效應(yīng)GARCH-MIDAS模型優(yōu)于標(biāo)準(zhǔn)GARCH-MIDAS模型，在預(yù)測波動率模型方面具有優(yōu)越的性能，在GARCH-MIDAS-X類模型中也是如此。并且發(fā)現(xiàn)對于波動率模型預(yù)測能力的提高，更多的應(yīng)該歸因于短期成分的非對稱效應(yīng)。