變式教學(xué) 讓課堂煥發(fā)生機

陳曉燕

(江蘇省如皋市實驗初中 226500)

數(shù)學(xué)概念的抽象性及數(shù)學(xué)問題的復(fù)雜性要求學(xué)生能靈活運用數(shù)學(xué)知識和技能解決問題，這就要求在數(shù)學(xué)課堂上要不斷變化條件進(jìn)行變式教學(xué)，使學(xué)生能適應(yīng)各種條件下的問題解決方式，透過現(xiàn)象抓住本質(zhì)，鍛煉思維能力.變式教學(xué)是建立在教師對教材和教學(xué)目標(biāo)的透徹理解以及準(zhǔn)確把握的基礎(chǔ)上，依據(jù)具體學(xué)情，為了幫助學(xué)生更加全面地理解數(shù)學(xué)知識，做出的合理變化練習(xí)與講解.但是數(shù)學(xué)課堂上仍然能有部分教師就題講題，教學(xué)方法毫無變化，使學(xué)生逐漸厭倦課堂，產(chǎn)生懼怕數(shù)學(xué)的情緒，為了能更有效地提高課堂效率，本文選取了“變式教學(xué)”的幾種典型方法同大家探討.

一、變式練習(xí)之變圖形

圖形題是數(shù)學(xué)學(xué)科中的常見題也是必考題，圖形的種類豐富，條件也是千變?nèi)f化，是讓很多學(xué)生頭疼的一類題型，因此這類題型需要教師能歸納總結(jié)各種變化類型，進(jìn)行變式練習(xí)，幫助學(xué)生抓住本質(zhì)，以“不變”應(yīng)“萬變”.

1.圖形和條件不變，改變思考方法得到相同的結(jié)論.

例1如圖1，∠A和∠D相等，∠B和∠E相等，且C、F在AD上，AF=DC，可以證明AB=DE嗎？

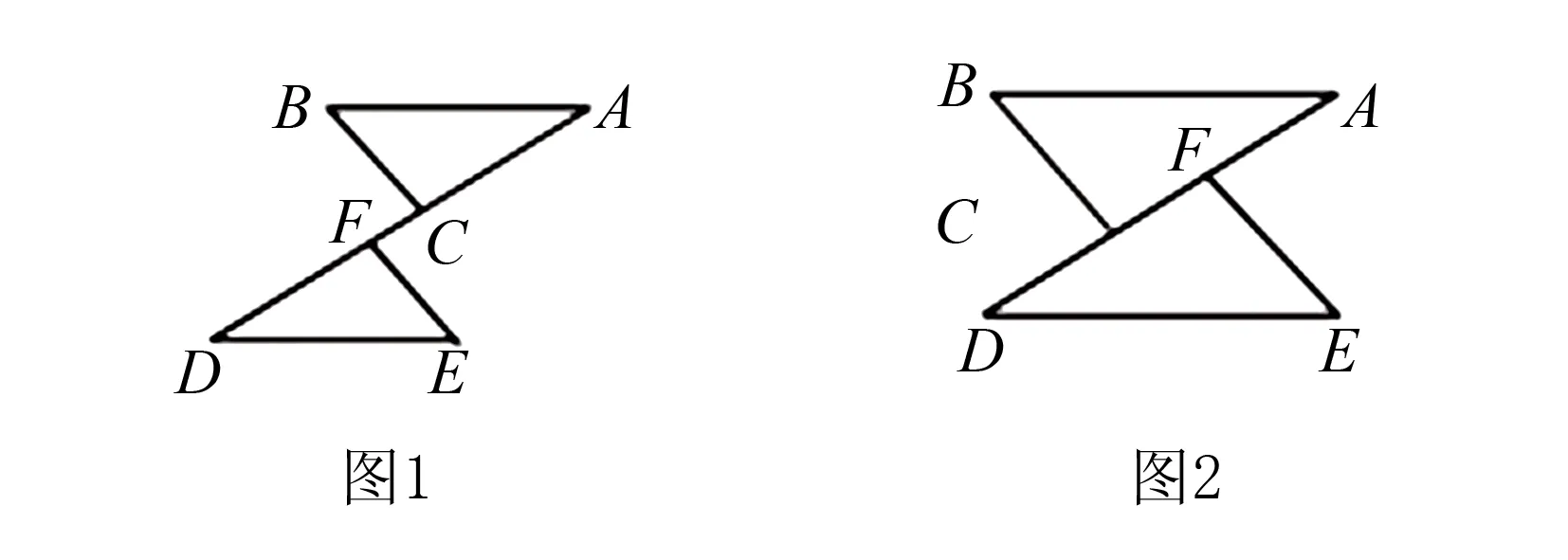
根據(jù)圖1進(jìn)行了圖2的變式練習(xí)，當(dāng)圖形和已知條件都沒有變化的情況下,結(jié)論也沒有變，那么學(xué)生就可以根據(jù)圖1的證明方法進(jìn)行方法的遷移運用，這也是考察和檢驗了學(xué)生對這一知識點的真正掌握情況，實現(xiàn)了知識的活學(xué)活用，學(xué)會了知識的遷移.

2.條件不變，變化圖形和結(jié)論.

例2如圖3，在△ABC中，AB=AC，∠BAC=90°，直線MN過點A，BD⊥MN于D，EC⊥MN于E.當(dāng)MN在△ABC外部時，證明DE、DB、CE的數(shù)量關(guān)系.

當(dāng)所給的條件不變，我們將圖形進(jìn)行一定的變化，考察學(xué)生能使用同樣的證明方法進(jìn)行求解.如圖4、圖5，在其他條件都不變的情況下，要求學(xué)生同樣證明圖3提出的問題，證明數(shù)量關(guān)系.

數(shù)學(xué)圖形的變化我們無法窮盡，但是教師在教學(xué)中通過變式練習(xí)，使學(xué)生能感受萬變不離其宗的本質(zhì)，在變與不變中，感受數(shù)學(xué)的神奇和奧秘，鍛煉思維，提升學(xué)習(xí)能力，從懼怕數(shù)學(xué)到樂于探索學(xué)習(xí)，實現(xiàn)學(xué)習(xí)數(shù)學(xué)的可持續(xù)發(fā)展.

二、變式練習(xí)之變結(jié)論

數(shù)學(xué)試題中學(xué)生經(jīng)常會疑惑同樣的試題條件，卻出現(xiàn)了不同的結(jié)論，如果沒有充分的變式練習(xí)，學(xué)生常常會受制于思維限制，一成不變的將答案進(jìn)行遷移，發(fā)生錯誤.因此教師要在不改變題目本質(zhì)的情況下，變化結(jié)論，引導(dǎo)學(xué)生進(jìn)行思考，預(yù)防學(xué)生可能發(fā)生的錯誤，跳出陷阱，增強學(xué)生學(xué)習(xí)的自信心，激發(fā)學(xué)習(xí)興趣，讓課堂充滿活力.

例3(分層收費問題)為了引導(dǎo)居民能節(jié)約用水，某市采用分段收費的方式進(jìn)行價格調(diào)控：每戶居民每月用水低于5立方米時，按照基礎(chǔ)價格收費；超過5立方米時，超過的部分要在原有基礎(chǔ)價格之上加價收費.該市居民4、5月份的用水量和水費如下，求該市居民的兩種水費價格.

月份用水量/立方米水費/元48225927

這類題型學(xué)生并不陌生，類似出租車收費、電費、燃?xì)馐召M等都有相似的特征，在實際生活中的運用也非常廣泛，因此如何讓學(xué)生熟練掌握，也體現(xiàn)了學(xué)習(xí)數(shù)學(xué)知識的應(yīng)用性.為此，筆者作了如下的變式練習(xí)：

變式一該市某戶居民7月份用水量為30立方米，該戶7月份應(yīng)交水費多少錢？

變式二該市某戶居民6月份交水費67元，該戶7月份的用水量為多少立方米？

本例中通過變式練習(xí)，學(xué)生熟練使用了同一條件求解不同問題的方法，靈活運用不同變量之間的數(shù)量關(guān)系，使高階思維得到了進(jìn)一步訓(xùn)練，知識體系更加完善.變式練習(xí)的目的是為了學(xué)生能用最少的時間，最有效的方式，能夠迅速掌握同一類型的練習(xí)，減少了學(xué)生亂撒網(wǎng)卻收效甚微的現(xiàn)象，在變式練習(xí)中進(jìn)行自我反思，不斷總結(jié)，不斷提升思維能力.也正是因為教師精心的設(shè)計，激發(fā)了思維的碰撞，讓原本乏味的課堂充滿變化，成為學(xué)生期待的探索之旅.

三、變式練習(xí)之變條件

幾何證明題需要學(xué)生發(fā)揮想象和預(yù)判能力，是對學(xué)生空間思維的一大挑戰(zhàn)，也是很多學(xué)生“談之色變”的一類題型，常常讓學(xué)生摸不著頭緒，非常煩惱.幾何證明題種類繁多，對它的訓(xùn)練不能建立在題海戰(zhàn)術(shù)的基礎(chǔ)上，要充分利用好一類題型進(jìn)行多種變化的訓(xùn)練，使學(xué)生能熟知對不同的條件，如何采用類似的證明方法進(jìn)行解決.

例4(結(jié)論不變，改變條件進(jìn)行圖形判定)如圖6，在ABCD中，AE⊥BD,CF⊥BD，垂足分別是E和F.請證明四邊形AECF是平行四邊形.

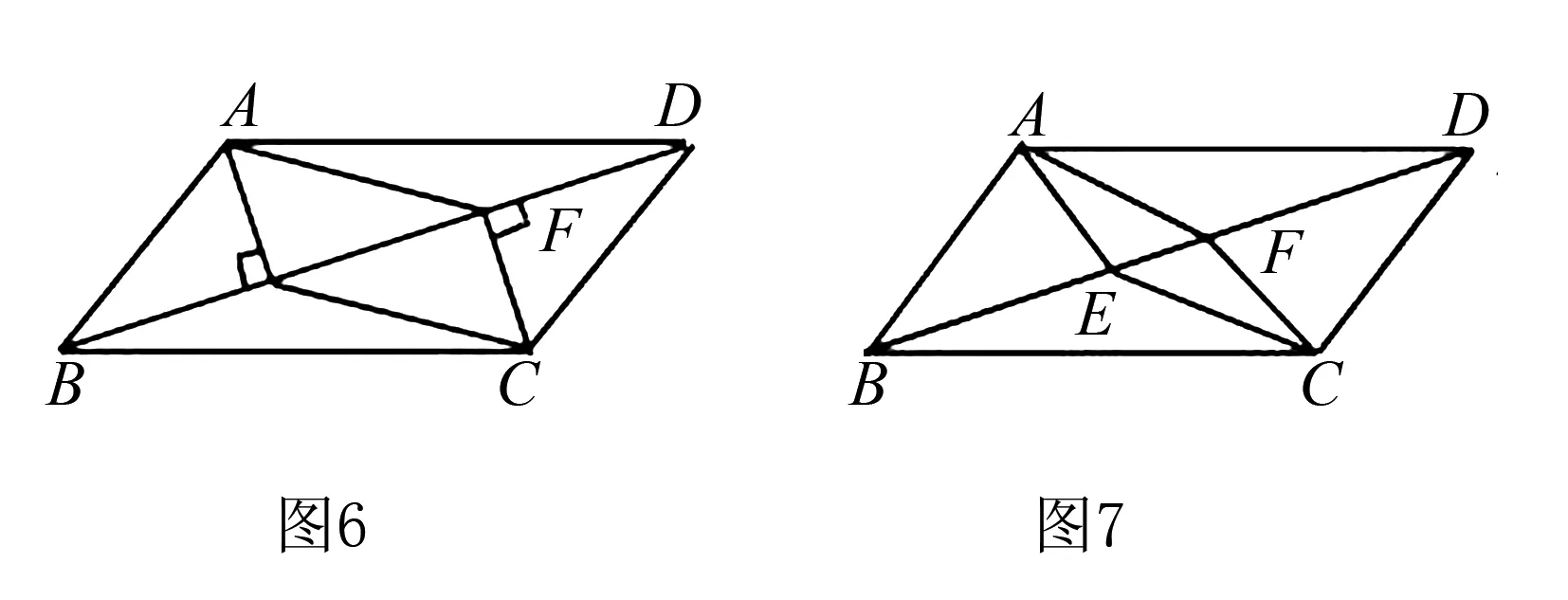
進(jìn)行圖形的判定需要學(xué)生突破思維定勢，大膽想象，靈活運用所學(xué)知識，但是往往有些學(xué)生面對這類問題會不知所措，陷入困境，無法將已知條件和未知的問題相結(jié)合，找不到突破點.這充分暴露了在平時的教學(xué)中，沒有進(jìn)行充分的變式訓(xùn)練，使思維呈現(xiàn)單向性，面對復(fù)雜的題型不能進(jìn)行有效的分解，無法找到突破口.針對這樣的問題，筆者對于圖形判定題進(jìn)行了條件變式的練習(xí)：

變式一把原題中“AE⊥BD，CF⊥BD，垂足分別為E和F”變成如圖7，E、F是BD上的兩點，并且BE=CF，證明四邊形AECF是平行四邊形.

變式二把原題中“AE⊥BD，CF⊥BD，垂足分別為E和F”變成如圖7，E、F是BD上的兩點，BF=CE，證明四邊形AECF是平行四邊形.

變式三把原題中“AE⊥BD，CF⊥BD，垂足分別為E和F”變成如圖7，E、F是BD上的兩點，并且AE∥CF,證明四邊形AECF是平行四邊形.

通過這樣的變式練習(xí)，不僅使學(xué)生充分掌握了判定圖形的證明方法，而且使學(xué)生充分認(rèn)識到學(xué)會一種方法遠(yuǎn)比會做一道題來得重要，學(xué)習(xí)數(shù)學(xué)的目的不是為了做題而做題，而是在做題中學(xué)會總結(jié)規(guī)律和方法，走出死記硬背，刻板模仿的誤區(qū)，真正掌握學(xué)習(xí)數(shù)學(xué)的科學(xué)方法，體會學(xué)習(xí)數(shù)學(xué)的樂趣.