ANSI B92.1b美標漸開線花鍵配合側隙及跨棒距計算

孫鵬

（山東中潤液壓機械有限公司，山東臨沂 276700）

0 引言

ANSI B92.1b-1996 漸開線花鍵為雙徑節漸開線花鍵，雙徑節漸開線花鍵的徑節P與米制模數漸開線花鍵中的模數m的關系為P=25.4/m。雙徑節可以被理解為2個模數，且徑節P與殘余徑節PS之間的關系為PS=2P，其中徑節P控制花鍵的分度圓直徑、基圓直徑、齒厚、齒槽寬，而殘余徑節PS控制花鍵的大徑、小徑，雙徑節漸開線花鍵齒形為低短齒，由于此類花鍵參數繁多、概念抽象，初次接觸此類花鍵的工程師在設計時常常覺得無從下手，掌握標準中花鍵設計原理，會對工作開展大有益處。

標準中花鍵類別根據分度圓壓力角分為30°、37.5°、45°等3類，根據齒根結構分為平齒根和圓角齒根2類，而37.5°和45°壓力角花鍵只有圓角齒根結構，30°壓力角花鍵又分為平齒根和圓角齒根2類，其中30°平齒根又分為齒側配合和大徑配合2種，而圓角齒根結構只能是齒側配合。其中30°壓力角平齒根齒側配合花鍵在液壓元件設計當中最為常用，本文將重點介紹此類花鍵的設計計算。

1 30°壓力角平齒根齒側配合花鍵基本參數的符號及計算公式

30°壓力角平齒根齒側配合花鍵基本參數的計算公式包括：分度圓直徑D=N/P，基圓直徑Db=D·cos 30°，最小作用齒槽寬Svmin=π/（2P），最大作用齒槽寬Svmax=Svmin+f·m，最小實際齒槽寬Smin=Svmin+f·λ，最大實際齒槽寬Smax=Svmin+f·（m+λ），最大作用齒厚tvmax=π/（2P）-es，最小作用齒厚tvmin=tvmax-f·m，最大實際齒厚tmax=tvmax－f·λ，最小實際齒厚tmin=tvmax－f·(m+λ)。式中：N為花鍵齒數；m為機械加工誤差，定義為外花鍵實際齒厚與內花鍵實際齒槽寬的加工誤差[1]；λ為綜合公差，定義為花鍵的齒距累積誤差、齒形誤差、齒向誤差對花鍵配合作用側隙的綜合影響帶來的誤差[1]，計算公式如表1中所述[1]；f為精度系數，花鍵共分為4個精度等級，分別為4、5、6、7，其中5級精度系數為1，與5級相比，4級要求更高，4級系數為0.71，6、7精度要求依次降低，6級系數為1.4，7級系數為2.0[1]；es為最小作用側隙，此標準中的花鍵齒側配合采用基孔制，即用改變外花鍵作用齒厚上偏差的方法實現不同的配合，有4種偏差可選，分別為h、f、e、d，h偏差對應的es=0，f偏差對應的es=D0.41/1220，e偏差對應的es=D0.41/610，d偏差對應的es=D0.44/380[1]。

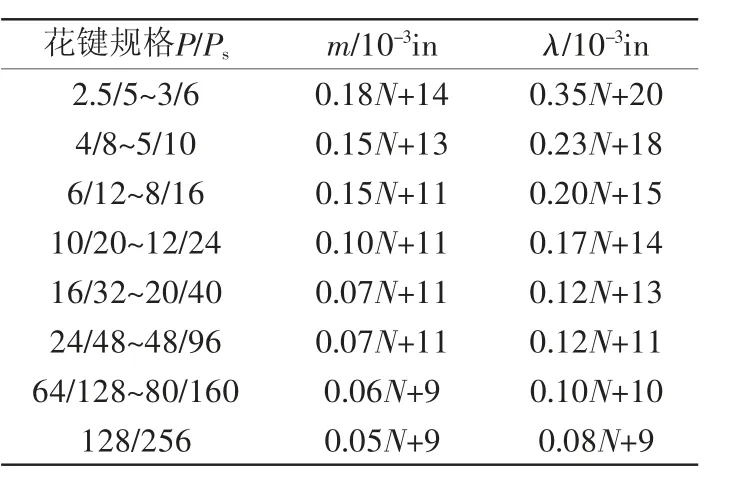
表1 不同規格的花鍵對應的m及λ值計算公式

2 花鍵配合側隙的概念及公差帶介紹

花鍵配合側隙分為花鍵配合作用側隙與實際側隙。作用側隙Cv的概念為內花鍵作用齒槽寬減去與之配合的外花鍵作用齒厚所得差即為作用側隙[2]。實際側隙C的概念為內花鍵實際齒槽寬減去與之配合的外花鍵實際齒厚所得差即為實際側隙[2]。內外花鍵配合公差帶示意圖如圖1所示，此示意圖為5級精度花鍵配合公差帶示意圖，其它精度等級公差帶帶寬需要乘以相應的精度系數f。

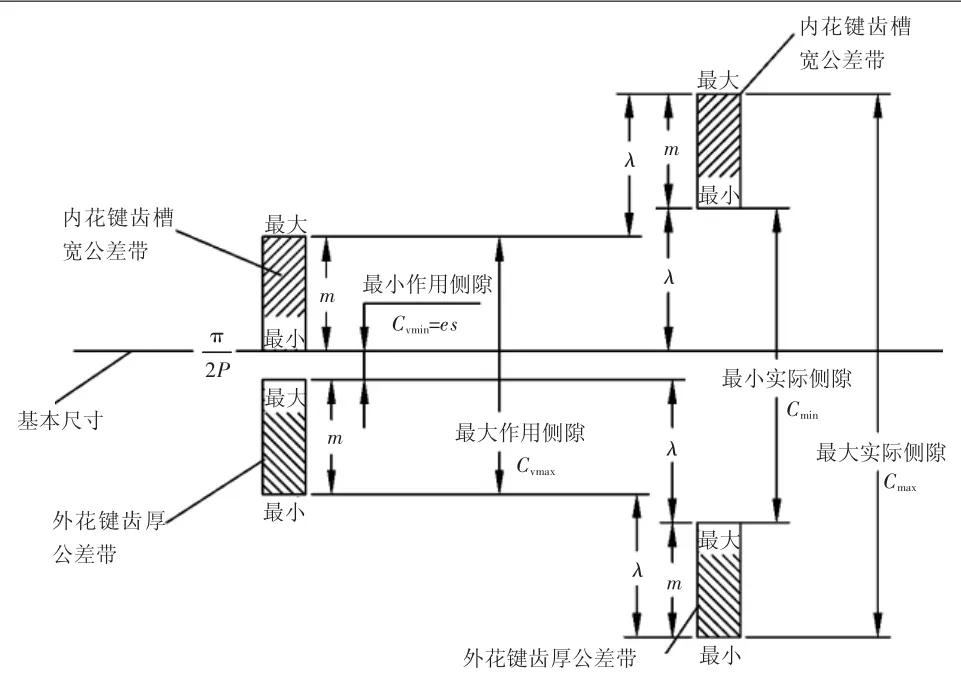
圖1 齒厚齒槽寬公差帶示意圖

圖1中，Cvmin為花鍵配合最小作用側隙（即es），標準中指出根據花鍵配合安裝條件計算最小作用側隙的計算公式[1]為

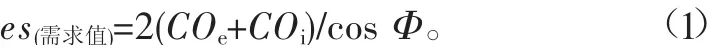
式中：COe為外花鍵軸線與花鍵軸安裝中心線的偏心值；COi為內花鍵軸線與花鍵套安裝中心線的偏心值；Φ為花鍵漸開線齒廓在分度圓上的壓力角，本文中Φ=30°。根據不同外花鍵作用齒厚偏差逐個計算es值，與es(需求值)比較，要求所選的外花鍵作用齒厚偏差所計算的es值須大于es(需求值)[1]。

圖1中：Cvmax為花鍵配合最大作用側隙，根據圖1中公差帶圖可知Cvmax=Svmax-tvmin=es+f·(m+m)；Cmin為花鍵配合最小實際側隙，根據圖1中公差帶圖可知Cmin=Smin-tmax=es+f·(λ+λ)；Cmax為花鍵配合最大實際側隙，根據圖1中公差帶圖可知Cmax=Smax-tmin=es+f·(m+λ)+f·(m+λ)。

3 外花鍵跨棒距及內花鍵棒間距的計算

3.1 外花鍵跨棒距計算公式介紹

標準中給出以下公式[1]：

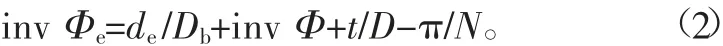
式中：Φe為花鍵漸開線齒廓在量棒圓心所在圓上的壓力角；de為量棒直徑；Db為基圓直徑；D為分度圓直徑；Φ為花鍵漸開線齒廓在分度圓上的壓力角；t為分度圓齒厚；N為花鍵齒數。

由式（2）可以求出花鍵漸開線齒廓在量棒圓心所在圓上的壓力角Φe。根據漸開線性質可知，量棒圓心所在圓直徑為Db/cos Φe，已知量棒圓心直徑和量棒直徑，可得出外花鍵跨棒距公式：

偶數齒時為

3.2 內花鍵棒間距計算公式介紹

標準中給出以下公式[1]：

式中：Φi為花鍵漸開線齒廓在量棒圓心所在圓上的壓力角；di為量棒直徑；s為花鍵分度圓齒槽寬。

由式（6）可以求出花鍵漸開線齒廓在量棒圓心所在圓上的壓力角Φi，根據漸開線性質可知，量棒圓心所在圓直徑為Db/cos Φi，已知量棒圓心所在圓心直徑和量棒直徑，可得出內花鍵棒間距公式：

偶數齒時為

奇數齒時為

標準中規定30°壓力角漸開線內花鍵的量棒直徑計算公式[1]為

4 齒厚公差與跨棒距公差之間的關系推導

4.1 外花鍵齒厚公差與跨棒距之間關系推導（如圖2）

圖2 外花鍵齒厚與跨棒距的關系

圖2中：x為兩條過測量棒圓心的漸開線法線距離；Δt為外花鍵齒厚變化量；ΔMe為齒厚變化導致的跨棒距變化量；Φ為花鍵漸開線齒廓在分度圓上的壓力角；Φe為花鍵漸開線齒廓在量棒圓心所在圓上的壓力角。

根據圖中幾何關系可知，x=（ΔMe/2）·sin Φe，且x=（Δt/2）·cos Φ。因此得出ΔMe·sin Φe=Δt·cos Φ，即ΔMe/Δt=cos Φ/sin Φe。

用Ke表示齒厚變化導致跨棒距變化的影響系數，當花鍵為偶數齒時有

當花鍵為奇數齒時有

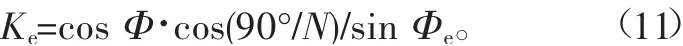
4.2 內花鍵齒槽寬公差與棒間距之間關系推導（如圖3）

圖3中：x為兩條過測量棒圓心的漸開線法線距離；Δs為內花鍵齒槽寬變化量；ΔMi為齒槽寬變化導致的棒間距變化量；Φ為花鍵漸開線齒廓在分度圓上的壓力角；Φi為花鍵漸開線齒廓在量棒圓心所在圓上的壓力角。

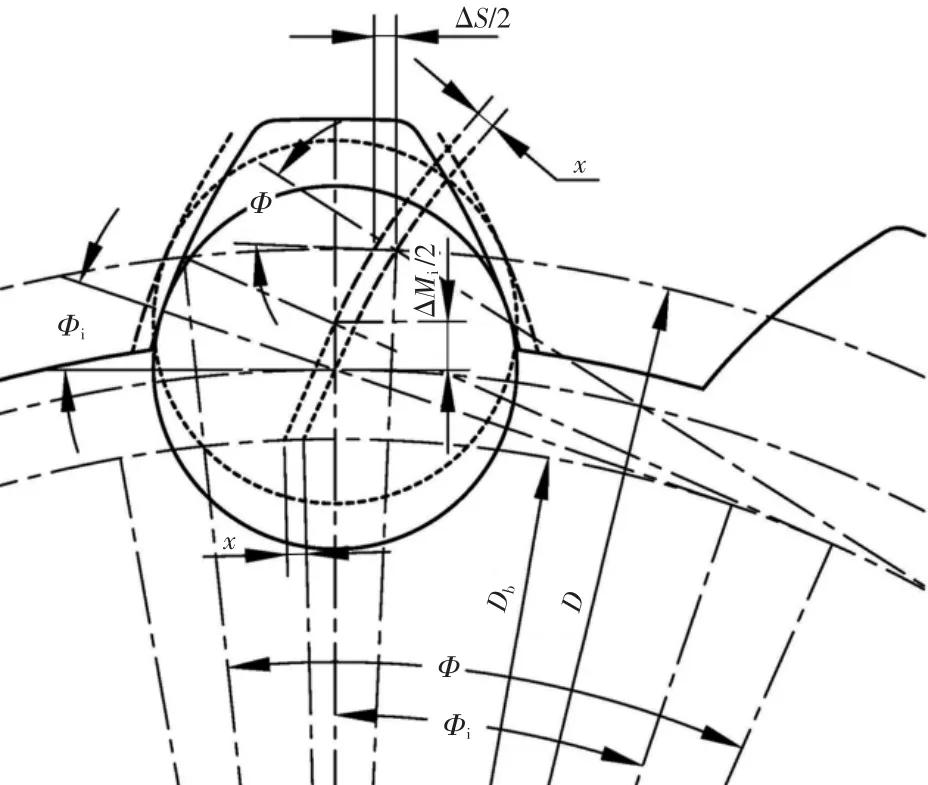
圖3 內花鍵齒槽寬與棒間距的關系

根據圖中幾何關系可知，x=（ΔMi/2）·sin Φi，且x=（Δs/2）·cos Φ。因此得出（ΔMi/2）·sin Φi=（Δs/2）·cos Φ，即ΔMi/Δt=cos Φ/sin Φi。

用Ki表示齒槽寬變化導致棒間距變化的影響系數，當花鍵為偶數齒時，

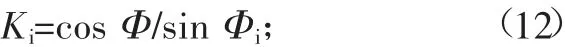
當花鍵為奇數齒時，

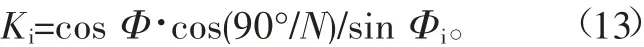
通過以上推導，得出了齒厚變化導致跨棒距變化及齒槽寬變化導致棒間距變化的影響系數，因此可以在求得齒厚、齒槽寬公差的情況下用以上幾個基本公式進一步求出跨棒距、棒間距的公稱值及公差要求。

5 計算實例

已知一對平齒根齒側配合花鍵參數，花鍵齒數N=15，壓力角Φ=30°，徑節P=16，花鍵精度等級為6級，花鍵軸分度圓相對于軸中心跳動要求為0.02 mm，內花鍵分度圓相對于軸中心跳動要求為0.02 mm，要求連接為可軸向滑動配合，求花鍵側隙、跨棒距及棒間距。

5.1 側隙計算

分度圓直徑D=N/P=25.4×15÷16=23.8125 mm。基圓直徑Db=D·cos 30°=23.8125·cos 30°=20.622 mm。根據已知花鍵參數，查表1計算m、λ值：機械加工誤差m=25.4×(0.07N+11)×0.0001=25.4×(0.07×15+11)×0.0001=0.0306 mm；綜合誤差λ=25.4×(0.12N+13)×0.0001=25.4×(0.12×15+13)×0.0001=0.0376 mm。根據式（1）計算最小作用側隙，得es（需求值）=（0.02+0.02）÷cos 30°=0.046 mm。

根據各類外花鍵作用齒厚偏差，來計算確定選擇哪種齒厚偏差能滿足最小側隙要求：d配合偏差es=D0.44/380=0.065 mm，e配合偏差es=D0.41/610=0.041 mm，f配合偏差es=D0.41/1220=0.02 mm，h配合偏差es=0 mm，由于需要采用間隙配合，應該選擇d級齒厚偏差，即es=0.065 mm。

最大作用齒厚tvmax=π/(2P)-es=25.4×3.1415/（2×16）-0.065=2.429 mm；最小作用齒槽寬Svmin=π/(2P)=25.4×3.1415/（2×16）=2.494 mm；花鍵精度為6級，精度系數f=1.4；最小實際齒厚tmin=tvmax-f·（m+λ）=2.429-1.4×（0.0306+0.0376）=2.333 mm；最大實際齒槽寬Smax=Svmin+f·（m+λ）=2.494+1.4×（0.0306+0.0376）=2.589 mm；最大實際側隙Cmax=Smax-tmin=2.589-2.333=0.256 mm；最大實際齒厚tmax=tvmax-f·λ=2.429-1.4×0.0376=2.376 mm；最小實際齒槽寬Smin=Svmin+f·λ=2.494+1.4×0.0376=2.546 mm；最小實際側隙Cmin=Smin-tmax=2.546-2.376=0.17 mm。

5.2 外花鍵跨棒距計算

根據式（5）計算外花鍵量棒直徑得de=25.4×1.92/P=25.4×1.92÷16=3.048 mm。標準壓力角漸開線函數值inv Φ=inv 30°=0.054。根據式（2）計算理論量棒中心所在圓的壓力角漸開線函數值，得inv Φe=de/Db+inv Φ+t/D-π/N=3.048÷20.622+0.054+2.494÷23.8125-3.1415÷15=0.097。式中t為理論分度圓齒厚,t=π/（2P）=25.4×3.1415/(2×16)=2.494 mm。通過反漸開線函數求出理論量棒中心所在圓的壓力角Φe=35.848°。根據式（11）計算齒厚變化導致跨棒距變化的影響系數，得Ke=cos Φ·cos(90°/N)/sin Φe=cos 30°×cos(90°÷15)/sin 35.848°=1.471。根據圖1可知：齒厚公差上差Δt上差=-f·λ=-1.4×0.0376=-0.0526 mm；齒厚公差下差Δt下差=-f·(m+λ)=-1.4×(0.0306+0.0376)=-0.0955 mm；跨棒距公差上差ΔMe上差=Ke·Δt上差=1.471×（-0.0526）=-0.077 mm；跨棒距公差下差ΔMe下差=Ke·Δt下差=1.471×（-0.0955）=-0.140 mm。根據式（2）計算最小實際齒厚狀態，量棒中心所在圓的壓力角漸開線函數值inv Φe=de/Db+inv Φ+t/D-π/N=3.048÷20.622+0.054+2.333÷23.8125-3.1415÷15=0.0901。式中t為最小實際齒厚tmin,已求出tmin=2.333 mm。通過反漸開線函數求出最小實際齒厚狀態，量棒中心所在圓的壓力角Φe=35.088°。根據式（4）計算得到最小實際齒厚狀態跨棒距Memin=Db·cos (90°/N)·sec Φe+de=20.622×cos(90°÷15) ×sec 35.088°+3.048=28.112 mm。跨棒距的公稱值Me=Memin-ΔMe下差=28.112-(-0.1404)=28.253 mm。因此外花鍵跨棒距設計值為28.253mm。

5.3 內花鍵棒間距計算

根據式（9）計算內花鍵量棒直徑得di=25.4×1.7280/P=25.4×1.728÷16=2.743 mm。標準壓力角漸開線函數值inv Φ=inv 30°=0.054。根據式（6）計算理論量棒中心所在圓的壓力角漸開線函數值，得inv Φi=inv Φ+s/D-di/Db=0.054+2.494÷23.8125-2.743÷20.622=0.025。式中，s為理論分度圓齒槽寬，s=π/（2P）=25.4×3.1415÷(2×16)=2.494 mm。通過反漸開線函數求出理論量棒中心所在圓的壓力角Φi=23.740°。根據式（13）計算齒槽寬變化導致棒間距變化的影響系數，得Ki=cos Φ×cos(90°/N)/sin Φi=cos 30°×cos(90°÷15)÷sin 23.740°=2.139。根據圖1可知：齒槽寬公差上差Δs上差=f·(m+λ)=1.4×(0.0306+0.0376)=0.0955 mm；齒槽寬公差下差Δs下差=f·λ=1.4×0.0376=0.0526 mm；棒間距公差上差ΔMi上差=Ki·Δs上差=2.139×0.0955=0.204 mm；棒間距公差下差ΔMi下差=Ki·Δs下差=2.139×0.0526=0.113 mm。根據式（6）計算最大實際齒槽寬狀態量棒中心所在圓的壓力角漸開線函數值，得inv Φi=inv Φ+s/D-di/Db=0.054+2.589÷23.8125-2.743÷20.622=0.0297。式中s為最大實際齒槽寬Smax，已求出Smax=2.589 mm。通過反漸開線函數求出最大實際齒槽寬狀態量棒中心所在圓的壓力角Φi=24.866°。根據式（8）計算最大實際齒槽寬狀態棒間距，得Mimax=Db·cos(90°/N)·sec Φi-di=20.622×cos(90°÷15) ×sec 24.866°-2.743=19.862 mm。棒間距的公稱值Mi=Mimax-ΔMi上差=19.862-0.204=19.658 mm。因此內花鍵棒間距設計值為19.658mm。

6 結語

本文參考ANSI B92.1的標準結構，通過推導跨棒距及齒厚的關系，進而得出設計花鍵參數需要給出的跨棒距公稱值及公差要求，給出齒厚、齒槽寬要求等重要參數的計算方法。