比例導(dǎo)引律在空間交會(huì)中的應(yīng)用研究

0 引 言

交會(huì)對(duì)接的制導(dǎo)控制一直是空間技術(shù)領(lǐng)域的研究熱點(diǎn)。國(guó)內(nèi)外有大量文獻(xiàn)對(duì)空間交會(huì)的制導(dǎo)控制進(jìn)行了研究[1~3]，其中大多基于動(dòng)力學(xué)規(guī)律對(duì)飛行器進(jìn)行預(yù)測(cè)和控制，控制效果較好，但其對(duì)導(dǎo)航設(shè)備的精度要求較高，需要克服慣性器件誤差的累積效應(yīng)。

比例導(dǎo)引是一種基于運(yùn)動(dòng)學(xué)規(guī)律進(jìn)行軌道控制的閉路制導(dǎo)控制方法，它使飛行器速度向量的旋轉(zhuǎn)角速度與目標(biāo)視線(xiàn)的旋轉(zhuǎn)角速度成正比，以達(dá)到消除視線(xiàn)轉(zhuǎn)率的目的，從而實(shí)現(xiàn)對(duì)目標(biāo)的準(zhǔn)確攔截[4,5]。由于視線(xiàn)參數(shù)測(cè)量相對(duì)簡(jiǎn)單，對(duì)慣性器件精度要求不高，且易于工程實(shí)現(xiàn)，因而在目標(biāo)攔截領(lǐng)域得到廣泛應(yīng)用[6,7]。文獻(xiàn)[8]和文獻(xiàn)[9]開(kāi)展了比例導(dǎo)引律在大氣層外攔截器應(yīng)用的研究，由于與空間交會(huì)過(guò)程不同，并未考慮近距離減速制動(dòng)過(guò)程的制導(dǎo)律設(shè)計(jì)。文獻(xiàn)[10]采用比例導(dǎo)引方式實(shí)現(xiàn)了空間交會(huì)控制，但在交會(huì)末段出現(xiàn)了視線(xiàn)角速度劇烈變化的現(xiàn)象，軌控發(fā)動(dòng)機(jī)頻繁開(kāi)啟。

本文對(duì)比例導(dǎo)引應(yīng)用于空間交會(huì)進(jìn)行研究，針對(duì)勻速接近段和減速制動(dòng)段分別提出了適應(yīng)固定推力的比例導(dǎo)引律，實(shí)現(xiàn)了較高的交會(huì)精度，有效減少了交會(huì)末段發(fā)動(dòng)機(jī)開(kāi)啟次數(shù)和燃料消耗，并對(duì)非機(jī)動(dòng)目標(biāo)和機(jī)動(dòng)目標(biāo)的適應(yīng)性進(jìn)行了仿真分析。本文研究的追蹤器安裝4臺(tái)軌控發(fā)動(dòng)機(jī)，可提供垂直于視線(xiàn)的4個(gè)方向的控制力，且推力為常值，可多次啟動(dòng)。

1 相對(duì)運(yùn)動(dòng)動(dòng)力學(xué)方程

首先定義視線(xiàn)坐標(biāo)系Oξηζ。原點(diǎn)O位于追蹤器質(zhì)心，Oξ軸與視線(xiàn)方向重合，Oη在軌道平面內(nèi)與Oξ軸垂直，Oζ軸垂直于Oξη平面。

設(shè)rM、rT分別表示追蹤器和目標(biāo)的地心矢量，r表示追蹤器指向目標(biāo)的相對(duì)矢量，r=rT-rM。追蹤器的相對(duì)運(yùn)動(dòng)矢量方程為

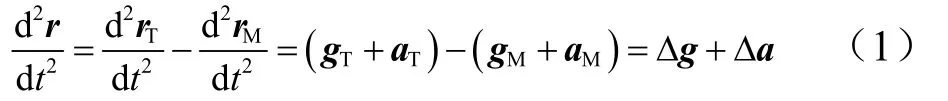
式中 Δg為作用在目標(biāo)和追蹤器上的引力加速度差。由于追蹤器和目標(biāo)間的距離相對(duì)地心距為小量，引力差為小量，且交會(huì)過(guò)程的時(shí)間較短，可忽略其對(duì)相對(duì)運(yùn)動(dòng)的影響，將Δg項(xiàng)略去；Δa為作用在目標(biāo)和追蹤器上的控制加速度差。不考慮目標(biāo)機(jī)動(dòng)時(shí)，ΔaT=0，則Δa=ΔaM。

設(shè)視線(xiàn)坐標(biāo)系相對(duì)于慣性坐標(biāo)系的轉(zhuǎn)動(dòng)角速度為ω，其在視線(xiàn)坐標(biāo)系上的3個(gè)分量分別為ωξ、ωη和ωζ，即ω=(ωξωηωζ)T。視線(xiàn)方向的角速度ωξ近似為零。矢量形式的相對(duì)運(yùn)動(dòng)動(dòng)力學(xué)方程為

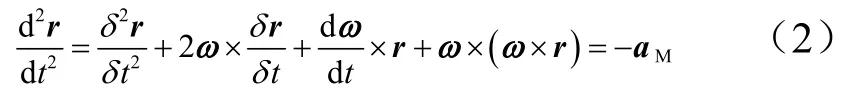
式中r=(r0 0)T。追蹤器的控制加速度在視線(xiàn)坐標(biāo)系的表示為aM=(aξ aη aζ)T。

式（2）可化簡(jiǎn)為標(biāo)量形式的相對(duì)運(yùn)動(dòng)動(dòng)力學(xué)方程：

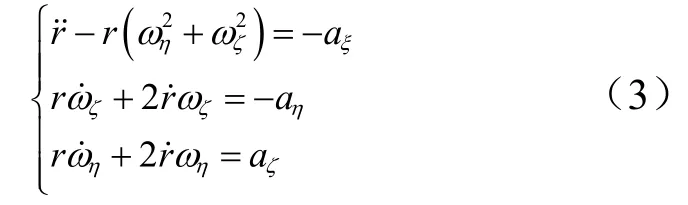
不進(jìn)行控制時(shí)，aξ=aη=aζ=0，對(duì)后兩式積分可得：

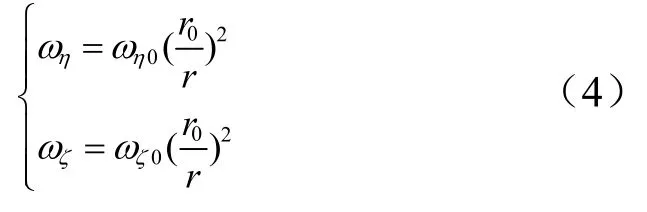
可見(jiàn)，如果對(duì)追蹤器不施加控制，視線(xiàn)角速率將隨著相對(duì)距離r的減小而不斷增大，無(wú)法滿(mǎn)足比例導(dǎo)引視線(xiàn)角速率收斂的要求。

2 比例導(dǎo)引律設(shè)計(jì)

將整個(gè)交會(huì)過(guò)程分為勻速接近段和減速制動(dòng)段。在勻速接近段追蹤器以某固定速度向目標(biāo)接近，當(dāng)小于某距離時(shí)轉(zhuǎn)入減速制動(dòng)段，開(kāi)啟反向推力發(fā)動(dòng)機(jī)，將追蹤器速度迅速減小，直至滿(mǎn)足對(duì)接要求為止。下面對(duì)兩個(gè)工作段的制導(dǎo)方式分別開(kāi)展設(shè)計(jì)。

2.1 勻速接近段

由式（3）可得比例導(dǎo)引控制加速度為

式中K為有效導(dǎo)引比。當(dāng)K＞2時(shí)，視線(xiàn)角速度與角加速度反號(hào)，可滿(mǎn)足比例導(dǎo)引角速度收斂條件。

式（5）為發(fā)動(dòng)機(jī)推力可任意變化的比例導(dǎo)引控制方程，而實(shí)際情況下軌控發(fā)動(dòng)機(jī)提供的推力是常值，比例導(dǎo)引不能直接使用。需要對(duì)固定推力比例導(dǎo)引進(jìn)行研究。

比例導(dǎo)引的思想在于抑制視線(xiàn)的旋轉(zhuǎn)，如果利用比例導(dǎo)引確定發(fā)動(dòng)機(jī)的開(kāi)啟和關(guān)閉，將交會(huì)過(guò)程中的視線(xiàn)角速率控制在較小的范圍內(nèi)，也可以達(dá)到與比例導(dǎo)引相近的效果。

首先研究利用比例導(dǎo)引確定發(fā)動(dòng)機(jī)開(kāi)啟控制線(xiàn)。將式（5）代入式（3），得到：

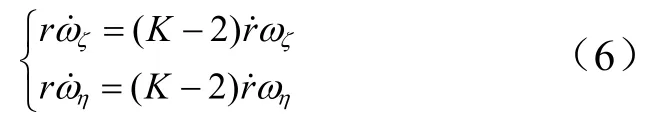
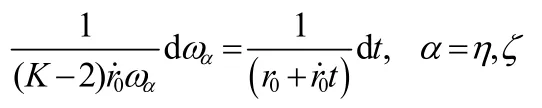
積分得到：

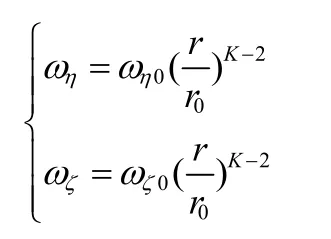
發(fā)動(dòng)機(jī)開(kāi)啟控制線(xiàn)為

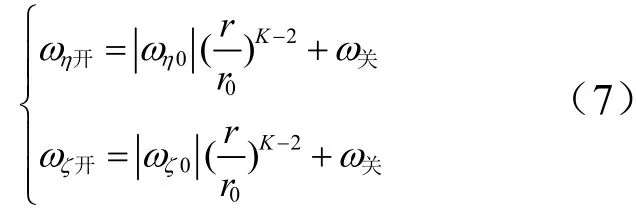
式中ω關(guān)＞0，為發(fā)動(dòng)機(jī)關(guān)閉控制線(xiàn)，可由導(dǎo)引頭測(cè)量靈敏度確定；ωη0和ωζ0為初始視線(xiàn)角速度。可見(jiàn)，K＞2時(shí)，利用上式得到的發(fā)動(dòng)機(jī)開(kāi)啟控制線(xiàn)隨著距離r的減小而持續(xù)收斂，直至與發(fā)動(dòng)機(jī)關(guān)閉控制線(xiàn)一致。K值越大，收斂越快。通過(guò)對(duì)發(fā)動(dòng)機(jī)進(jìn)行開(kāi)關(guān)控制，可將對(duì)應(yīng)的角速度控制在開(kāi)啟控制線(xiàn)和關(guān)閉控制線(xiàn)之間的區(qū)域，達(dá)到抑制視線(xiàn)旋轉(zhuǎn)的目的。K=2是臨界狀態(tài)。當(dāng)K＜2時(shí)，無(wú)法實(shí)現(xiàn)角速度收斂的目的。

上述控制方式存在一個(gè)問(wèn)題，隨著追蹤器和目標(biāo)距離的逐漸縮小，開(kāi)啟控制線(xiàn)和關(guān)閉控制線(xiàn)也將逐漸接近，導(dǎo)致軌控發(fā)動(dòng)機(jī)頻繁開(kāi)關(guān)。為了避免該現(xiàn)象，提出一種調(diào)整開(kāi)啟控制線(xiàn)終值的方法。在保證制導(dǎo)精度的前提下，將開(kāi)啟控制線(xiàn)的收斂終值從ω關(guān)處適當(dāng)增加至ω開(kāi)end，使得ω開(kāi)end＞ω關(guān)。則發(fā)動(dòng)機(jī)開(kāi)啟控制線(xiàn)變?yōu)?/p>

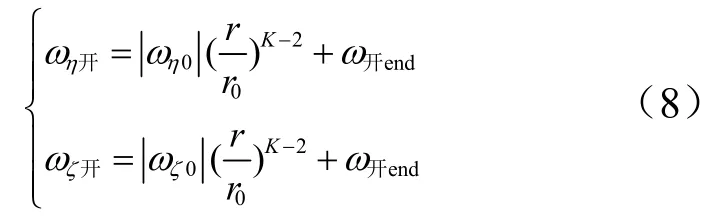
采用非線(xiàn)性開(kāi)關(guān)函數(shù)實(shí)現(xiàn)對(duì)發(fā)動(dòng)機(jī)開(kāi)關(guān)的控制，如圖1所示。

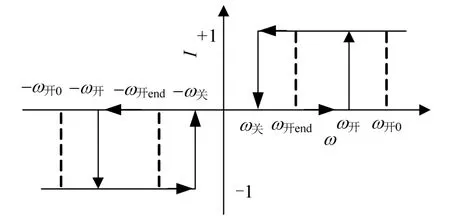
圖1 發(fā)動(dòng)機(jī)非線(xiàn)性開(kāi)關(guān)函數(shù)Fig.1 Nonlinear Switch Function of the Engine

函數(shù)表示方式如下：

I-1表示上一控制周期的發(fā)動(dòng)機(jī)開(kāi)關(guān)指令。使用此控制方式可以將視線(xiàn)角速度控制在(ω關(guān)，ω開(kāi))或(-ω開(kāi)，-ω關(guān))區(qū)間內(nèi)，而ω開(kāi)在交會(huì)過(guò)程中從初值ω開(kāi)0隨著距離縮短逐漸縮小至ω開(kāi)end，實(shí)現(xiàn)了抑制視線(xiàn)旋轉(zhuǎn)的作用。

2.2 減速制動(dòng)段

在減速制動(dòng)段，為滿(mǎn)足對(duì)接要求，追蹤器進(jìn)行減速制動(dòng)，速度逐漸減小至1 m/s以下。由式（3）后兩式可知，由于ηω和ζω在勻速接近段已收斂為小量，則在減速制動(dòng)段存在如下近似公式：

由于控制加速度aη和aζ為常值，由式（9）可知，在進(jìn)入減速制動(dòng)過(guò)程后，速度減小的同時(shí)距離r也將不斷減小，角速度變化率將逐漸變大。控制加速度在一個(gè)控制周期內(nèi)就足以使角速度產(chǎn)生較大變化，導(dǎo)致角速度將突破(ω關(guān)，ω開(kāi))或(-ω開(kāi)，-ω關(guān))的預(yù)期區(qū)間，而在(ω開(kāi)，+∞)和(-∞，-ω開(kāi))兩個(gè)區(qū)間頻繁反復(fù)跳動(dòng)，且隨著r減小呈發(fā)散趨勢(shì)。由于這一階段速度較小，發(fā)散過(guò)程將持續(xù)較長(zhǎng)時(shí)間，這對(duì)末段逼近對(duì)接是很不利的。

為解決上述問(wèn)題，這里提出發(fā)動(dòng)機(jī)開(kāi)啟控制線(xiàn)按照控制加速度確定，并隨速度調(diào)整的方式，由式（5）得到發(fā)動(dòng)機(jī)開(kāi)啟控制線(xiàn)：

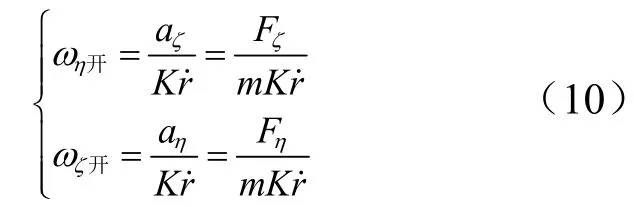
式中Fη，F(xiàn)ζ為對(duì)應(yīng)方向的發(fā)動(dòng)機(jī)推力值；m為追蹤器質(zhì)量，均為已知量。

在進(jìn)入減速制動(dòng)段后，通過(guò)上式控制軌控發(fā)動(dòng)機(jī)的開(kāi)啟，即可保證在角速度偏差達(dá)到控制加速度能力門(mén)限時(shí)再開(kāi)啟發(fā)動(dòng)機(jī)，充分利用控制加速度實(shí)現(xiàn)對(duì)角速度的收斂控制，避免出現(xiàn)發(fā)動(dòng)機(jī)的頻繁開(kāi)啟和角速度的反復(fù)跳動(dòng)，同時(shí)保證交會(huì)精度。

3 仿真分析

為了驗(yàn)證設(shè)計(jì)結(jié)果的有效性，引入瞬時(shí)交會(huì)偏差的概念。瞬時(shí)交會(huì)偏差是指追蹤器和目標(biāo)以當(dāng)前時(shí)刻的狀態(tài)保持勻速飛行，在交會(huì)過(guò)程中，追蹤器與目標(biāo)之間的最小距離[9]。

3.1 勻速接近段仿真分析

分別選擇表1中不同的初始狀態(tài)，針對(duì)表2是否調(diào)整開(kāi)啟控制線(xiàn)收斂終值2種控制方式進(jìn)行仿真分析。仿真參數(shù)ω關(guān)=0.001 （°）/s，4K=，不考慮減速制動(dòng)段，在距目標(biāo)200 m處計(jì)算瞬時(shí)交會(huì)偏差。仿真結(jié)果見(jiàn)表3。

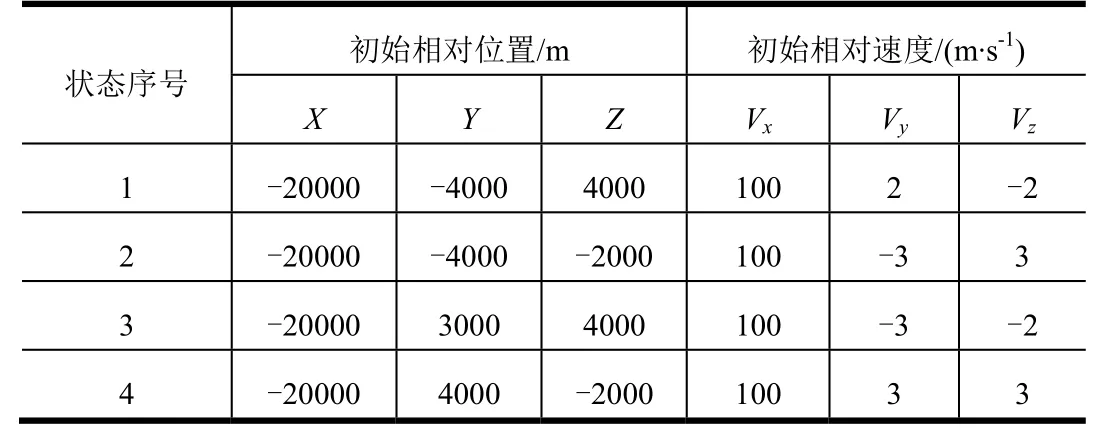
表1 仿真初始狀態(tài)Tab.1 Initial State of Simulation

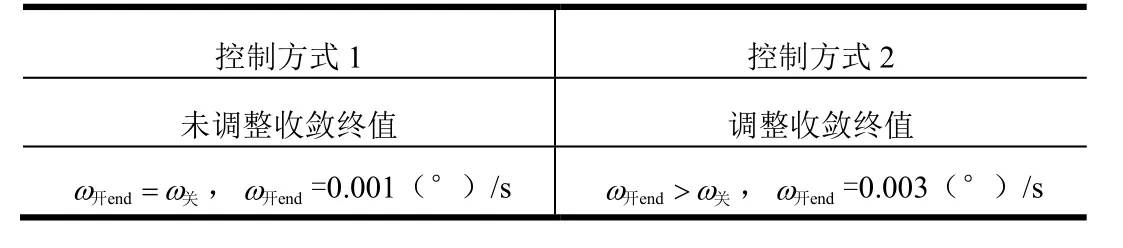
表2 勻速接近段控制方式Tab.2 Control Mode for Uniform Approach Stage

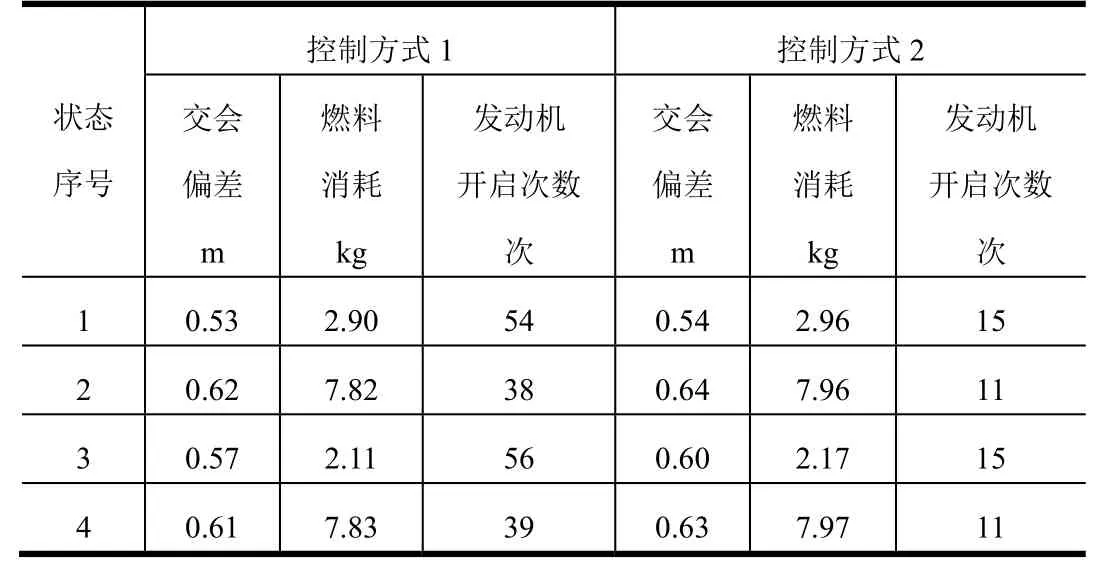
表3 勻速接近段兩種控制方式的仿真結(jié)果比較Tab.3 Comparison of the Simulation Results between Two Control Mode for Uniform Approach Stage

以狀態(tài)1為例，勻速接近段視線(xiàn)角速度和對(duì)應(yīng)的發(fā)動(dòng)機(jī)開(kāi)關(guān)情況如圖2、圖3所示。圖2對(duì)應(yīng)控制方式1，圖3對(duì)應(yīng)控制方式2。從仿真結(jié)果可以看出，兩種方式均實(shí)現(xiàn)了視線(xiàn)角速度的收斂控制，視線(xiàn)角速度控制在(ω關(guān)，ω開(kāi))或(-ω開(kāi)，-ω關(guān))區(qū)間，交會(huì)偏差較小，燃料消耗量基本相當(dāng)。未調(diào)整收斂終值的狀態(tài)，發(fā)動(dòng)機(jī)在勻速接近段后期頻繁開(kāi)啟。調(diào)整收斂終值后，發(fā)動(dòng)機(jī)開(kāi)啟次數(shù)顯著減少。

顯然，調(diào)整收斂終值的控制效果更優(yōu)，后續(xù)仿真分析過(guò)程的勻速接近段均采用此方式進(jìn)行控制。

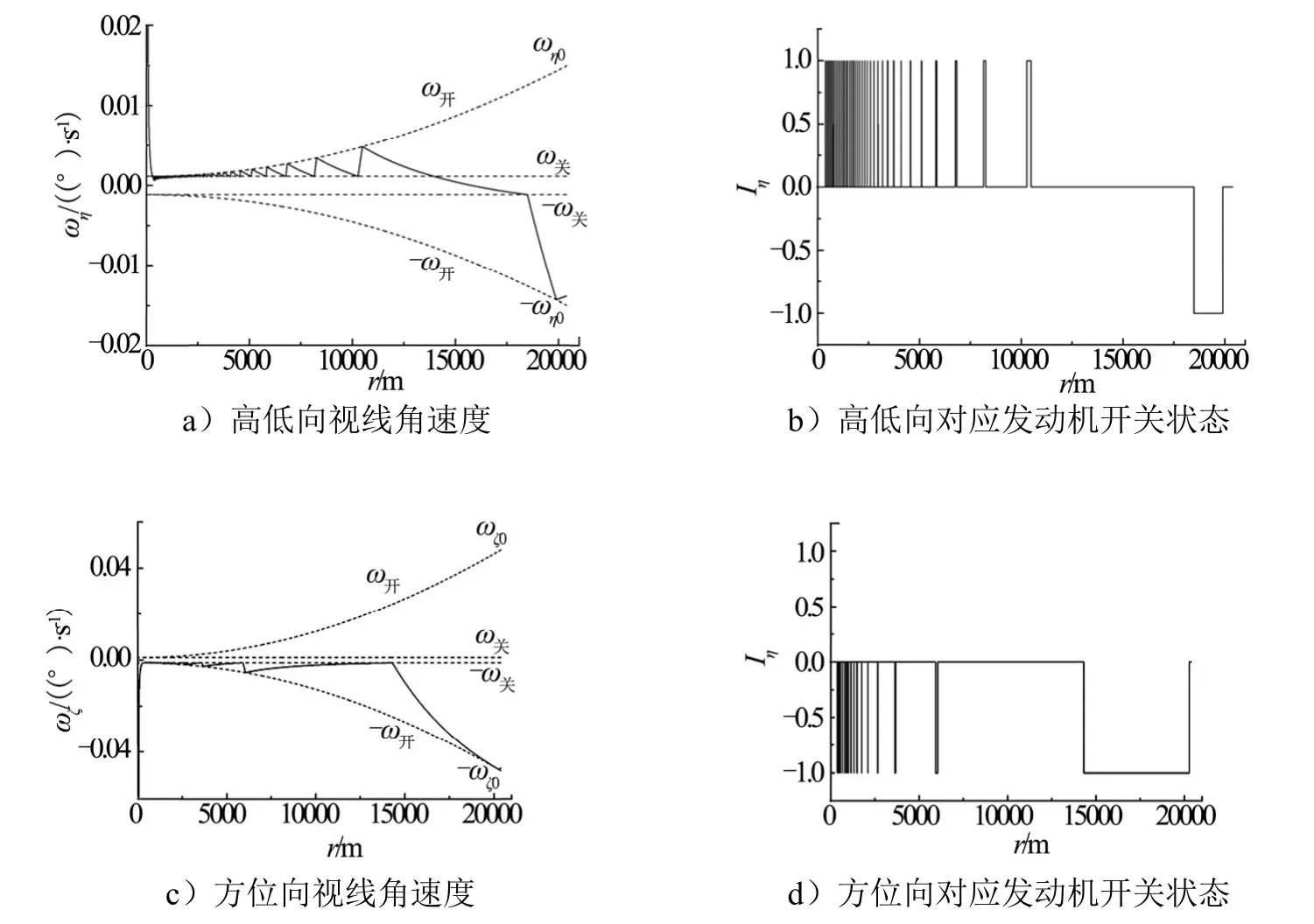
圖2 勻速接近段控制方式1視線(xiàn)角速度和發(fā)動(dòng)機(jī)開(kāi)關(guān)情況Fig.2 Sight Rate and Engine Status of Control Mode 1 for Uniform Approach Stage

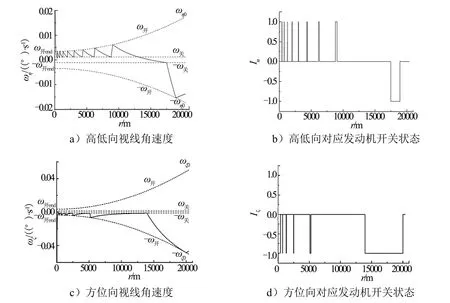
圖3 勻速接近段控制方式2視線(xiàn)角速度和發(fā)動(dòng)機(jī)開(kāi)關(guān)情況Fig.3 Sight Rate and Engine Status of Control Mode 2 for Uniform Approach Stage

3.2 減速制動(dòng)段仿真分析

分別選擇不同的初始狀態(tài)，減速制動(dòng)段按照是否隨速度調(diào)整開(kāi)啟控制線(xiàn)兩種方式進(jìn)行仿真分析（見(jiàn)表4）。在距目標(biāo)200 m處轉(zhuǎn)入減速制動(dòng)段，交會(huì)終端相對(duì)速度為0.5 m/s。仿真結(jié)果見(jiàn)表5。

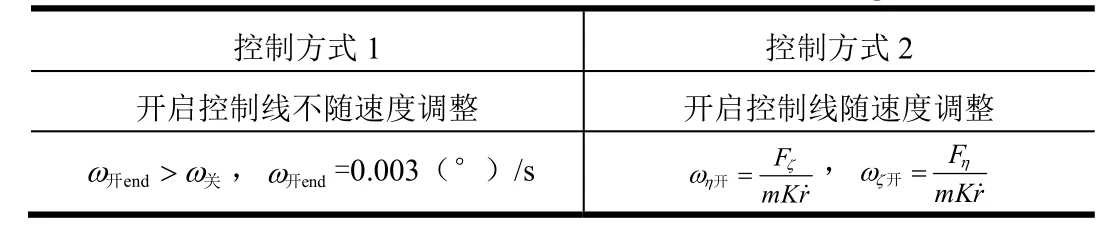
表4 減速制動(dòng)段控制方式Tab.4 Control Mode for Deceleration Stage

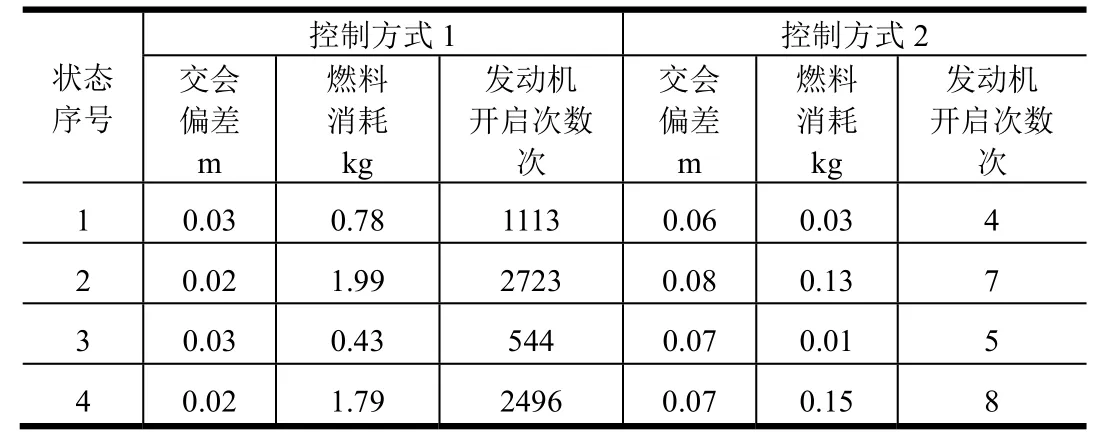
表5 減速制動(dòng)段兩種控制方式的仿真結(jié)果比較Tab.5 Comparison of the Simulation Results between Two Control Mode for Deceleration Stage

以狀態(tài)1為例，減速制動(dòng)段視線(xiàn)角速度和對(duì)應(yīng)的發(fā)動(dòng)機(jī)開(kāi)關(guān)情況如圖4、圖5所示。

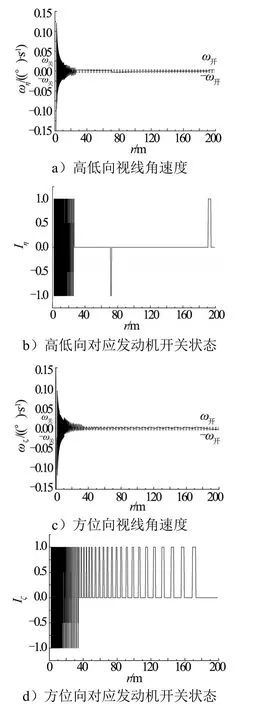
圖4 減速制動(dòng)段控制方式1視線(xiàn)角速度和發(fā)動(dòng)機(jī)開(kāi)關(guān)情況Fig.4 Sight Rate and Engine Status of Control Mode 1 for Deceleration Stage

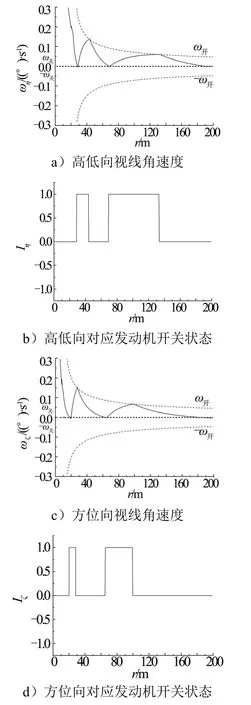
圖5 減速制動(dòng)段控制方式2視線(xiàn)角速度和發(fā)動(dòng)機(jī)開(kāi)關(guān)情況Fig.5 Sight Rate and Engine Status of Control Mode 2 for Deceleration Stage

從仿真結(jié)果可以看出，在減速制動(dòng)段采用與勻速接近段相同的控制方式，將導(dǎo)致軌控發(fā)動(dòng)機(jī)的頻繁開(kāi)啟，角速度隨距離的減小呈發(fā)散趨勢(shì)。改進(jìn)后的制導(dǎo)方式，開(kāi)啟控制線(xiàn)隨速度實(shí)時(shí)調(diào)整，軌控發(fā)動(dòng)機(jī)開(kāi)啟次數(shù)和燃料消耗均顯著減少，交會(huì)精度保持了較高的水平。

3.3 對(duì)機(jī)動(dòng)目標(biāo)的適應(yīng)性仿真分析

上述的分析和仿真過(guò)程中均未考慮目標(biāo)機(jī)動(dòng)，而實(shí)際應(yīng)用中，目標(biāo)是有可能機(jī)動(dòng)的。由比例導(dǎo)引原理和式（5）可知，如果要滿(mǎn)足比例導(dǎo)引收斂條件，追蹤器的控制加速度應(yīng)大于目標(biāo)的機(jī)動(dòng)加速度，且加速度差應(yīng)滿(mǎn)足如下條件。

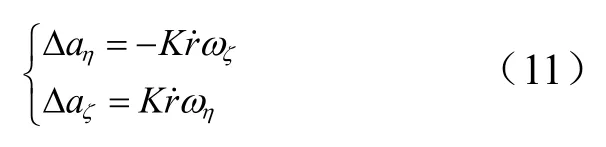
式中aηΔ和aζΔ為視線(xiàn)坐標(biāo)系2個(gè)方向上的加速度差。

本仿真模型中，追蹤器產(chǎn)生的控制加速度為0.3 m/s2，目標(biāo)機(jī)動(dòng)加速度按照最大為0.15 m/s2進(jìn)行仿真。針對(duì)目標(biāo)2種機(jī)動(dòng)形式開(kāi)展仿真分析：a）目標(biāo)做直線(xiàn)加速機(jī)動(dòng)：aTy=aTz=0.15 m/s2；b）目標(biāo)做三角波機(jī)動(dòng)：aTy=aTz=0.15sin(0.1t) m/s2。其它仿真條件同狀態(tài)1。仿真結(jié)果見(jiàn)表6。

表6 對(duì)機(jī)動(dòng)目標(biāo)的適應(yīng)性仿真結(jié)果Tab.6 Adaptability Simulation Results for Maneuverable Target

從仿真結(jié)果可知，本文所提出的制導(dǎo)方式對(duì)機(jī)動(dòng)目標(biāo)的適應(yīng)性較好，仍可以保證較小的交會(huì)偏差。燃料消耗和發(fā)動(dòng)機(jī)開(kāi)啟次數(shù)相對(duì)目標(biāo)無(wú)機(jī)動(dòng)狀態(tài)，存在明顯增加，這是由于跟蹤目標(biāo)過(guò)程中，追蹤器需要根據(jù)目標(biāo)機(jī)動(dòng)狀態(tài)不斷調(diào)整跟蹤方向所致。

4 結(jié) 論

本文對(duì)比例導(dǎo)引應(yīng)用于空間交會(huì)問(wèn)題進(jìn)行了研究，提出一種適應(yīng)固定推力的比例導(dǎo)引律，對(duì)非機(jī)動(dòng)目標(biāo)和機(jī)動(dòng)目標(biāo)均有良好的制導(dǎo)效果。通過(guò)對(duì)發(fā)動(dòng)機(jī)開(kāi)啟控制的優(yōu)化設(shè)計(jì)，在保證較高制導(dǎo)精度的同時(shí)，顯著減少了發(fā)動(dòng)機(jī)開(kāi)啟次數(shù)和燃料消耗。