巧用阿氏圓 妙解一類題
魏東升
(江西省瑞金第一中學 342500)
有時我們會有這樣的感慨,有些我們一直以為很熟悉的事物,隨著對其了解的深入,卻發現它們已經越來越陌生了.比如從小到大陪伴著我們成長的圓,可謂是我們接觸的最多的圖形之一了.但隨著學習的深入,當其以阿氏圓、蒙日圓等隱形圓的身份出現在試題中時,不少人卻陌生了.本文通過運用阿氏圓的一個幾何性質解題的幾個視角,讓大家感受到阿氏圓解題的美妙.
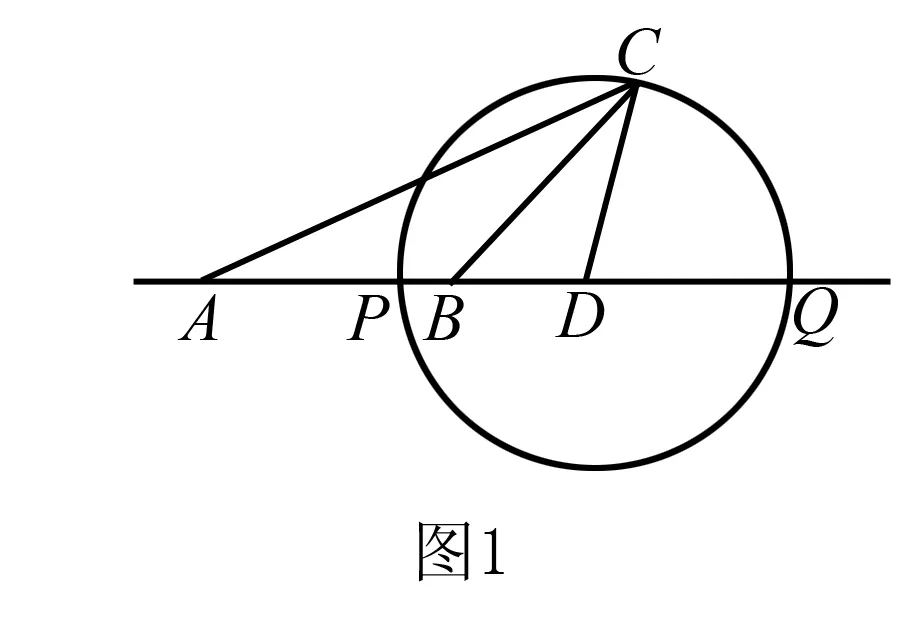
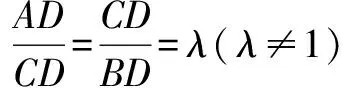
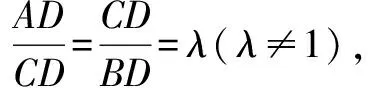
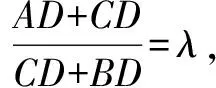
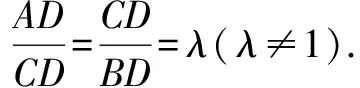
以下例舉該結論妙解相關問題的三個視角:
例1(2019年全國Ⅱ卷理科第15題改編)在△ABC中,角A,B,C的對邊分別為a,b,c.若b=2,a=2c,則S△ABC的最大值為____.
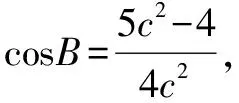
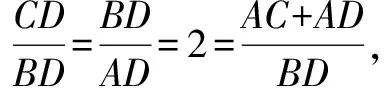
評析本題的通法是運用解三角形的相關知識建立關于面積的函數解析式,其解題思路看似不遜色于妙解,但卻是建立在較大的數學運算量這一基礎上的.
他們雖然分手了,但是許元生還是會在如蕓上晚班的時候,等著她一起下班,跟在她身后,偷偷送她回家。看她上了樓,窗口的燈亮了,他才走。
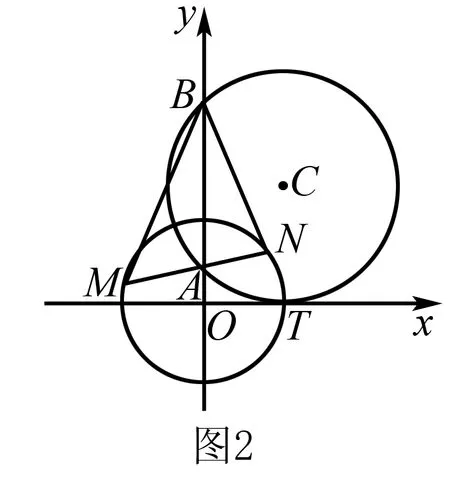
例2 (2015年湖北卷理科第14題)如圖2,圓C與x軸相切于點T(1,0),與y軸正半軸交于兩點A,B(點B在點A的上方),且|AB|=2.
(1)圓C的標準方程為____;
(2)過點A任作一條直線與圓O:x2+y2=1相交于M,N兩點,下列三個結論:
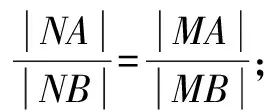
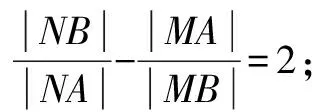
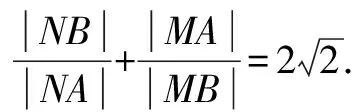
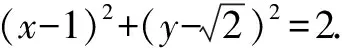
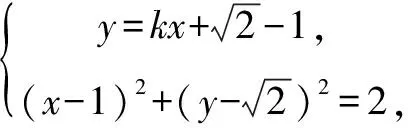
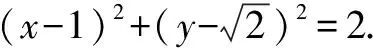
評析此題的妙解可謂是把阿氏圓解題的優勢體現地淋漓盡致!通法實際上是在不知道阿氏圓這一幾何背景下的純代數運算,屬于典型的“小題大做”,這樣處理實在是有點得不償失,雖然是一道填空題的壓軸題!
例3 (江西省贛州市2021年期中聯考理科第15題)已知a,b,c是平面內三個單位向量,a·b=0,則|a+2c|+|2a+b-c|的最小值為____.
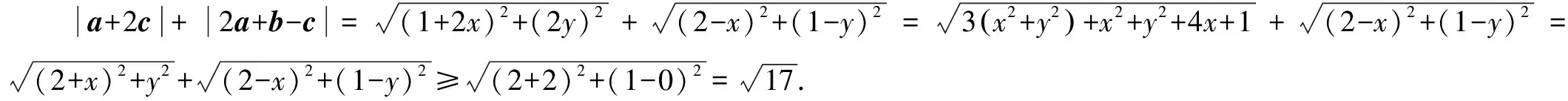
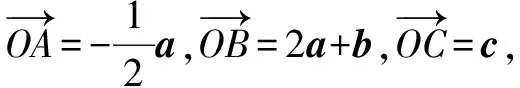
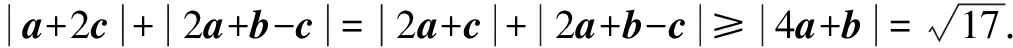
評析通解的思路是向量問題代數化,很好地體現了“向量數與形融為一體”這一顯著特點,但較之基于阿氏圓背景的妙解1運算量偏大.妙解2很好地運用了向量的幾何性質,其解法可謂“大道至簡”,是神來之筆!
本文主要探究了阿氏圓中的一個幾何性質在不同數學知識板塊中的應用,給我們在解決這類問題帶來了啟發.像這樣利用蒙日圓和阿氏圓等知識進行專題教學,對同學們解題素養的提升是很有幫助的.需要指出的是,在專題學習時同學們不可陷入解題的思維定式,應該讓新方法完善和充實我們的解題系統.如在學習中發現阿氏圓好用便只從阿氏圓的角度思考和解決問題,掉入用“新知識”覆蓋“舊知識”的陷阱,以致“邯鄲學步”,其實很多在我們看來不起眼的“舊知識”往往能給我們帶來驚喜,這一點例3的妙解2就做了很好的詮釋.

