現澆箱梁拼寬橋上部結構受力特性分析

沙嵩

（華設設計集團股份有限公司，南京210000）

1 引言

我國對于拼寬橋的研究起步較晚，最早是進行T梁和空心板梁橋的拼寬，在進行拼寬時將新舊橋梁通過濕接縫和橫隔板等進行連接，后期運行過程中會存在沉降等問題。為解決拼寬橋帶來的問題，相關學者進行了研究。徐志強[1]通過有限元分析了T梁橋拼接后上部結構內力變化，通過對橋梁的橫向力分布系數進行計算，表明提高剛度可降低橋梁內部應力。王曦婧[2]通過研究表明，基礎沉降對箱梁的受力影響最大，且發生沉降最不利位置為邊跨和中跨支點。王亞東[3]通過研究橋梁的收縮徐變產生的內力變化，結果表明，半剛性連接結構的拉應力較小，剛性連接橋梁的穩定性能良好。通過以上內容研究使我國的拼寬橋梁得到了較快的發展，但該類問題仍然存在不足，因此，文章研究內容具有一定的指導意義。

2 上部結構受力影響因素

2.1 拼寬橋與原橋的不均勻沉降

橋梁在后期運營過程中產生不均勻沉降是不可避免的。新舊橋梁在建造時間上存在一定的差異，因此，在運營過程中會出現不均勻沉降，不均勻沉降也是導致新舊橋梁不能協調變形的主要因素。拼寬的T梁橋受到沉降差的影響，會使內力增大，從而發生病害，最危險的結構為T梁橫隔板。因此在橋梁進行施工時，應采取必要措施降低橋梁基礎的沉降量，如采用樁基礎、增大樁長和樁徑，施工前對地基進行處理，如強夯、換填基礎等。

2.2 混凝土的收縮徐變

混凝土由于自身特性，在澆筑完成后會存在收縮徐變，新舊橋由于建橋時間不一致，在連接部位處存在齡期差，舊橋混凝土的收縮徐變比新橋的收縮徐變快，該現象會導致拼寬箱梁連接部位受力發生改變（附加應力增大）。因此，在進行箱梁拼接時要著重對新舊橋混凝土的齡期差進行分析。

3 偏載系數計算分析

3.1 工程概況

本文所依據的項目為某地區的拼寬橋，橋梁全長162 m，橋梁縱向布置為48.5 m+72 m+41.5 m，拼寬后橋梁全寬為57.5 m，設計速度為40 km/h，人群荷載取值為2.9 kN/m2，原橋結構與新橋結構采用相同形式，均為單箱雙室。

新橋縱向布置為48.5 m+72 m+41.5 m，結構形式為單箱單室的連續箱梁，截面參數詳見表1。

表1 新橋箱梁截面參數表m

3.2 橋梁模型建立

本文的橋梁模型通過Midas Civil建立，對橋梁模型的節點進行驗算，對截面的各個參數進行修正，梁格模型建立如圖1所示。

圖1 橋梁模型圖

3.3 偏載系數分析

應力增大系數的定義為：在偏載作用下，截面出現的最大應力值與平均應力值的比。類比推理的方式可以得到撓度增大系數的定義。通過應力增大系數與撓度增大系數之間的數量關系得到橋梁的偏載系數。橋梁控制截面如圖2所示。

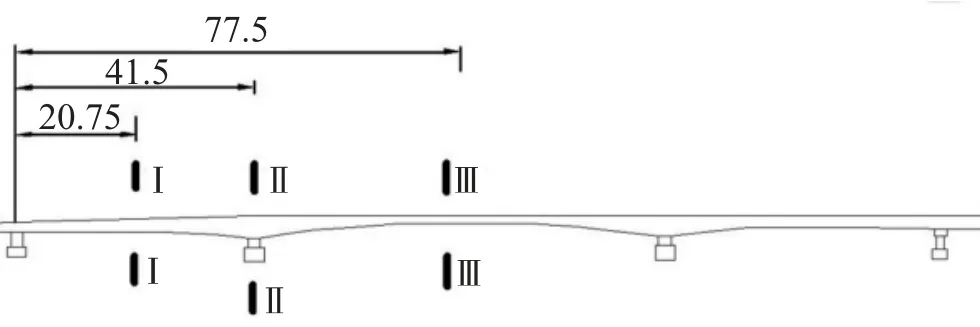
圖2 橋梁控制截面圖（單位：m）

1）通過建模分析計算可以得到新橋在拼接前截面Ⅰ-Ⅰ和Ⅲ-Ⅲ的撓度偏載系數分別為1.11和1.0；進行鉸接后截面Ⅰ-Ⅰ和Ⅲ-Ⅲ的偏載系數為1.05和1.03；進行剛接后截面Ⅰ-Ⅰ和Ⅲ-Ⅲ的偏載系數為1.05和1.02。

由于截面Ⅱ-Ⅱ是支座截面，所以忽略撓度偏載系數的影響。由計算結果可知，無論是鉸接還是剛接，橋梁的剛度均有不同程度提高，橋梁的偏載系數也有所降低，這樣可以節約資源的消耗。本節撓度偏載系數取值為1.12。

2）通過建模分析計算可以得到新橋在拼接前截面Ⅰ-Ⅰ、Ⅱ-Ⅱ和Ⅲ-Ⅲ的應力偏載系數分別為1.15、1.15和1.13；進行鉸接后截面Ⅰ-Ⅰ、Ⅱ-Ⅱ和Ⅲ-Ⅲ的應力偏載系數分別為1.1、1.12和1.04；進行剛接后截面Ⅰ-Ⅰ、Ⅱ-Ⅱ和Ⅲ-Ⅲ的應力偏載系數分別為1.09、1.12和1.03。

由計算結果可得，無論是鉸接還是剛接，橋梁的剛度均有不同程度提高，橋梁的應力有所降低，偏載系數也隨著降低。為滿足結構承載力的要求，應力偏載系數取值為1.15。

4 混凝土收縮徐變對拼接箱梁的影響

本文通過建立模型來對混凝土的收縮徐變進行分析，模型在建立過程中主要考慮因素有：新橋建成后與原橋進行剛性拼接，收縮徐變過程中考慮混凝土和鋼筋等材料的自重，條件假定為原橋無收縮徐變，新橋混凝土產生收縮徐變，分析該過程中產生的內力變化。

4.1 混凝土收縮的影響

通過有限元對模型進行分析可知，不同齡期混凝土收縮引起的應力類型主要有：軸力、橫向剪力及橫向彎矩，其余應力變化值較小，可以忽略不計。因此，該節主要對軸力、橫向剪力及橫向彎矩進行相應分析。

4.1.1 軸力分布

在混凝土收縮差的作用下，拼寬橋梁上部結構的軸力以跨中為軸線對稱分布，新橋在主梁位置的軸力表現為拉力，在沿橋方向上軸力分布為中跨軸力大于邊跨軸力。每跨的軸力值大小相等。新橋在橫橋方向內外邊梁的軸力差值較小。混凝土收縮差在原橋的軸力形式表現為壓力，在沿橋方向上軸力分布為中跨軸力大于邊跨軸力，新橋在橫橋方向內外邊梁的軸力分布為：外邊梁向內邊梁逐漸遞增。通過變化規律可知：混凝土發生收縮時，原橋主要產生軸力。

4.1.2 橫向剪力分布

新舊橋梁的混凝土收縮存在差值，新橋主梁剪力最大值位于中墩支座的兩端，該值大小相當，方向相反。在每一跨內主梁的剪力分布情況近乎相同，變化規律為沿橋方向先減小后反向增大。新橋和原橋在橫橋方向的剪力分布規律相同，均為內邊梁的剪力大于外邊梁的，因此，新舊橋梁混凝土收縮差的橫向剪力由內外邊梁共同承擔。

4.1.3 橫向彎矩分布

新舊橋梁的混凝土收縮存在差值，新橋縱橋方向的最大彎矩位于中墩支座的兩端，在每一跨內主梁的剪力分布情況近乎相同，變化規律為沿橋方向先減小后反向增大。主梁在支座附近上部受拉，跨中位置處下部受拉。新橋與原橋橫橋方向接縫附近的彎矩分布為內邊梁大于外邊梁。

4.2 混凝土徐變的影響

通過有限元對模型進行分析可知，不同齡期混凝土徐變引起的應力類型主要有：軸力，豎向剪力及彎矩，其余應力變化值較小，可以忽略不計。因此，該節主要對軸力和豎向剪力及彎矩進行相應分析。

4.2.1 軸力分布

在混凝土徐變的作用下，拼寬橋梁上部結構的軸力以跨中為軸線對稱分布，新橋在主梁位置的軸力表現為壓力，在沿橋方向上軸力分布為中跨軸力小于邊跨軸力。每跨的軸力值大小相等。新橋在橫橋方向內外邊梁的軸力差值較小。混凝土徐變差在原橋的軸力形式表現為壓力，在沿橋方向上軸力分布為中跨軸力大于邊跨軸力，新橋在橫橋方向內外邊梁的軸力分布為：外邊梁向內邊梁逐漸遞增。通過變化規律可知：混凝土發生徐變時，原橋主要產生軸力。

4.2.2 豎向剪力分布

新舊橋梁的混凝土徐變存在差值，新橋主梁剪力最大值位于中墩支座的兩端，該值大小相當，方向相反。在每一跨內主梁的剪力分布情況近乎相同，變化規律為沿橋方向先減小后反向增大。新橋和原橋在橫橋方向的剪力分布規律相同，均為內邊梁大于外邊梁，但剪力分布方向相反。因此，新舊橋梁混凝土徐變差的豎向剪力由內邊梁承擔。

4.2.3 豎向彎矩分布

新舊橋之間存在徐變差異，新橋在順橋方向的彎矩最大值位于中墩支座兩端，每一跨內彎矩變化為支座向跨中逐漸遞減，然后反向增大，主梁跨中位置上部受拉。新橋在橫橋方向主梁彎矩變化為：外邊梁小于內邊梁。原橋主梁順橋向的彎矩變化規律與新橋相似，但方向相反。橫橋向彎矩由外邊梁向內邊梁逐漸增加。

5 結語

本文通過對箱梁拼寬橋上部結構進行分析得到以下結論：

1）箱梁拼寬橋上部結構的受力主要是由于原橋與新建橋梁基礎的不均勻沉降以及混凝土自身的收縮徐變引起的。

2）通過對拼寬橋梁進行建模分析可知在設計時拼寬橋的撓度偏載系數取值可取1.12，應力偏載系數取值可取1.15，此時達到節省資源，滿足承載力要求的特性。

3）混凝土收縮會引起附加應力，該應力主要發生方向為橫橋向，使橋梁產生軸力、橫向剪力及彎矩。軸力分布形式為跨中對稱分布，最大值出現在中跨跨中位置。

4）混凝土徐變會引起附加應力，該應力主要發生方向為豎橋向，使橋梁產生軸力、豎向剪力及彎矩。軸力分布形式為跨中對稱分布。豎向剪力及彎矩最大值位于中墩支座。