基于相關支持矩陣機的滾動軸承故障診斷方法研究*

陳 英,陳木榮

(1.長沙民政職業技術學院 電子信息工程學院,湖南 長沙 410004;2.華南理工大學 機械與汽車工程學院,廣東 廣州 510640;3.廣東理工學院 機電工程系,廣東 肇慶 526100)

0 引 言

滾動軸承是旋轉機械設備中必不可少的重要零件,其狀態的好壞直接影響整個機械設備的安全運行。因此,對滾動軸承工作狀態的監測及其故障識別一直是學者們的研究熱點。

隨著對滾動軸承狀態判別算法研究的不斷深入,各種故障識別器被應用于滾動軸承故障識別領域,并取得了一定的效果[1,2]。

隨著模式識別算法的快速發展,各種分類器(算法)被廣泛應用于滾動軸承狀態識別中,如支持向量機(support vector machine,SVM)、線性判別分析、k近鄰、貝葉斯分類器、極限學習機(extreme learning machine,ELM)等[3-8]。

上述經典分類器是在輸入特征為向量形式的基礎上構造的。而在實際應用中,拾取的滾動軸承振動信號記錄了一段時間內的波動信息,使其以二維矩陣的形式得以表現出來。為適應傳統分類器對輸入數據的形式要求,通常需要將拾取的特征矩陣重塑為向量,或以向量形式提取特征。然而,由于二維振動信號行和列之間的高度相關性,矢量化會破壞特征矩陣的列或行之間的結構信息[9]。

為了解決上述問題,LUO Luo等人[10]提出了一種新的支持矩陣機(support matrix machine,SMM),它可以充分利用特征矩陣的結構信息,采用交替方向乘子法,來優化SMM的目標函數,獲得良好的分類效果。

此外,在SMM的基礎上,相關學者又陸續提出了一系列的改進算法。ZHENG Qing-qing等人[11,12]提出了多分類支持矩陣機(multiclass support matrix machine,MSMM)和稀疏支持矩陣機(sparse support matrix machine,SSMM);PAN Hai-yang等人[13]提出了辛增量矩陣機(symplectic incremental matrix machine,SIMM);YE Yun-fei等人[14]提出了多距離支持矩陣機(multi-distance support matrix machines,MDSMM);LI Xin等人[15]提出了辛加權稀疏支持矩陣機(symplectic weighted sparse support matrix machine,SWSSMM)。

SMM及其改進算法都是以矩陣形式對滾動軸承的含噪信號、冗余特征等進行分類,可以完成不同工況下的分類問題。

隨著SMM算法的理論和應用研究的不斷增加,該方法的一些不足之處也逐漸顯現出來,如結果缺乏必要的概率信息,預測的結果不具有統計意義,預測結果的不確定性無法估算,等。同時,隨訓練樣本集的規模增大,采用該方法所獲得的支持向量的個數也呈線性增長,這使得模型的稀疏性有限[16]。

鑒于SMM的不足,筆者結合再生核希爾伯特空間(reproducing kernel Hilbert space,RHKS)[17],并利用貝葉斯統計方法進行推理,提出了一種相關支持矩陣機(relevance support matrix machine,RSMM)。

與SMM方法相比,RSMM是一種基于貝葉斯框架的統計學習方法,該方法利用貝葉斯學習框架,為模型參數施加一個條件概率分布的約束,可以得到稀疏的解空間。同時,在SMM方法中,只有滿足Mercer條件限制的核函數,才可以用來構造非線性的SMM。由于RSMM是以貝葉斯統計框架構造的模型,其核函數不受Mercer條件限制,可以獲得各類別之間的概率統計信息,從而可以對不確定樣本進行分類。

此外,多核函數的引入可以解決由多個不同數據源帶來的復雜問題;將先驗概率引入到模型權重設置中,利用超參數對權重進行一對一分配,可使多數權值的后驗分布近似于零。由此可以說明,RSMM模型是稀疏的,且在復雜數據模式識別中,在特征提取的多元化和異常數據的多樣性方面,該方法具有較好的適用性。

綜上所述,筆者在矩陣多元化和貝葉斯框架的基礎上,提出一種RSMM算法,來獲得各類別之間的概率統計信息,進而對不確定樣本進行分類;最后,進行滾動軸承故障分類實驗,采用滾動軸承數據集對該方法的性能進行檢驗。

1 相關支持矩陣機

樣本數據集為:

ZC={Zi,yj|Zi∈RS×N}

(1)

式中：C—類別數;S—樣本數;N—每個樣本的長度。

其中:i=1,2,…,N;j=1,2,…,C。

針對式(1),引入初始輔助變量Y∈RS×C和權矩陣W∈RS×C,筆者構造標準噪音回歸模型如下:

ysc|wc,ks～Nysc(kswc,1)

(2)

式中:ysc—Y的第s行c列的元素;wc—W的第c列;Nysc(kswc,1)—ysc服從均值為kswc,方差為1的正態分布;ks—特征集數。

ZC核函數K的行也代表訓練集中第s個樣本數據與其他樣本數據的相似度。引入多項概率鏈接函數,可以將回歸目標轉化為類別標簽,即:

ts=i,ysi>ysj(i≠j)

(3)

因此,根據多項概率似然函數原理,其分類表達式可以表示為:

(4)

式中:u—服從N(0,1)分布;Φ—高斯累積分布函數。

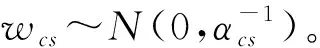
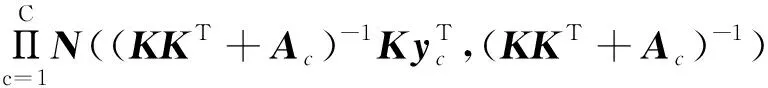
(5)

式中:Ac—由A的c列對應的對角矩陣。

由log邊緣似然函數可以推導出:

(6)

式中:C=I+QA-1QT。

C可以分解為:

(7)

式中:C-i—刪除第i個樣本后的C值。由此可以得出:

(8)

Log邊緣似然函數可被分解為:

L(α)=L(α-i)+l(αi)

(9)

式中：ei—稀疏因子;gci—量化因子。

通過求解?L(A)/?αi=0,可得駐點αi。

在模型訓練過程中,由最大后驗概率估計的方法可得:

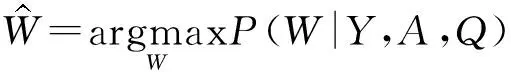
(10)

因此,給定類別時,基于最大后驗概率的權重更新方法為:

(11)

根據上式,對于第i類,其輔助變量表達式為:

(12)

先驗參數的后驗概率分布的表達式為:

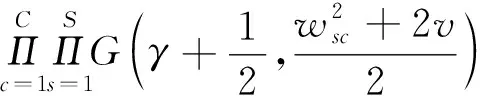
(13)

通過更新和訓練,模型參數W的大部分值為0,因此,模型在樣本空間和特征空間上均是稀疏的。對于新的樣本Znew,利用后驗概率式(4)可得:

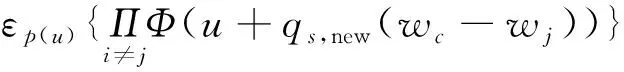
(14)

式(14)即為新樣本屬于類別c的概率。而最大概率對應的類別即為新樣本所屬的類別,即:

(15)

2 基于RSMM的診斷方法

為了驗證RSMM方法在滾動軸承故障診斷上的有效性,筆者將利用美國凱斯西儲大學的滾動軸承數據和湖南大學的滾動軸承試驗數據來進行分析與驗證。

首先,將利用美國凱斯西儲大學數據(故障分類常用數據集)的7種狀態,來證明RSMM在識別率、分類效率和小樣本等方面與其他方法相比有更好的分類性能;

其次,將利用湖南大學的試驗數據(實驗數據具有6種狀態類型),來進一步驗證RSMM的普適性;

最后,為了驗證RSMM方法的優越性,選擇MSMM、SSMM和SIMM進行對比分析。

由于RSMM、MSMM、SSMM和SIMM等方法的輸入元素為矩陣,需要構造輸入矩陣來完成分類和建模。多重同步壓縮變換(multi-synchro squeezing transform,MSST)作為一種新的信號分析方法,已被證明具有良好的特征提取能力。因此,在此處筆者采用MSST來分析原始信號,以獲得可以保存完整結構信息的特征矩陣。

實驗的具體步驟如下:

(1)將不同狀態(一維時間序列)的樣本進行MSST分析,對得到的時頻譜進行灰度化和下采樣,獲得輸入特征矩陣;

(2)將訓練樣本特征矩陣輸入到主程序(MATLAB)中,得到決策函數式(15);

(3)將測試樣本輸入決策函數,得到預測結果;

(4)對各模型的預測結果進行分析,得到各模型的輸出識別狀態。

3 實驗及結果分析

3.1 凱斯西儲大學數據驗證

為了驗證所提方法的有效性,筆者首先利用美國凱斯西儲大學滾動軸承數據進行測試。實驗選擇的滾動軸承型號為SKF6205。

軸承故障模擬試驗臺如圖1所示[18]。

圖1 滾動軸承故障模擬試驗臺

為了模擬滾動軸承的各種故障狀態,筆者采用電火花加工技術,分別在滾動軸承的內圈、外圈和滾動體上加工出裂紋。

實驗中,采樣頻率設置為48 000 Hz,電機轉速設置為1 730 r/min,負載為2.24 kW。筆者在每種狀態下(正常、內圈故障、外圈故障、滾動體故障,故障寬度0.457 2 mm)各采集200個樣本(每個樣本2 048點)。

實驗環境詳細設置如表1所示。

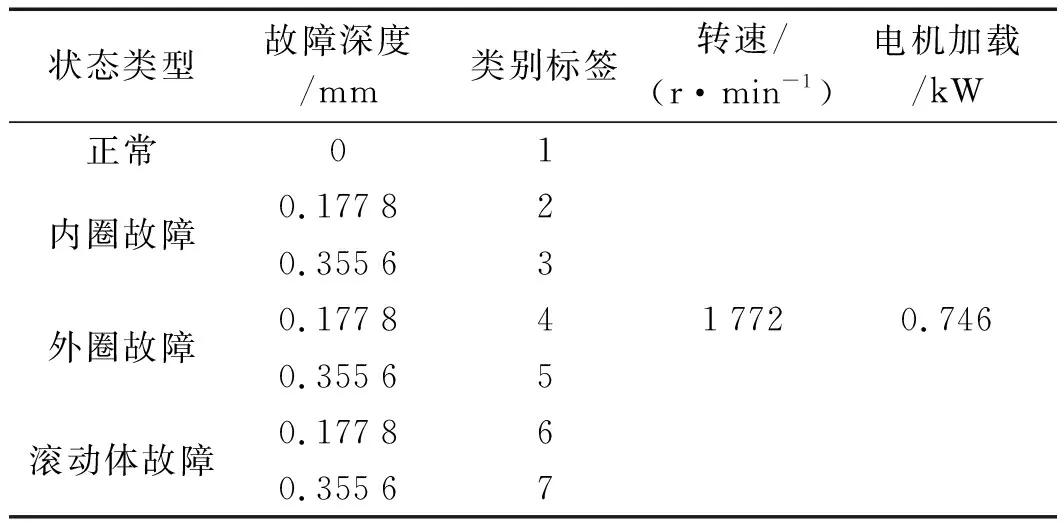
表1 實驗環境設置

筆者隨機抽取100個樣本進行訓練,100組作為測試樣本。

筆者采用MSMM、SSMM、SIMM和RSMM方法分別對滾動軸承實驗數據進行訓練和測試。4種方法識別結果的混淆矩陣如圖2所示。

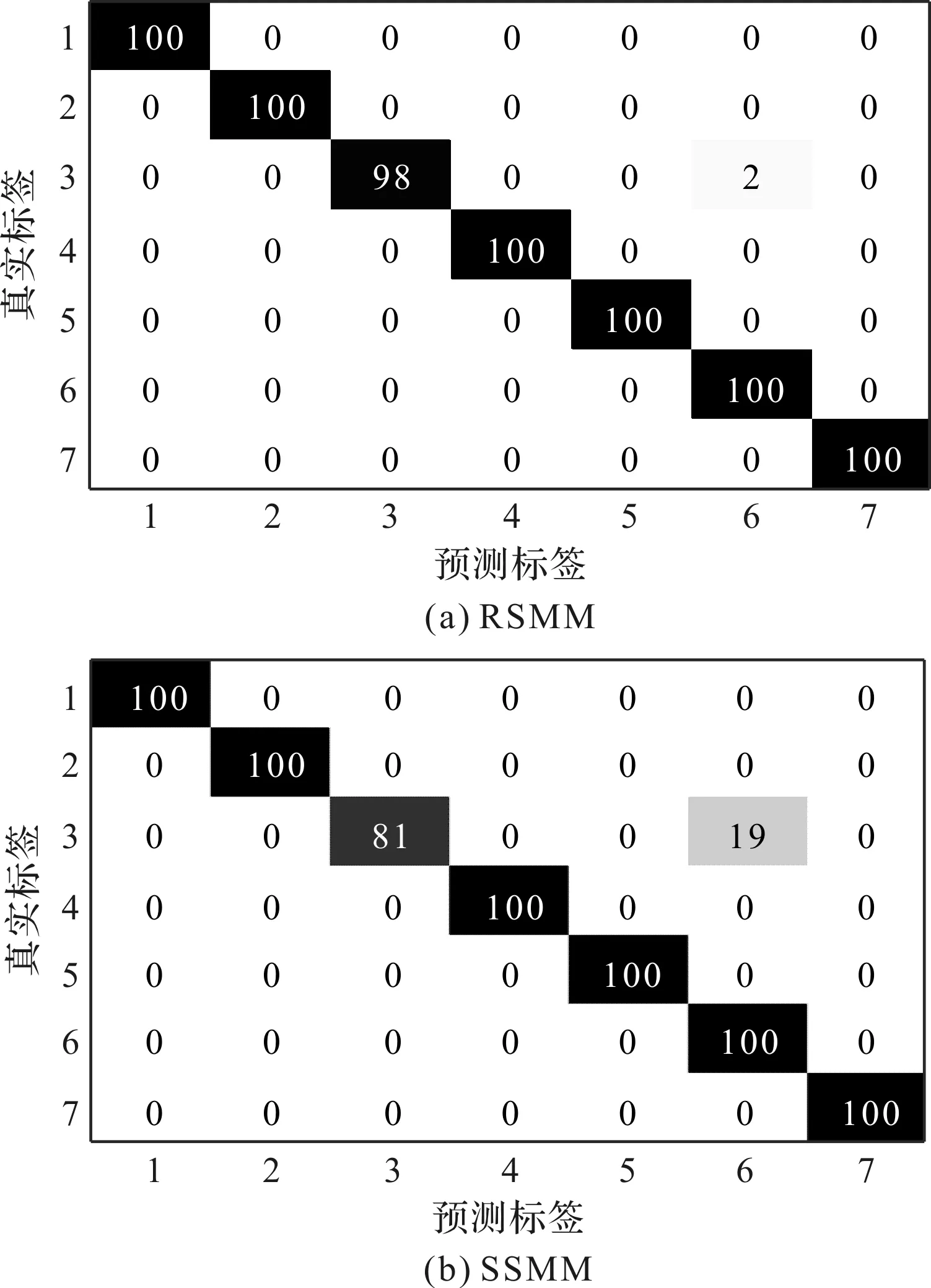
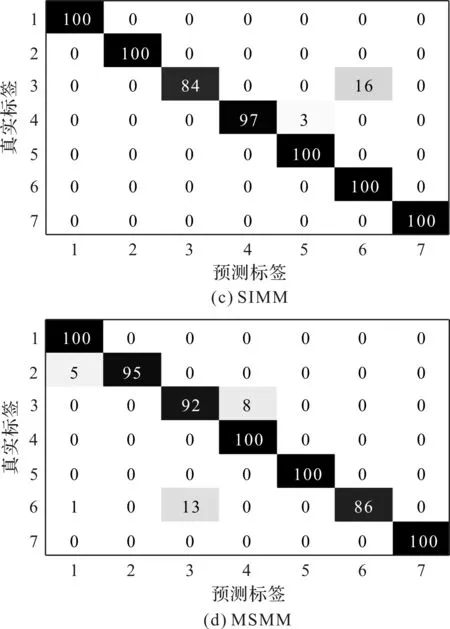
圖2 4種方法識別結果的混淆矩陣1，…，7—滾動軸承狀態類別標簽;橫坐標—訓練樣本的預測標簽;縱坐標—訓練樣本的真實標簽

從圖2可以看出:(1)在所有方法中,采用MSMM的故障診斷效果最差,這是由于MSMM對數據的要求較高,數據復雜度和數據長度會導致MSMM難以收斂;(2)與MSMM相比,SSMM和SIMM在魯棒性和冗余性方面具有一定的優勢,可以得到更好的分類結果。

但是上述方法的結果缺乏必要的概率信息,預測的結果不具有統計意義,預測結果的不確定性無法估算;同時,該方法獲得支持向量的個數基本上隨訓練樣本集的規模呈線性增長,模型的稀疏性有限。

與MSMM、SSMM和SIMM相比,RSMM方法采用核函數獲得信號的傳輸特性,并利用概率框架和先驗概率來確定最可能的狀態類別。因此,RSMM方法具有更優越的性能。

為了進一步驗證RSMM方法分類的客觀性,筆者進行5次隨機分類實驗,即在每個實驗中,隨機抽取100組樣本進行訓練,100組作為測試樣本。

4種方法的識別結果如圖3所示。

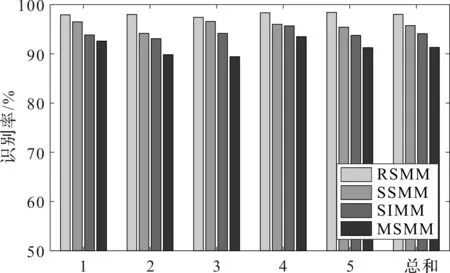
圖3 4種分類方法的分類結果1—5—第1—5次隨機分類實驗

從圖3可以看出:在5次隨機分類實驗中,RSMM的分類效果最好,RSMM方法具有優越的分類性能。

全面評價一種分類方法的分類性能,需要從多個角度進行驗證。因此,筆者選取查準率、召回率、F-score、kappa、準確率等指標進行再次驗證。在一定范圍內,以上5種指標值越大,說明模型的分類性能越好。

各項指標說明如下:

(1)Accuracy為正確率,作為最常用的分類指標,表示分類正確樣本在總體樣本中所占比例;(2)Recall表示召回率,表示在所有正確分類樣本中,正類樣本所占比例;(3)Precision表示精確率,表示真正能被模型識別出來的屬于正類的樣本占比;(4)F1-score為精確率和召回率的調和值;(5)kappa系數常用于一致性檢驗。

同樣,筆者為了克服偶然因素,進行了5次隨機實驗,實驗結果如表2所示。

表2 4種方法分類性能比較(平均值±標準)

從表2可以看出:在各個指標上,RSMM方法都優于其他分類方法,表現出了優越的分類性能。這是因為RSMM方法在貝葉斯框架下進行學習,其核函數不受Mercer條件限制,能夠直接完成多分類問題,且不同核函數的引入有效地解決了不同數據源的數據復雜性問題,提高了算法的分類精度;而SSMM、SIMM、MSMM方法在分類較多、數據較復雜的情況下,分類能力不足。

除了識別率外,分類效率也是評價機器學習方法的一個重要指標。

筆者隨機抽取100個樣本作為訓練樣本,其余100個樣本作為測試樣本。從原始信號的輸入到分類結果的輸出,記錄整個分類過程所消耗的時間。

4種分類方法的分類效率如表3所示。

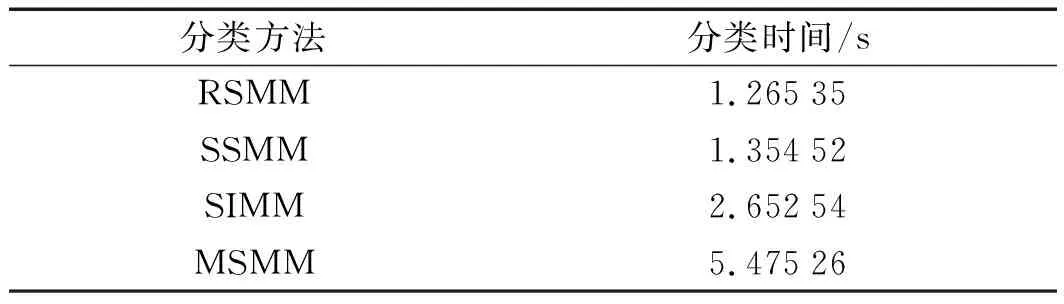
表3 4種分類方法的分類效率對比

由表4可知,利用美國凱斯西儲大學滾動軸承數據集,驗證了RSMM方法的優越性。

3.2 湖南大學數據驗證

為了進一步說明RSMM方法的普適性,筆者再次選擇湖南大學滾動軸承數據集進行驗證[19]。

該滾動軸承故障模擬試驗臺如圖4所示。

圖4 滾動軸承故障模擬試驗臺

實驗環境設置如表4所示。

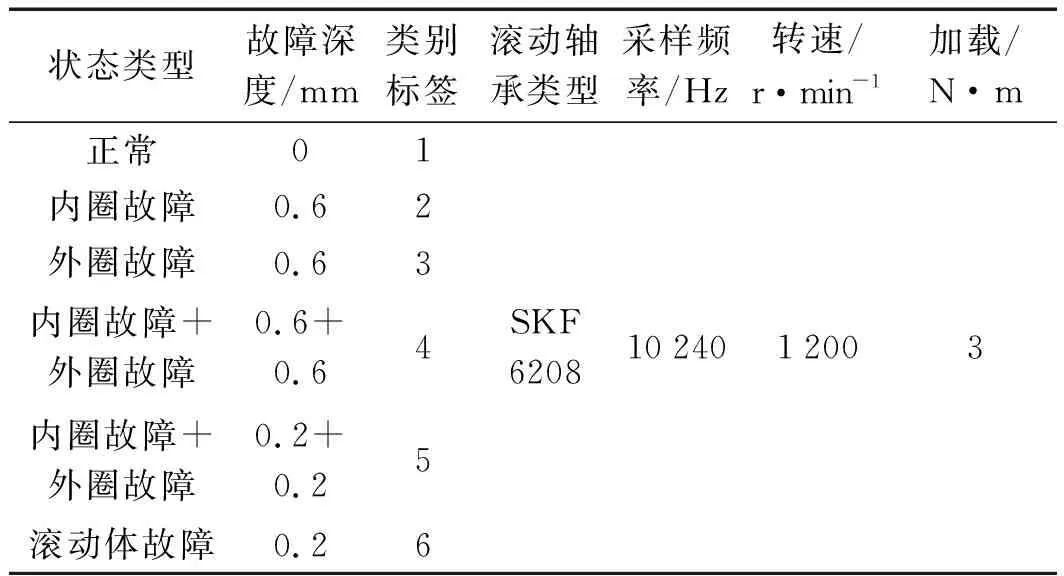
表4 實驗環境設置

在實驗過程中,筆者隨機抽取100組樣本(每個樣本1 024個點)進行訓練,100組作為測試樣本。

4種方法的分類識別結果如圖5所示。

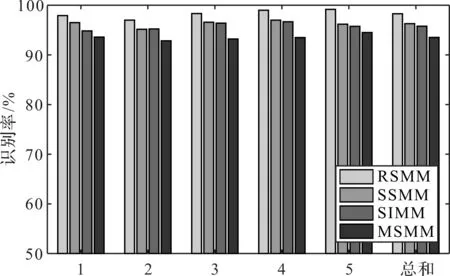
圖5 4種分類方法的分類結果

從圖5可以看出:在5次隨機實驗中,RSMM的分類效果仍然最好。該結果進一步證明了筆者所提出的方法的優越性。

為了全面評價該方法的分類性能,筆者仍然選取查準率、召回率、F-score、Kappa、準確率等指標,同時選擇SSMM、SIMM、MSMM 3種分類方法進行對比分析,以驗證RSMM方法在5種指標下的優越性能。

為了克服偶然因素,筆者獨立進行5次隨機實驗。

4種方法分類性能比較的實驗結果如表5所示。

表5 4種方法分類性能比較(平均值±標準)

綜上所述,根據Accuracy、Recall、Precision、F-score和Kappa等衡量指標下的對比結果可知,在以上4種方法中,RSMM方法的識別結果明顯要優于SSMM、SIMM和MSMM方法。

分析原因可知:

(1)RSMM是一種基于貝葉斯框架的統計學習方法,該方法在貝葉斯框架下進行模型訓練,其核函數不受Mercer條件限制,可以獲得各類別之間的概率統計信息,進而可以對不確定樣本進行分類;

(2)MSMM是一種平行超平面分類器,當輸入數據包含多種復雜特征信息時,數據的復雜性和數據的長度會導致MSMM難以收斂;

(3)采用SSMM和SIMM構建模型的前提是回歸矩陣具有低秩特性,在面對大多數矩陣是多秩的情況下,SSMM和SIMM方法很難發揮其模型本身的優勢。

相比SSMM、SIMM和MSMM方法,RSMM方法是借助于貝葉斯框架思想構造出來的概率統計模型,因此,在采用該方法對不確定樣本(尤其是復雜數據問題)進行分類時,RSMM具有明顯的優勢。

4 結束語

為了解決采用支持矩陣機(SMM)進行分類建模時,缺乏必要的概率信息,而導致其產生的稀疏性和魯棒性不明確的問題,筆者以貝葉斯理論框架為基礎,提出了一種相關支持矩陣機(RSMM),來獲得各類別之間的概率統計信息,進而對不確定樣本進行了分類;最后,進行了滾動軸承故障分類實驗,采用滾動軸承數據集對該方法的性能進行了檢驗。

研究結論如下:

(1)RSMM以樣本信號矩陣作為分類器的輸入,在建模中引入概率框架和先驗概率,使預測結果具有必要的概率信息,并且使預測結果具有統計意義;

(2)在貝葉斯框架下,采用RSMM方法進行模型訓練,其核函數不受Mercer條件的限制,可以獲得各類別之間的概率統計信息,進而可以對不確定樣本進行分類;

(3)滾動軸承故障分類實驗證明,在在Accuracy、Recall、Precision、F-score和Kappa等各項衡量指標方面,RSMM方法均表現出其良好的性能。

由于RSMM方法在滾動軸承故障診斷方面具有良好的表現,可以將其推廣到其他旋轉機械的故障診斷中。然而,RSMM方法仍然存在一些需要改進的地方,如特征冗余性等。

因此,在今后的工作中,筆者所在課題組將對建模過程中的特征冗余性問題進行研究,以進一步提高該算法的識別精度。