基于變模式提取與去趨勢波動分析的液壓泵故障診斷研究*

金林彩,葉杰凱,湯小明,趙 健,易燦燦

(1.麗水市特種設備檢測院,浙江 麗水 323000;2.武漢科技大學 機械自動化學院,湖北 武漢 430081)

0 引 言

隨著液壓技術的高速發展,憑借液壓元件精密度高、抗載荷和自動化等優點,目前,液壓系統已被廣泛應用于機床、化工和工程機械等領域。

作為液壓系統的核心,液壓泵是保證整個系統正常運行的關鍵,其健康狀態將直接影響大型裝備能否長期安全穩定地運行[1,2]。因此,及時迅速地對液壓泵的故障進行識別,對提高液壓系統運行的可靠性,降低其運行維護成本有著重要的意義。

在液壓系統的故障診斷中,基于振動信號的時頻分析是一種常用的檢測方法。液壓泵長期在變轉速與變負載的工況下運行,當其發生故障時,所測得的故障振動信號往往呈現非線性和非平穩的特性,再加上還有其他強噪聲等因素的干擾,因此,如何對液壓泵故障進行快速、準確地識別,并提取出有效的故障特征,一直以來都是液壓泵故障診斷的難點[3]。

經驗模式分解(empirical mode decomposition,EMD)是HUANG N E等人[4]提出的一種多分量信號自適應分解算法,其具有正交性、完備性等優點;雖然EMD在故障診斷領域已經得到了廣泛應用,但其存在模式混疊、包絡擬合以及對噪聲敏感性不足等問題[5,6]。JONATHAN S[7]提出了一種局域均值分解(local mean decomposition,LMD)方法,其在減少迭代次數、抑制邊界效應等方面要優于EMD;不過該方法也存在不少缺點,比如算法效率低、模式混淆等。

變分模式分解(variational mode decomposition,VMD)是DRAGOMIRETSKIY K等人[8]提出的一種新的自適應分解算法。該方法通過迭代尋找變分模型最優解,將振動信號分解為一組模式分量;同時在迭代過程中,不斷更新每個模式分量的中心頻率和頻帶,從而可以對振動信號進行自適應劃分[9]。

由VMD算法和基本原理可知,其分解結果受懲罰參數和分量個數的制約,且必須在開始分解之前確定模式數量。當設置模式的數量過高時,會出現一定的干擾模式,影響其對有效信息的提取;當設置模式的數量過低時,又會出現模態混疊現象[10]。

為了在液壓泵振動信號中更好地提取到其微弱的故障特征,需要對信號分解方法進行優化。在VMD的基礎上,研究人員又提出了一種新的模式分解算法,即變模式提取(VME)[11]。在采用VME對信號進行處理時,首先需要通過VMD將信號分解成各模式分量,然后利用Wiener濾波器對各分量進行濾波,最后根據得到的信號中心頻率近似值,對中心頻率附近的特定模式進行提取,且提取的該特定模式與經VMD分解后的其他模式分量無關。

與傳統的VMD相比,VME消除了對分量數量的限制,具有更高的收斂速度,同時也大大降低了提取特定模式分量的計算量。因此,VME在液壓泵故障診斷領域具有良好的應用前景。

近年來,有學者將非線性時間序列分析方法用于對振動信號的處理,通過提取標度指數來進行故障識別[12，13]。去趨勢波動分析(DFA)是PENG C K等人[14]提出的一種計算時間序列長程相關性標度指數的方法,其優點在于可以將不同階的外來趨勢項從時間序列中去除,還原時間序列本身所具有的統計行為特征。目前,DFA在氣象、金融和地震波等領域應用廣泛。MOURA E P等人[15]采用DFA對齒輪故障進行了識別,達到了故障分類和降維的目的,效果十分顯著。

另外,在數據降維方面,為了更好地保留局部重要幾何結構的數據,有別于傳統的主成分分析(principal component analysis,PCA)方法,HE X[16]提出了局部保留投影(locality preserving projection,LPP)法。該方法首先將高維度數據投影到低維子空間中,再對降維后的投影數據進行聚類分析,由此得到較好的聚類效果。在數據處理過程中,該方法不僅可以降低原始空間數據的計算復雜度,減少冗余信息對模型的干擾,還可以最大限度地保留局部數據結構中的有效信息,提高故障分類的準確率。

為此,在利用VME對信號進行模式分解的基礎上,筆者提出一種基于去趨勢波動分析與小波降噪的液壓泵故障信號降噪和故障模式分類方法。該方法首先通過VME對原始振動信號進行分解,得到多個不同的模式分量IMFs,再對中心頻率附近的特定模式分量進行提取,然后通過去趨勢波動分析(DFA)方法,區分有用信號分量和噪聲信號分量,最后對重構的信號進行多統計學特征計算和LPP降維,以實現對不同液壓泵故障類型進行聚類分析。

1 理論描述

1.1 變模式提取算法(VME)

對于輸入信號f(t),將其分解為期望模式ur(t)和剩余信號fk(t),則其表達式為:

f(t)=ur(t)+fk(t)

(1)

期望模式ur(t)應在其中心頻率附近,因此,可通過最小化,得到其表達式為:

(2)

式中:δ(·)—狄拉克分布;*—卷積;ωr—中心頻率;I1—期望模式的帶寬。

為實現完全準確的變模式提取,此處使用具有以下頻率響應的濾波器:

(3)

此外,為了使fk(t)與ur(t)之間的頻譜重疊最小化,使用以下懲罰函數,即:

(4)

式中:γ(t)—所用濾波器的脈沖響應。

在滿足式(1)的約束條件下,將I1和I2最小化,即:

(5)

式中:η—用于平衡I1和I2的參數。

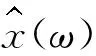
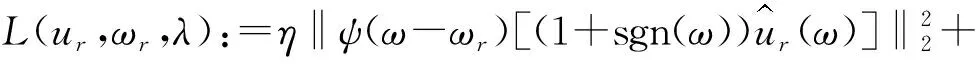
(6)

式中:λ—拉格朗日乘數。

使用乘數算法的交替方向法,即通過優化一系列迭代子,就可以解決最小化問題。第(m+1)次迭代中的期望模式函數可由以下表達式獲得:

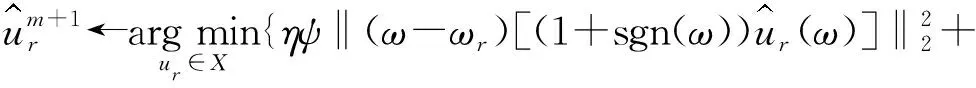
(7)

(8)

式中:m—迭代次數。

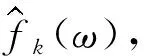
(9)

(10)

最后,通過對偶上升法,可得到拉格朗日乘數λ的簡化表達式:

(11)

式中:ζ—更新參數。

VME的具體實現過程如下:

(2)令m=m+1,并執行整個循環;

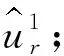
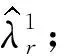
(6)設定值大于零的判別精度ξ,直到收斂滿足:

(12)

收斂滿足式(12)即可停止循環,輸出結果;否則重新回到步驟(2)重新運算。

1.2 去趨勢波動分析(DFA)

設存在時間序列x(t),t=1,2,3,…,N,對該序列進行去趨勢波動分析的步驟如下:

(1)求時間序列x(t),t=1,2,3,…,N的累積離差:

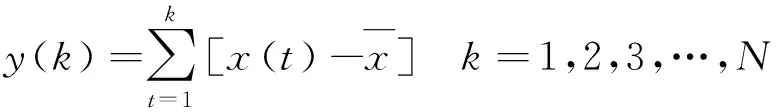
(13)

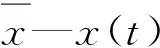
(2)將時間序列y(k)等分成Ns個不重疊的窗口,每個窗口包含s個采樣點,則Ns=[N/s]。

假設每個區間都具有一個有關時間t的p階趨勢,則每個窗口內的趨勢方程可表達為:

(14)

其中:通過對該窗口的數據進行最小二乘擬合,可以得到βj(j=0,1,2,…,p),則可得擬合曲線ys(k)。

(3)消除每一窗口時間序列y(k)的趨勢項ys(k):

Δys(k)=y(k)-ys(k)

(15)

(4)計算時間序列Δys(k)的二階波動函數:

(16)

(5)將窗口大小s按照一定步長遞增,重復步驟(2～4),可得到波動函數F(s)隨窗口大小s變化的曲線。

若該曲線服從冪律關系,則存在:

F(s)～sα?F(s)=Asα

(17)

上式表明,x(t)具有自相似分形特征。

分別求F(s)和s的對數,得到雙對數圖,則lg(F(s))與lgs呈現線性關系,其斜率便是尺度指數α,可用最小二乘法得到:

lg(F(s))=lgA+αlgs

(18)

1.3 局部保留投影(LPP)降維

令矩陣Z=(z1,z2,…,zn)∈Ra1×n為樣本集合(其中:n為樣本數,a1為樣本原始維度),則LPP的目標函數為:

(19)

式中:a2(?a1)—低維子空間維度。

原始空間數據投影到低維子空間中得到投影矩陣Q∈Ra1×a2。

相似性矩陣H∈Ra1×n的定義為:

(20)

式中:t—常量;τ—大于0。

經過變換與推導,LPP可定義為:

(21)

式中:L—拉普拉斯矩陣,L=G-H;G—對角矩陣。

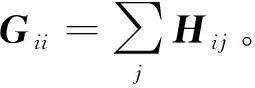
綜上所述,筆者所提出方法的具體實現步驟如下:

(1)對原始液壓泵振動信號x(t)進行變模式提取(VME),分解獲得一系列模式分量IMFi(i=1,…,n);利用去趨勢波動分析DFA的方法對分解的IMFi(i=1,…,n)計算標度指數αi(i=1,…,n);

(2)確定標度指數閾值θ,標度指數小于閾值θ對應著與噪聲相關聯的模式分量IMFp(p=1,…,t,t≤n),標度指數大于閾值θ對應著與噪聲無關的模式分量IMFq(q=1,…,e,e≤n,n=e+t);對IMFp進行小波降噪,抑制噪聲對高頻有用信號的干擾;

(3)將標度指數高于閾值θ的模式分量IMFq和小波降噪后的IMFp進行信號重構,然后對重構信號計算多個統計學特征,如平均值、有效值、峰值等,利用局部保留投影算法(LPP)對高維數據進行降維,從而完成對液壓泵不同故障模式的聚類分析。

筆者所提出的方法的技術路線圖如圖1所示。

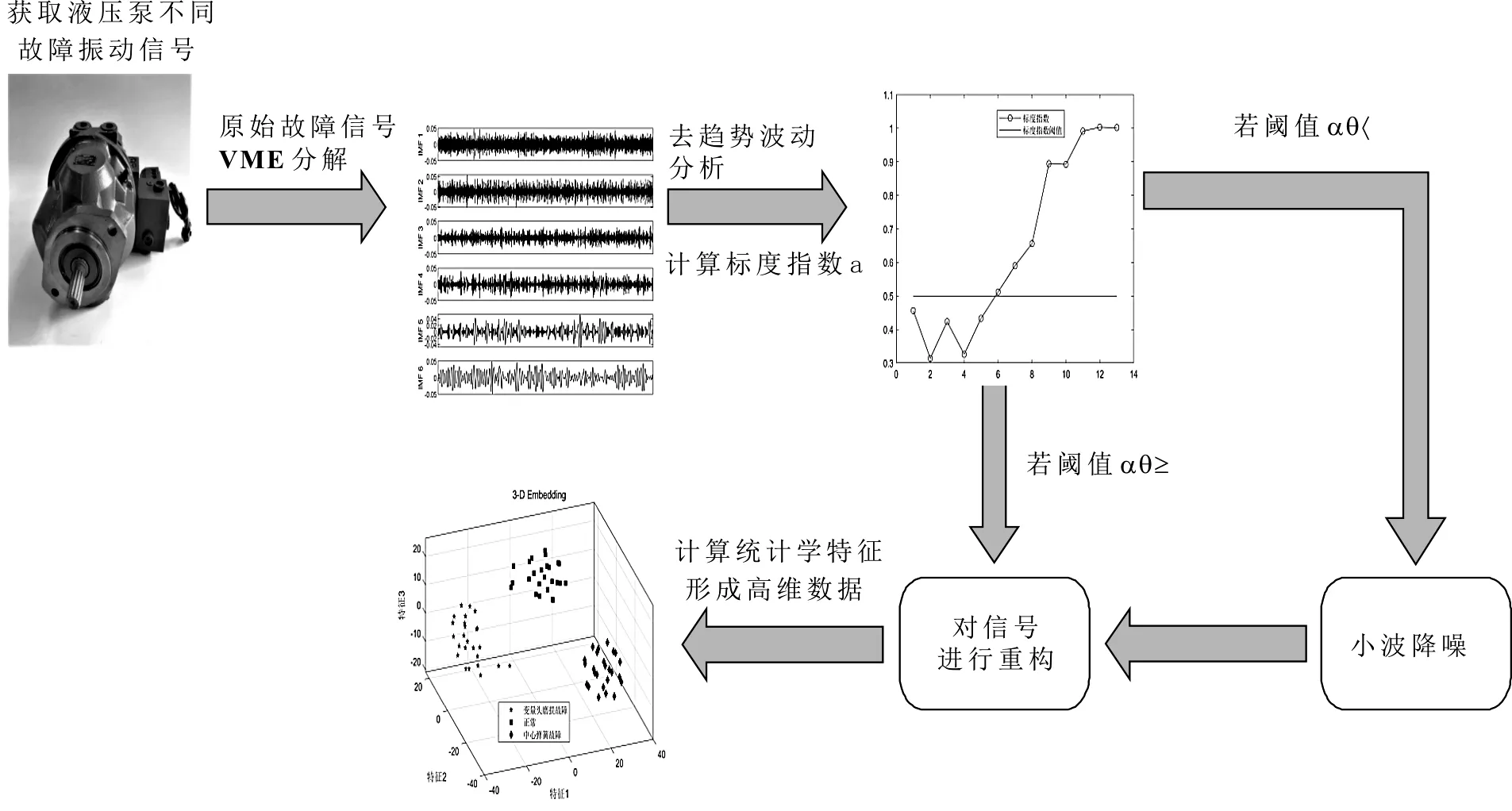
圖1 該方法的技術路線圖

2 液壓泵故障仿真信號分析

為了說明筆者所提出方法的可行性,筆者構造仿真信號進行了驗證,設置該仿真信號如下式所示:

I1(t)=3cos(60πt)
I3(t)=cos(100πt+10t)(3+sin(6πt))
I2(t)=cos(100πt+10t2)(3+cos(30πt))
I=I1+I2+I3+n(t)

(22)

式中:I—多分量調幅-調頻信號,I=I1+I2+I3。

為了評價方法的噪聲魯棒性,筆者對信號添加SNR=10 dB的高斯白噪聲。

仿真信號時域波形及其構成模式分量圖如圖2所示。

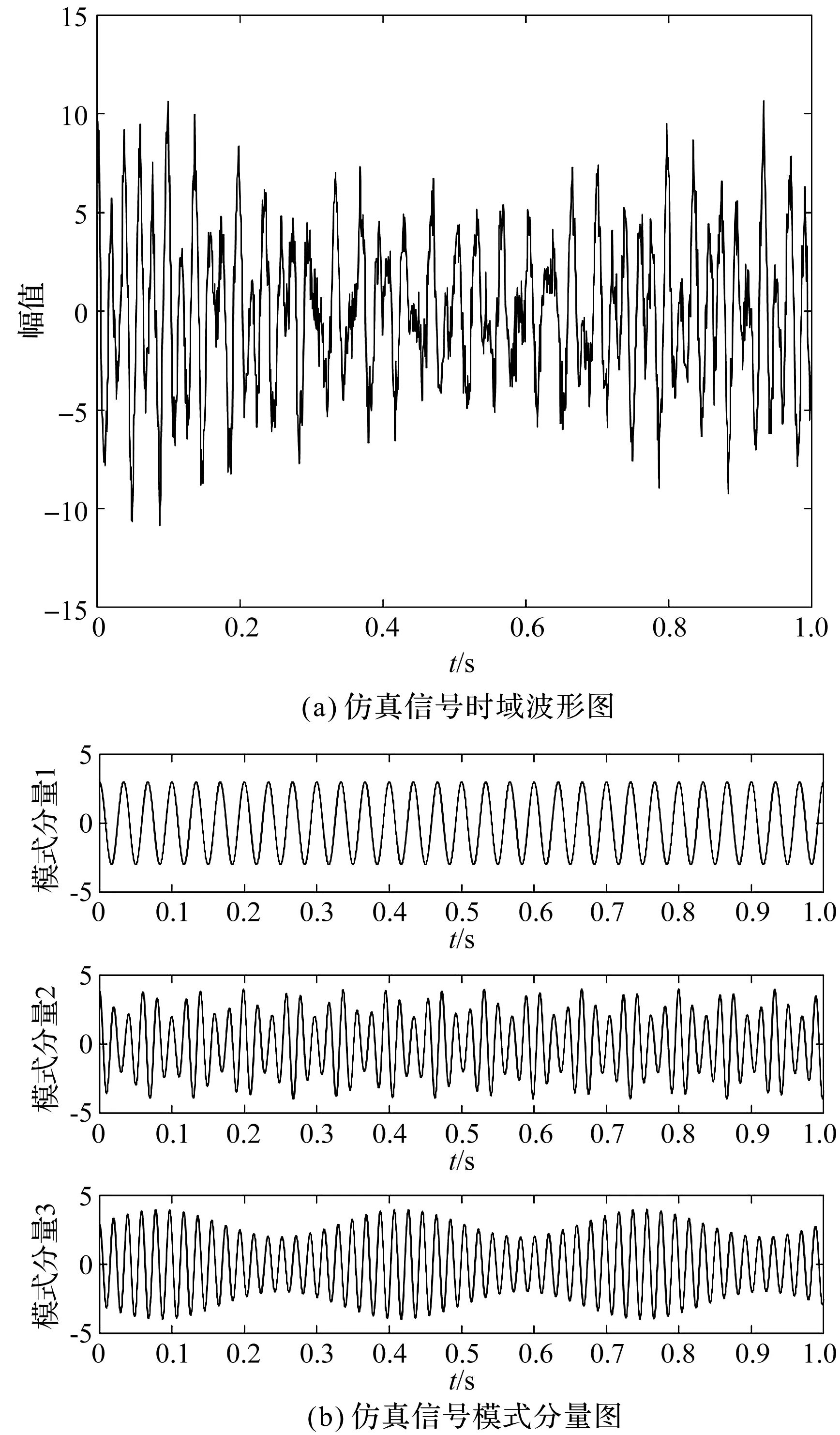
圖2 仿真信號時域波形及其構成模式分量圖

2.1 采用常用算法的分解結果

為了便于比較分析,筆者分別采用經驗模式分解(EMD)、局部均值分解(LMD)和變分模式分解(VMD)對仿真信號進行信號分解。

采用EMD、LMD和VMD的模式分解結果如圖3所示。

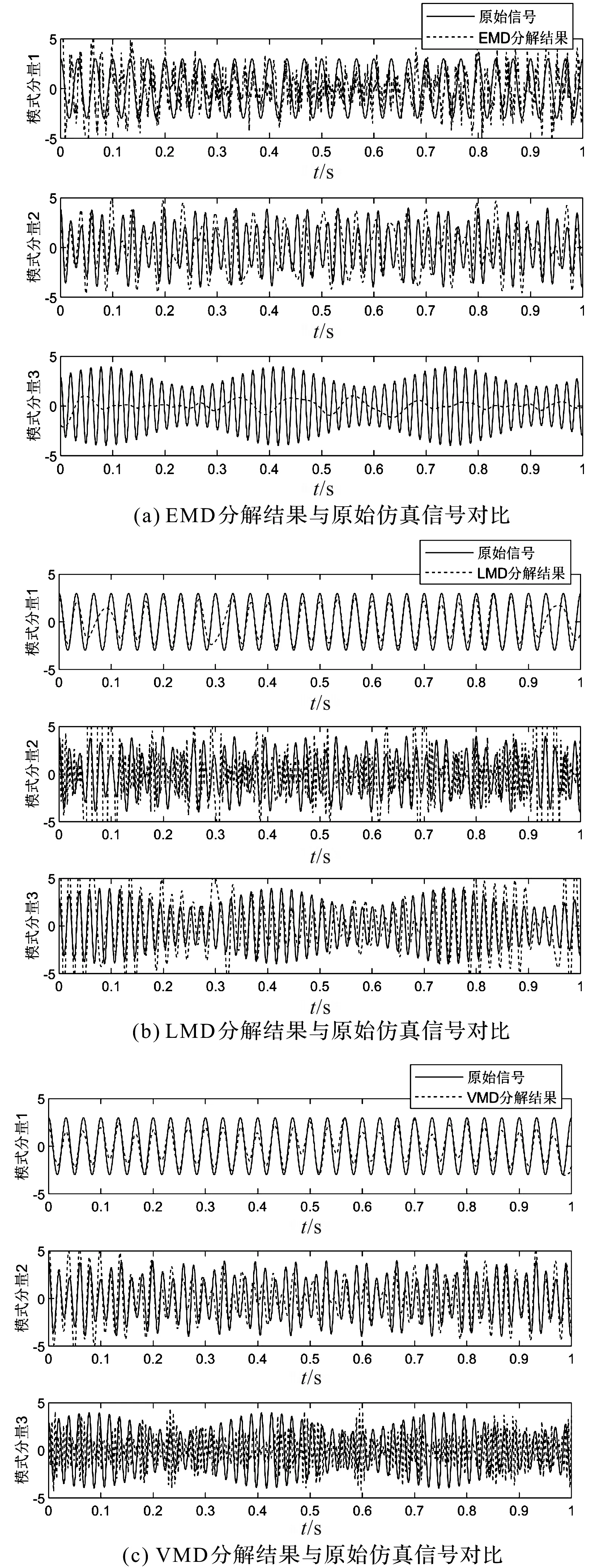
圖3 EMD,LMD和VMD的模式分解結果

從圖3中可以看出:由于受到噪聲的影響和理論方面的欠缺,上述常用的分解算法無法將3個模式分量準確地分解出來。

為此,筆者采用VME分解算法對仿真信號進行處理。

2.2 采用VME的分解結果

VME的模式分解結果與原始信號對比如圖4所示(圖中,虛線分量為VME分解后的結果,實線分量為原始仿真信號)。

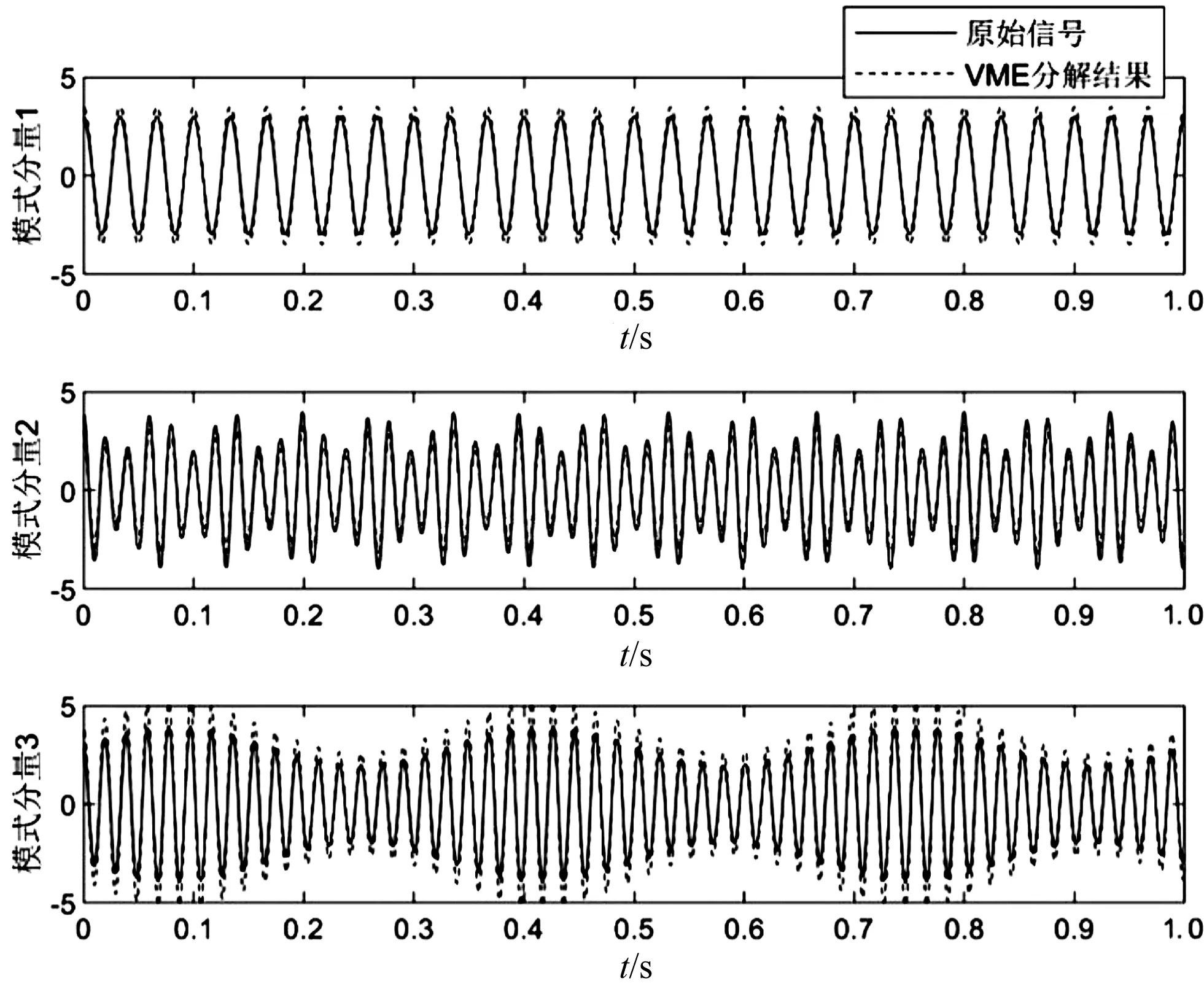
圖4 VME的模式分解結果及與原始仿真信號對比

圖4結果顯示:VME更準確地實現了信號的模式分解,更好地保留了信號各分量的特征。

筆者根據分解結果與原始信號的偏差大小,計算各分解算法模式分解的均方根誤差(RMSE)。

各算法分解結果的均方根誤差如表1所示。

表1 各算法分解結果的均方根誤差

通過以上比較可知:VME相較其他經典分解算法具有更好的分解效果,將其應用于液壓泵振動信號分析,可以有效地實現對故障特征的識別及提取。

3 實驗及結果分析

為了驗證上述方法的有效性,筆者通過軸向柱塞泵液壓實驗系統,來對采集到的振動信號進行分析處理。

3.1 故障實驗

該試驗裝置為斜盤式軸向柱塞泵,型號為25YCY14-1b,柱塞數為7。在實驗過程中,筆者分別采集正常狀態、變量頭磨損故障、中心彈簧故障的泵殼振動信號,通過本文提出的方法實現液壓泵3種不同故障模式的分類。

液壓泵故障實驗臺結構簡圖如圖5所示。

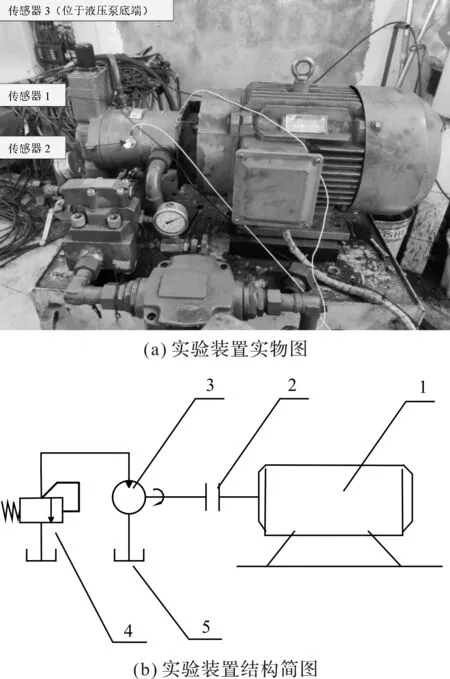
圖5 液壓泵故障實驗臺結構簡圖1—電機;2—聯軸器;3—液壓泵;4—溢流閥;5—油箱

液壓泵試驗參數設置表如表2所示。

表2 液壓泵試驗參數設置表

實驗測得液壓泵不同故障類型信號的時域圖如圖6所示。

然后,筆者對振動信號進行變模式提取(VME)分解。

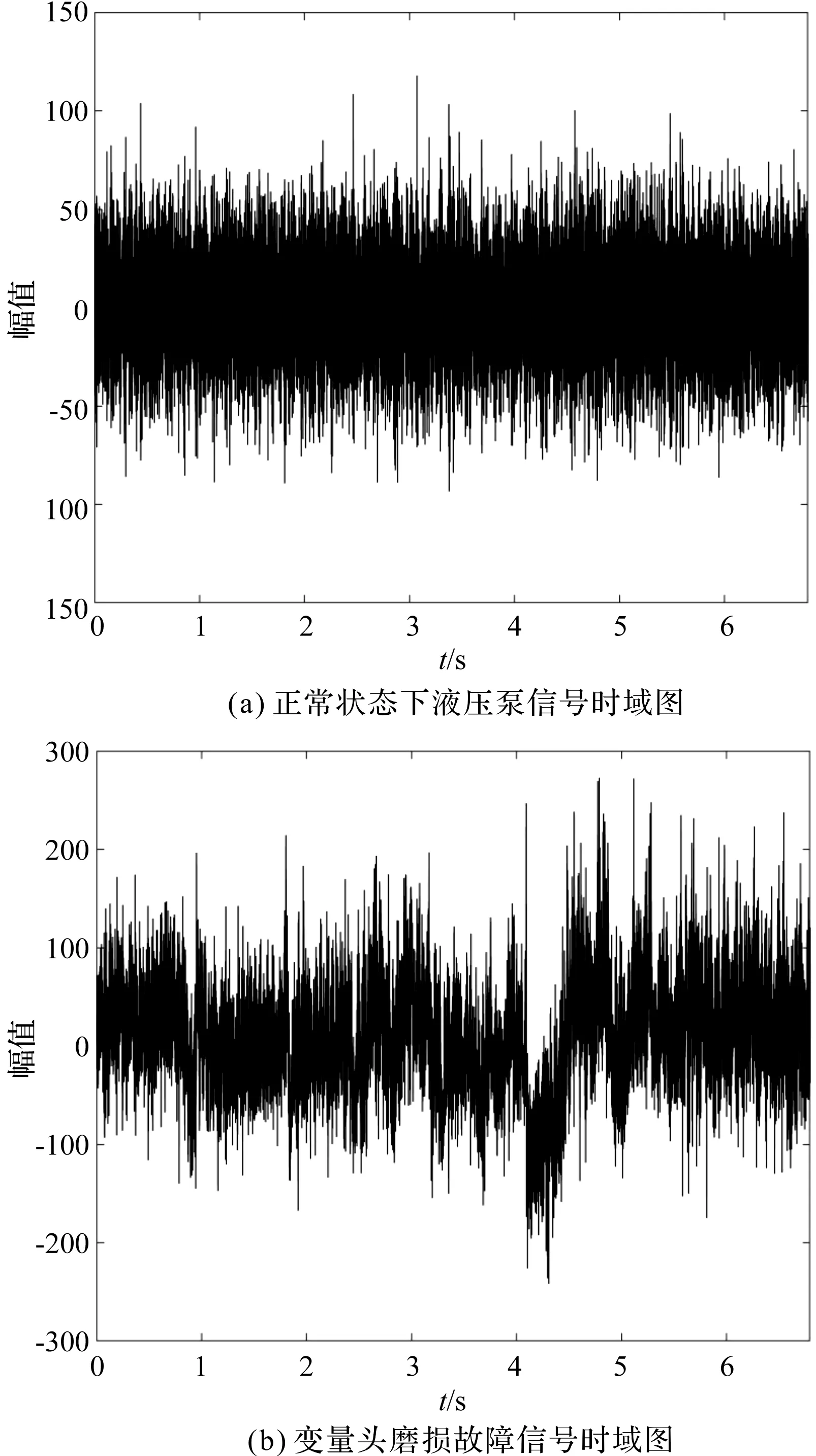
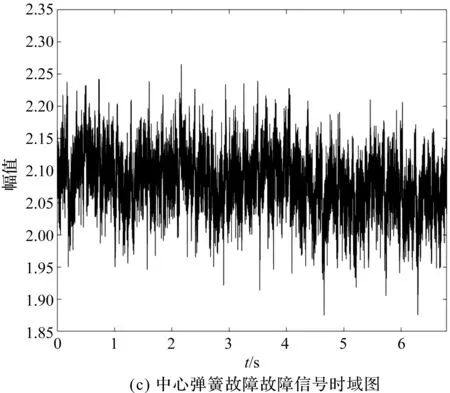
圖6 液壓泵不同故障類型信號時域圖

液壓泵不同故障類型信號VME分解示意圖如圖7所示。

最后,筆者利用所提出的方法,對VME分解后的信號進行去趨勢波動分析,其中,標度指數的閾值設定為θ=0.5。

分解后得到的模式分量標度指數分布圖如圖8所示。

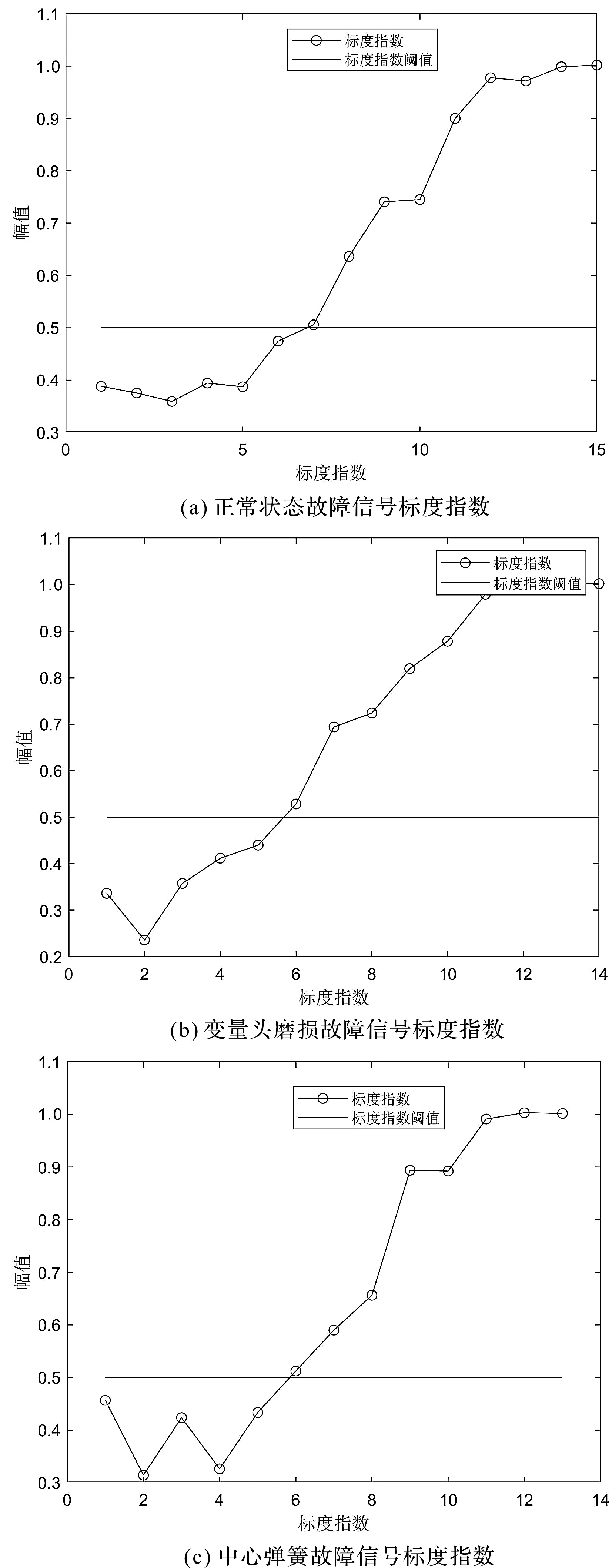
圖8 分解后模式分量標度指數分布圖

通過圖8可以發現:前面分解得到的模式分量的標度指數都要低于閾值θ=0.5,因此,有必要對其進行降噪處理,然后進行信號的重構,以獲得具有較高信噪比的液壓泵振動信號。

同時,筆者通過計算平均值、有效值、峰值、方根幅值、歪度、峭度等16個重構的時域特征參數,形成高維的數據結構,并在高維空間進行LPP降維聚類。

采用筆者提出的方法對液壓泵故障進行分類識別,所得的結果如圖9所示。

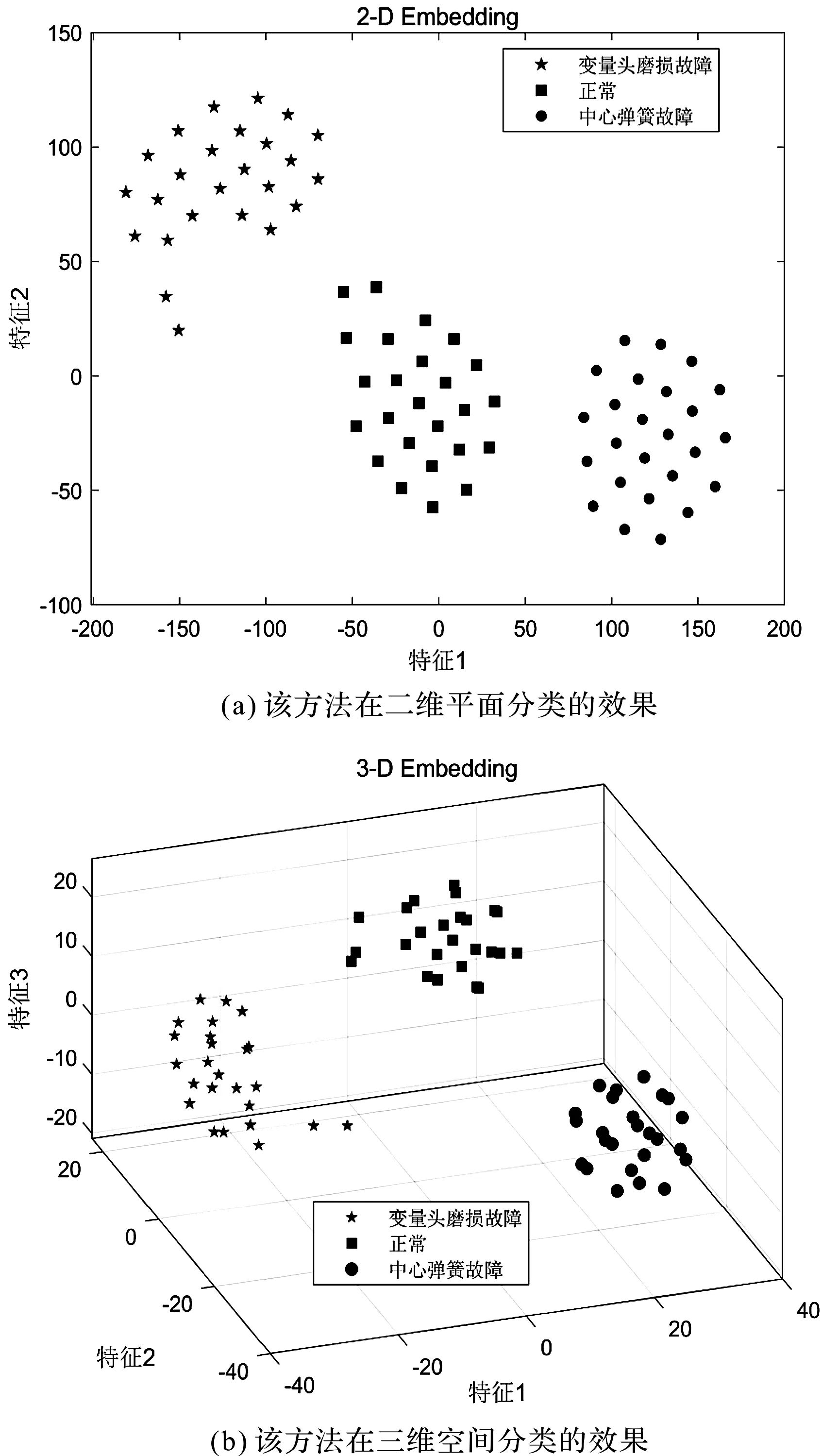
圖9 該方法對液壓泵故障分類的結果

3.2 對比分析

為了進一步說明該方法的有效性,筆者不用變模式提取(VME)方法和去趨勢波動分析(DFA)的手段進行信號的分解和重構,而直接利用經典的PCA及LPP算法對原始數據進行多統計學特征計算,并進行降維聚類。

筆者采用其他降維方法對液壓泵故障進行分類識別,所得的結果如圖10所示。

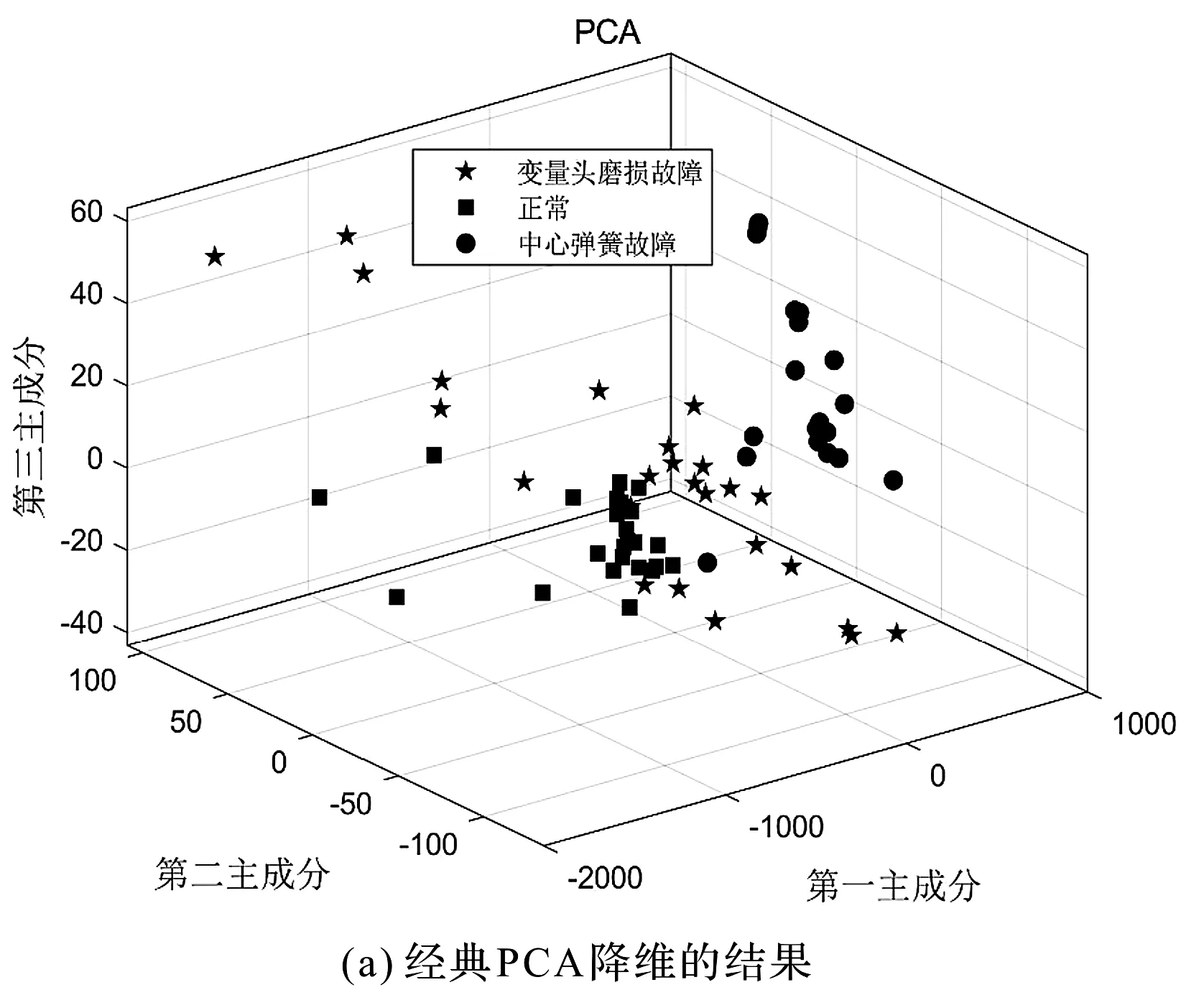
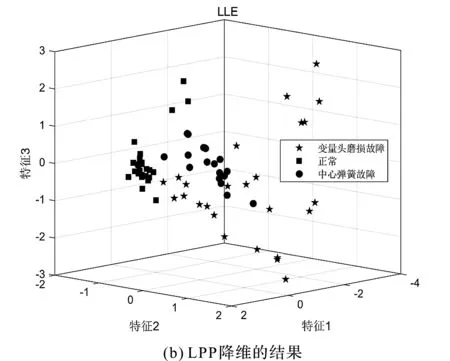
圖10 其他降維方法對液壓泵故障分類的結果

通過對比圖9與圖10可以看出:筆者提出的聯合VME方法和DFA的方法,在液壓泵故障信號降噪和降維處理上具有更佳效果,能夠對多個不同故障類型的振動信號進行準確識別。

4 結束語

為了解決液壓泵故障診斷識別精度不高的問題,筆者提出了一種基于變模式提取(VME)與去趨勢波動分析(DFA)的信號去噪方法,并利用局部保留投影(LPP),實現了對液壓泵不同故障類型的準確聚類。

該研究的主要內容和結論如下:

(1)利用變分模式提取(VME)的方法對液壓泵振動信號進行了模式分解,消除了分解過程中對分量數量的限制,提高了其運算效率;

(2)通過去趨勢波動分析(DFA)方法,對提取的模式分量計算相應的標度指數,利用標度指數作標準來判斷是否運用小波降噪進行處理,并通過LPP算法對數據進行了降維和聚類分析;

(3)將筆者所提方法應用于液壓泵故障實驗臺振動信號分析,結果表明,該方法可以作為機電系統液壓故障診斷的一種手段。

在后續的研究中,筆者將針對二元甚至多元的VME,推導出多元變分模式提取算法,并將其應用于機電系統故障診斷中。