影響顎式破碎機破碎腔分層的參數研究

熊紹俊，何志敏，姜俊雄

（南昌礦山機械有限公司，江西 南昌 330004）

以顎式破碎機作為研究方向，以往行業多以工作人員工作經驗作為整機機構設計依據，并沿用簡擺式破碎機相關方法，但是近年來，以行業技術發展作為背景，該方法的應用將難以滿足當前顎式破碎機設計精確性要求，因此，工作人員應以破碎腔分層著手，明確具體影響參數，應引進計算機仿真技術，完成數學模型構建，落實主軸轉速設計工作，提升顎式破碎機性能。

1 顎式破碎機破碎腔分層概述

1.1 顎式破碎機工作原理

在各類顎式破碎中，復擺顎式破碎機常見度較高，也是本文的研究項目。其組成主要包括定顎板、動顎板兩個部分，前者主要在機架前壁安裝，而后者主要負責完成周期性往復運動。兩者之間另外存在18°～22°的夾角，其中，如果設備為中型，則取值為18°～20°，如果設備屬于中小型設備，取值為20°～22°。兩者之間還另外存在工作區間，完成物料破碎處理[1]。

該設備工作原理如下：可將設備進一步向曲柄搖桿機構進行簡化。其中，曲柄部位、動顎部位以及肘板分別為主軸以及連桿、搖桿，借助曲柄，可有效推動動顎工作，并完成周期性往復運動。在給料口中，設置其與定顎之間的最遠距離為E0，將動顎松邊設置為E0MO。在排料口中，將其與定顎最遠位置設置為M1，則動顎緊邊設置為E1M1。當動顎運動趨勢為從緊邊到松邊，則在這一階段，物料處于下降狀態，而反之物料將會受到擠壓影響，導致破碎，最終在破碎腔中排出。

1.2 破碎腔分層理論

針對傳統破碎腔分層，如果動顎向緊邊運動，在擠壓的作用下，物料將會被破碎處理，并在動顎返回過程中，呈現下落狀態，直到再次相遇，在這一過程中，掉落距離與破碎層高度相符。分層理論存在以下問題，例如：①如果動顎、動顎在物料下落過程中高度相同，不考慮動顎對物料造成的影響，保持定額不動狀態，當物料進入到定顎處，在重力的作用下，物料將會呈現下拋運動狀態，導致不同位置物料位移不同。②傳統分層形式對壓實點的認識相對偏頗，認為不同動顎點位進入壓實點時刻相同，而本文研究顯示，對比進入壓實點時間，排料口優先于給料口。

2 影響破碎腔分層參數

通過在分析動顎運動方式的同時，完成物料運動方式分析，經實時仿真，可對物料下落情況進行模擬，并完成破碎腔分層工作，確保能夠建立出完整的分層模型。下文將進一步對分層影響參數進行分析，并借助相應的軟件，完成權重分析。

2.1 構建分層模型

本文研究使用曲柄轉速規格為240r/min。在動顎物料中，需要將初始速度設置為豎直分量，并進一步進行下拋運動處理。確定下分界點為排料口，并逐步按照向上方向完成尋找，如果物料在動顎附近下落，則需要在一段時間后，進入到下分界點運動軌跡中，并在動顎擠壓處理下，實現破碎，進而形成上分界點。借助這一方法，可逐步確定動顎分界點[2]。

如果定額傾角不計入到影響因素中，將定顎物料進行自由落體運動，如果物料層數相同，則下落時間也處于相同狀態。設置下分界點為排料口，則需要按照向上的方向，尋找分界點位置，連接相同層數的動顎以及定顎，進而實現破碎腔分層。

2.2 分層影響參數

2.2.1 主軸轉速

保持相同幾何參數，確保外部條件一致，將曲柄轉作為唯一變量，可具體對分層、轉速之間的影響進行判斷。在曲柄轉速中，區域范圍為150r/min～200r/min，分層可達到6層，而區域范圍為200r/min～250r/min，分層在2～5層，區域范圍低于100r/min，分層受影響較小，區域范圍高于250r/min，同理。

2.2.2 四桿機構

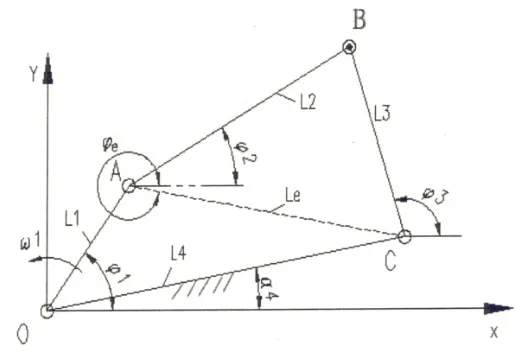
圖1 復擺顎式破碎機四連桿機構示意圖

在顎式破碎機中，針對四桿機構，其尺寸以四部分為主，即L1、L2、L3、L4，其中，L1為曲柄，位于主軸AO中，L2為連桿，位于動顎AB處，L3為搖桿，位于肘板BC處，L4位于機架CO處。而上動顎板尺寸包括4個部分，即L5、L6、L7、L8，不改變其他參數，分別以L1、L2、L3、L4、L5、L6、L7、L8作為變量，完成破碎腔層數分析。

不改變其他參數，單一改變曲柄L1桿長，改變長度范圍為10mm～20mm，觀察破碎腔分層情況。分層數將會隨著桿長增加而呈現整體縮小趨勢，當桿長為10mm～14mm范圍內，層數未出現明顯變化，而當桿長為15mm～19mm范圍內，層數出現明顯減少趨勢。

法國加利埃尼將軍巧用摩托化運兵術使法軍化險為夷。幾天前，他已命令組織一支出租汽車運輸車隊。但是到了1914年9月6日，他看到已經組織的出租車數量實在是太少了，必須立即將所有可以利用的出租車改做運兵車。晚間8時，將軍決定組織一支出租車大軍，運送上萬名官兵趕赴前線。

保留其他參數不變，單一改變連桿L2桿長，試驗調整范圍為1400mm～1500mm，觀察破碎腔分層情況。結果顯示，在L2桿長增加的情況下，破碎腔整體呈現減少狀態。具體而言，當桿長處于范圍1410mm～1440mm，層數并未發現明顯變化，而當范圍提升到1450mm～1500mm，層數開始逐步縮小。

其他參數不發生變化，僅改變搖桿L3桿長，調整范圍保持在450mm～650mm，對破碎腔分層情況進行觀察。當桿長范圍為450mm～570mm，分層呈現增加趨勢。當桿長范圍為630mm～650mm，則分層將會呈現輕度下降。在桿長增加的情況下，整體分層處于先增大、后減小的狀態。其中，層數增加桿長范圍為450mm～550mm，層數減少桿長范圍為550mm～650mm，層數峰值桿長長度為550mm。

如果不變化其他參數，在150mm～300mm范圍改變桿長L5，在桿長增加的情況下，分層將會出現數量減少趨勢。而在400mm～500mm范圍內改變桿長L6，在桿長增加的情況下，分層呈現整體增加現象。

其他參數均不作改變，調整桿長L7，長度調整范圍為400mm～500mm，分層數量不變桿長范圍為400mm～480mm，而分層從18層到20層桿長范圍為480mm～500mm。調整桿長L8，長度調整范圍為600mm～750mm，分層數量與桿長呈正相關關系，即桿長提升，分層也隨之上漲。

2.3 影響分層因素權重

以上文參數分析作為依據，本文進一步對各項因素影響權重展開分析，因為破碎腔分層涉及參數較多，影響因素也相對較多，僅通過觀察，難以得到準確結論，因此，本文主要借助SPSS Modeler軟件，完成各項數據分析工作。

具體而言，需要先構建出完成的數據流模型，并將上文獲取到的表格帶入到SPSS Modeler軟件中，選擇訓練分區（訓練函數模型）占據70%，選擇測試分區（校驗函數模型準確性）占據30%。前者主要在軟件神經網絡模塊中訓練權重，將各因素輸入后，隨機賦予權重，以W1～W9表示。借助加法器，并配合使用激活函數，可有效獲取分層數，由于數據與仿真分層數相對應，而借助賦予權重，兩者將會存在偏差情況。因此，需要合理調整賦予權重，確保實際分層數與仿真分層數相接近，在最大程度上控制誤差值。

以神經網絡模塊展開分析，在參數方面，完成各因素輸入工作，并將實際分層數設置為目標，共包括兩種神經網絡，即BP、RBP，本文主要應用前者，點擊后，經處理，模塊自動生成預測變量。

針對神經網絡隱藏層，其共包括破碎層7個，經誤差處理，最終模型準確度較高。結合本文研究顯示，對比各類分層影響因素，轉速影響最高，可達到0.46，其余影響因素均處于0.2以下，與動顎上尺寸相比，四桿機構影響因子相對較高。

在完成模型構建后，為有效實現賦予權值檢驗工作準確性，可借助測試分區完成。其中，以仿真分層數為水平坐標，以預測分層數為縱坐標，兩組數據越接近，則說明準確性越高，經檢驗y=x，證明本文研究數據具有良好的可靠性。

基于動顎分界點尋找，需要確定像雨點位置，并集中對物料下落方式進行探索，借助有效方法，確保仿真速度顯著提升。同時，利用SPSS Modeler，可具體判斷分層影響參數，最終得到結論如下：轉速與破碎腔層數呈正比例關系，如果轉速提升，破碎層也會呈現增加趨勢，具體影響因子為0.46。

3 結語

綜上所述，借助MATLAB，可完成破碎腔分層模型構建，并具體對主軸轉速與分層之間的影響進行分析，判斷相關幾何參數。在其他分層影響因素中，其因子均處于0.2以下，并且與動顎結構尺寸相比，四桿機構具有更高的影響因子。