兩直線斜率積問題分類解析與命題推廣
武 剛 李秀元
(1.湖北省武穴中學 435400;2.湖北省武穴市實驗高級中學 435400)
平面解析幾何的教學,從知識層面上講,需要掌握直線、圓及圓錐曲線的定義、方程和幾何性質,熟悉直線與二次曲線位置關系問題的處理方式;從思想方法層面講,主要是傳授數形結合與模型化思想;從能力層面,包括但不僅僅限于發現問題、提出問題,語言表達以及運算與推理等能力培養;從核心素養層面,則需重點提升直觀想象、數學運算、數學建模、邏輯推理和數學抽象素養,其中,數學運算尤為突出,很多結論的獲取,都是基于計算結果,解題過程大部分是運算過程展示.在圓錐曲線的學習過程中,我們發現,兩直線斜率積問題比較常見,從課本到高考都有體現,試題大致可分為四類:已知過動點兩直線斜率積為定值,求動點軌跡方程;已知動直線與圓錐曲線相交于兩點,兩點所對應的兩條直線斜率積為定值,研究動直線的特點;證明兩直線斜率積為定值;在兩直線斜率積為定值的基礎上,探討直線方程中參數關系等.
一、已知斜率積求動點軌跡方程

(1)求動點P的軌跡C的方程;
(2)已知直線l:y=kx+m,C的右焦點為F,直線l與C交于M,N兩點,若點F是△AMN的垂心,求直線l的方程.
分析這類題是課標實驗教科書《數學》(選修2-1)中例題的變式.課本例題可以看成產生橢圓的一種方式,揭示了橢圓的一條性質.
因此,基于兩個關于原點的對稱點,若兩動直線斜率之積為定值(負值),則動點軌跡一定是橢圓(除去兩已知點).應用模型識別,我們可以提前定位曲線類型,識別方程結構.
本題條件直譯后,化簡即得動點軌跡方程,但在表示斜率時要注意坐標的限制條件,即軌跡方程的限制條件,而第(2)小題,則需要借助互相垂直的兩直線斜率之積為-1來轉化運算.







反思橢圓這一性質的產生,應該源于任一直徑所對圓周角為直角,且互相垂直的兩直線斜率之積為定值-1的基本事實.圓和橢圓同屬于二次曲線,兩者之間可以互相轉化,進行類比推理,從特殊入手,進而得到橢圓的一般化命題.橢圓具有的性質,雙曲線也會有類似的性質,我們要做的只是想辦法將它們統一起來.在圓錐曲線章節復習時,以課本例習題為載體,設置一次探究活動,重點關注性質的產生過程與整合,對落實邏輯推理、數學抽象和數學運算等核心素養意義非凡.
二、探討或證明兩直線斜率積為定值


圖1
(1)求橢圓C的方程;
(2)設點P是橢圓C上異于A,B的點,與x軸垂直的直線l分別交直線AP,BP于點M,N,求證:直線AN與直線BM的斜率之積是定值.


反思由于定值結構形式與橢圓性質一致,二者之間應該有一定的聯系.事實上,如果將AN和BM延長,設交點為Q,只要能說明點Q在橢圓上,或者由直線BM與橢圓交于另一點Q,能說明A,N和Q三點共線,則兩個問題也就合二為一了.由于是純字母運算,無論是運算方向的把握,還是運算過程的落實,難度值都是很大的.但經過核算,這是對的.因此有

我們甚至可以更大膽地猜想,將橢圓長軸換成任一直徑,直線l與直徑垂直,所得兩直線斜率之積也是定值,讀者不妨試一試.
下面繼續來看斜率積為定值的其他形式的問題.
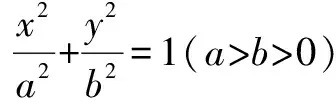
(1)求橢圓的方程;
(2)圓C的方程為x2+y2=5,若圓C與直線l相交于P,Q兩點(兩點均不在坐標軸上),試探究OP,OQ的斜率之積是否為定值?若是,求出此定值,若不是,請說明理由.


(2)當直線l的斜率存在時,設l的方程為y=kx+m,

因為直線l與橢圓C有且只有一個交點,所以Δ1=(8km)2-4(1+4k2)(4m2-4)=0,即m2=1+4k2.


設直線OP1,OP2的斜率分別為k1,k2,則



結果同樣與橢圓性質形式一致.一般地,我們有
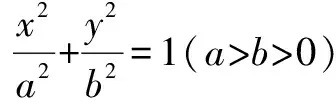
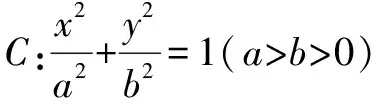
(1)求C的方程;
(2)直線l不過原點O且不平行于坐標軸,l與C有兩個交點A,B,線段AB的中點為M.證明:直線OM與直線l的斜率乘積為定值.

(2)設直線l:y=kx+t(k≠0,t≠0),A(x1,y1),B(x2,y2),M(xM,yM).


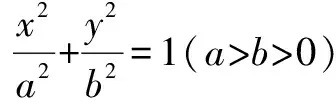
三、基于兩直線斜率積為定值,研究動直線特點

(1)求橢圓C的標準方程;
(2)設點Q是橢圓C與x軸正半軸的交點,斜率不為0的直線l與橢圓C交于不同的兩點D,E,若kQD·kQE=9,問直線DE是否恒過定點?若過定點,求出該定點的坐標;若不過定點,請說明理由.






所以y1y2=9(x1-1)(x2-1)=9(ty1+m-1)(ty2+m-1),進一步整理,得(9t2-1)y1y2+9(m-1)t(y1+y2)+9(m-1)2=0.

因為m≠1(直線不過(1,0)點),故有(9t2-1)(m+1)-18mt2+3(m-1)(1+3t2)=0,解得m=2.
故直線DE恒過定點(2,0).
四、基于兩直線斜率積為定值,研究動直線方程中參數的特點
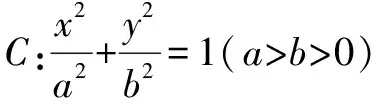
(1)求橢圓C的標準方程;




依題意,Δ=(8km)2-4(4k2+1)(4m2-4)>0,化簡,得m2<4k2+1.①

所以y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.

所以(4k2-5)x1x2+4km(x1+x2)+4m2=0.



雖然我們對一些命題進行了推廣,但也只是一般化而已,如果能在不同曲線上展現,這樣的研究也許更有意義.不管是哪種類型,問題解決最終都是展現數學運算能力,因此,在平時的解題教學中,除了邏輯分析外,還是需要留足時間,展示運算過程,突破運算技巧,提升運算能力.

