誰是世界上第一位數學家

□文/張天蓉

數學有著久遠的歷史。從原始社會開始，人類就在繩子上打結，以便記數；在地上畫圖，測量大小。“結繩計數”開創和發展了數字的最早概念，“土地測量”等生產活動的需求使幾何學應運而生。

如今，找到最多、最早數學記錄的地方，是古埃及和古巴比倫。目前最古老的一批數學文本，包括《普林頓322》（古巴比倫，約公元前1900年）、《萊因德數學紙草書》（古埃及，公元前2000年—公元前1800年）以及《莫斯科數學紙草書》（古埃及，約公元前1890年）。以上古文本中，都有關于幾何最早的記錄。

這應該算是人類最早期的數學。但是，古埃及和古巴比倫的資料有限、人物不詳，因此追溯數學歷史之源，還是從古希臘開始比較合適。

《普林頓322》泥板

《萊因德數學紙草書》

古希臘的天時地利人和

當今世界的人口超過70億，根據人類演化歷史的研究及現代DNA技術的追蹤，這幾十億的人口卻是來源于一個共同的祖先：非洲人。

后來，人類的祖先以雙腳走出非洲，遍游世界，將后代延續繁衍到地球各處。再后來，人類逐漸沿河而居，聚集在一起，建立了城市和國家，并因此獨立誕生了好幾個文明古國。

盡管多種人類文明獨立誕生于不同的地區，各自特色不一，但是作為人類文明思想精華之一的科學，卻是起源于古希臘！

科學之起源與數學思想的發展密切相關，如今被稱為人類第一位數學家的先賢叫泰勒斯，或稱“米利都的泰勒斯”。米利都是泰勒斯的家鄉。

那么，科學為何獨獨誕生于古希臘而非別處？答案有些出乎人們的意料，其原因竟然與古希臘的地理環境有關！

事實上，公元前600年—公元前500年，人類幾大古文明社會不約而同地出現了一段興旺場面：思想家輩出，哲學派別林立，各具特色和風格。然而同時，隨著各方宗教思想的嚴密化和系統化，東西方哲學思想開始分道揚鑣。這就是被后人稱為“軸心時代”的年代，被描述為人類文明歷史上“最深刻的分界線”。

那段時期，中國有孔子、老子、墨子、莊子、列子等諸子百家，印度有釋迦牟尼，波斯出現了拜火教……人類的幾大古文明社會開始通過不同的哲學反思來認識和理解這個世界。

大多數這些文明古國都始于農業的發展，建立于江河流域，而古希臘并不具備這種條件。例如，泰勒斯的家鄉米利都位于愛琴海東部沿岸，屬于古希臘愛奧尼亞群島一帶。那兒沒有河流只有海洋，沒有平原只有山地。

因此，古希臘一不傍河，二無森林，既未發展出如四大文明古國那種農業文明，也不可能有像瑪雅文化那樣的叢林文明。

然而，古希臘卻自有其“天時地利人和”！特殊的地理環境，使它盡管沒有“原生文明”，卻孕育出了一種獨一無二的、崇尚自由思想、有著海洋色彩的“次生文明”。

古希臘的思想家在多方文明的環繞滲透下，既保持其特有的自由思想，又包容地大量汲取外來的養分，最終化劣為優、揚長避短，讓科學發端于古希臘。

第一位數學家何許人也

古希臘數學家泰勒斯是西方思想史上第一個有記載、有名字留下來的思想家，被譽為世界第一位數學家、哲學家、科學家。泰勒斯對科學作了哪些貢獻？

泰勒斯證明了“泰勒斯定理”，首開先河引進“證明”的思想，將數學從經驗上升為理論，繼而使理性精神發源于古希臘，之后又傳播到歐洲并催生了現代科學。

泰勒斯出生于米利都，盡管當年這個城邦名義上被波斯統治，但實際上具有很大的獨立性。米利都的大多數居民是在公元前1500年左右從克里特島遷來的移民。克里特島在米利都的西南方，位處古埃及、古巴比倫文明的輻射范圍以內。而到了泰勒斯的父母一代，他們原是東南方向善于航海和經商的腓尼基人，也算是奴隸主貴族階級。因此，天才的泰勒斯從小受到良好的教育。

泰勒斯早年隨父母經商，曾游歷埃及、巴比倫、美索不達米亞平原等地。泰勒斯興趣廣泛，涉及數學、天文觀測、土地丈量等各個領域，游歷過程中學到很多知識。

泰勒斯最著名的哲學觀點是“水是萬物之本”。他研究天文，確認了小熊座，估量太陽及月球的大小，修正一年為365日。他還將從埃及祭司那里學到的數學知識應用于測量，估算船只離岸的距離，通過金字塔的陰影計算其高度，證明了泰勒斯定理。

泰勒斯也在民間留下了很多軼聞趣事。據說，有一次泰勒斯用騾子運鹽，一頭騾子不小心滑到溪水中，背上的鹽迅速溶解了一部分，于是這頭狡猾的騾子每到溪水旁就打一個滾，故意讓鹽溶解以減輕負擔。泰勒斯發現了這點，便將計就計，有時讓這騾子改馱海綿。騾子到溪邊照樣打滾，卻發現負擔越來越重。最后，聰明的泰勒斯終于使那頭騾子改掉了溪邊打滾的習慣，老老實實地繼續馱鹽！

泰勒斯還有幾個預言成真的故事。他曾經預言有一年橄欖會豐收，并搶先購買了米利都所有的橄欖榨油機，抬高價格壟斷了榨油行業，于是大賺了一筆。他以此證明自己如果把心思放在經商上，有潛力成為一個精明的商人。

據說，泰勒斯還利用他學到的天文知識，預測到了公元前585年的一次日食。那年，米堤亞和呂底亞的軍隊正準備打仗，泰勒斯的預言阻止了這場戰爭，因為當時人們將日食視作上天將懲罰人類的一種警告，交戰雙方自然不愿違背天意，于是便簽訂了停戰協議。根據現代天文學的知識，那是公元前585年5月28日的日食，泰勒斯應該無法準確地給出日期，只能預料一個大概的年月而已。

泰勒斯通過金字塔的陰影估算出金字塔的高度

邏輯推理和證明的意義

泰勒斯對數學的貢獻

泰勒斯在數學方面做了不少工作，從具體實踐到數學思想都有所貢獻。

實用計算

泰勒斯利用學到的幾何學知識，發展了以幾何物件的相似為基礎，計算一些無法直接測量的高度或距離的方法和技巧。例如，他測量了自己和金字塔的影子長度，以及自己的身高，并運用相似形的原理來測量金字塔的高度。泰勒斯亦根據此原理推算自己與海上船只的距離，以及推算懸崖的高度。

幾何證明

泰勒斯在進行幾何研究中，通過演繹推理得出許多數學定理和命題。其中，最典型的一個稱為泰勒斯定理。

泰勒斯定理講的是：“直徑所對的圓周角是直角。”泰勒斯并非此定理的首名發現者，古埃及人和古巴比倫人一定已知這特性，可是他們沒有給出證明。

理性精神

泰勒斯定理的證明是很容易的，屬于初中平面幾何的范圍。但泰勒斯對數學的貢獻不是在于幾何證明本身，而是在于引進了“證明”的方法和概念。要知道，在泰勒斯之前，已經有一大堆幾何事實，但沒有任何“證明”。泰勒斯是已知的第一個將演繹推理應用于幾何的人，在一個充滿謬誤和迷信的時代，他是第一個用邏輯推理來理解這個世界的人，這就是為什么他被認為是第一位真正的數學家。

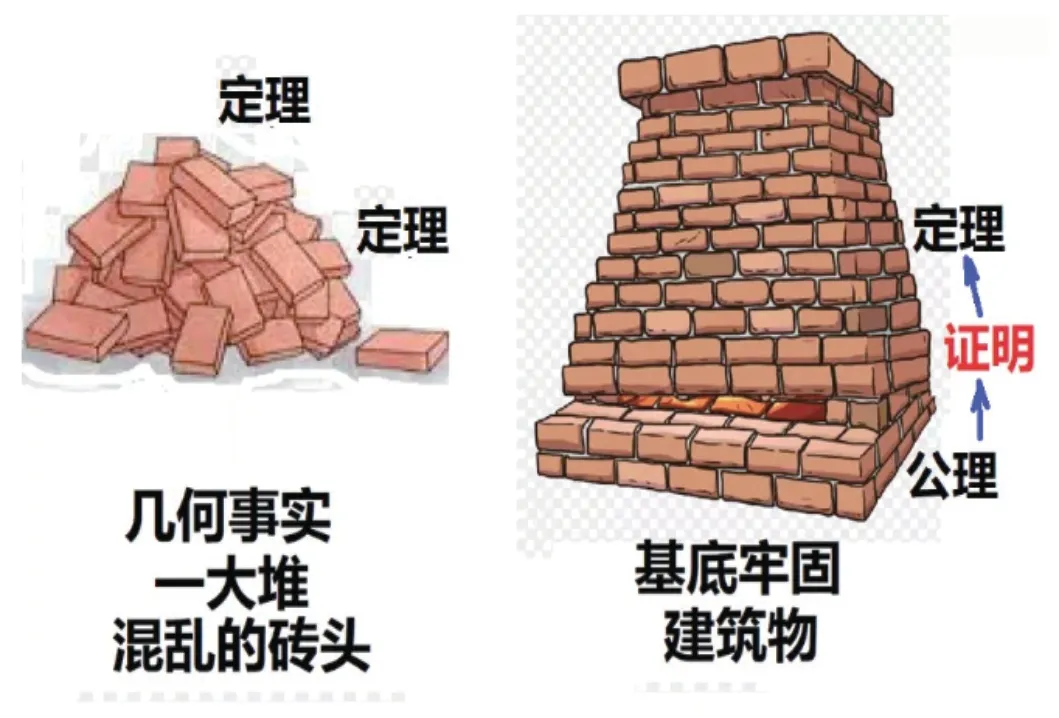
幾何定理為什么需要被“證明”呢？至少有兩個原因：一是通過“證明”才能確認定理的普適性；二是“證明”能夠發掘幾何事實相互之間的關系，發展邏輯推理的方法。打個比方，未經證明的諸多幾何事實，就像是混亂堆在一塊兒的一堆磚頭，而“證明”將它們互相關聯起來，建造成宏偉的建筑物。

其他的文明在更早的時期就發現了很多的幾何事實，都有早期數學知識的記載。但因為不強調形式邏輯，沒有發展出演繹、證明、公理化等方法，因而未成大器。

泰勒斯首開先河的“理性精神”，是數學的精髓。

泰勒斯劃時代的貢獻是引入了“證明”的思想，將數學從經驗上升到理論，這在數學史上是一次不尋常的飛躍，為畢達哥拉斯創立理性數學、歐幾里得的公理化幾何等奠定了基礎。較之世界其他文明，這是古希臘獨有的，使其成為數學乃至科學的奠基者。