竹條粘合箱形壓桿受力性能試驗研究
劉旭,李孟竺,鄭凱旋
(1山地城鎮(zhèn)建設(shè)與新技術(shù)教育部重點試驗室(重慶大學),重慶 400045;2重慶大學 土木工程學院,重慶 400045)
0 引言
2005年,由浙江大學倡導,國內(nèi)11所高校共同發(fā)起全國大學生結(jié)構(gòu)設(shè)計競賽,該競賽成為經(jīng)教育部和財政部批準的全國性學科競賽項目[1-2]。近年來,結(jié)構(gòu)設(shè)計競賽為適應(yīng)社會的發(fā)展,給出的賽題模型多為大跨、高聳、懸挑結(jié)構(gòu),制作出的模型柱子大多細長,學生參賽作品經(jīng)常發(fā)生失穩(wěn)破壞。全國大學生結(jié)構(gòu)設(shè)計競賽近十年才得以大規(guī)模舉辦,對結(jié)構(gòu)模型所用材料的性能研究尚不充分,且大多數(shù)研究集中在竹皮材料性能上,因此可供參考的竹條性能試驗數(shù)據(jù)及結(jié)論較為匱乏,有關(guān)竹條的各種性能還有待開展更充分的研究。
王漢坤[3]研究了不同含水率對竹材順紋抗壓、順紋拉伸、順紋抗剪和彎曲強度的影響,結(jié)果表明,除了順紋抗壓強度隨著含水率的增加呈線性減小,剩下的3個力學指標均呈減小—(增加)—平穩(wěn)—減小的變化趨勢。雷鳴宇等[4]對單層竹皮材料和多層粘接竹皮材料的順紋抗拉強度、抗壓強度、斷裂伸長率等因素展開探究,認為膠水對提高材料強度有所貢獻,竹皮材料斷裂伸長率普遍為0.5%~1.5%,屬于脆性材料。侯應(yīng)貴等[5]研究了竹材不同厚度及刷膠層數(shù)對抗拉承載力的影響,得到了以下結(jié)論:三種不同厚度的竹皮,抗拉強度隨厚度增加而增大,竹條的抗拉強度優(yōu)于竹皮。Lee、Moreira、Mitch等[6-8]對竹材力學性能的測試方法做了詳細總結(jié),包括竹材的徑向抗拉強度和彈性模量測試方法、順紋抗剪模型和方法等。
目前關(guān)于競賽用竹條構(gòu)件的穩(wěn)定性研究尚處于空白,并不能指導構(gòu)件的設(shè)計。為改善以模型破壞試驗尋求最優(yōu)解的現(xiàn)狀,并為參賽者進行箱形截面構(gòu)件截面設(shè)計時提供科學的理論參考,本文開展了竹條粘合箱形壓桿受力性能試驗研究,提出了竹條受壓箱形截面柱的計算公式與整體穩(wěn)定性能的設(shè)計方法。
1 試驗概況
1.1 試件設(shè)計
試驗所用竹條由杭州邦博(BAMBOO)科技有限公司提供,與結(jié)構(gòu)設(shè)計大賽提供材料的供應(yīng)商為同一家。試驗前,對三種規(guī)格(截面分別為6mm×1mm、3mm×3mm、2mm×2mm)竹條實際厚度進行測量,其均差均小于0.05mm,故計算時采用所給標準尺寸。
如圖1,箱形試件由四根6mm×1mm光潔筆直且無竹節(jié)的竹條四面圍合而成,用膠水將其粘接。試件的長細比包括10、20、30、40、50、60、70、80、90和100共10種,每種試件的長度根據(jù)長細比及試件截面的回轉(zhuǎn)半徑確定,每種長度各10根。

圖1 箱形試件
長細比相同的構(gòu)件的穩(wěn)定承載力受構(gòu)件加工質(zhì)量和制作工藝影響較大,而構(gòu)件加工質(zhì)量的好壞主要表現(xiàn)在構(gòu)件的初彎曲大小方面,參考《鋼結(jié)構(gòu)設(shè)計標準》(GB 50017-2017)[9]確定構(gòu)件初彎曲不超過1/1000,經(jīng)測量統(tǒng)計,本研究所制作的構(gòu)件初彎曲均不超過該值。
1.2 材料性能試驗和短柱試驗
單軸抗拉試件制備參照行業(yè)標準《建筑用竹材物理力學性能試驗方法》(JG/T 199-2007)[10]。三種規(guī)格(截面分別為6mm×1mm、3mm×3mm、2mm×2mm)的竹條各制作試件10個,夾持部位分別采用截面6mm×1mm、3mm×3mm、2mm×2mm的竹條進行粘結(jié)保護,其長度為30mm,標距L0=150mm。通過靜力拉伸試驗獲取材料的基本力學性能(包括彈性模量E、抗拉強度fu、極限應(yīng)變εu),試驗結(jié)果的平均值如表1、表2所示。
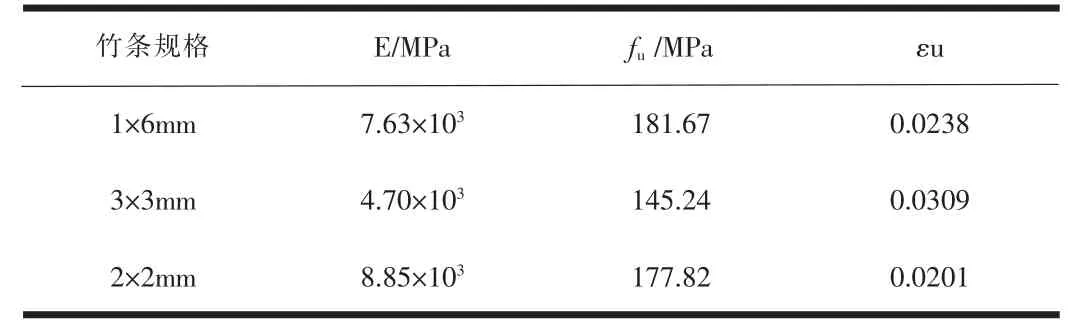
表1 無竹節(jié)竹條試驗結(jié)果
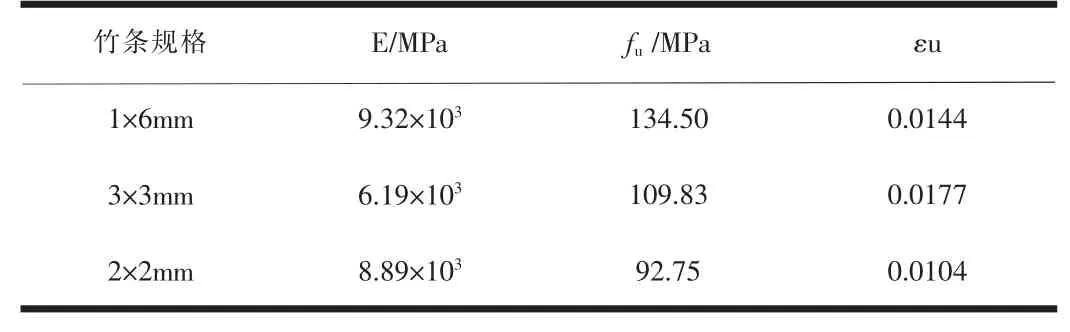
表2 有竹節(jié)竹條試驗結(jié)果
為得到局部失穩(wěn)極限應(yīng)力值,設(shè)計短柱試驗。試件由竹條粘結(jié)而成,并用砂紙打磨為圓柱體。其高度為24mm,橫截面直徑為8mm,共制作試件10個。試驗結(jié)果平均值如表3所示。
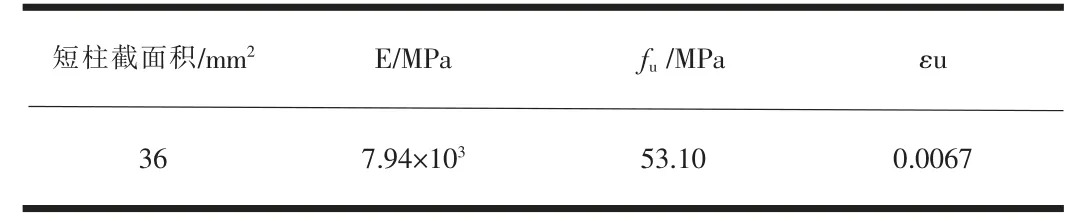
表3 短柱實驗結(jié)果
1.3 試驗裝置及加載制度
試驗采用FBS-5000N微機控制電子萬能試驗機進行豎向加載。試件兩端為剛度遠大于試件的加載圓盤,由于試件端截面較小,圓盤對試件轉(zhuǎn)動約束較小,因此可近似看做兩端鉸接。
測量設(shè)備包括試驗機配套的力傳感器、位移測量系統(tǒng)、變形測量系統(tǒng)、位移計等。位移計為量程為25.4mm的數(shù)顯百分表,布置于試件跨中以測量試件失穩(wěn)平面內(nèi)的水平位移;試驗裝置自帶位移測量系統(tǒng)可直接測量試件的豎向變形,即柱頂端加載點位移。
試驗以1mm/min的速度進行位移加載,試驗機自行采集荷載峰值和位移值,并繪制荷載—位移曲線,當試驗力值下降超過峰值的50%時停止加載。
2 試驗結(jié)果及分析
2.1 極限承載力試驗結(jié)果
對10組不同長細比試件的承載力實驗結(jié)果進行統(tǒng)計,并計算各組桿件承載力的平均值,匯總于下文3.1節(jié)表4。
2.2 試件破壞形式及變形分析
試件典型的失穩(wěn)破壞形態(tài)如圖2所示,可知構(gòu)件在受荷時,同時存在局部穩(wěn)定和整體穩(wěn)定問題。

圖2 試件典型失穩(wěn)破壞形態(tài)
長細比小于臨界長細比的試件以局部失穩(wěn)破壞為主,如圖2a)。加載初期荷載位移曲線呈線性變化,隨著荷載逐漸增大,組成構(gòu)件的板件開始發(fā)生局部屈曲,初始波幅較小,此時已有部分板件退出工作,但構(gòu)件仍具有一定的屈曲后強度;而隨著荷載繼續(xù)增大,板件波幅也繼續(xù)增大,直至試件最終破壞。長細比大于臨界長細比的試件以整體失穩(wěn)破壞為主,如圖2b)。試件在加載過程中持續(xù)彎曲,撓度不斷加大,此時試件在較大的撓度下仍沒有被破壞;而當撓度增加到一定程度時,桿件中點截面在軸力與彎矩作用下,受壓側(cè)板件應(yīng)力達到局部屈曲臨界應(yīng)力,此時,板件開始發(fā)生凹凸,即產(chǎn)生局部屈曲,當達到局部屈曲極限應(yīng)力時,試件被破壞,豎向承載力開始下降。
3 竹條軸壓箱形構(gòu)件整體穩(wěn)定性能設(shè)計方法
3.1 試驗值與規(guī)范值對比
將十組不同長細比的竹條軸壓箱形構(gòu)件試驗所測得的極限承載力(FU)取平均值作為試驗結(jié)果,并將試驗結(jié)果與《木結(jié)構(gòu)設(shè)計標準》(GB 5005-2017)[11]所計算出的極限承載力(Fc)進行對比分析。
在《木結(jié)構(gòu)設(shè)計標準》中,軸心受壓桿件承載力的計算按下式確定:
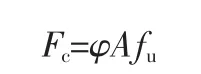
式中:A為構(gòu)件截面凈面積;fu為試件順紋抗壓強度;φ為穩(wěn)定系數(shù)。
其中,構(gòu)件的穩(wěn)定系數(shù)由下式確定:
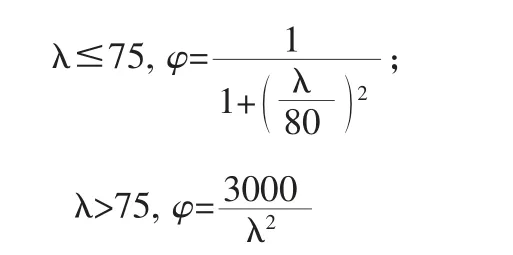
實測值的穩(wěn)定系數(shù)由下式確定:
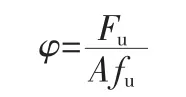
式中:A為構(gòu)件截面凈面積;Fu為構(gòu)件試驗承載力;fu為試件順紋抗壓強度。
將按照《木結(jié)構(gòu)設(shè)計標準》計算得出的受壓承載力Fc及其穩(wěn)定系數(shù)φ1,試驗所得極限承載力Fu及其按照實測值計算所得的穩(wěn)定系數(shù)φ2匯總于表4,其中試件截面凈面積A=24mm2,試件順紋抗壓強度fu由短柱試驗測得,取為53.1MPa。
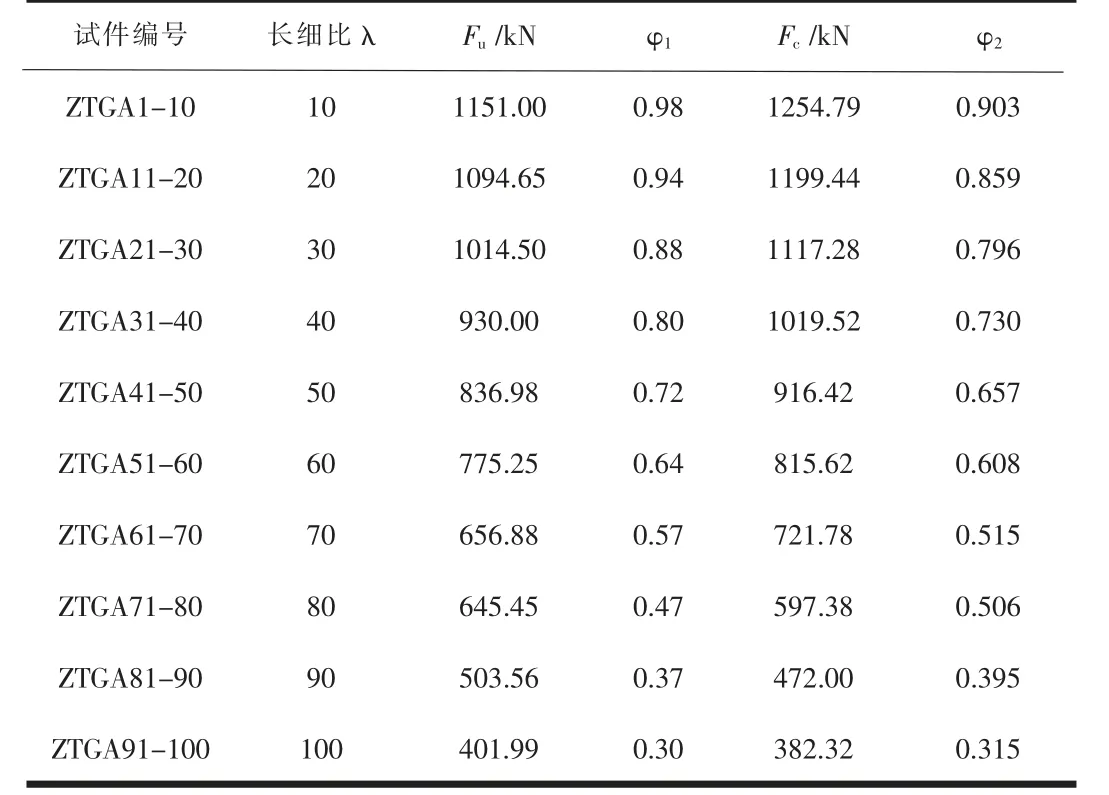
表4 試件承載力與穩(wěn)定系數(shù)
試驗所得的軸心受壓柱的極限承載力與規(guī)范所計算得出的極限承載力的數(shù)據(jù)擬合圖如圖3,兩者對比可得出:當長細比λ≤75時,試驗值明顯小于規(guī)范值,可能是由于手工制作等誤差,或是由于竹木結(jié)構(gòu)的力學性能存在一定的不同;當長細比λ>75時,規(guī)范值與試驗值基本重合,受外界影響因素較小。為得出更為準確的竹條軸壓箱形構(gòu)件極限承載力計算公式,需對規(guī)范中的穩(wěn)定系數(shù)加以修正。
3.2 整體穩(wěn)定系數(shù)與承載力計算公式
將試驗所得的極限承載力計算得出的穩(wěn)定系數(shù)繪于圖4中,并對試驗數(shù)據(jù)進行擬合。
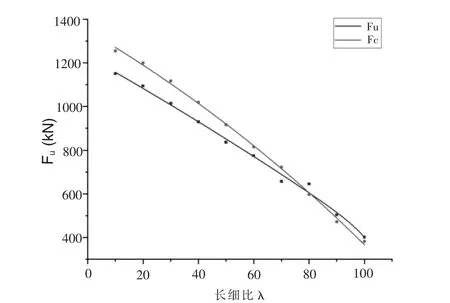
圖3 極限承載力數(shù)據(jù)擬合圖
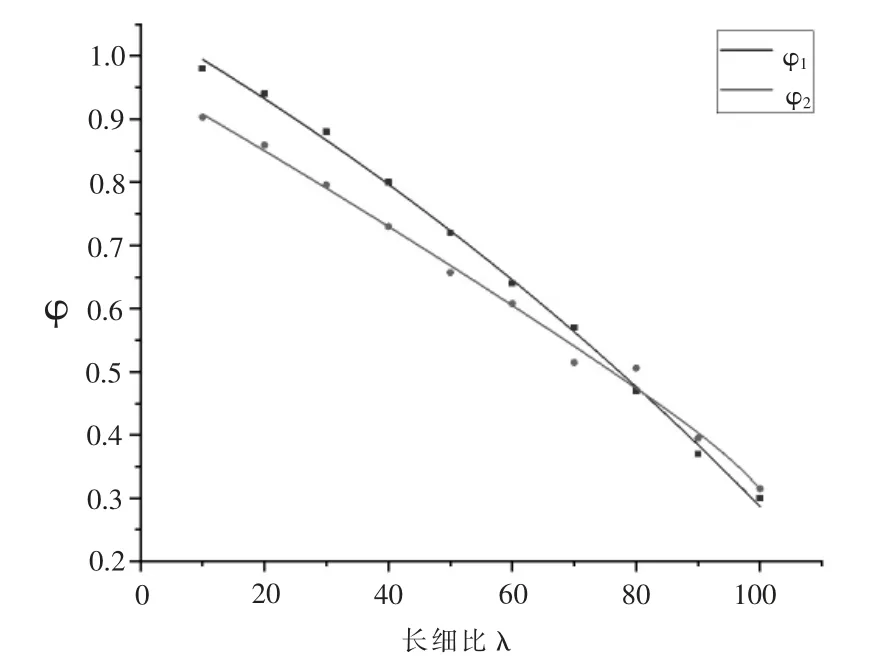
圖4 穩(wěn)定系數(shù)擬合圖
實驗結(jié)果表明:當長細比λ≤75時,《木結(jié)構(gòu)設(shè)計標準》中穩(wěn)定系數(shù)的取值偏大,故對此進行修正;而λ>75時,規(guī)范值與實驗值擬合程度高,仍采用規(guī)范中穩(wěn)定系數(shù)的取值方法。
當長細比λ≤75時,引入修正系數(shù)k。由線性回歸分析可得,φ1與φ2存在一定的線性比例關(guān)系,且故引入修正系數(shù)k=0.9對《木結(jié)構(gòu)設(shè)計標準》中的φ值進行修正。
修正后的竹條粘合箱型桿件軸心受壓情況下的柱子曲線如圖5所示。

圖5 柱子曲線圖
構(gòu)件極限承載力按下式確定:
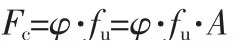
其中,fu=53.1MPa,穩(wěn)定系數(shù)φ按下式確定:
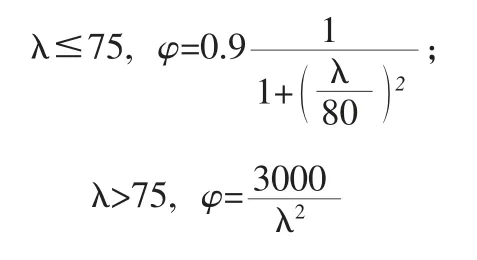
4 結(jié)論
(1)竹條粘合箱形壓桿在受荷時,同時存在局部失穩(wěn)與整體彎曲失穩(wěn)問題。長細比小于臨界長細比的構(gòu)件在受壓時以局部失穩(wěn)為主,長細比大于臨界長細比的構(gòu)件以整體失穩(wěn)為主。目前結(jié)構(gòu)大賽中較為常用的竹條粘合桿件大多為長細桿,主要以整體失穩(wěn)為主。
(2)參考《木結(jié)構(gòu)設(shè)計標準》中關(guān)于軸心受壓桿件承載力計算公式,得出了竹條粘合箱形壓桿常見長細比下的整體穩(wěn)定系數(shù)與承載力計算公式:
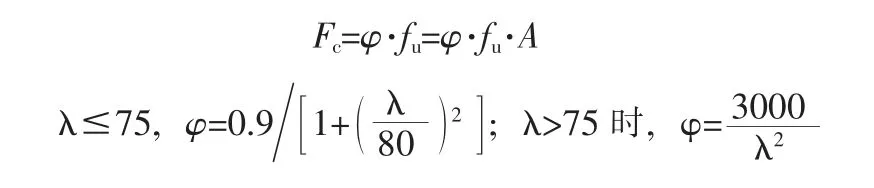
(3)竹條粘合箱形壓桿的穩(wěn)定承載力受材料本身初始缺陷與構(gòu)件制作加工水平的影響。在進行截面設(shè)計時,不能僅套用計算公式,還需對材料缺陷率與制作加工水平進行總體評定并乘以一定的折減系數(shù)保證其準確性。

