基于動態時間規整下密度聚類的軌跡識別研究

吳 達，呂 銳，楊 宇，鄧建軍，張保山，2

（1.空軍工程大學防空反導學院，西安 710051；2.解放軍92095 部隊，福建 臺州 318050）

0 引言

隨著航空發動機、氣動外形設計、飛行控制系統、機載武器系統、空戰指揮系統等不斷更新換代，戰斗機的機動動作也越來越復雜多樣，而目前的目標軌跡生成系統多是根據經驗人為設定的［1-2］，難以保證與真實戰場的貼近性、真實性和準確性，在難以獲得飛行訓練手冊和作戰中，對戰斗機的操縱要求以及飛行員的飛行習慣的情況下，通過演習、模擬訓練等飛行記錄數據獲得的機動動作更加可靠。現今關于機動識別的算法多是運用SVM［3-4］、神經網絡［5-7］、動態貝葉斯網絡［8-9］、HMM［10-11］等算法構建分類器，進行機動類型的分類，或者通過構建機動動作庫［12-13］，通過模板匹配［14-16］的方法進行識別，上述方法得到的結果并不能運用于目標軌跡生成，因為上述方法僅僅得到機動動作的類型，而沒有考慮機動過程中特征參數峰值的差異導致的分類。對于構建分類器的方法來說，需要一部分有參數峰值標簽的數據。對于構建機動動作庫進行模板匹配的方法來說，需要不斷更新新的機動動作和相關經驗知識。

張夏陽［17］考慮對飛行數據進行聚類獲得了11種機動動作類型，方法中用一組均值與方差構成的特征向量表示每個機動片段，僅僅考慮了空間維度的變化，對時間維度上的變化考慮較少。姚佩陽［14］考慮用DTW 距離將樣本與模板軌跡進行匹配，DTW 距離充分考慮了時間維度，但是兩條軌跡進行規整的過程需要較大的計算量，直接對每兩條軌跡計算DTW 距離而后進行聚類的效率是極低的。不妨利用DBSCAN 算法對所有的軌跡點進行預分類，使得被聚為一類可能性較低的機動片段之間不必再進行DTW 距離計算，再利用DBSCAN 改進DTW聚類方法，對可能分為一類的軌跡進行計算，確定其所屬分類。

1 特征及機動片段提取

從演習訓練數據可以得到北天東坐標系航跡的三維坐標數據，以雷達站位坐標原點O，基本面為原點所在地的大地水平面，3 個坐標軸X 軸指向北極，Z 軸與地表垂直指向空中，Y 軸指向北方，與X、Z 構成右手系。

定義1：一個完整的機動過程是從航跡傾角變化率，航跡偏角變化率和切向加速度由恒定為0 到不為0 的時間結點開始，到不為0 到恒定為0 的時間結點為止。

定義2：機動過程中飛行參數的峰值不同，也被劃分為不同的機動類別。

定義3：機動過程中航跡傾角、航跡偏角、速度改變的累計大小不看作機動類別的區分標準。

為了便于進行聚類分析，排除無關因素，不妨采用航跡傾角變化率、航跡偏角變化率和切向加速度（以上這3 種飛行參數統稱為特征參數）作為特征。

1.1 航跡偏角變化率的獲取方法

1.2 航跡傾角變化率的獲取方法

1.3 切向加速度的獲取方法

圖1 軌跡點特征參數空間分布圖

2 基于DBSCAN 改進DTW 機動軌跡分析

2.1 基于DBSCAN 軌跡預分類

DBSCAN 中鄰域半徑和鄰域中核心點的最小數量MinPts 是其關鍵參數，關于DBSCAN 的具體定義可以參考文獻［18］。

在使用DBSCAN 方法進行軌跡預聚類時，需要進行以下適用性改進：在飛行過程中，進行協調轉彎、抬頭機動、切向加速等機動時，會導致發動機需要提供的功率增大［19］。但是發動機的最大輸出功率是有限的，一種特征參數的增加會使另外兩種特征參數最大值減小，產生負相關性，采用加權的歐式距離或對特征參數進行歸一化都不是最適用的。而馬氏距離既獨立于測量尺度，又考慮到各種特性之間的聯系。對于一個均值為μ，協方差矩陣為S 的多變量向量，兩點間的馬氏距離表示為

其中，X 是由所有軌跡點的特征向量構成的矩陣。

n 為最大機動片段數量，mi是第i 個機動片段的最大軌跡點數量。

設定作為核心點鄰點的限制條件，使同一機動片段的點無效，可以避免相同機動片段間較小距離的軌跡點聚為一個點簇。

2.2 構建基于DBSCAN 改進DTW 機動軌跡識別模型

動態時間規整（DTW）是通過計算T 與R 之間的累積最小歐式距離。當兩條軌跡長度相等時，可以通過直接計算T 和R 的距離，距離越小，兩個序列相似度越高。當兩條軌跡長度不相等時，DTW 采用動態規劃（Dynamic Programming，DP）方法來識別。關于DTW 的詳細說明可參考文獻［20］。

早已有相關學者采用DTW 方法對航跡進行聚類或者分類的研究［15］，但很少見到從航跡特征的角度對DTW 方法進行分析：

在戰斗機機動動作中往往存在類似于如下模式的機動過程：以協調轉彎為例，戰斗機往往先是逐漸增加坡度，進入一個較為穩定的轉彎狀態，此狀態下θ 會基本保持不變，累計轉彎角度Δθ 會逐漸增大，然后再逐漸減小坡度改出機動狀態，由定義3 可知，Δθ 的大小不會影響機動類別的劃分，而DTW 方法會自動對θ 值相同的點進行合理對應，使得DTW 距離不會因Δθ 的大小而產生明顯變化。

再者由于記錄的軌跡點之間的時間差不是均等的，且飛行員使用操縱桿的習慣不同，使得擁有相同變化趨勢的軌跡擁有不同的記錄點數量，DTW 方法會自動對變化過程中的處于相似進度的記錄點進行匹配，來減小記錄點數量不同所帶來的影響。

3 實驗分析

實驗1 DBSCAN 改進DTW 聚類算法

實驗1 的數據由專家根據相關經驗知識，在目標軌跡生成軟件上，根據想定參數繪制的10 條完整航跡。包含機動動作詳細情況如下表1 所示。

表1 機動動作設置表

圖2 是其中一條完整的航跡。

圖2 航跡效果圖

表2 DBSCAN 改進DTW 算法分類結果表

其軌跡分類結果如圖3 所示，不同類別的機動片段放于不同區域內，不同機動片段用不同顏色表示，其中，錯誤劃分片段由紅色曲線標出，虛假片段由綠色曲線標出。

圖3 DBSCAN 改進DTW 算法分類結果軌跡圖

實驗結果驗證了DBSCAN 改進DTW 聚類算法對于第1 節所定義的分類規則的適用性，即飛行參數φ、θ、vt的起始值，飛行參數φ、θ、vt的累計變化值以及軌跡段的疏密程度，不會影響DBSCAN 改進DTW 聚類算法對機動類別的劃分，同時，實驗結果中出現的誤識別，也體現出DBSCAN 改進DTW 聚類算法對于特征參數峰值的不敏感性。

實驗2 DBSCAN 預分類的DBSCAN 改進DTW聚類算法

實驗2 的數據與實驗1 中相同。

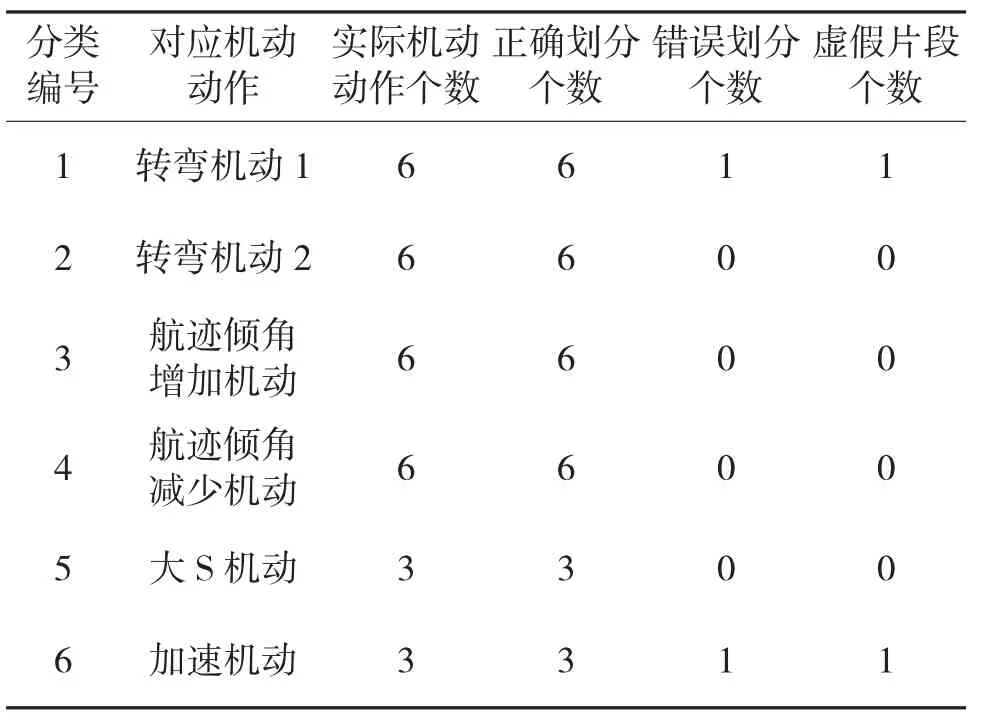
表3 DBSCAN 預分類的DBSCAN改進DTW 算法分類結果表

其軌跡分類圖如圖4，不同類別的機動軌跡段放于不同區域內，不同機動軌跡段用不同顏色表示，其中，虛假片段軌跡已由綠色曲線標出。

圖4 DBSCAN 預分類的DBSCAN 改進DTW 算法分類結果軌跡圖

實驗2 的總運行時間相比于實驗1 減少了16.41 %。主要是由于DBSCAN 預分類限制了DBSCAN 改進DTW 聚類算法進行運算的最大規模，雖然DBSCAN 預分類本身也會加大計算時間的開銷，但相較于由此帶來的計算時間復雜度的減小是十分值得的。

實驗3 數據結構對分類結果的影響

實驗3 中的數據來自模擬訓練的記錄數據。每條航跡中機動片段的機動類型已由記錄數據給出。

表4 數據結構參數設置表

實驗結果如圖5 所示，從圖中曲線的趨勢可以看出，無論是機動軌跡段的總數x，還是機動軌跡段的平均長度n 的增加，都會使DBSCAN 預分類的DBSCAN 改進DTW 聚類算法在時間復雜度上的優化效果更為明顯。同時對比圖5（a）和圖5（b）也可以發現，x 增加帶來的效果更為明顯。圖5（c）說明數據總量的增加也會使錯誤率f（錯誤劃分的機動軌跡段數量占總機動軌跡段數量的比率）增加，但也是在可以接受的范圍內。

圖5 數據結構的影響

實驗4 聚類參數對分類結果的影響

表5 數據結構參數設置表

實驗結果見圖6，圖6（a）中兩種算法在運行時間上的差值隨著c 的增加，有增大的趨勢，說明用于預分類記錄點的數量比例越少，算法優化的效果越明顯。而在c=0.10 時，算法的運行時間均有較大增加，對照圖6（b）中c=0.10 時，錯誤率明顯增加，而正確率（正確劃分的軌跡段的數量與總共軌跡段數量的比率）沒有明顯變化，可知由于數據誤差波動的存在，使得虛假機動軌跡段大量增加。而當c=0.30，時算法運行時間有較大減少的異常現象，對照圖6（b）可知，此時由于門限值選取過大，使得部分機動軌跡段被忽略。

圖6（c）中兩種算法運行時間上的差值隨著d的增加，呈現先保持穩定，后減小的趨勢。隨著d 的增加保持穩定說明，DBSCAN 預分類的能力是有限的，需要DBSCAN 改進DTW 聚類算法進行再分類。而當d 繼續增加時，預分類產生的類別數量逐漸減少，再分類承擔的任務增加，使得算法整體的效率降低。在d=0.010 時，同樣出現兩種算法的運行時間有較大減小的異常現象，對照圖6（d）可知，由于半徑參數選取過小，很多機動軌跡段被誤識別為噪聲點。在圖6（d）中隨著d 不斷增加，正確率有先緩慢增加，后基本穩定不變的趨勢。可見，在d 值的一定范圍內，d 越大，越能減少機動軌跡段被誤識別為噪聲點的現象。

圖6 聚類參數的影響

4 結論

通過實驗驗證了DBSCAN 改進DTW 聚類算法對機動軌跡聚類的有效性，并且驗證了DTW 距離度量方法，可以有效屏蔽與預設分類方法無關的影響因素，提高了類別劃分的準確性。通過實驗研究發現，相較于DBSCAN 改進DTW 聚類算法，DBSCAN 預分類的DBSCAN 改進DTW 聚類算法，不僅節省了計算時間上的支出，還可以得到更為精確的類別劃分效果。當數據規模逐漸增大時，DBSCAN預分類的DBSCAN 改進DTW 聚類算法起到的優化效果更為明顯。當其參數取到c=0.20，d=0.020 時，既可以保證較高的正確率，也可以保證算法較高運行效率，此時，DBSCAN 預分類的作用發揮到最大。同時要注意，若參數選取不當，會造成機動軌跡段的大量丟失或大量虛假片段出現的問題。