運用DGS軟件設計函數圖象變換的教學課件

函數是中學數學核心概念，也是比較難理解的概念。如何更好地設計課件凸顯函數的性質，特別是函數的單調性和奇偶性？筆者以二次函數為例說明如何幫助學生理解函數的圖象變換。

一、函數性質的呈現

（一）函數的單調性

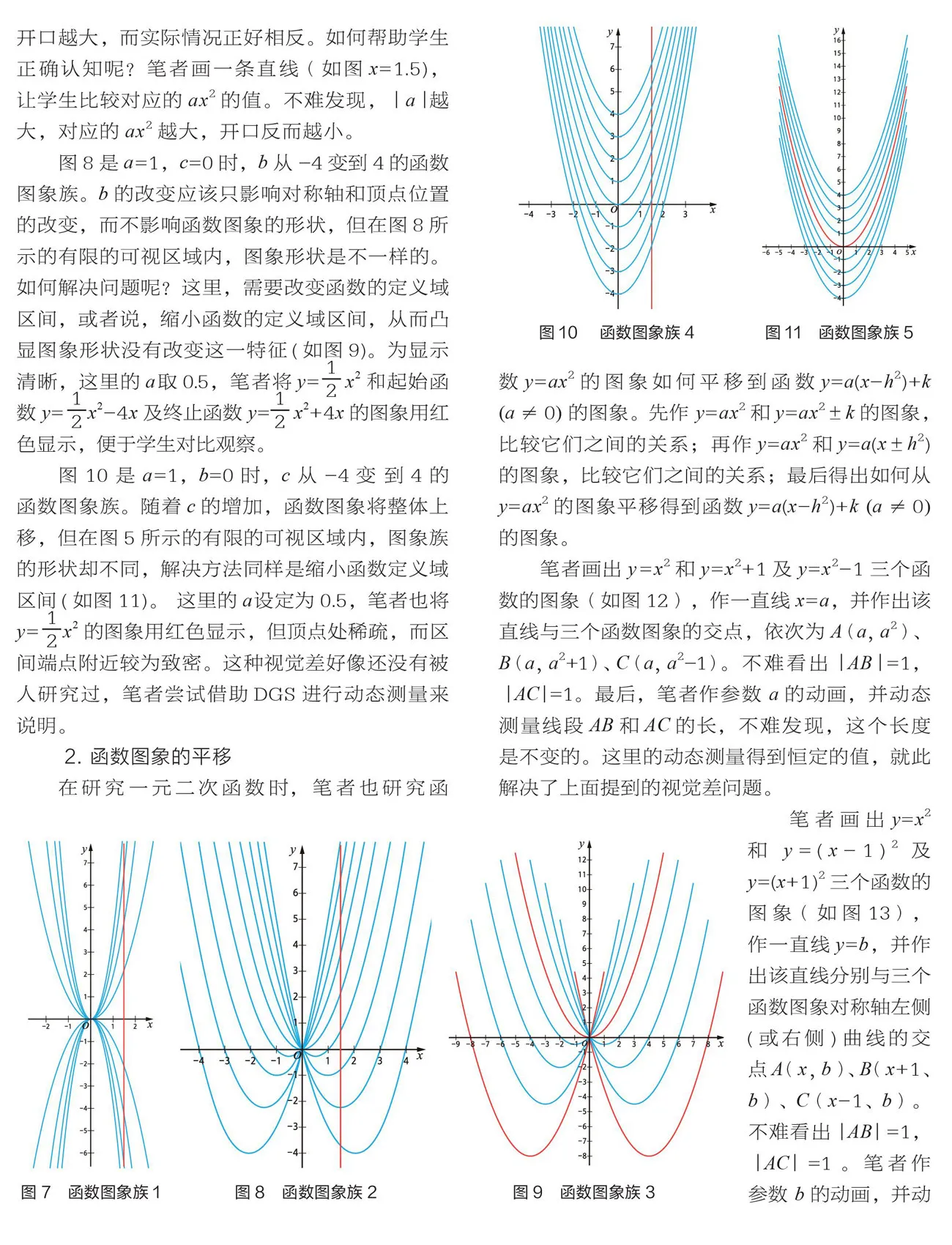
函數的單調性是函數最重要的性質，涉及兩個變量之間的協變關系。單調性在初中教材和高中教材有著完全不同的表述，初中是隨的增大而增大（或減小），而高中則是對單調區間內任意兩點之間函數值的大小作比較來定義的。在初中階段，如果不引導學生如何看圖，學生很難理解單調性的意義。例如，教學正比例函數= 的單調性時，筆者運用動態幾何軟件（Dynamic Geometry Software，簡寫為DGS）中，按如下過程作圖（如圖1）：

（1）作函數= 的圖象，圖形區域可顯示的的范圍由可見的的范圍和的范圍確定。

（2）作兩個點（，0）和（， ），再作連接它們的線段，并跟蹤該線段。

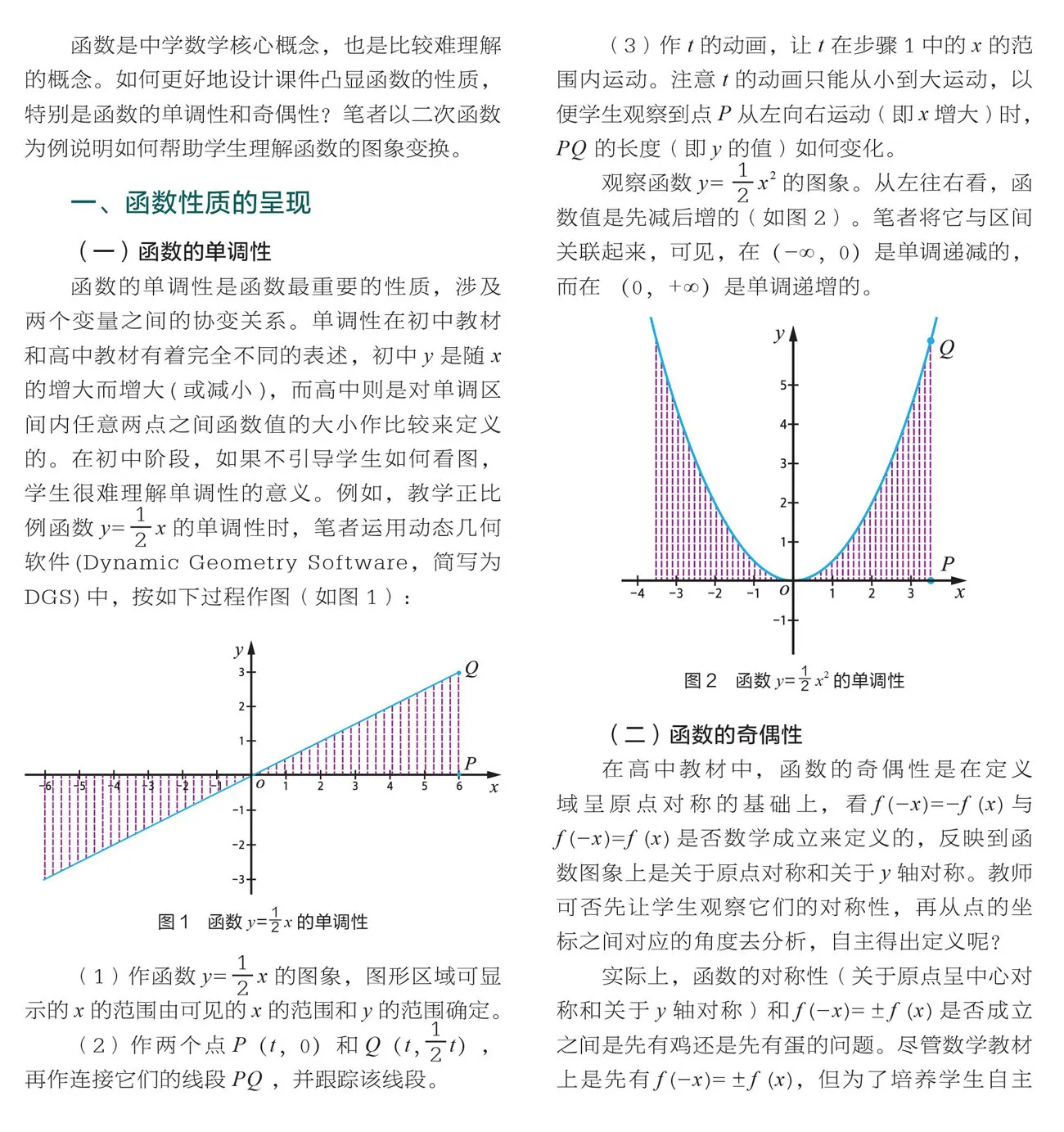
（3）作的動畫，讓在步驟1中的的范圍內運動。注意的動畫只能從小到大運動，以便學生觀察到點從左向右運動（即增大）時，的長度（即的值）如何變化。

觀察函數= ²的圖象。從左往右看，函數值是先減后增的（如圖2）。筆者將它與區間關聯起來，可見，在（-，0）是單調遞減的，而在（0，）是單調遞增的。

（二）函數的奇偶性

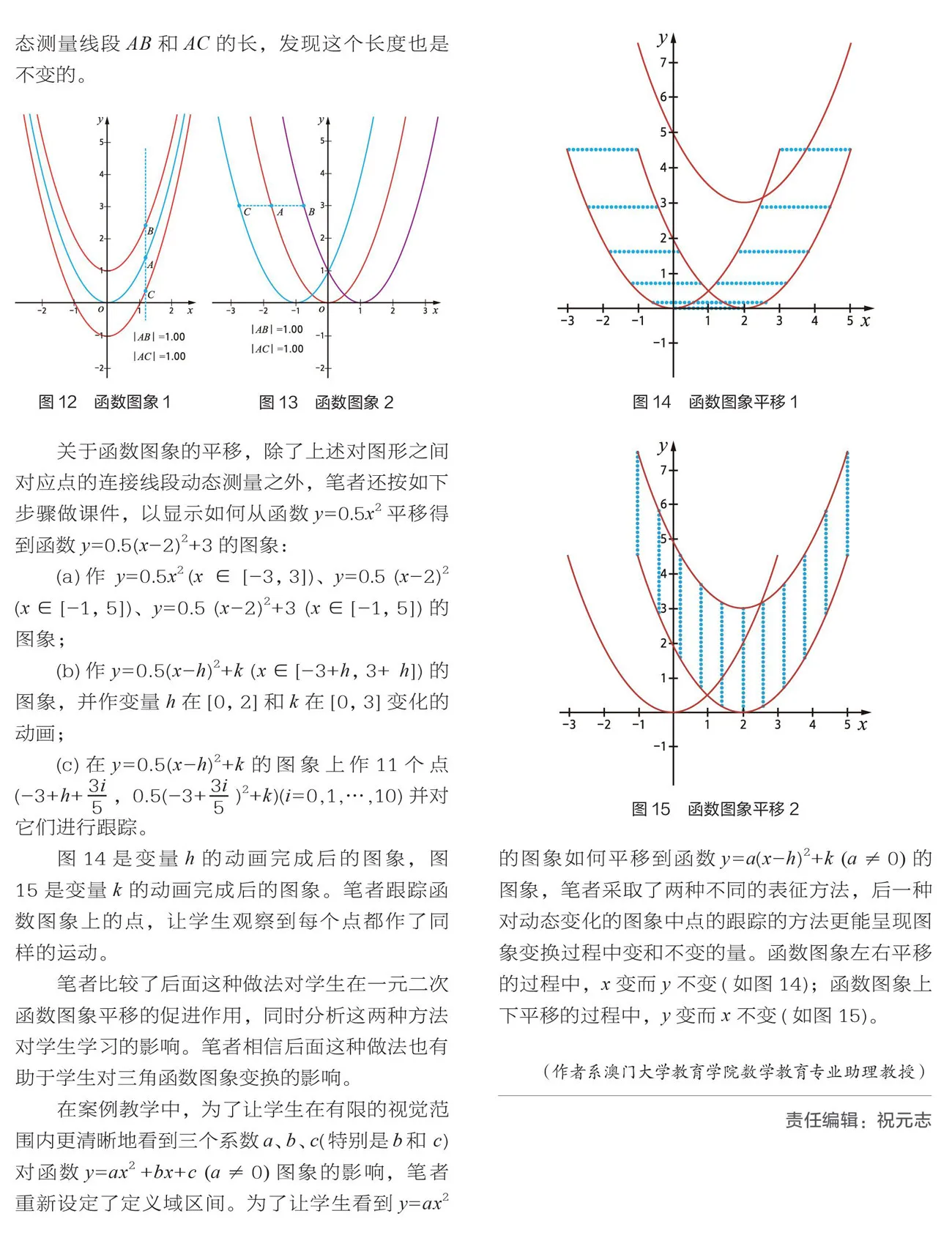
在高中教材中，函數的奇偶性是在定義域呈原點對稱的基礎上，看 （-）=- （）與 （-）= （）是否數學成立來定義的，反映到函數圖象上是關于原點對稱和關于軸對稱。教師可否先讓學生觀察它們的對稱性，再從點的坐標之間對應的角度去分析，自主得出定義呢？

實際上，函數的對稱性（關于原點呈中心對稱和關于軸對稱）和 （-）=± （）是否成立之間是先有雞還是先有蛋的問題。盡管數學教材上是先有 （-）=± （），但為了培養學生自主探究數學概念并給出定義的能力和對圖形特點的分析能力，筆者讓學生從圖象入手來理解而不是“照本宣科”。

筆者以= 和= ²為例具體說明（如圖3和圖4）。對函數= ，筆者讓學生先觀察該函數的圖象的對稱性，接著用點與點之間的一一對應關系來解釋。作圖順序：先作（，），再作（-，- ），看著兩點是否關于原點對稱，最后作的動畫。這樣做的目的是便于學生觀察到無論點在何處，其關于原點的對稱點都在該函數的圖象上。偶函數= ²的作圖操作類似。

探究函數的對稱性（如一元二次函數的對稱性）時，師生可以仿照上面作圖。如何演示函數的有界性？筆者在最小值和最大值之間作平行于軸的直線族，讓學生看到最高點和最低點。

二、函數的圖象變換

（一）函數的多重表征

數學中，常常同時用多重表征表示同一個數學概念，如函數常用解析式、表格、圖象等來表示。與只通過單一表征（多數是代數符號表征）學習數學的學生相比，學生通過多重表征學習數學通常對知識的記憶更長久，對知識的運用也更加高效。多重表征可以促進學生對抽象的數學概念的理解。中國的中學數學課程非常強調數形結合方法的使用，引導學生建立代數表征與圖形表征之間的關聯。數形結合方法被廣泛用于數學教學和解決數學問題方面。華羅庚先生曾對數與形之間的關系有段精辟的論述：數缺形時少直觀，形少數時難入微。數形結合百般好，隔離分家萬事休。

多重表征的使用為抽象數學概念的學習提供了便利，然而不同表征之間的變換對學生來說，有時會造成認知障礙。借助現代科技，教師可以幫助學生克服這些認知障礙。德雷福斯指出以多重表征為基礎的歸納過程一般需要經歷如下四個階段：使用單個表征;平行地使用多重表征;在平行的多重表征之間建立聯系;將不同表征整合在一起并能在彼此之間靈活轉換。

一個函數可以用多種表示形式，如語言、數字、圖象和數學符號等形式，它們表示了函數的不同方面。學生完整描述一個函數，不僅需要運用多重表征表示函數，而且需要建立不同表征之間的聯系。大量研究表明，多重表征的運用有助于函數教學。多重表征有助于學生理解觀察到的現象與函數概念之間的聯系，也有助于學生對函數概念的理解，實現從“操作—過程—對象—圖示”理論中的操作水平到過程水平的提升。

代數表征和圖象表征之間的互動可以幫助學生在大腦中建構關于函數圖象變換（包括平移）的知識。下面，筆者以動態幾何軟件（Dynamic Geometry Software，簡寫為DGS）為媒介說明如何幫助建立函數多重表征之間的聯系。在函數圖象變換的過程中，DGS可以動態地呈現原圖象上的點如何移到新得到的函數圖象上，這種動態表征有助于建立原函數圖象和新函數圖象之間的聯系。以DGS為媒介的多重表征有助于學生通過同時顯示的代數表征和圖象表征的變化，歸納函數圖象變換的普遍規律。

（二）兩個認知沖突

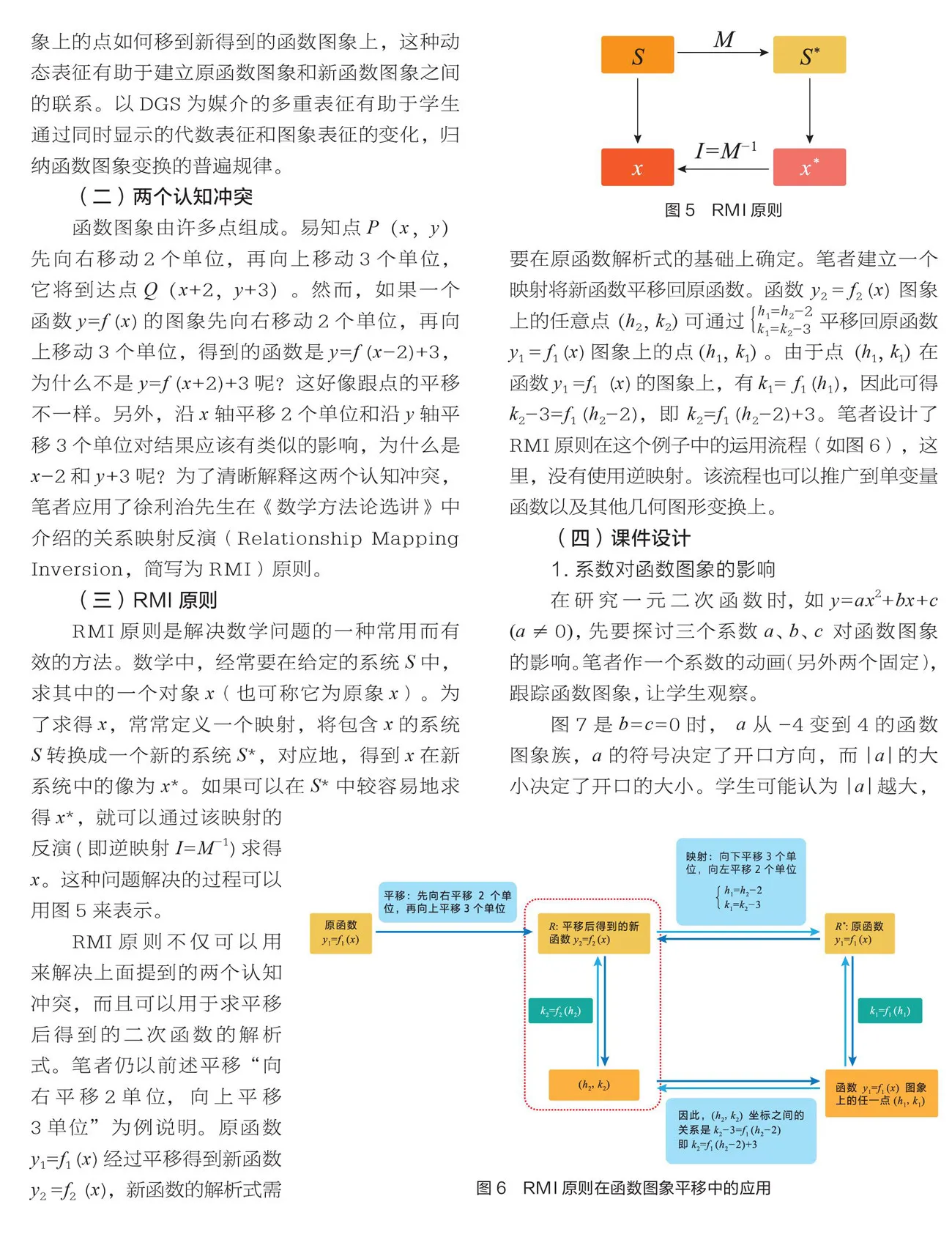
函數圖象由許多點組成。易知點（，）先向右移動2個單位，再向上移動3個單位，它將到達點（+2，+3）。然而，如果一個函數= （）的圖象先向右移動2個單位，再向上移動3個單位，得到的函數是= （-2）+3，為什么不是= （+2）+3呢？這好像跟點的平移不一樣。另外，沿軸平移2個單位和沿軸平移3個單位對結果應該有類似的影響，為什么是-2和+3呢？為了清晰解釋這兩個認知沖突，筆者應用了徐利治先生在《數學方法論選講》中介紹的關系映射反演（Relationship Mapping Inversion，簡寫為RMI）原則。

（三）RMI原則

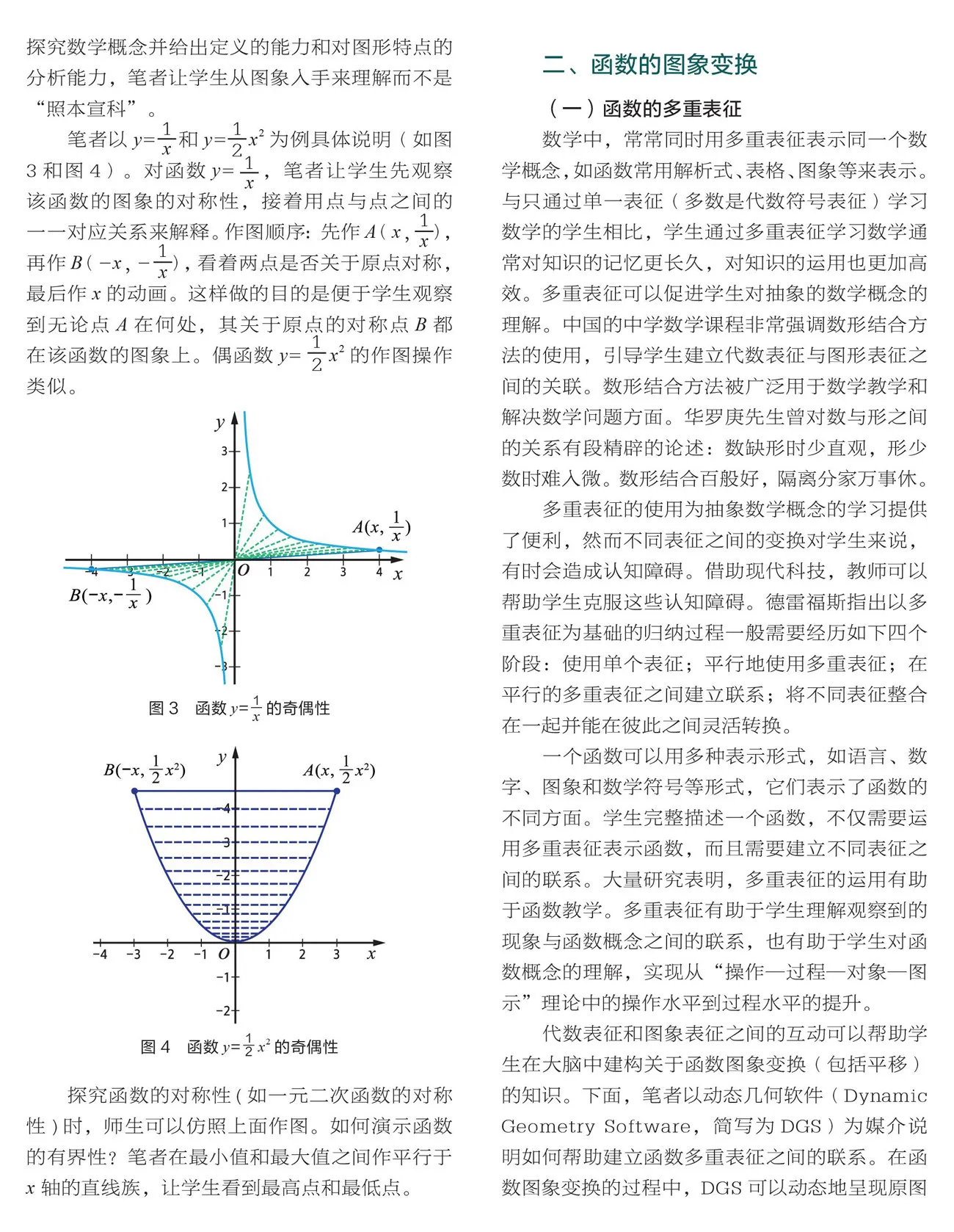
RMI原則是解決數學問題的一種常用而有效的方法。數學中，經常要在給定的系統中，求其中的一個對象（也可稱它為原象）。為了求得，常常定義一個映射，將包含的系統轉換成一個新的系統*，對應地，得到在新系統中的像為*。如果可以在*中較容易地求得*，就可以通過該映射的反演（即逆映射=^-1）求得。這種問題解決的過程可以用圖5來表示。

RMI原則不僅可以用來解決上面提到的兩個認知沖突，而且可以用于求平移后得到的二次函數的解析式。筆者仍以前述平移“向右平移2單位，向上平移3單位”為例說明。原函數= （）經過平移得到新函數= （），新函數的解析式需要在原函數解析式的基礎上確定。筆者建立一個映射將新函數平移回原函數。函數= （） 圖象上的任意點 （，）可通過 平移回原函數= （）圖象上的點（，）。由于點（，）在函數= （）的圖象上，有= （），因此可得-3= （-2），即= （-2）+3。筆者設計了RMI原則在這個例子中的運用流程（如圖6），這里，沒有使用逆映射。該流程也可以推廣到單變量函數以及其他幾何圖形變換上。

（四）課件設計

1.系數對函數圖象的影響

在研究一元二次函數時，如=²++（≠0），先要探討三個系數、、對函數圖象的影響。筆者作一個系數的動畫（另外兩個固定），跟蹤函數圖象，讓學生觀察。

圖7是==0時，從-4變到4的函數圖象族，的符號決定了開口方向，而丨丨的大小決定了開口的大小。學生可能認為丨丨越大，開口越大，而實際情況正好相反。如何幫助學生正確認知呢？筆者畫一條直線（如圖=1.5），讓學生比較對應的²的值。不難發現，丨丨越大，對應的²越大，開口反而越小。

圖8是 =1，=0時，從-4變到4的函數圖象族。的改變應該只影響對稱軸和頂點位置的改變，而不影響函數圖象的形狀，但在圖8所示的有限的可視區域內，圖象形狀是不一樣的。如何解決問題呢？這里，需要改變函數的定義域區間，或者說，縮小函數的定義域區間，從而凸顯圖象形狀沒有改變這一特征（如圖9）。為顯示清晰，這里的取0.5，筆者將= ²和起始函數= ²-4及終止函數= ²+4的圖象用紅色顯示，便于學生對比觀察。

圖10是 =1，=0時，從-4變到4的函數圖象族。隨著的增加，函數圖象將整體上移，但在圖5所示的有限的可視區域內，圖象族的形狀卻不同，解決方法同樣是縮小函數定義域區間（如圖11）。這里的設定為0.5，筆者也將= ²的圖象用紅色顯示，但頂點處稀疏，而區間端點附近較為致密。這種視覺差好像還沒有被人研究過，筆者嘗試借助DGS進行動態測量來說明。

2. 函數圖象的平移

在研究一元二次函數時，筆者也研究函數=²的圖象如何平移到函數=（-²）+（≠0）的圖象。先作=²和=²±的圖象，比較它們之間的關系;再作=²和=（±²）的圖象，比較它們之間的關系;最后得出如何從=²的圖象平移得到函數=（-²）+（≠0）的圖象。

筆者畫出 =²和=²+1及=²-1三個函數的圖象（如圖12），作一直線=，并作出該直線與三個函數圖象的交點，依次為（，²）、（，²+1）、（，²-1）。不難看出丨 丨 =1，丨丨=1。最后，筆者作參數的動畫，并動態測量線段和的長，不難發現，這個長度是不變的。這里的動態測量得到恒定的值，就此解決了上面提到的視覺差問題。

筆者畫出=²和=（-1）²及=（+1）²三個函數的圖象（如圖13），作一直線=，并作出該直線分別與三個函數圖象對稱軸左側（或右側）曲線的交點（，）、（+1、）、（-1、）。不難看出丨丨=1，丨丨=1。筆者作參數的動畫，并動態測量線段和的長，發現這個長度也是不變的。

關于函數圖象的平移，除了上述對圖形之間對應點的連接線段動態測量之外，筆者還按如下步驟做課件，以顯示如何從函數=0.5²平移得到函數=0.5 （-2）²+3的圖象：

（a） 作=0.5² （∈[-3，3]）、=0.5 （-2）² （∈[-1，5]）、=0.5 （-2）²+3 （∈[-1，5]）的圖象;

（b） 作=0.5（-）²+（∈[-3+，3+ ]）的圖象，并作變量在[0，2]和在[0，3]變化的動畫;

（c） 在=0.5（-）²+的圖象上作11個點（-3++ ，0.5（-3+ ）²+）（=0，1，…，10）并對它們進行跟蹤。

圖14是變量的動畫完成后的圖象，圖15是變量的動畫完成后的圖象。筆者跟蹤函數圖象上的點，讓學生觀察到每個點都作了同樣的運動。

筆者比較了后面這種做法對學生在一元二次函數圖象平移的促進作用，同時分析這兩種方法對學生學習的影響。筆者相信后面這種做法也有助于學生對三角函數圖象變換的影響。

在案例教學中，為了讓學生在有限的視覺范圍內更清晰地看到三個系數、、（特別是和）對函數=² ++（≠0）圖象的影響，筆者重新設定了定義域區間。為了讓學生看到=²的圖象如何平移到函數=（-）²+（≠0）的圖象，筆者采取了兩種不同的表征方法，后一種對動態變化的圖象中點的跟蹤的方法更能呈現圖象變換過程中變和不變的量。函數圖象左右平移的過程中，變而不變（如圖14）;函數圖象上下平移的過程中，變而不變（如圖15）。

（作者系澳門大學教育學院數學教育專業助理教授）

責任編輯：祝元志