仿真程序在初中數學中的應用

當今，信息技術已經融入人們生活學習的方方面面。《義務教育數學課程標準（2011年版）》明確指出：要充分考慮信息技術對數學學習內容和方式的影響，開發并向學生提供豐富的學習資源，把現代信息技術作為學生學習數學和解決問題的有力工具，有效地改進教與學的方式，使學生樂意并有可能投入到現實的、探索性的數學活動中去^[1]。如何有效借助信息技術，使之更好地與初中數學教學相結合呢？ 一直以來，二次函數是初中教學的重點和難點，學生學習和理解有一定困難。筆者以PhET互動式仿真程序為載體，探討二次函數的圖象和性質，進一步滲透數形結合思想，激發與增強學生學習數學的興趣與信心。

一、關于仿真程序PhET

PhET是Physics Education Technology的縮寫，譯為物理教育技術。諾貝爾物理學獎獲得者卡爾·威曼于2002年發起PhET物理教育科技計劃，并在科羅拉多大學進行研發與試驗，幫助學生更好地了解科學，提升學生的科學素養。隨著計劃的不斷推進以及越來越多教育工作者的參與，適用于化學、生物學、地理及數學等學科的互動仿真程序開始出現，PhET已超出最初的構想，但是為了維持名稱的一致性，并沒有因學科不同而改名^[2]。卡爾·威曼研究了PhET仿真程序教學，強調仿真程序的特別之處在于“它可以模糊講課、作業、課堂活動、實驗之間的界限。其原因在于一個仿真程序可以通過類似途徑應用于以上所有的教學活動中……同時仿真程序在教師和學生之間提供了一個同等的形象化，這種形象化可以促進交流與教學”^[3]。

PhET仿真互動程序網頁版界面匯集了非常豐富的教學資源。目前，PhET的應用覆蓋小學、中學和大學學段，涉及物理、化學、數學、生物學和地球科學五大學科^[4]。以數學學科的仿真程序為例，主要分為數學概念和數學應用兩大部分，數學概念部分的程序涉及整數、分數、三角函數和向量等內容。數學應用不局限于數學學科，與物理學科也有交叉融合，如電線的電阻、斜拋運動等知識。PhET的界面簡潔，其中的仿真程序也比較有趣，適于探究。教師應用PhET可以寓教于樂。

二、交互式仿真教學案例分析

二次函數是人教版數學教材九年級上冊第二十二章的教學內容，這部分是初中板塊的重難點。目前，國內將PhET與數學教學相結合的案例較少，更談不上廣泛應用。

在二次函數的新授課環節，教師一般引導學生從一些生活實例出發，比如觀察籃球運動軌跡，抽象出二次函數的數學模型，得出二次函數的定義和一般表達式。然后，引導學生從最簡單的形式=²開始，應用五點作圖法，探究系數與函數圖象的關系。接著，引導學生得出圖象向上、向下、向左、向右平移的表達式。學生掌握平移比較難，需要花費大量時間。由于這一章節的知識體系龐雜，學生學習完之后，不能很好地將各部分知識整合在一起。在復習課環節，筆者借助PhET仿真程序，組織數學活動，讓學生動手驗證新授課上獲得的結論，加深認知與理解，總結形成知識框架。對于二次函數圖象部分，開展了以下四次數學活動。

（一）探索

使用者進入PhET網頁版后，選擇仿真程序中的數學，點擊進入二次函數圖象界面，即可具體操作。筆者選擇探索部分。探索部分設置了表達式=²++，同時還單獨給出了相應的二次項、一次項和常數項（如圖1）。筆者移動滑動方塊，在一定范圍內任意改變二次項、一次項的系數和常數項，讓學生更好地認識各個部分的系數與二次函數圖象的關系。

1.僅改變二次項系數

顯而易見，二次項系數與函數圖象形狀、開口大小、方向有關。二次項系數的絕對值越大，圖象開口越小;二次項系數的絕對值越小，圖象開口越大。當二次項系數>0時，圖象開口方向向上;當二次項系數<0時，圖象開口方向向下;當二次項系數=0時，圖象不再是拋物線，變成一條直線。由此，讓學生加深對二次項系數不能為0的理解。

2.僅改變一次項系數

觀察可知，一次項系數和函數圖象的開口大小和方向都無關，圖象向左或者向右移動，但不是平移。

3.僅改變常數項

觀察可知，常數項和函數圖象的開口大小和方向都無關，圖象向上或向下平移。

通過探索，學生知曉二次函數圖象與系數、和的關系。為什么二次函數圖象的形狀、方向、大小由二次項系數唯一確定，與、無關，而位置卻由、、共同確定呢？筆者將二次函數的表達式=²++進行配方，得： 。它的圖象是由=²的圖象經平移得到，平移不會改變形狀、開口大小和方向，所以二次函數圖象的形狀、大小、方向由二次項系數唯一確定。從配方后的形式也可以看出，圖象的對稱軸為=- ，頂點坐標為（- ， ），所以圖象位置由、和共同確定。

（二）推究標準式

仿真程序中，標準式部分設置了表達式=²++，同時還單獨給出了相應的頂點、對稱軸、根、等式和坐標（如圖2）。筆者將教學重點放在根，即總結二次函數和二元一次方程的關系。通過前面的學習，學生知曉二次函數的圖象=²++與軸的位置關系有三種：沒有公共點;有一個公共點;有兩個公共點。這三種關系分別代表一元二次方程²++=0的根的三種情況：沒有實數根;有兩個相等的實數根;有兩個不等的實數根。通過改變系數，學生可以驗證結論。同時，學生也可以將二次函數和不等式聯系起來，探究當=²++>0和=²++<0時，相應的的范圍。

（三）探究頂點式

在二次函數的標準式中，學生能由的正負判斷出函數圖象開口方向。在頂點式=（-）² +中，學生不僅可以清楚判斷函數圖象的開口方向，而且能直觀得出圖象的對稱軸=和頂點坐標（，）。此外，在含有頂點的區域中，學生可以快速求出函數的最大值或最小值。筆者通過配方將標準式化為頂點式，其中=- ，= ，而將頂點式化標準式則去括號合并同類項即可。

在這部分，筆者引導學生探討=²、=²+和=（-）²圖象的關系（如圖3）。對于圖象向上向下平移，學生掌握較為扎實;對于向左向右平移，則經常將正、負號搞混淆，掌握不扎實。筆者借助PhET，說明“上加下減”和“左加右減”。

1.僅改變系數

觀察可知，僅改變系數，圖象的開口大小、方向和對稱軸均不發生改變。當增大個單位長度時，圖象整體向上平移個單位長度;當減小個單位長度時，圖象整體向下平移個單位長度。

2.僅改變系數

觀察可知，僅改變系數，圖象的開口大小、方向和頂點的縱坐標均不發生改變。當增大個單位長度時，圖象整體向右平移個單位長度;當減小個單位長度時，圖象整體向左平移個單位長度。

筆者借助PhET仿真互動程序，讓學生更加生動直觀地看到平移的情況，加深對函數圖象平移的理解。

（四）探究焦點和準線

仿真程序中，焦點和準線部分設置了表達式 ，同時還單獨給出了相應的頂點、焦點、準線和拋物線上的點。筆者組織相關活動是讓學生簡單了解拋物線的焦點和準線。筆者提問“拋物線上的點到焦點的距離和到準線的距離有什么關系”引發學生思考，為后續他們在高中階段進一步學習拋物線作鋪墊。

三、總結

（一）優點

1.有利于提高學生學習探究的主動性

PhET仿真程序網頁版的界面設計簡潔明了。只要教師稍加指導，學生便能進行相應的操作。這有利于激發和增強學生探究的興趣和信心。系數可以在一定范圍內隨意變化，比單獨的五點法作圖得結論更加便捷。相比較傳統的教學模式，PhET有其特有的優點：學生除了課堂的活動探究外，課下或者課外也可以操作，應用生動直觀化的互動仿真程序，進一步提高學習的積極性和探究的主動性。

2.有利于多維度理解知識的本質

傳統模式下，教師講授二次函數時偏向于抽象化教學，比如從實際問題提出二次函數的模型，讓學生用五點法畫圖，這樣教學可以促進學生從抽象思維的角度掌握知識，理解知識。借助PhET互動仿真程序，教師還可以從直觀思維的角度入手，進行可視化教學，將抽象思維和直觀思維相結合，促進學生多維度理解知識的本質。

3.有利于多種數學思想與方法的滲透

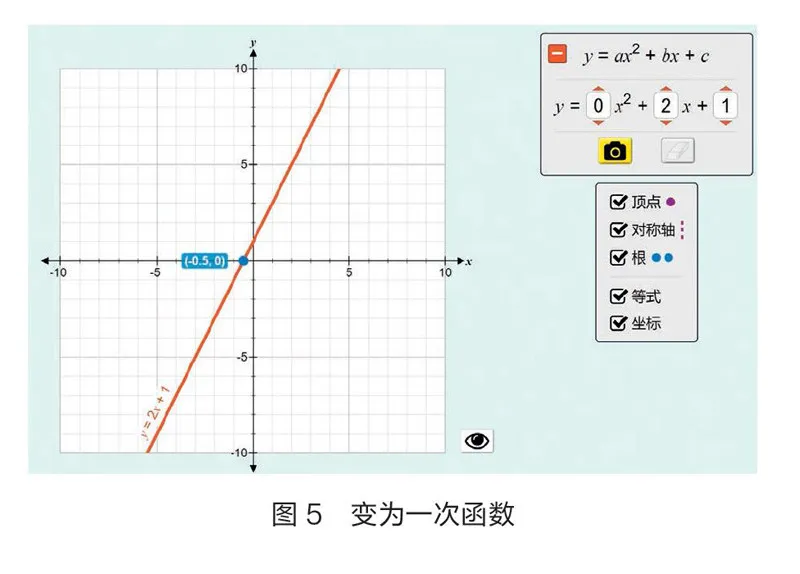
二次函數包含很多重要思想，如數形結合思想、建模思想、函數思想、化歸思想、分類討論思想等。函數有兩個典型特征：一是解析式;二是圖象。從解析式出發，可以進行代數推理;從圖象特征出發，可以研究數與形的結合。學生通過二次函數的學習，借助PhET互動仿真程序，可以更好地掌握數形結合思想^[4]。令二次項系數為0，圖象變為一次函數（如圖5），學生可以進行一次函數和二次函數圖象的對比學習，體會類比思想。再如，探討一元二次方程²++=0的根的三種情況，就體現了分類討論的思想。

（二）局限

1.更適合自主能力強的學生

PhET互動仿真程序的應用不可避免地存在一定的局限性。例如，在教學中，給學生10分鐘自行探究，部分學生可能不知道應該做什么，無所事事。互動仿真程序更適合那些自主學習能力較強，具有較好的自我計劃、自我監控能力的學生^[5]。很多學生學不好，不是因為知識難，而是因為不知道如何學。不知道如何學是教學的難點，這對教師是一個考驗。

2.PhET界面內容有待進一步完善

二次函數的表達式常見的有三種形式：一般式、頂點式和交點式。PhET互動仿真程序的二次函數圖象涉及一般式、頂點式和焦點準線式，但是沒有涉及交點式。筆者認為PhET網頁版還可補充二次函數交點式并加以延伸拓展，供學有余力的學生鉆研。交點式的形式為=（-）（-），其中不等于0，僅圖象與軸有交點時滿足。交點式由韋達定理和一般式聯立得到。

初中處于小學和高中銜接過渡的學段，除了知識的傳授外，教師還要注意培養學生的探究和創新能力，提高他們學習數學的興趣和信心。PhET互動仿真程序作為一種信息技術工具與資源，為信息技術與數學教學融合提供了平臺。筆者以“二次函數圖象”為例，借助信息技術，引導學生全面復習總結了二次函數的圖象和性質。筆者認為，該部分的教學應以傳統方式為主，以信息化方式為輔，相輔相成，提高教學效果。

參考文獻

[1] 中華人民共和國教育部.義務教育數學課程標準：2011年版[S].北京：北京師范大學出版社，2012.

[2] 陳江濤.互動學習工具PhET的發展進程分析與本地化改造[J].軟件導刊，2014，13（4）：196-198.

[3] Wieman C E， Adams W K， Loeblein P，et al. Teaching Physics Using PhET Simulations[J]. The Physics Teacher，2010，48（4）：225.

[4] 王慧.抓住關鍵點 探究新方法——二次函數圖象與性質學習要點[J].基礎教育論壇（下旬刊），2020（1）：60-62.

[5] 楊婉秋，李淑文.美國信息技術與中學數學課堂教學“深度融合”的實踐探索——以PhET數學互動仿真程序的研發與應用為例[J].外國中小學教育，2019（8）：69-70.

（作者劉翠系蘇州大學數學科學學院研究生;程廣文系泰州學院教育科學學院院長，教授）

責任編輯：祝元志