基于二元非線性擬合的溢洪道寬頂堰流量系數公式研究及應用

閆志方，賈云飛，王 宇

(1.廣東珠榮工程設計有限公司，廣東 廣州 510610；2.廣州開發區財政投資建設項目管理中心，廣東 廣州 510000；3.南京水利科學研究院水文水資源與水利工程科學國家重點實驗室，江蘇 南京 210029)

堰流流量系數是溢洪道及水閘等泄水建筑物泄流能力計算中的關鍵參數，當前國內外學者在堰流流量系數的計算方面已有大量研究：毛昶熙[1]從水力學基本原理研究計算公式的合理性，并以模型試驗資料驗證，給出了堰閘淹沒泄流的流量系數表達式和大孔徑隧洞泄洪流量的計算公式；張紹芳[2]在系統地研究低堰溢流的水力特性的基礎上，給出通用于不同堰型和堰高、水頭范圍的溢流能力的計算方法；林孟程[3]通過對寬淺式溢洪道低堰體型研究，得出寬淺式溢洪道低堰流量系數隨堰頂水頭及定型水頭的變化規律；Issam A.Al-Khatib等[4]通過實驗室水槽模型試驗并利用多元回歸模型對數據擬合得到矩形復合寬頂堰流量系數及流速系數計算公式；Mohamad Reza Madadi等[5]通過實驗室水槽模型試驗研究了梯形寬頂堰迎水面坡度對流量系數的影響，并通過曲線擬合得到流量系數與迎水面角度的函數關系；Nourani Bahram等[6]應用數值模擬的方法分別引入2種智能模型計算寬頂堰流量系數，并對2種模型參數有效性及計算結果進行了評估和對比；馬欣等[7]通過水工模型試驗研究單宮V型迷宮堰不同布置方案的過流能力，并對試驗研究成果進行數學回歸擬合分析，得到可直接用于工程設計的V型迷宮堰過流能力計算公式。

水庫設計中，溢洪道控制段控制著水庫的水位和下泄流量，是溢洪道的咽喉[8]，其常用堰型有寬頂堰、實用堰，其中寬頂堰相對實用堰流量系數較小，但其結構簡單，施工方便，地基應力分布比較均勻，整體穩定性較好，因此在泄流量不大的中小型水庫中得到了較廣泛應用。

寬頂堰流量系數計算在溢洪道寬頂堰泄流能力計算中起著至關重要的作用，工程設計中主要采用現行水利行業規范[9](以下簡稱“SL規范”)中流量系數表、電力行業規范[10](以下簡稱“DL規范”)或水力計算手冊[11](以下簡稱“手冊”)中的經驗公式進行計算。SL規范中的流量系數采用與相對上游堰高P1/H及底坎形狀有關的二維表格，考慮因素比較全面，但要計算泄流能力的水位-泄流量曲線時，需要進行P1/H與r/H或cotθ(Δx/Δy)2個參數的二維線性內插，計算較為繁瑣；DL規范及手冊中流量系數是與相對上游堰高P1/H單變量有關的函數，計算時可編輯公式快速計算，運用方便，但是由于考慮因素單一，會導致計算精度較低或應用范圍較窄。

齊清蘭等[12]根據SL規范中流量系數表數據應用最小二乘回歸分析法擬合了有坎寬頂堰流量系數的經驗公式，計算精度高于DL規范公式，但是由于其擬合的流量系數公式是不同r/H或cotθ(Δx/Δy)值下的單變量P1/H公式，進行水位-泄流量曲線計算時參數r/H是跟水頭H有關的變量，仍需進行一次r/H線性內插，計算不夠方便；單長河等[13]采用二元非線性回歸分析法對多個數學模型進行分析，結合實測資料得到了無坎寬頂堰流量系數的經驗公式，克服了查表法多次內插帶來的不便，但是其擬合的經驗公式是以翼墻型式及寬度的收縮程度為自變量的表達式，與常用的規范及手冊上的自變量差別較大，使用仍不夠方便。為方便SL規范流量系數表格使用，本文將利用SL規范中數據采用二元非線性擬合的方法對數據進行擬合得到底坎為圓角的寬頂堰流量系數公式m=f(r/H，P1/H)，將其與電力規范公式比較，并對兩者計算誤差進行分析討論。

1 流量系數計算公式擬合

1.1 擬合原理

有理函數屬于簡單函數，它雖比多項式復雜，但用其近似表示函數時，卻比多項式靈活，更反映函數的一些特性[14]。因此本次二元非線性擬合將采用二元有理函數作為擬合函數。二元有理擬合就是尋求二元有理函數：

(1)

使之滿足下列插值條件：

r(xi,yj)=fij,(i=0,1,2,……m,j=0,1,2,……n)

(2)

式中P(x,y)、Q(x,y)——二元多項式；fij——樣本數據在(xi,yj)點的值。

吳曉韻[15]在逼近二元表格函數時，選用了二元有理函數，通過使性能指標J0(a)=極小來求解各項待定系數ai。本文根據吳曉韻[15]的思路選用式(3)對數據進行擬合，函數表達式為：

(3)

式中a1，a2，……，a9——待求系數。

令x=r/H，y=P1/H，則式(3)可表示為：

(4)

1.2 基礎數據

本研究所用樣本數據為SL規范中表A.2.3-1、A.2.3-2數據，由于底坎為直角或斜面時cotθ=0的情況與底坎為圓角時r/H=0為同一種情況，因此本次將底坎為直角或斜面時cotθ=0條件下的m值表數據與底坎為圓角時的表格數據結合作為本研究的樣本數據，見表1。

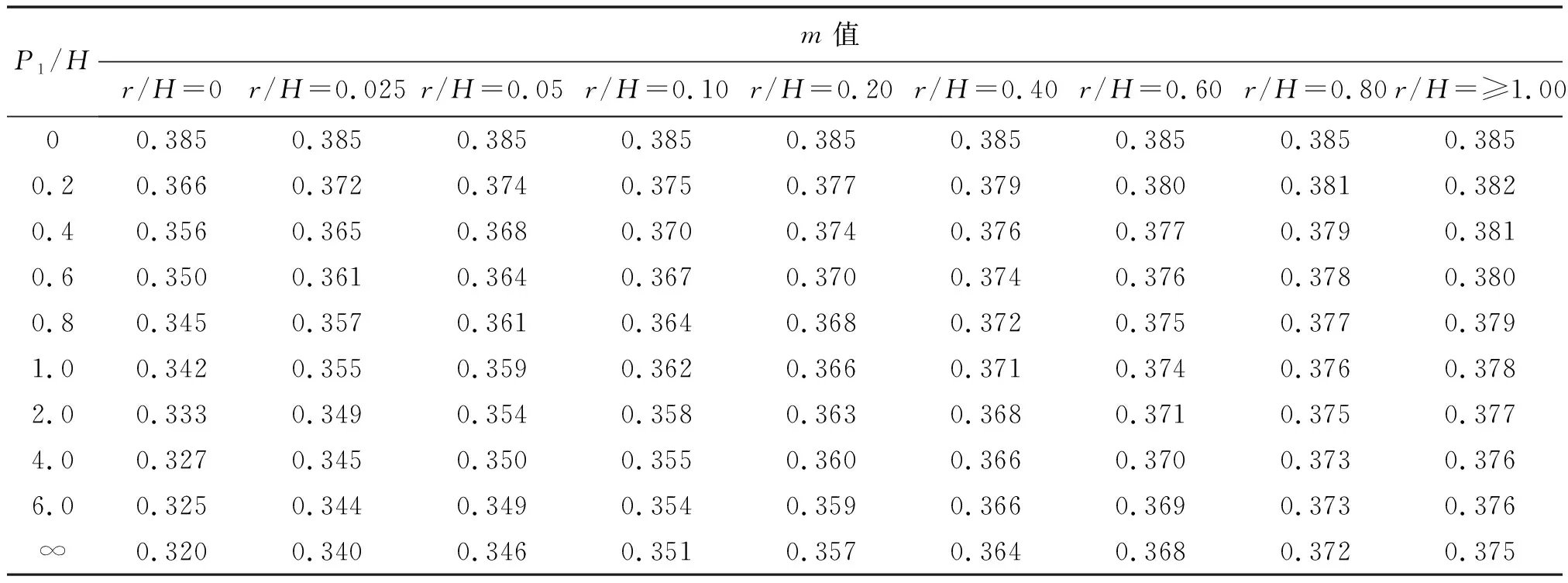
表1 底坎為帶圓角的寬頂堰流量系數m值

1.3 擬合結果

因基礎數據在P1/H∈(6，+∞)區間無明確數據，故本文進行擬合時僅采用P1/H∈[0，6.0]對應樣本數據。經擬合，求解出式(4)中各待定參數值及其相關性見表2，擬合函數曲面圖見圖1。

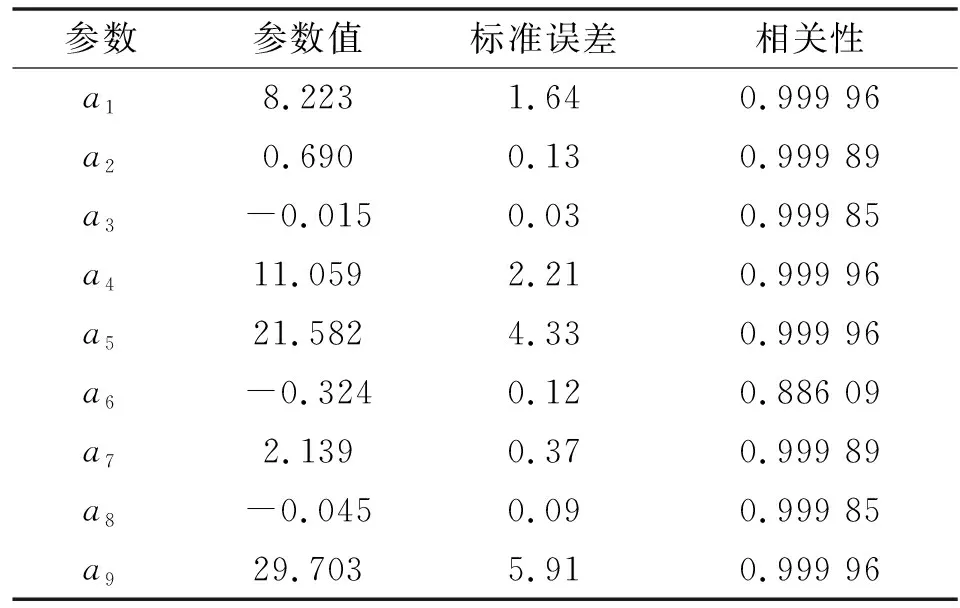
表2 函數待定參數值、標準誤差及相關性

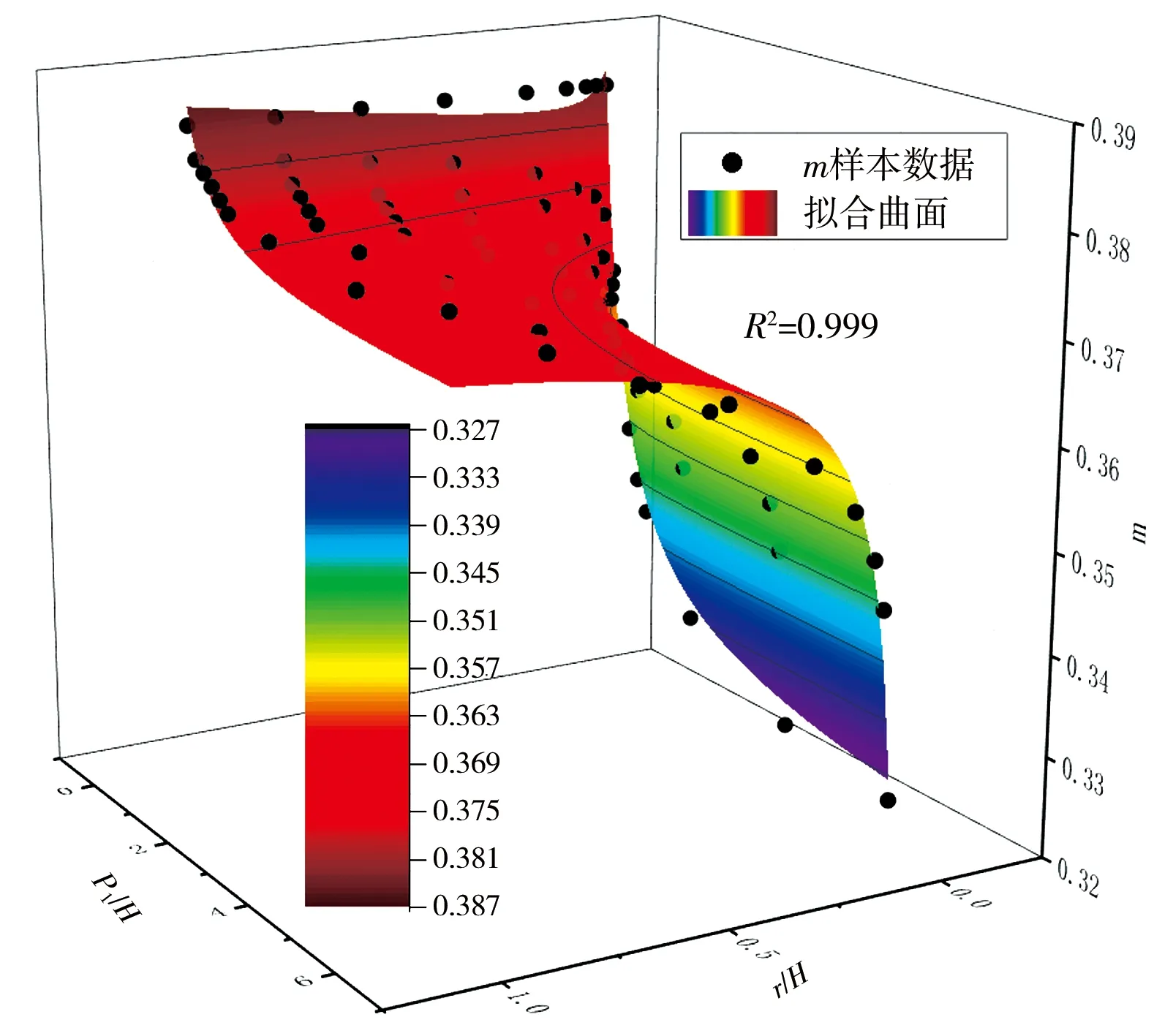
圖1 擬合函數曲面圖

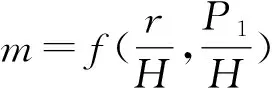
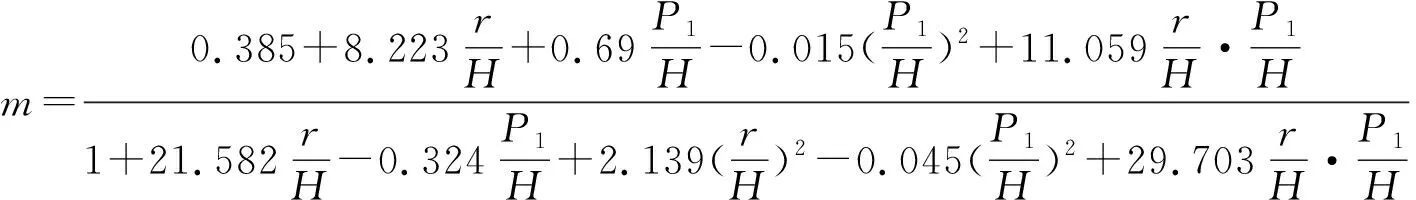
(5)

式中m——寬頂堰流量系數；H——堰頂水頭，m；P1——寬頂堰坎高，m；r——坎頂圓角半徑，m。各參數見圖2。

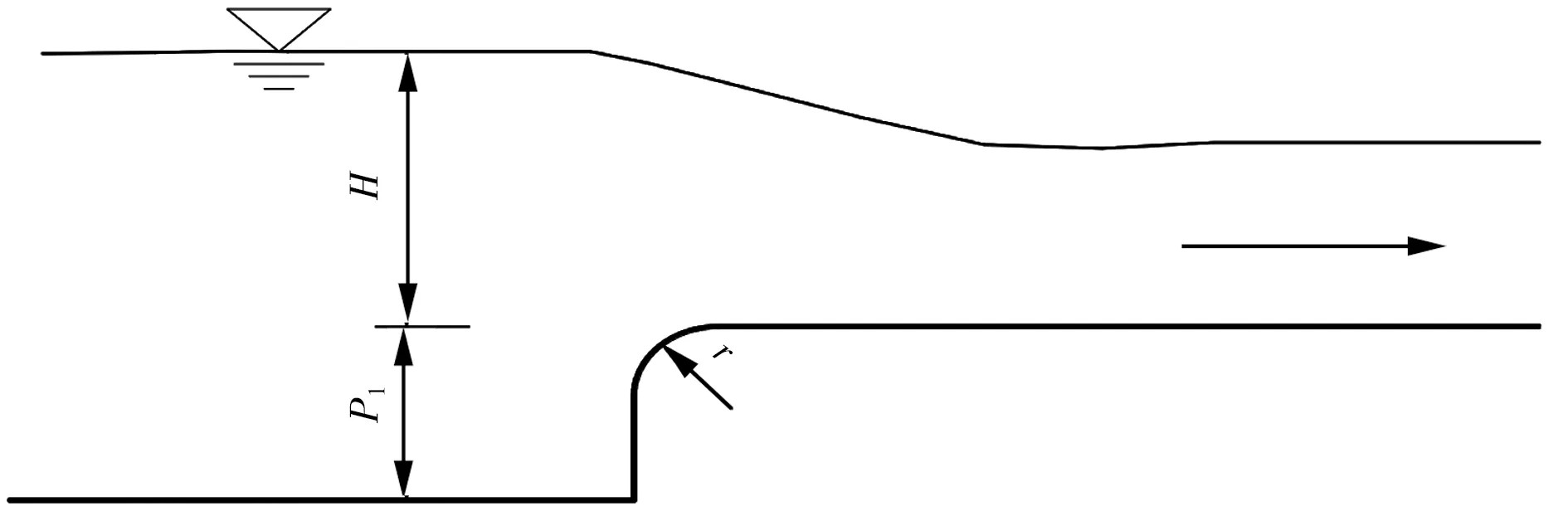
圖2 寬頂堰示意

2 公式比較與誤差分析

2.1 公式驗證比較

將SL規范表A.2.3-1、A.2.3-2數據及其線性插值結果作為標準值，分別用本次擬合公式及DL規范計算公式計算結果與標準值進行對比。DL規范寬頂堰流量系數m計算公式見式(6)、(7)。式中各參數同式(5)。

進口底坎為方角時：

(6)

進口底坎為圓角時：

(7)

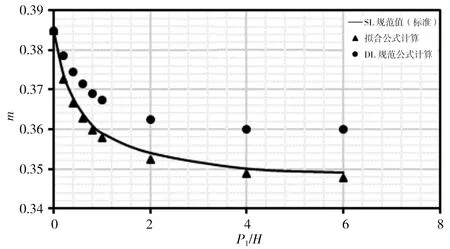
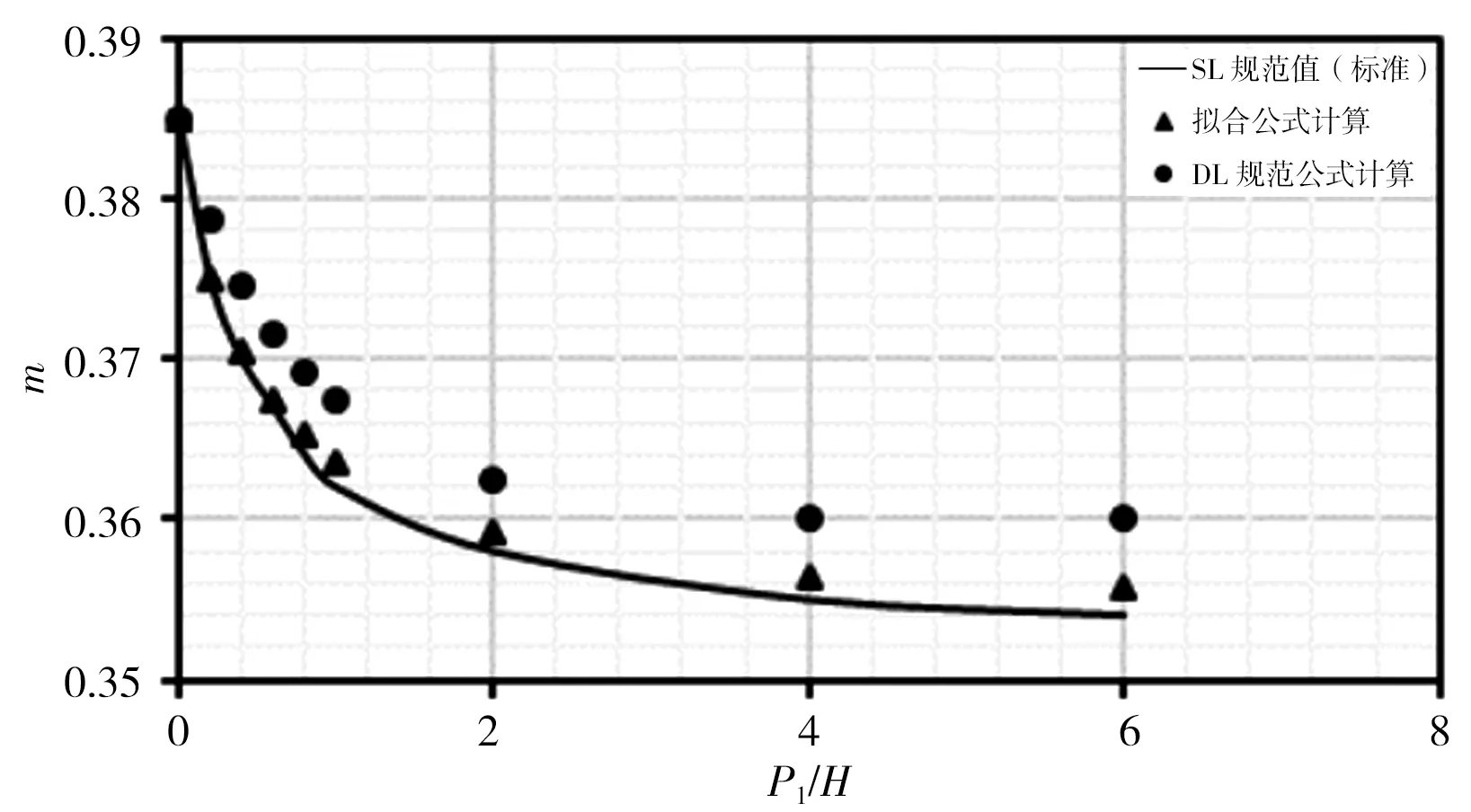
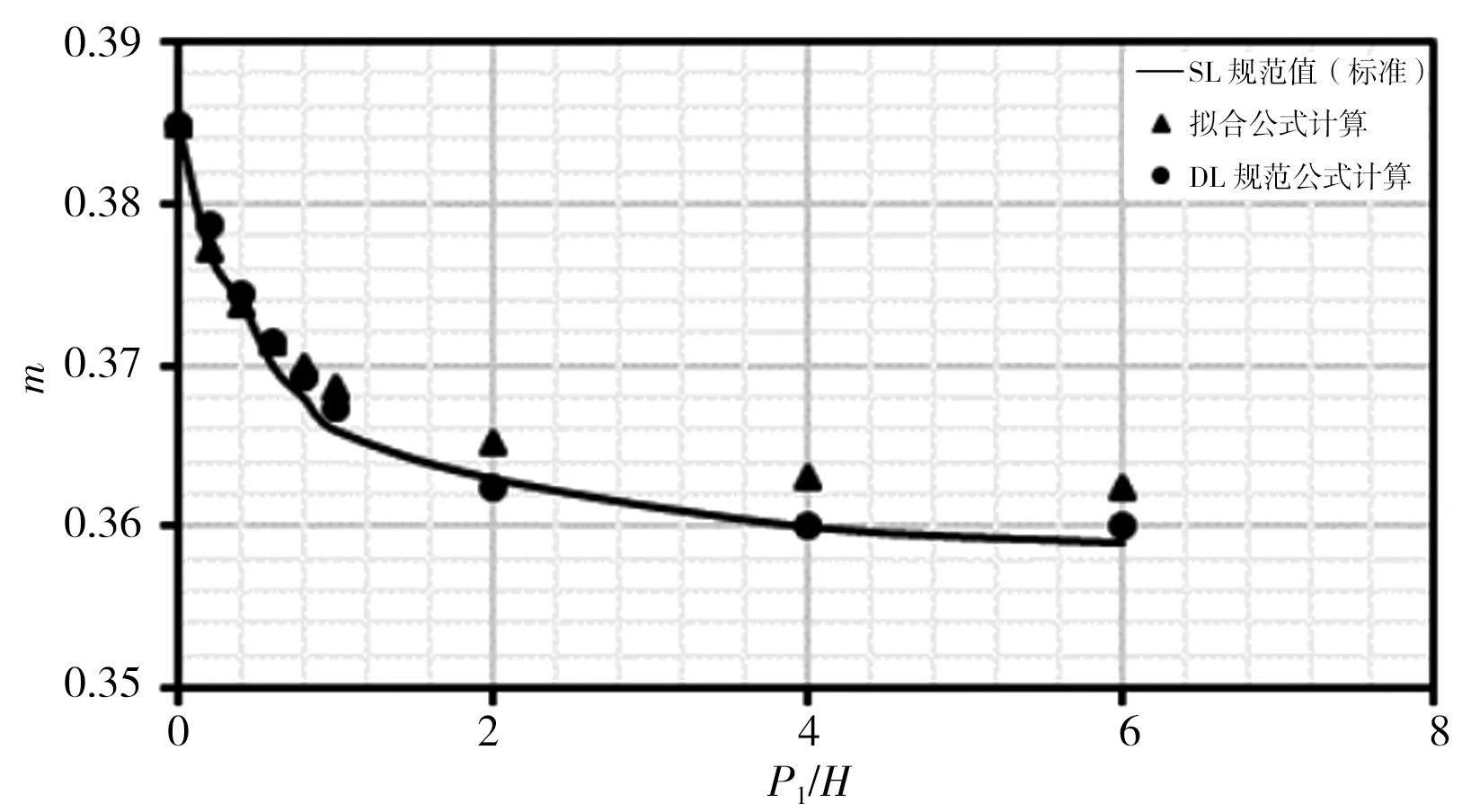
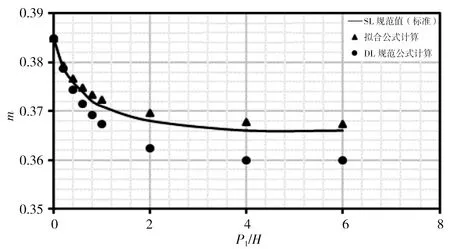
本次分別對各公式在r/H=0、r/H=0.025、r/H=0.05、r/H=0.10、r/H=0.20、r/H=0.40、r/H=0.60、r/H=0.80時，對應P1/H=0～6時計算結果進行比較，計算結果見圖3。由圖3計算結果可看出：①擬合式(5)計算出的流量系數m在r/H各取值下與SL規范表格標準值趨勢相同，且計算點與標準曲線基本重合；②DL規范式(6)和(7)計算流量系數m在r/H<0.20時，均位于標準值曲線之上，此時DL規范公式計算結果偏大，隨著r/H增大，計算點與標準曲線差距逐漸減小；③r/H=0.20時計算m值與標準曲線基本重合且優于式(5)計算結果；④r/H>0.20時，計算流量系數m均位于標準值曲線之下，此時DL規范公式計算結果偏小，隨著r/H增大，計算點與標準曲線差距逐漸增大。

綜上分析，總體而言擬合式(5)計算結果優于DL規范式(6)和(7)計算結果。

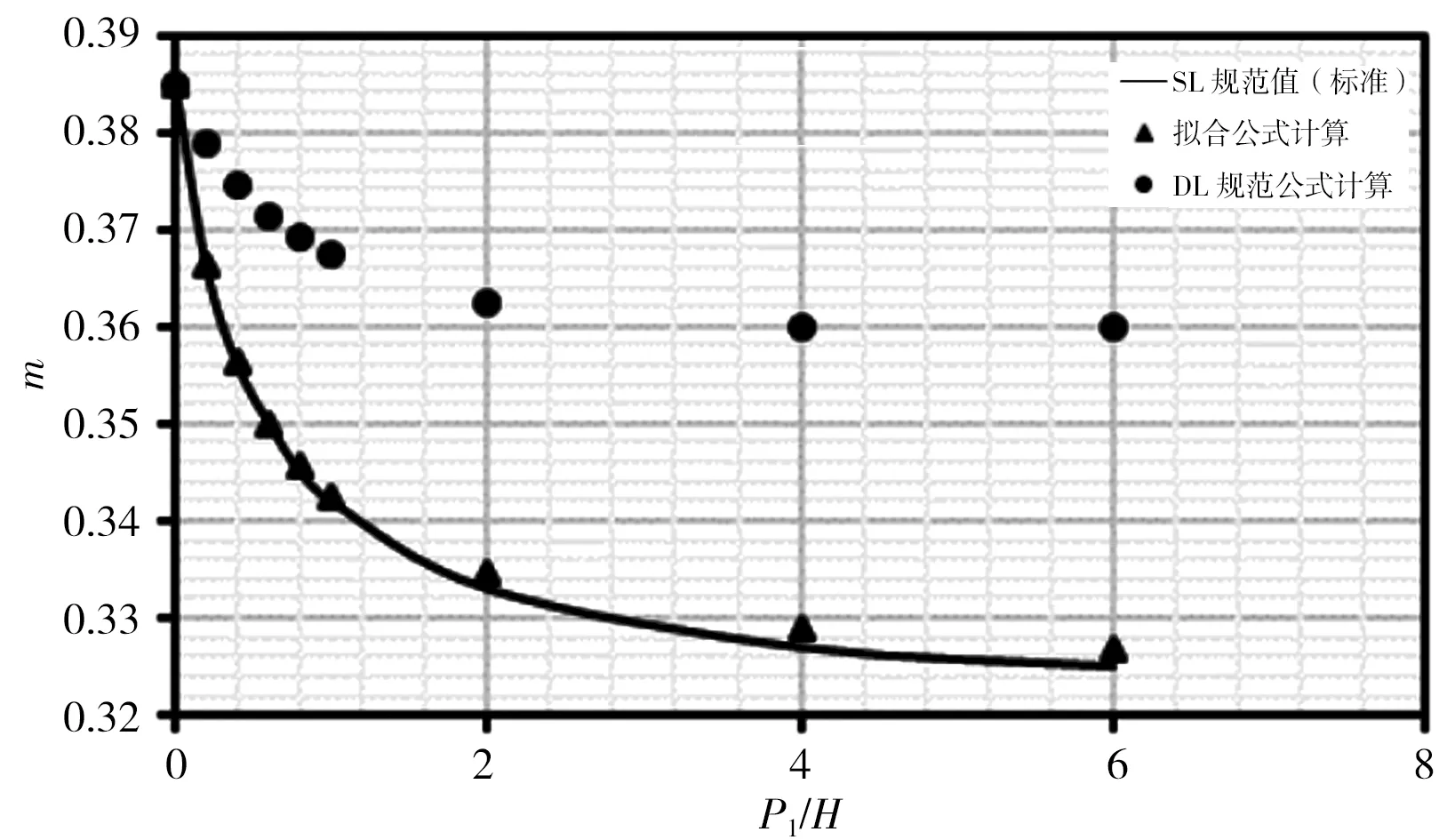
a)r/H=0

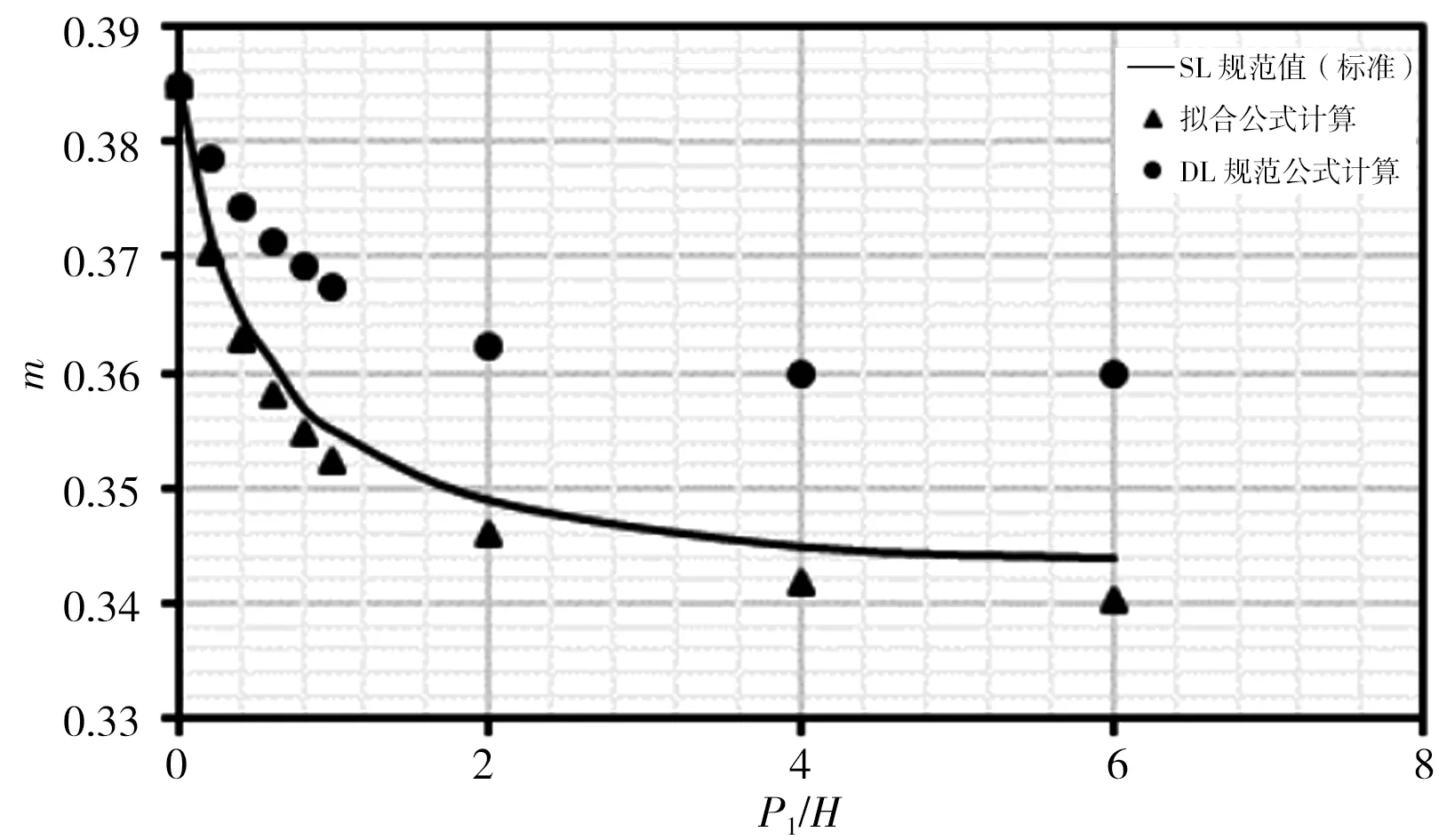
b)r/H=0.025

c)r/H=0.05

d)r/H=0.1

e)r/H=0.2

f)r/H=0.4

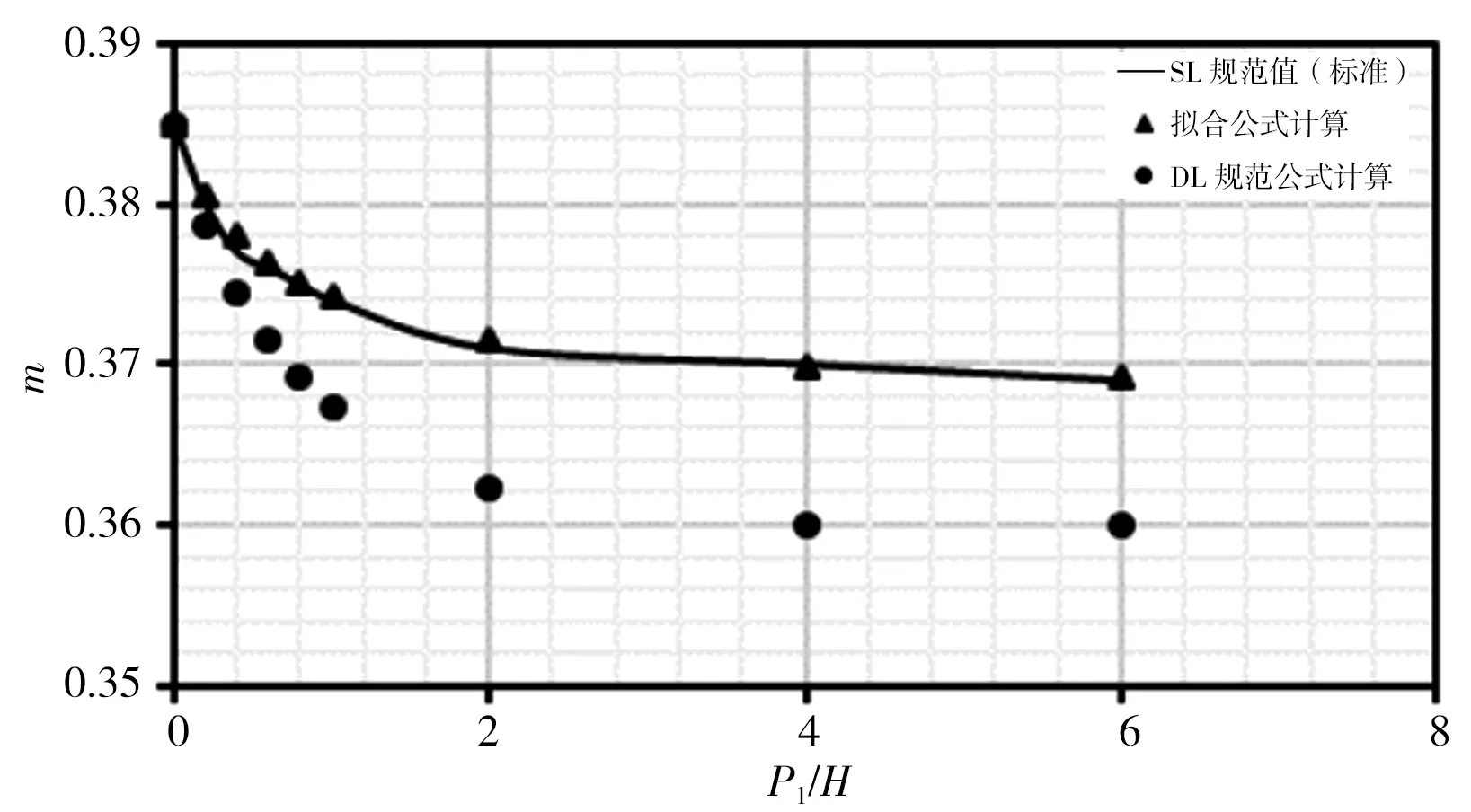
g)r/H=0.6

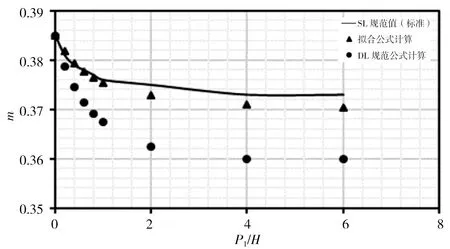
h)r/H=0.8

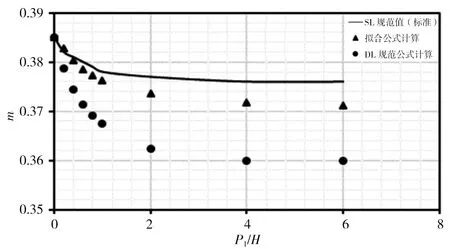
i)r/H≥1.0

2.2 計算誤差分析

為定量比較擬合式(5)與DL規范公式的計算精度，需對兩公式計算結果進行誤差比較。戴文鴻等[16]在比較穩定河道計算方法時采用了差異比(DR)、相對誤差(RE)、幾何平均偏差(GAD)3個指標，本文將采用這3項指標來分析比較計算值與標準值之間的誤差。指標計算式如下：

(11)

(12)

(13)

式中Cc——計算值；Cm——標準值；N——數據組數。

DR越接近1表示計算值與標準值越接近；RE越接近0表示計算值與標準值越接近；GAD越接近1表示計算值與標準值越接近。

經計算，不同r/H值下擬合式(5)與DL規范公式計算結果的平均相對誤差、平均差異比及平均幾何平均偏差對比見圖4。從圖中可看出如下結果。

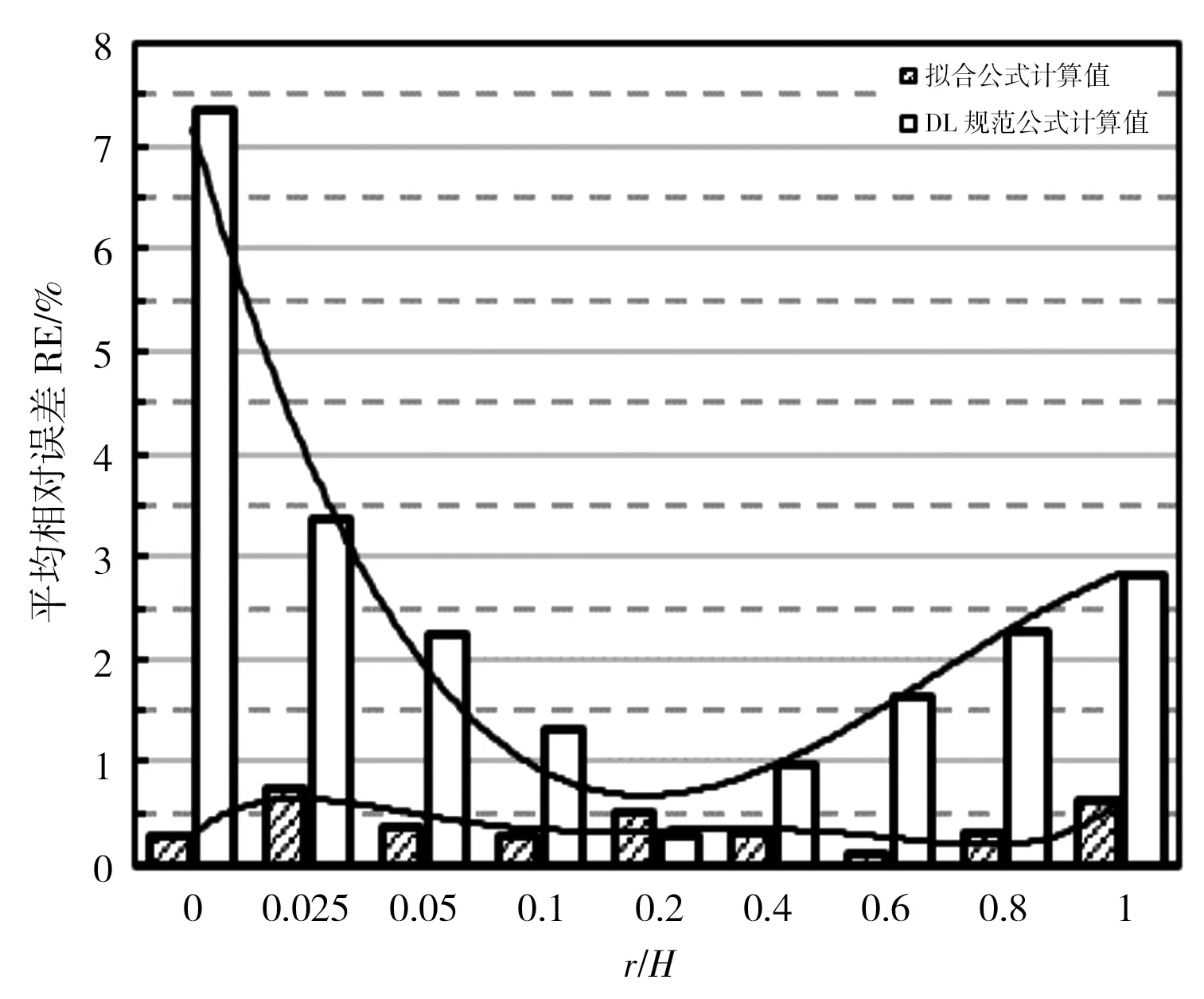
a)平均相對誤差

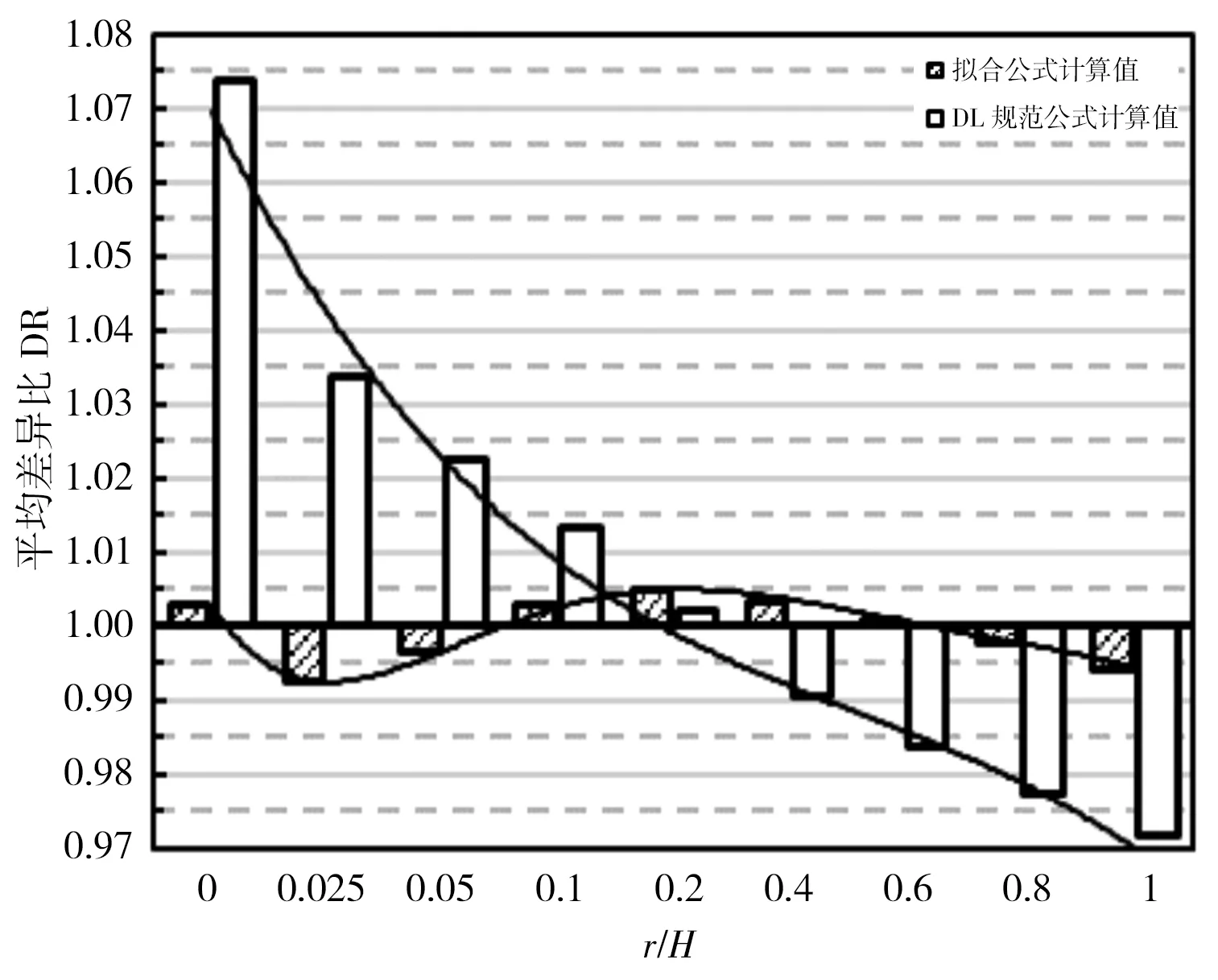
b)平均差異比

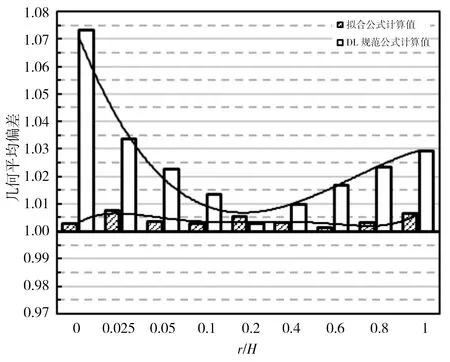
c)平均幾何平均偏差

a)平均相對誤差：擬合式(5)平均相對誤差在r/H各取值下均在1%以下，且在0.5%上下變化。DL規范公式平均相對誤差在r/H<0.20時從7.36%逐漸減小到1.33%，該范圍內平均相對誤差在1%以上；r/H=0.20時平均相對誤差達到最小值0.26%；r/H>0.20時平均相對誤差從0.97%逐漸增大到2.83%，該范圍內平均相對誤差在3%以內。

b)平均差異比：擬合式(5)平均差異比在r/H各取值下均在1±0.01以內。DL規范公式平均差異比在r/H<0.20時從1.07逐漸減小到1.01，最大變幅+0.07；r/H=0.20時平均差異比達到最小值1.002；r/H>0.20時平均差異比從0.99逐漸減小到0.97，最大變幅-0.03。

c)平均幾何平均偏差：擬合式(5)平均幾何平均偏差在r/H各取值下均在1～1.01以內，最大變幅+0.01。DL規范公式平均差異比在r/H<0.20時從1.07到1.01逐漸減小靠近1.00，最大變幅+0.07；r/H=0.20時平均差異比達到最小值1.003；r/H>0.20時平均差異比從1.01到1.03逐漸增大偏離1.00，最大變幅+0.03。

綜上分析：從整體水平上擬合式(5)各誤差指標變化范圍較小，且均在較優的范圍內；DL規范公式各誤差指標變化范圍較大，在r/H<0.20時偏離最優值較大，在r/H=0.20時最接近最優值，在r/H>0.20偏離最優值相對較小。因此擬合式(5)在r/H各取值下均適用，DL規范公式僅在r/H≥0.20時較適用。

3 擬合公式應用實例

選取貴州省某水庫溢洪道設計作為實例，采用擬合式(5)進行計算，并與查SL規范表格計算值進行對比。貴州某水庫溢洪道由引渠段、交通橋段、控制段、泄槽段、消力池段和海漫段等部分組成，溢洪道全長226.83 m，其中引渠段長47.41 m，交通橋段長10 m，控制段長15 m，泄槽段長92.05 m，消力池段長28 m，海漫段長34.37 m。溢洪道控制段堰型為有坎寬頂堰，坎高P1=1.50 m，堰頂高程為892.00 m，與正常蓄水位平齊。泄槽段坡比1.0∶2.3，全段無變坡，寬度由17.50 m收縮為12 m。消力池型式為底流消能，底板高程851.50 m，池深3.50 m，池長28.00 m。

設計計算分別選取坎頂圓弧半徑r=0、r=0.5P1=0.75 m、r=P1=1.5 m 3種型式，每種型式計算堰頂水頭范圍為0.2～15 m系列計算各流量系數。計算結果見表3。

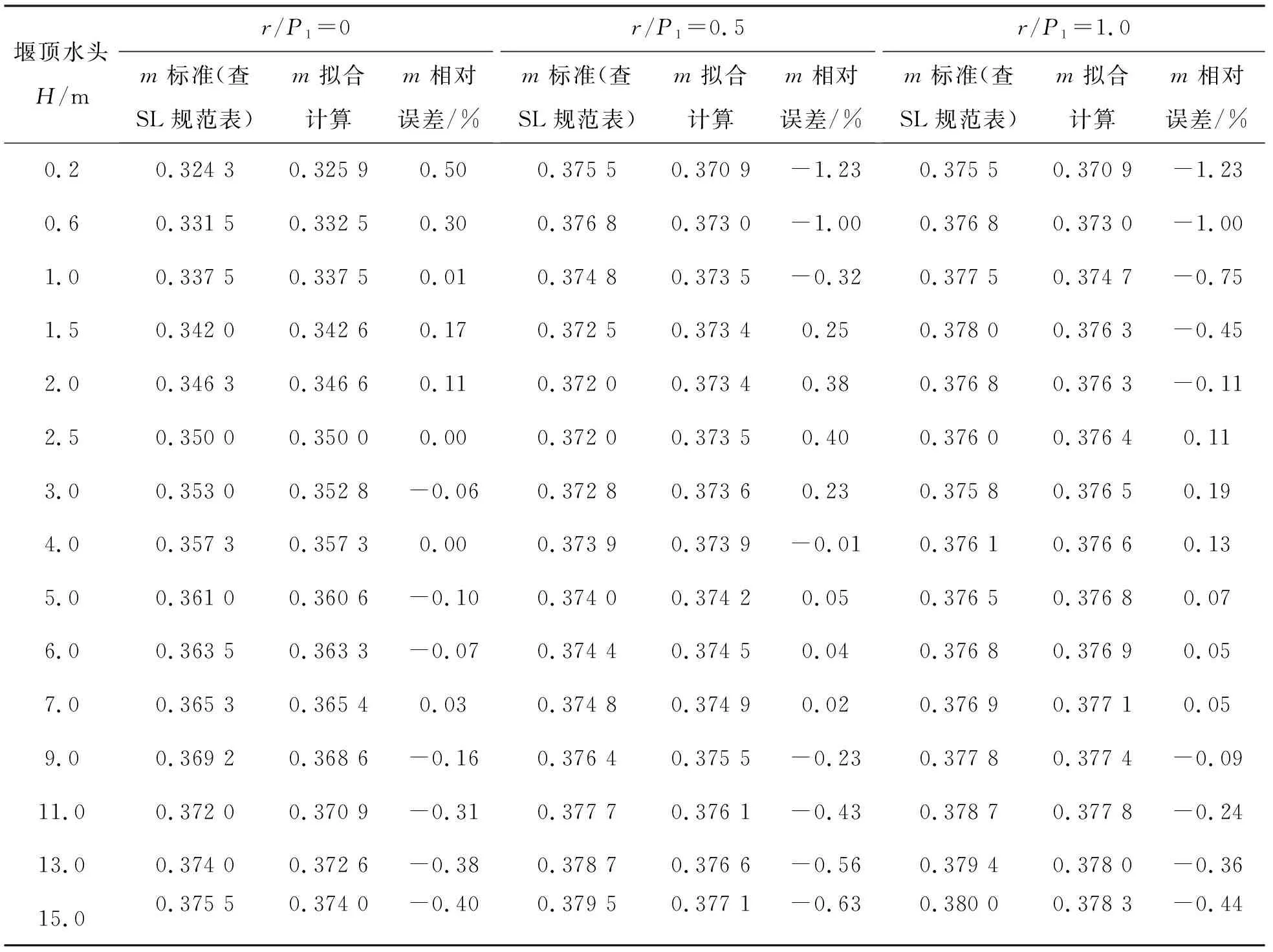
表3 不同圓角半徑各堰頂水頭下流量系數計算結果

將上表m標準值作為x坐標，對應m擬合計算值作為y坐標繪制于直角坐標系，見圖5。從圖中看出，r/P1=0時各點基本與“計算=標準”線重合；r/P1=0.5及r/P1=1.0時各散點均勻分布于“計算=標準”線附近，且大部分位于±1%誤差線之間，僅有個別點在-1%誤差線外，但較接近-1%誤差線。分析其原因，位于-1%誤差線以外的點為堰頂水頭H較小時的計算結果，當H較小且P1/H>6時將超出擬合式(5)的樣本范圍，在樣本數據范圍外式(5)計算精度難以保證。

因此，在工程設計中當P1/H≤6時可應用式(5)替代查SL規范表A.2.3-2計算寬頂堰流量系數；在P1/H>6時須對計算的結果進行分析，若坎高P1不大，P1/H>6時堰頂水頭H亦較小，此時式(5)計算結果偏小，在工程上偏安全，亦可用式(5)計算結果近似替代查SL規范表的值。

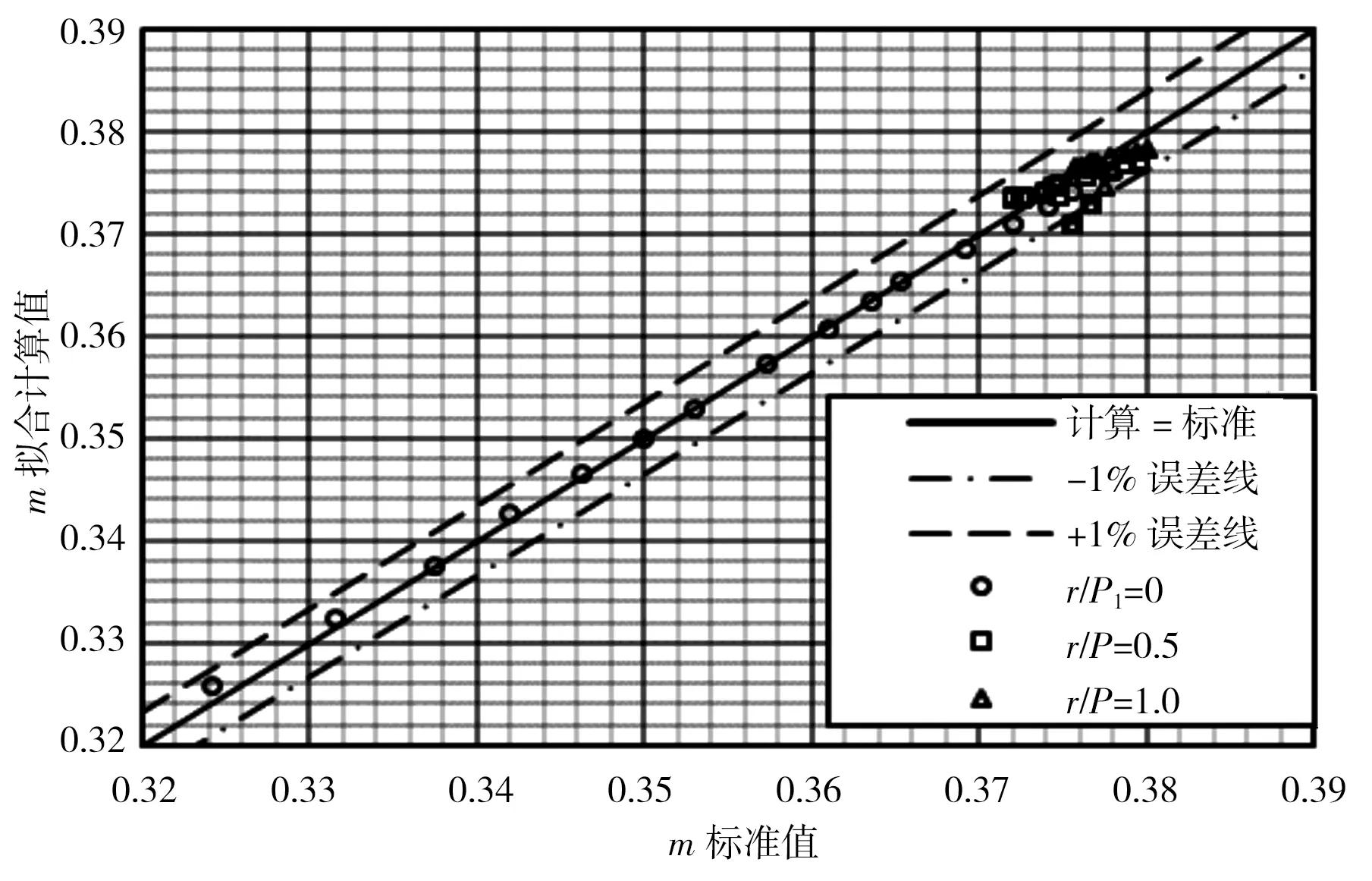
圖5 實例驗證

4 結論

a)選取SL規范表A.2.3-1、A.2.3-2數據作為樣本數據，應用二元有理插值函對數據進行擬合得到溢洪道寬頂堰流量系數的二元函數表達式m=f(r/H，P1/H)，該公式可避免查表多次內插的繁瑣工作。

b)經對擬合公式及DL規范公式進行驗證比較，擬合公式計算結果優于DL規范公式計算結果。

c)經對擬合公式及DL規范公式計算結果的平均相對誤差、平均差異比及平均幾何平均偏差三誤差指標比較，擬合公式在r/H各取值下均適用，DL規范公式僅在r/H≥0.20時較適用。

d)選取某水庫溢洪道設計作為實例，經過對計算結果分析，在工程設計中可應用擬合公式替代查SL規范表計算寬頂堰流量系數。