高超聲速4∶1橢圓錐橫流不穩定性實驗研究*

鄭文鵬 易仕和 牛海波 霍俊杰

(國防科技大學空天科學學院，長沙 410073)

在馬赫6 高超聲速靜風洞中針對長短軸比為4∶1 的鈍頭橢圓錐表面橫流不穩定性進行了實驗研究.綜合利用溫敏漆技術、基于納米粒子的平面激光散射技術和Kulite 傳感器壓力測試對模型表面橫流區域內的溫度分布、邊界層流動結構以及模型表面壓力進行了測試.研究了橢圓錐表面橫流控制區域邊界層轉捩機理，來流單位雷諾數和攻角對邊界層轉捩的影響規律，得到以下結論:在風洞噪聲模式下，長短軸比為4∶1 的橢圓錐模型表面中心線與前緣線之間橫流區域的邊界層轉捩是由橫流的行進波控制的，未發現橫流定常渦的足跡，行進波的特征頻率在20 kHz 左右;來流單位雷諾數增大時轉捩位置會提前，行進波的頻率和幅值均增大;在一定攻角范圍內，隨攻角增大迎風面邊界層轉捩位置推遲，行進波特征頻率變化不大但能量減弱，攻角繼續增大時轉捩現象消失.

1 引言

高超聲速流動中，當邊界層處于不同流動狀態時熱流、摩阻等參數會存在巨大差異，研究由層流到湍流的轉捩機理以及合理預測邊界層轉捩位置對高超聲速飛行器熱防護設計、飛行器表面流動控制等具有重要的參考意義.而在真實飛行條件下，飛行器表面邊界層往往表現出強烈的三維性，此時橫流不穩定模態在邊界層轉捩中可能會占主導地位.

橫流是指壁面邊界層內部在壓力梯度作用下產生的垂直于無黏流方向的速度分量，由于壁面處和邊界層外緣橫流速度分量均為0，故邊界層內速度剖面存在拐點，這是橫流不穩定性的來源.為研究橫流不穩定性主導的三維邊界層轉捩問題，早在20 世紀90 年代Kimmel 等[1]便通過計算驗證了橢圓錐幾何構型提供了橫流產生所必需的壓力梯度，且能放大橫流不穩定性效應，可作為理想的實驗模型.美國和澳洲共同開展的HIFiRE-5 項目采用的也是長短軸比為2∶1 的橢圓錐模型[2-4].

Choudhari 等[5]以及Paredes 和Theofilis[6]的研究結果表明，橢圓錐表面的流動可分為3 個區域:短軸附近中心線區域、中心線與前緣線之間的區域以及前緣線附近區域.其中，短軸附近中心線與前緣線之間是可能由橫流不穩定性主導控制轉捩的區域，存在橫流定常渦和橫流行進波兩種橫流的不穩定模態以及橫流定常渦的二次失穩[7，8];短軸附近中心線區域由于橫流效應下流動會從兩側附著線向此處匯聚[6，9]，邊界層厚度會變厚，并可能產生不穩定的流向渦結構;前緣附著線附近則主要由第二模態控制[10].

目前關于橫流不穩定性已經有了大量的數值模擬和風洞實驗結果，取得了一系列的研究成果.對于不可壓縮流動[11-14]，在低噪聲的飛行環境中或靜風洞中，橫流定常渦占主導地位，而在噪聲環境和傳統的風洞中，則是趨向于橫流行進波占主導地位;橫流定常渦通常出現在模型存在定常擾動的條件下，例如表面的粗糙度等其他穩定的擾動條件，而橫流行進波則是由于自由來流中的噪聲和/或擾動而產生的漩渦擾動，被裹挾在邊界層中不斷發展而產生的;橫流定常渦的二次失穩是定常橫流渦經過線性增長、非線性飽和階段后發生的，可以快速演變為湍流結構.對于可壓縮流動，即流動為超聲速或高超聲速時，關于橫流不穩定性規律也有比較深入的研究.數值計算方面，Saric 和Reed[8，15]指出可壓縮流動中橫流不穩定性規律與不可壓縮流動中是相似的.Kimmel 等[16]在馬赫8 條件下對長短軸比為2∶1 的橢圓錐模型橫流不穩定性規律進行了數值研究，發現在橢錐兩側“肩部”附近橫流行進波占主導地位，且當人工引入表面粗糙度時出現了橫流定常渦;Dinzl 和Candler[17]利用DNS 方法分析了在馬赫6 條件下，不同來流單位雷諾數和模型表面粗糙度時橫流定常渦的變化規律，發現與表面粗糙度相比，擾動波波長對來流單位雷諾數的變化更敏感，說明自由來流中噪聲條件對橫流渦的影響更顯著;Moyers 等[18]通過耦合非線性拋物線穩定方程與空間雙葉方程，以橫流定常渦二次失穩中性點位置來預測轉捩位置.

實驗研究方面，Berridge 等[19]利用溫敏漆(temperature sensitive paint，TSP)技術在風洞的靜音模式和傳統噪聲模式下觀察到了橫流定常渦的足跡.普度大學團隊在BM6QT 馬赫6 靜風洞[20-27]中對長短軸比為2∶1 的橢圓錐模型進行了針對性的風洞實驗，在靜音模式下，利用油流實驗、TSP 實驗和紅外成像技術均測得了橫流定常渦的蹤跡，同時在該模式下利用Kulite 傳感器測得了橫流行進波的特征信號，特征頻率大約為45 kHz且隨單位雷諾數的升高而增大，證明了在靜音模式下橫流定常渦和行進波會同時存在;在傳統噪聲模式下，只在油流實驗中觀測到了定常渦的蹤跡，在TSP 實驗和紅外像中沒有出現，而且此模式下也沒有捕獲到橫流行進波信號;之后Juliano 等[28]在波音公司/美國空軍科學研究室的馬赫6 風洞中利用紅外成像技術驗證了之前TSP 結果與紅外熱成像結果的可靠性.Borg 等[29]還同時在傳統TAMU ACE 高超聲速風洞中進行了同樣的實驗，通過與靜風洞數據對比研究來流噪聲對流場特征的影響規律，實驗表明傳統風洞與靜風洞噪聲模式下模型壁面的壓力測試結果是極其相近的，但是傳統風洞中測得的低頻特征信號并不能確定是否為橫流行進波，噪聲水平的影響規律也無法得到;Hembling等[30]在美國空軍學院馬赫6 風洞中做了類似的工作，他們利用紅外熱成像技術研究不同來流噪聲對橢圓錐橫流不穩定性的影響，未觀察到橫流渦足跡，但轉捩發生位置與在其他風洞中確定橫流渦主導轉捩時的結果符合，故推測其轉捩機理相同，且證明了來流噪聲會影響轉捩位置.Juliano 等[31，32]還通過熱電偶數據計算熱流并分析確定轉捩位置，得出橢圓錐橫流控制區域的轉捩對攻角和偏航角變化比較敏感.

目前，已有的關于橢圓錐模型邊界層轉捩問題的實驗研究成果主要集中在HiFIRE-5 項目中長短軸比為2∶1 的38.1%縮比橢圓錐模型[33，34]上，已經證明了橫流定常渦和橫流行進波的存在，并研究了來流噪聲水平、表面粗糙度等因素對橫流不穩定模態主導轉捩的影響，但仍然存在明顯的不足，比如不同來流條件下橫流不穩定模態控制轉捩的類型仍存在不確定性，研究橫流模態類型時采用的實驗技術單一導致結論的確定性有限，以及真實飛行條件下攻角和來流雷諾數等重要因素對橫流不穩定性控制轉捩的影響規律研究欠缺等.

本文實驗研究在更接近新型飛行器外形的4∶1 鈍頭橢圓錐上進行，采用了多種實驗方法從定性和定量方面對實驗工況下主導轉捩的橫流不穩定模態類型做了全面的論證，保證結論的可靠性，并系統研究了橢圓錐表面橫流不穩定性在不同攻角、來流單位雷諾數條件下的變化規律，可為后期數值模擬與實驗研究提供依據和參考.

2 實驗設備、模型與技術

2.1 風洞設備

本文中實驗是在國防科技大學自主研制的吹吸式高超聲速靜風洞(圖1)中進行的，風洞的運行馬赫數為6，噴管出口尺寸為φ300 mm.為降低風洞噪聲水平，風洞穩定段設置有多孔倒錐、阻尼網和消音夾層等整流裝置，位于噴管喉道上游附近的抽吸裝置可抽走喉道壁面附近的渦結構，使邊界層保持為層流狀態.抽吸裝置開啟時為靜音模式，關閉時為噪音模式，本文實驗是在噪聲模式下進行的.同時，風洞上游的氣流加熱和保溫裝置可以實現來流的總溫控制，最高可達600 K;通過調節總壓(最大總壓為3 MPa)可實現來流單位雷諾數的變化控制.目前在該風洞內已經進行了大量的關于邊界層轉捩問題的實驗研究[35-37].

圖1 高超聲速靜風洞照片Fig.1.Picture of hypersonic static wind tunnel.

2.2 實驗模型

本文采用的是長短軸比為4∶1 的橢圓錐電木材料模型，長軸為75 mm，短軸為18.75 mm，模型長度為400 mm，頭部為短半徑為4.5 mm 的半橢球形.圖2 為實驗模型的示意圖.

圖2 模型示意圖Fig.2.Model diagram.

2.3 實驗技術

本文綜合利用TSP 技術、實驗室自主開發的高時空分辨率的基于納米粒子的平面激光散射(nano-tracer-based planar laser scattering，NPLS)技術以及Kulite 壓力傳感器測量以實現對該實驗模型邊界層轉捩規律及機理的多方面數據支持和印證.

2.3.1 TSP 技術

TSP 技術是利用溫敏涂料的分子發光特性，標定并擬合分子發射光強與絕對溫度之間的函數關系，通過相機接收模型表面涂料發射的光強信息來得到模型表面溫度的非接觸測量手段.硬件設備包括TSP、光源、濾光片以及相機.本文選用的TSP在光源作用下，發射光波長主要分布在400—700 nm范圍內，模型表面底漆上均勻噴涂溫敏涂料，厚度為20 μm，標定溫度范圍為5—80 ℃ (278—353 K)，標定曲線[35]如圖3 所示，擬合程度較高.由擬合曲線得到標定方程:

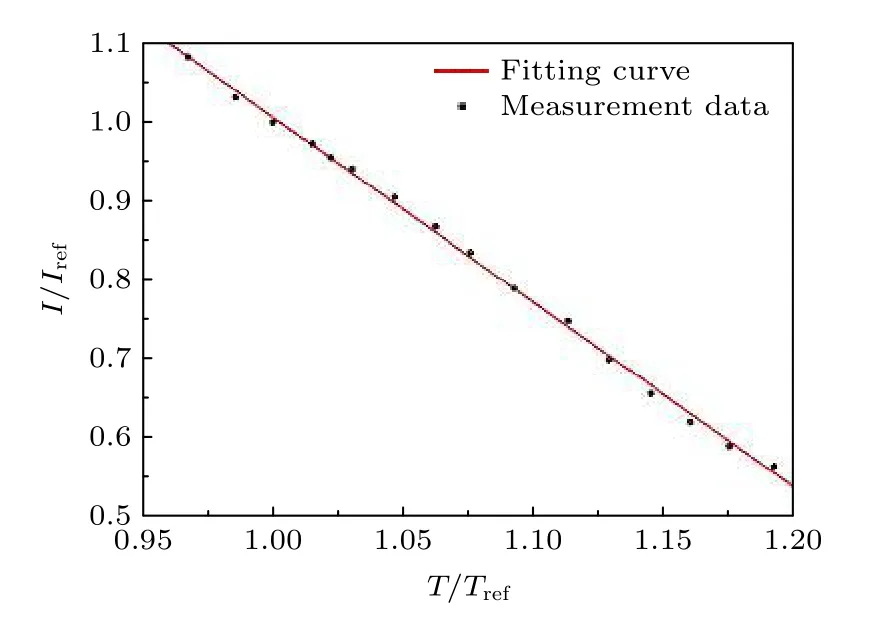
圖3 標定曲線Fig.3.Calibration curve.

其中I，T分別為模型表面的光強和溫度，Iref，Tref為參考光強和溫度.

實驗中采用的光源為中心波長為365 nm 的LED 光源;濾光片為濾光特性為460 nm 長波通的彩色濾光片，可濾掉波長小于460 nm 的光;相機采用CCD 相機，分辨率為2048 × 2456，分別采集光源開啟前Ilight-off、光源開啟后Ilight-on以及風洞運行時Iwind-on三組圖像，則可得光強比率的計算公式:

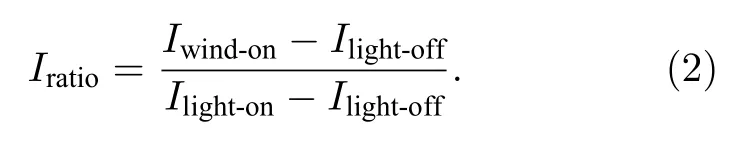
將(2)式代入方程(1)可算得模型表面的溫度分布.

2.3.2 NPLS 技術

NPLS 技術[36，37]是以傳統平面激光散射技術為基礎，創新采用納米級粒子作為示蹤物的高時空分辨率、高信噪比的流動顯示技術，可清楚反映邊界層的精細流動結構，且在時間相關前提下可以定量估算擾動波波長、頻率等信息.NPLS 測試系統(圖4)由ND-YAG 激光器、粒子發生器、CCD 相機以及同步控制器組成，工作原理為:離子發生器產生的納米粒子與來流在風洞上游均勻混合后經過噴管進入試驗段，在同步控制器作用下，CCD 相機與激光器按照既定時序協同工作，捕獲平面激光照亮的粒子形成高分辨率的流動顯示圖像，圖像記錄時間為6 ns，時間相關圖像的時間間隔由激光器發出的兩束光的時間間隔決定，本文中時間相關的兩幅圖像的時間間隔為5 μs.

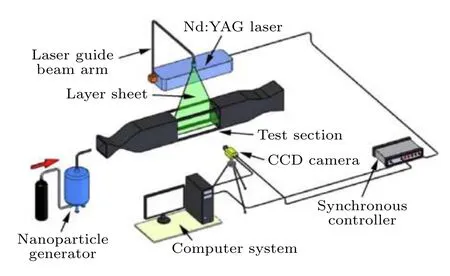
圖4 NPLS 技術原理圖Fig.4.Schematic diagram of NPLS technique.

2.3.3 Kulite 傳感器測試

壓力傳感器測量可以捕捉壁面壓力信號的主頻成分，以此確定模型邊界層內擾動波的特征頻率，這是判斷擾動波類型的關鍵信息.本文使用的是Kulite 壓力傳感器，傳感器的布置位置是在TSP圖像基礎上選擇關鍵流動區域而確定的，測點位置及測點分布見表1 和圖5.

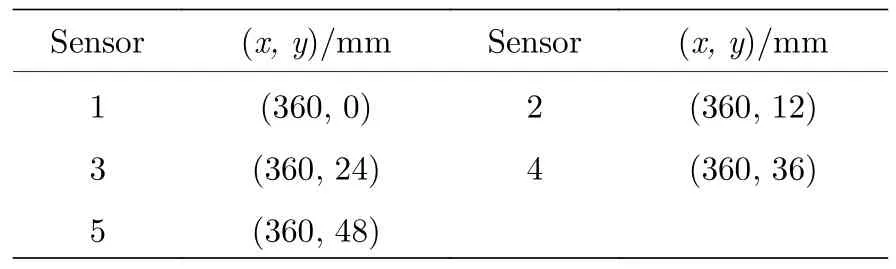
表1 傳感器測點位置Table 1. Sensor measuring point position.

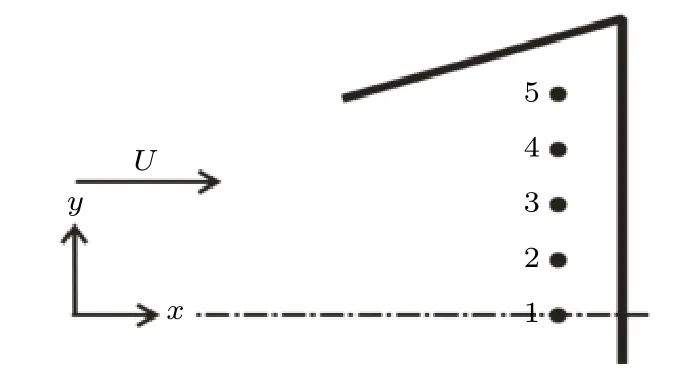
圖5 傳感器分布示意圖Fig.5.Distribution diagram of sensors.

3 結果與討論

3.1 典型工況下邊界層轉捩機理分析

圖6 顯示的是攻角為0°，來流單位雷諾數為1.3 × 107m—1時模型表面的溫升分布云圖.模型兩邊極高溫的區域為前緣線影響的區域，中心線的低溫區域為短軸附近中心線影響的區域，前緣線與中心線之間的區域為本文研究的重點區域，在此區域內發生的邊界層轉捩是由橫流不穩定性主導的.從圖6 的云圖可以看出:在流向210—320 mm 左右的范圍內，靠近前緣線附近為黃色的高溫區域，靠近中心線附近出現一片低溫區域，但比中心線的溫度要高，這是由于模型表面邊界層受到高超聲速氣流繞過鈍頭細長體模型時在模型表面形成的熵層的影響.在320—400 mm 左右的范圍內，溫度突然陡升，出現了沿中心線對稱分布的兩片類似三角形的高溫區域，該區域在模型尾部的展向寬度大約為30 mm，兩側溫度比類三角形高溫區域要低.與長短軸比為2∶1 的橢圓錐模型在噪聲條件下的實驗結果相似，長短軸比為4∶1 的光滑橢圓錐模型表面的高溫區域中未出現明顯的條帶狀結構，故推測模型表面不存在橫流定常渦.

為確定類三角形高溫區域的形成原因，利用NPLS 技術沿圖6 中虛線位置拍攝模型表面的邊界層流動狀態，得到了時間相關的兩幅邊界層精細流動結構的圖像(圖7)，圖像下方灰色楔形區域為模型壁面區域，白色亮線是由激光打到壁面處產生的散射光引起的，壁面上方灰度值最大的流動結構為邊界層，其余為主流區域;圖像分辨率為0.147 mm/pixels，兩幅圖片的時間間隔為5 μs.

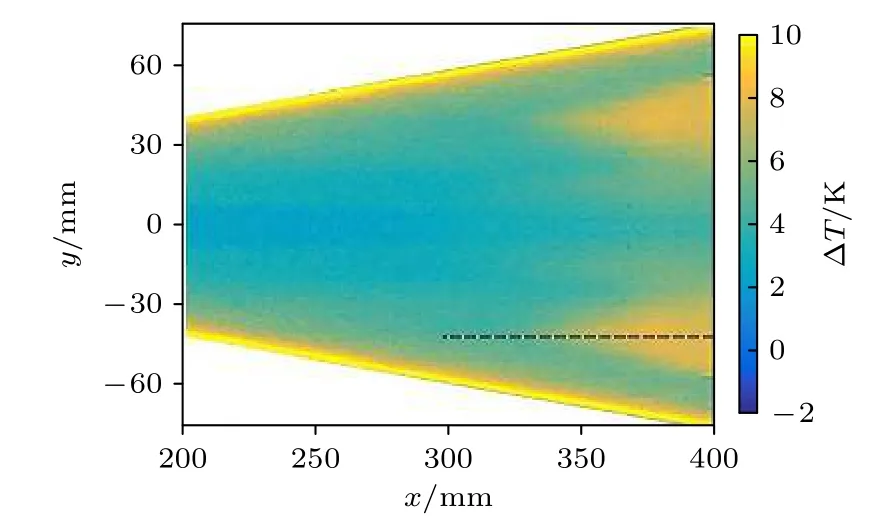
圖6 溫升分布云圖(0°，Re=1.3 × 107/m)Fig.6.Contour of temperature rise distribution (0°，Re=1.3 × 107/m).

圖7 時間相關的NPLS 圖像Fig.7.NPLS images with time correlation.

從圖7 可以看出:在220 mm 以前的范圍內，此時屬于前緣線區域的影響范疇，由于該范圍內邊界層厚度太小被壁面散射光遮住所以幾乎觀察不到邊界層;在220—320 mm 的范圍內，起初可以隱約看到層流邊界層，隨流向方向發展邊界層厚度逐漸變大，說明邊界層內部可能出現了擾動;在320 mm 左右處可以觀察到明顯的大尺度的擾動波結構，且靠近模型尾部的擾動波的幅值是最大的，但還沒有出現破碎結構，尚處于邊界層轉捩的早期階段.同樣地，沿圖6 中虛線位置提取TSP 圖像的溫升曲線(圖8)，根據溫升變化的趨勢可判斷，沿虛線位置上，模型表面的溫度是從x=325 mm左右的位置開始出現陡升，這與NPLS 圖像中擾動波結構出現的位置是符合的，可以說明類三角形高溫區域的出現是由邊界層轉捩引起的，但未完全轉捩，處于轉捩早期的過渡時期，轉捩陣面的形狀呈沿中心線對稱的兩個類似三角形形狀.由于中心線與前緣線之間的區域是由橫流不穩定性占主導，且從NPLS 圖像中可以看出擾動波是非定常結構，所以該區域內邊界層轉捩應該是由橫流的行進波控制的.

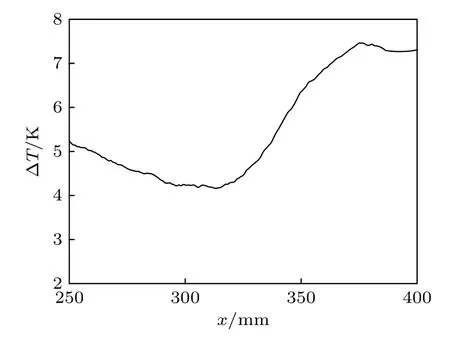
圖8 溫升曲線Fig.8.Temperature rise curve.

由于時間相關的兩幅圖像在微秒級的時間間隔內，邊界層流動結構發生的變化是極其微小的，甚至可以忽略，故可以用來估算擾動波結構的頻率信息.取圖7 兩幅圖像中標記的擾動波結構，通過圖像分辨率、像素信息與實際尺寸之間的對應關系，可以算得擾動波的波長λ ≈31.12mm，且在5 μs的時間間隔內擾動波行進的距離 Δx3.23 mm，利用平均速度代替瞬時速度可知擾動波行進速度的計算公式為cΔx/Δt，再由頻率的計算公式fc/λ，可推得該擾動波的頻率可以表示為fΔx/(Δt·λ)≈20.79kHz.

圖9 所示的是利用Welch 方法對攻角為0°、來流單位雷諾數為1.3 × 107m—1時Kulite 傳感器測得的風洞穩定運行時3 s 內的壓力數據進行計算得到的功率譜結果和傳感器底噪功率譜結果.由底噪結果可知，傳感器本身存在尖銳的電信號，與流動結構無關，功率譜曲線覆蓋全部的頻率無主頻信號，說明傳感器是正常工作的.根據圖9 結果可以看出:在57 和88 kHz 左右出現的尖銳的峰值信號為電信號，并非流動結構引起;位于中心線上的測點1 和位于轉捩陣面外緣到中心線范圍內的測點2 均存在4 kHz 左右的主頻信號;測點3—5 則屬于橫流控制區域類三角形轉捩陣面的范圍內，可以觀察到3 個測點處均出現了明顯的能量峰值，測點3 在17 kHz 左右，測點4 在21 kHz 左右，而測點5 出現在19 kHz 左右，根據傳感器的布置位置，測點5 的位置最接近于虛線位置，且特征信號的頻率與NPLS 圖像估算得來的擾動波的頻率基本符合，所以我們可以判斷，橫流控制區域內出現的類三角形的邊界層轉捩區域是由橫流的行進波占主導控制的，行進波的特征頻率大概在20 kHz 左右，且轉捩區域內還處于由層流到湍流的過渡階段，出現大尺度的擾動波結構，但未出現破碎結構以及湍流結構.

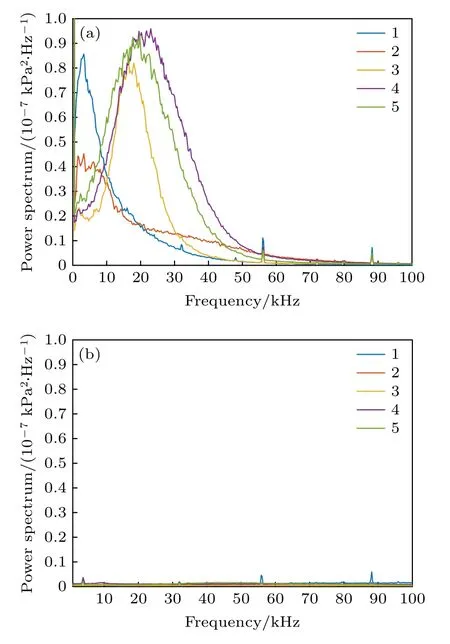
圖9 功率譜計算結果 (0°，Re=1.3 × 107/m) (a) 風洞運行時;(b) 底噪Fig.9.Power spectrum calculation results (0°，Re=1.3 ×107/m):(a) During wind tunnel operation;(b) noise of background.

3.2 來流雷諾數對轉捩的影響

單位雷諾數表征的是慣性力與黏性力的比值.在高超聲速條件下，來流單位雷諾數是影響壁面附近邊界層穩定性的重要因素之一.從一般意義上來講，在高雷諾數的條件下，慣性力遠遠大于黏性力，此時黏性力無法維持邊界層穩定的層流狀態，邊界層就會發生轉捩現象.為研究來流單位雷諾數對橢圓錐邊界層轉捩的影響規律，圖10 給出了0°攻角時不同來流單位雷諾數下橢圓錐表面的TSP 實驗結果，雷諾數的變化范圍為7 × 106—1.3×107m—1.

圖10 對比了不同來流雷諾數條件下模型表面橫流影響區域溫度分布的變化，可以觀察到，在此攻角條件下，類三角形轉捩區域尖部的y坐標是大致相同的，為更清楚地反映轉捩陣面前緣的起始位置，與圖6 虛線位置對應提取了不同雷諾數時的溫升曲線，結果如圖11 所示.綜合溫升云圖與溫升曲線可以判斷，當雷諾數為7 × 106m—1時，溫度分布比較均勻，未出現高溫區域，溫升曲線整體接近于水平，未出現明顯的溫度陡升的點，判斷此時邊界層尚處于穩定的層流狀態;當雷諾數為9 ×106m—1時，在靠近模型尾部開始出現獨立的高溫區域，邊界層開始轉捩，由溫升曲線可知轉捩陣面的最前緣位于x=350 mm 左右，同時在靠近中心線兩側出現了對稱分布的細長的高溫區，可能是由橫流不穩定模態與中心線流向渦結構的相互作用引起的，具體原因還需要進一步研究;當雷諾數為1.1 × 107m—1時，轉捩陣面內溫升比雷諾數為9 ×106m—1時要高，從溫升曲線中可以印證，且此時轉捩陣面最前緣略微提前，出現在x=340 mm左右，中心線兩側的高溫區未發生明顯變化;當雷諾數升高到1.3 × 107m—1時，轉捩陣面內溫度繼續升高，轉捩陣面明顯前移，前緣出現在x=325 左右，中心線兩側的高溫區展向寬度增大，與三角形轉捩陣面連接在一起;綜上來講，橢圓錐邊界層轉捩受雷諾數的影響符合雷諾數影響轉捩的一般規律，臨界轉捩雷諾數在7 × 106m—1到9 × 106m—1，邊界層由層流開始向湍流過渡，繼續增大雷諾數時，轉捩陣面最前緣前移，轉捩提前，這是由于橫流不穩定性的本質屬于拐點不穩定性，而黏性在高超聲速條件下對邊界層起穩定作用，雷諾數增大，黏性力相對減小，導致邊界層轉捩提前.

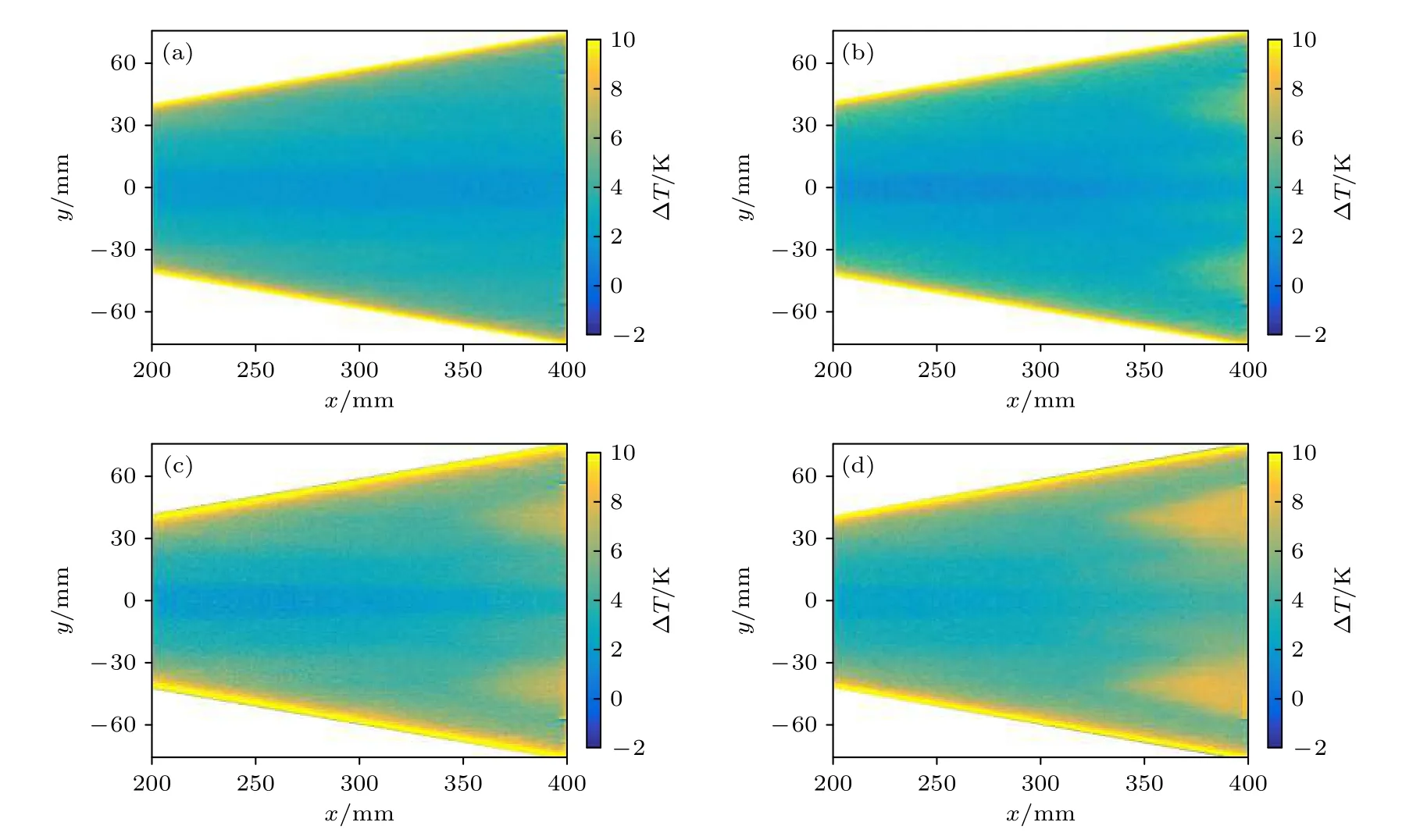
圖10 0°攻角不同雷諾數條件下TSP 圖像 (a) Re∞=7×106 m-1;(b) Re∞=9×106 m-1;(c) Re∞=1.1×107 m-1 ;(d)Re∞=1.3×107 m-1Fig.10.TSP images of angle of attack of 0° at different Reynolds numbers:(a) Re∞=7×106 m-1;(b) Re∞=9×106 m-1 ;(c) Re∞=1.1× 107m-1;(d) Re∞=1.3×107 m-1 .

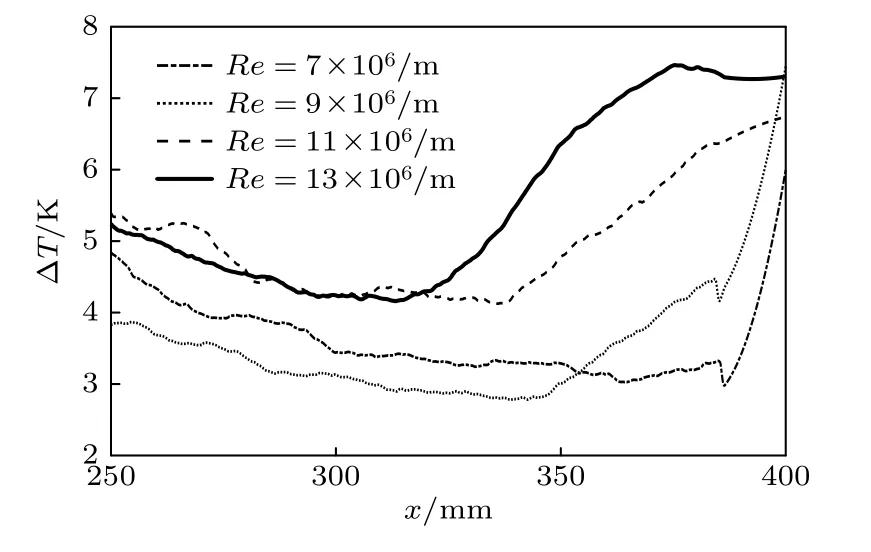
圖11 不同雷諾數條件下溫升曲線Fig.11.Temperature rise curves at different Reynolds numbers.

為研究轉捩開始出現時擾動波特征頻率的變化規律，圖12 給出了0°攻角時不同來流單位雷諾數下Kulite 壓力測試計算得到的功率譜結果，雷諾數的變化范圍為7 × 106m—1—1.3 × 107m—1.

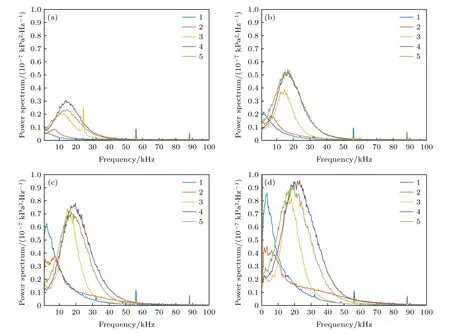
圖12 0°攻角、不同雷諾數條件下功率譜結果 (a) Re∞=7×106 m-1;(b) Re∞=9×106 m-1;(c) Re∞=1.1×107 m-1 ;(d)Re∞=1.3×107 m-1Fig.12.Power spectrum calculation results of angle of attack of 0° at different Reynolds numbers:(a) Re∞=7×106 m-1 ;(b) Re∞=9×106 m-1;(c) Re∞=1.1×107 m-1;(d) Re∞=1.3×107 m-1 .

從測點的布置和TSP 圖像的溫度分布可以看出，測點1 和測點2 對應于中心線以及中心線旁的區域，測點3—5 在可能出現轉捩的區域內.從功率譜結果可以看出，測點1 和測點2 處的峰值信號出現的位置均在10 kHz 以內，當雷諾數為7 ×106m—1和9 × 106m—1時，測點2 處峰值信號的頻率比中心線要高，隨著雷諾數的增大，測點2 處峰值信號特征頻率減小至與測點1 相同，但能量比測點1 要低，測點1 處峰值信號的能量隨雷諾數增大是逐漸增大的，說明中心線附近的橫流區域流動發生了變化，可能與中心線流向渦結構之間發生了模態間的相互作用;測點3—5 處峰值信號的頻率集中在10—20 kHz 之間，能量最高的擾動波信號出現在測點4 和測點5 附近，處于最有可能出現邊界層轉捩的區域，隨著雷諾數的增大，測點3 處的特征信號頻率從10 kHz 逐漸增加到17 kHz 左右，且幅值也是逐漸增大的，測點4 和測點5 處由15 kHz增加并穩定在20 kHz 左右，特征信號的幅值隨雷諾數增大也是逐漸增大的，可以判斷該區域內主導邊界層轉捩的橫流行進波的頻率在20 kHz左右，而橫流模態頻率與幅值隨雷諾數增大的原因可能是來流噪聲和維持可壓縮流動邊界層穩定性的黏性力減小共同造成的.

3.3 攻角對轉捩的影響

在真實的飛行條件下，飛行器的飛行姿態往往都是帶有攻角或者偏航角的，攻角的變化可能會引起飛行器表面壓力梯度的變化，進而對邊界層轉捩產生影響.對于橢圓錐模型而言，模型表面的壓力梯度方向是由兩側指向中間，在迎風面，當攻角增大時模型表面中心線附近區域的壓力會增大，使得中心線與兩側的壓力梯度減小，對邊界層轉捩造成影響.

為研究明確攻角對橢圓錐邊界層轉捩的影響規律，利用TSP 技術分別測試了當雷諾數為1.1 ×107m—1和1.3 × 107m—1時不同攻角條件下模型迎風面的溫度分布狀態，實驗結果如圖13 和圖14所示.

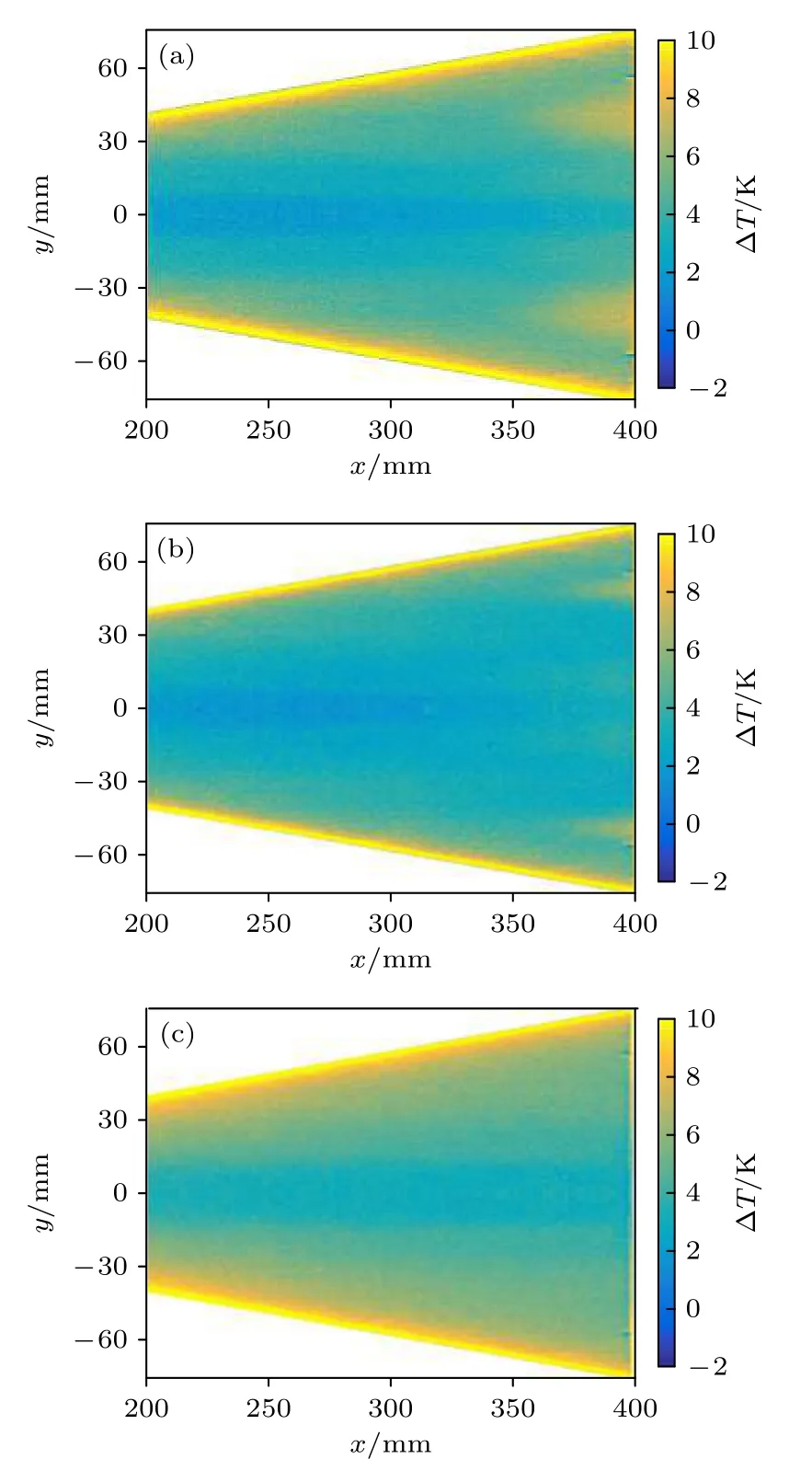
圖13 不同攻角TSP 圖像(Re∞=11×106 m-1) (a) 0°;(b) 2°;(c) 5°Fig.13.TSP images at different angles of attack (Re∞=11×106 m-1) :(a) 0°;(b) 2°;(c) 5°.

對比圖13 和圖14 可以看出，在不同的來流雷諾數條件下，攻角對模型表面邊界層的轉捩影響規律是相同的.當攻角從0°增加到2°時，中心線區域兩側細長的高溫區未發生明顯變化，說明此處的高溫區域是相對獨立的，與轉捩陣面內的高溫區域關系不大，不隨轉捩陣面的變化而變化;但攻角增大時，類似三角形的轉捩陣面變化很大，轉捩陣面前緣位置明顯推遲，且展向寬度明顯減小，轉捩區域距離中心線更遠了，這與模型表面壓力梯度的變化是對應的，說明壓力梯度變小導致橫流效應減弱，邊界層轉捩位置推遲且轉捩區域縮小;當攻角增大到5°時，模型表面的溫度分布比較均勻，無邊界層轉捩跡象.

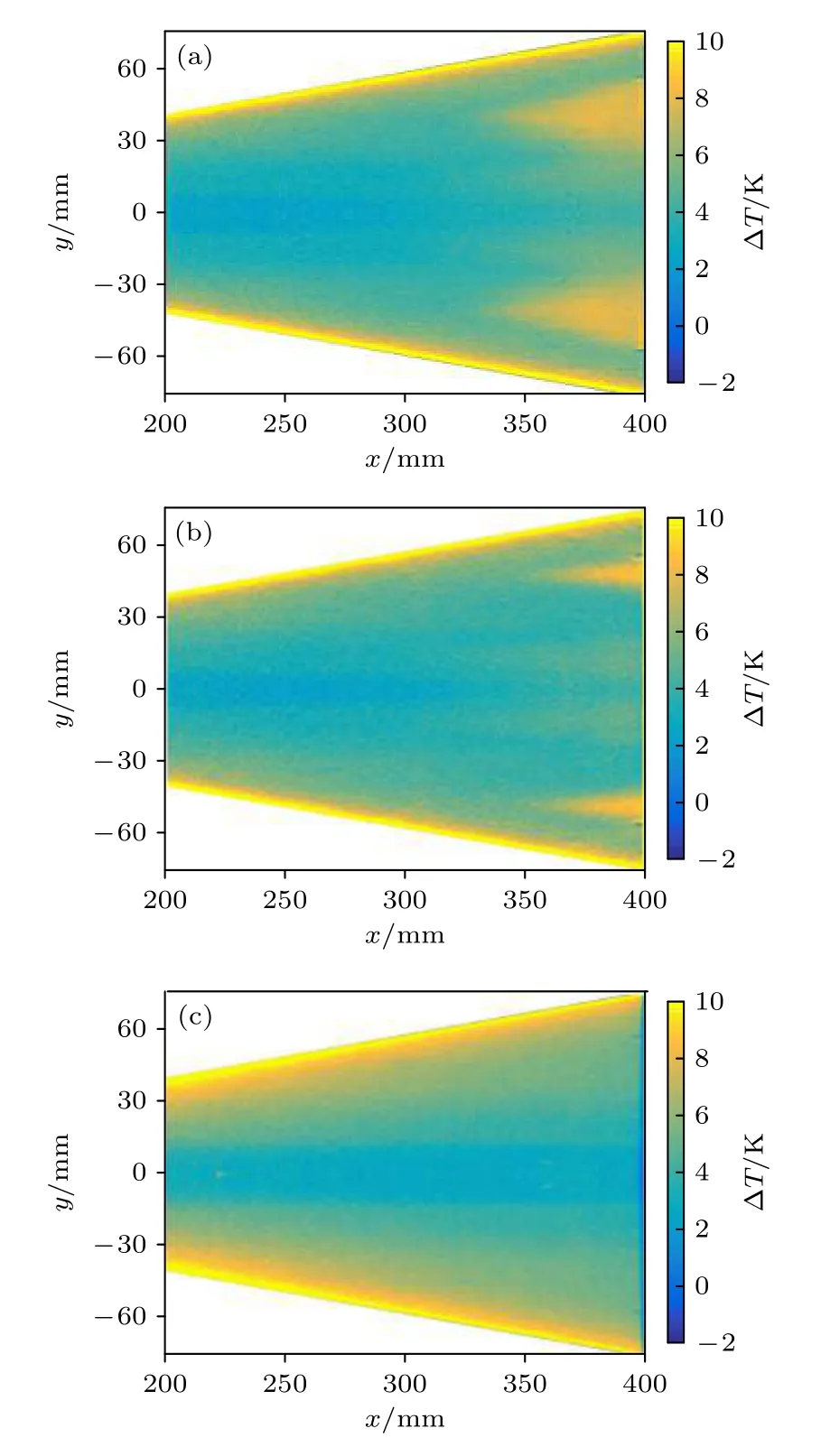
圖14 不同攻角TSP 圖像(Re∞=13×106 m-1) (a) 0°;(b) 2°;(c) 5°Fig.14.TSP images at different attack angles (Re∞=13×106 m-1):(a) 0°;(b) 2°;(c) 5°.

為研究攻角改變時模型表面邊界層內擾動波頻率的變化規律，圖15 和圖16 給出了與TSP 實驗狀態對應的Kulite 壓力測試計算得到的功率譜結果.

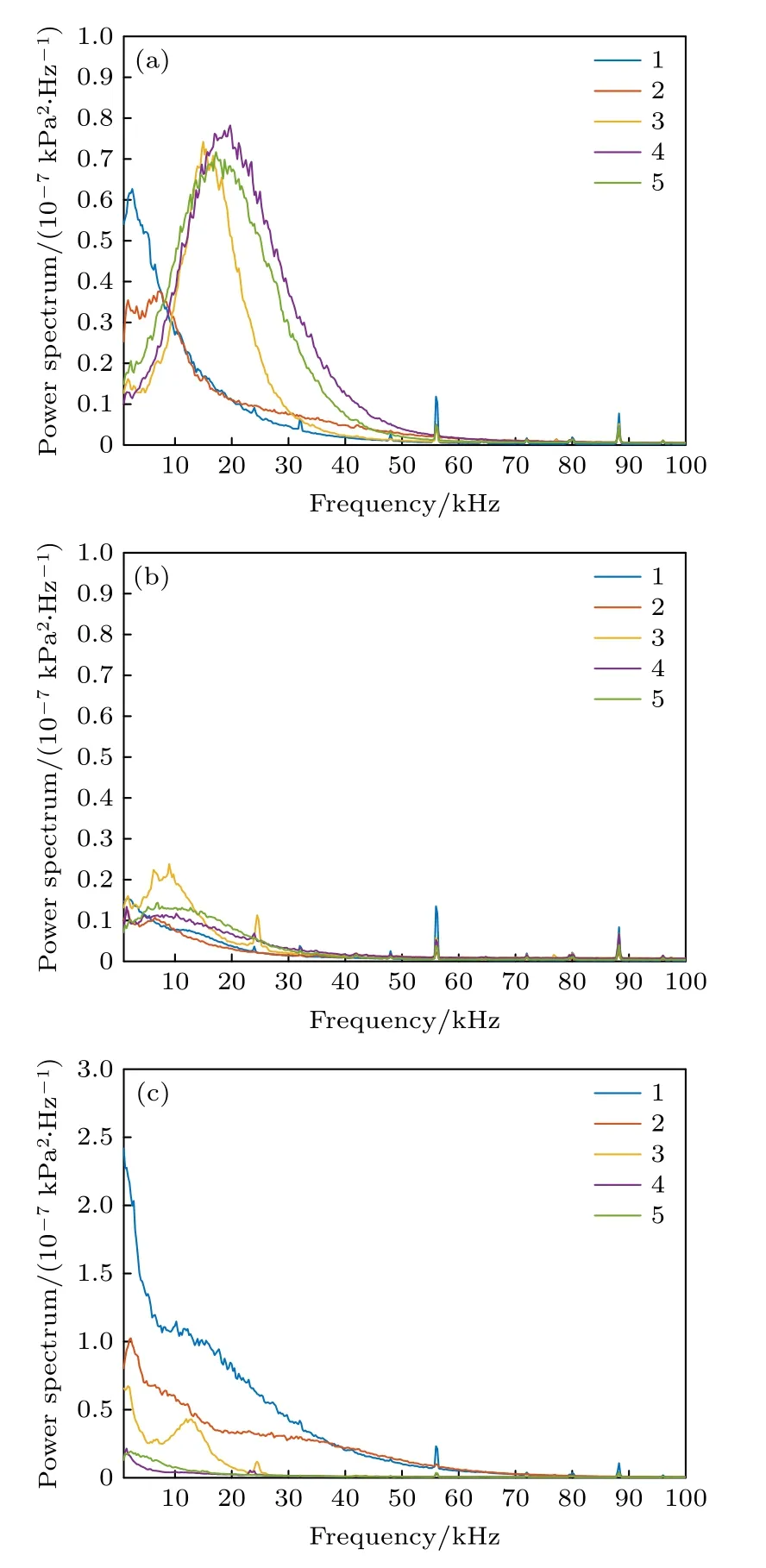
圖15 不同攻角功率譜結果(Re∞=11×106 m-1) (a) 0°;(b) 2°;(c) 5°Fig.15.Power spectrum calculation results at different angles of attack (Re∞=11×106 m-1) :(a) 0°;(b) 2°;(c) 5°.

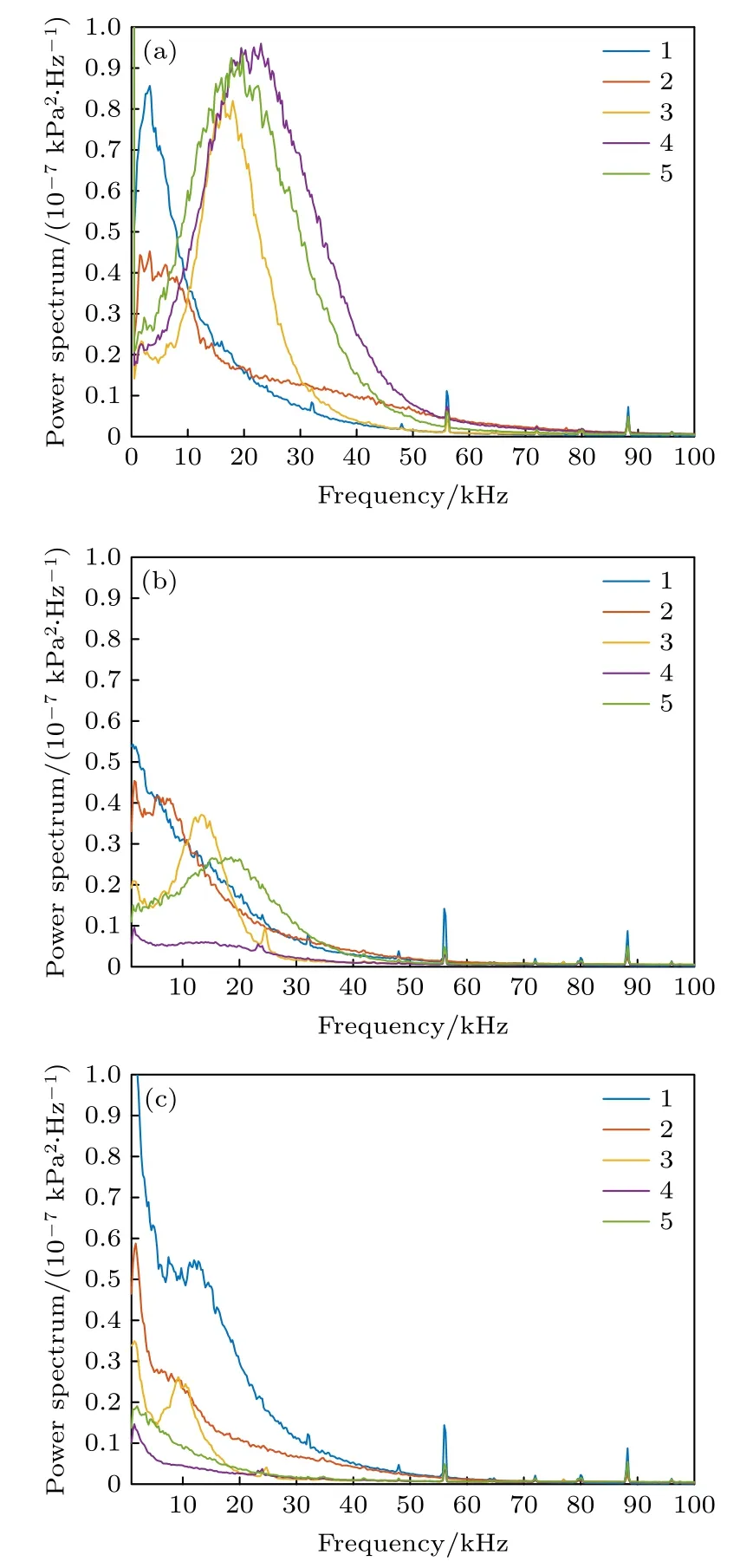
圖16 不同攻角功率譜結果(Re∞=13×106 m-1)(a) 0°;(b) 2°;(c) 5°Fig.16.Power spectrum calculation results at different angles of attack (Re∞=13×106 m-1) :(a) 0°;(b) 2°;(c) 5°.

從功率譜計算結果可以看出，在一定攻角范圍內測點1 和測點2 處峰值信號均在10 kHz 以內，且頻率保持一致，隨攻角增大幅值減小，當攻角增大至5°時不再有比較明顯的峰值信號，功率譜曲線類似于湍流的頻率曲線;對于測點3—5，當雷諾數為1.1 × 107m—1時，攻角從0°增加到2°，只有測點3 處存在明顯的峰值信號，且特征信號的頻率和幅值均減小，測點4 和測點5 未出現明顯的峰值信號，只有頻率為10 kHz 左右的主頻成分，原因是攻角為2°時兩測點不在轉捩區域內，攻角增大到5°時，測點3 處仍存在峰值信號，頻率為13 kHz左右，測點4 和測點5 處主頻成分消失;當雷諾數為1.3 × 107m—1時，攻角從0°增加到2°，測點3和測點5 處存在峰值信號，其中測點3 處特征信號的頻率和幅值均減小，測點5 頻率變化不大但幅值明顯減小，說明此時控制轉捩的行進波能量減弱，測點4 未出現明顯的主頻成分，原因是攻角為2°時測點4 不在轉捩區域內，攻角增大到5°時，測點3處仍存在峰值信號，頻率和幅值進一步減小，在10 kHz 左右，測點4 和測點5 處峰值信號和主頻成分均消失.

綜上而言，當雷諾數增大時，中心線處擾動波的頻率變化不大，中心線與轉捩區之間的范圍內，始終存在著頻率為10—15 kHz 的擾動波信號，說明攻角增大時，中心線與前緣線中間區域的橫流效應不會完全消失，橫流的行進波始終存在但無法引起轉捩，而對于起主導作用的20 kHz 左右的行進波，隨攻角的增大行進波的能量也會減弱.

4 結論

本文基于TSP 技術、NPLS 技術以及Kulite壓力測試的實驗結果，綜合分析了長短軸比為4∶1的橢圓錐表面橫流不穩定控制轉捩的機理，得到了來流單位雷諾數以及攻角對邊界層轉捩的影響規律.結果表明，在噪聲模式下，對于長短軸比為4∶1 的鈍頭橢圓錐，中心線與前緣線之間的區域是由橫流的行進波占主導的，未觀察到橫流定常渦的足跡，行進波的特征頻率頻率大約為20 kHz，轉捩陣面為沿中心線對稱分布的兩個類似三角形的形狀;當雷諾數增大時，轉捩陣面前緣前移，邊界層轉捩位置提前，行進波的頻率和幅值均增大;在一定的攻角范圍內，當攻角增大時，迎風面轉捩陣面前緣位置推遲且轉捩陣面的展向寬度減小，這與模型表面壓力梯度減小有關，引起轉捩的行進波的頻率變化不大但擾動波的能量會減小;當攻角繼續增大時，轉捩陣面會消失，但此時模型表面仍存在橫流效應，但已不能控制和引起邊界層轉捩.