基于分層貝葉斯模型的齒輪彎曲疲勞試驗分析

毛天雨 劉懷舉 王寶賓 侯圣文 陳地發

1.重慶大學機械傳動國家重點實驗室，重慶，4000442.陜西法士特齒輪有限責任公司，西安，710077

0 引言

齒輪廣泛應用于航空、航天、艦船、高鐵、海洋裝備等領域，其服役性能直接決定了整機裝備的可靠性[1]，而且齒輪彎曲疲勞失效導致的裝備事故和人機安全問題日益突出[2]，因此開展齒輪彎曲疲勞試驗非常必要。以試驗基礎數據為主要支撐是進行高可靠齒輪設計的必要前提，同時也是對齒輪疲勞壽命等服役性能最為直接和有效的評估手段。

齒輪彎曲疲勞試驗基礎數據一般指可靠度-應力-壽命(P-S-N)曲線，它也是齒輪疲勞強度設計的基本參數。獲取P-S-N曲線通常采用成組法，在4～5個應力級下進行試驗，每個應力級下不少于5個試驗點[3]。但由于齒輪彎曲疲勞試驗結果受齒輪材料微結構特征、加工工藝、表面質量等多種不確定性因素的影響，試驗壽命數據分散明顯，一般情況下難以獲得滿足傳統統計方法所需要的大樣本數據。目前小樣本疲勞試驗數據的分析方法，一類是通過改進大樣本統計方法，如傅慧民等[4]在假設疲勞壽命服從對數正態分布的前提下，采用異方差回歸分析的方法對疲勞試驗數據進行整體分析；XIE等[5]提出了一種基于樣本信息聚集原理的P-S-N曲線數據處理方法，通過將在不同應力水平下測試的疲勞壽命轉換成在任意應力水平下的等效壽命，將小樣本數據轉換為大規模樣本；GAO等[6]基于P-S-N曲線在高應力區某一點相交的假設，實現了P-S-N曲線的快速獲取。另一類是通過樣本擴充，使之盡可能適應大樣本數據統計方法。如馬宇鵬等[7]提出了Bootstrap-支持向量回歸-二階累次量的方法框架和多階虛擬樣本容量擴充的方法，解決了小樣本分析的問題；趙遠等[8]基于Bootstrap法充分挖掘試驗數據的壽命與可靠性總體信息，提高了小子樣數據評估的準確性。然而樣本數據擴充方法的本質依然是進行頻率統計，當樣本量較小時，進行樣本擴充可能會產生誤差。另外，傳統的概率方法往往需要大量的疲勞試驗數據作為依托，而齒輪疲勞試驗耗時耗力，商用諧振式高頻疲勞試驗機加載頻率一般為50～100 Hz，依據ISO 6336標準規定的3×106次循環基數，一個試驗點要進行17 h(按50 Hz計算)的試驗，這導致通常可用于分析的疲勞試驗數據往往是小樣本的，而貝葉斯統計方法可用于推斷疲勞測試數據并處理不確定性，可通過不斷更新和融合數據來解決樣本量較少這一問題。GUIDA等[9]借助貝葉斯理論和先驗信息，將材料疲勞性能參數引入先驗分布中，發現無論是點估計還是區間估計，所提出的貝葉斯方法遠優于經典頻率理論方法；劉建中等[10]運用模糊綜合評判方法綜合經驗信息來確定先驗分布，同時基于貝葉斯理論給出了一種由小樣本試驗數據確定疲勞壽命分布的可靠方法。然而，上述方法均是采用經驗貝葉斯方法，其先驗分布的選取易受到主觀信息的影響，在缺乏先驗信息的情況下往往存在爭議。而分層貝葉斯可以避免超參數的選取，能夠提供一種更具魯棒性的統計分析手段[11]。

本文開展了8620H鋼表面滲碳齒輪彎曲疲勞試驗，并針對傳統統計方法處理小樣本齒輪彎曲疲勞試驗數據擬合失真的問題，基于貝葉斯理論建立了齒輪彎曲疲勞P-S-N曲線的分層貝葉斯模型，給出了在無先驗信息下分布參數的選取方法，通過Gibbs采樣對模型進行求解并獲取模型參數的后驗分布。結合齒輪彎曲疲勞試驗數據，以50%和99%可靠度下S-N曲線相對斜率比為擬合結果評價指標，驗證了分層貝葉斯模型在小樣本數據下的穩定性與優越性。

1 齒輪彎曲疲勞試驗

輪齒彎曲疲勞破壞是齒輪最嚴重的失效形式之一，航空齒輪的斷齒甚至還會導致機毀人亡的慘劇[12]，因此，將齒輪彎曲疲勞失效作為研究對象，通過試驗獲得齒輪的彎曲疲勞壽命數據與齒輪彎曲疲勞P-S-N曲線，對指導高性能齒輪正向設計具有顯著的工程意義。

1.1 齒輪試樣

齒輪試樣參數如表1所示，制造工藝路線為：毛坯鍛造→粗車→半精車與精車→滾齒→滲碳淬火→磨齒。所有試驗齒輪均采用相同的加工設備及加工工藝，且在同一爐進行熱處理。

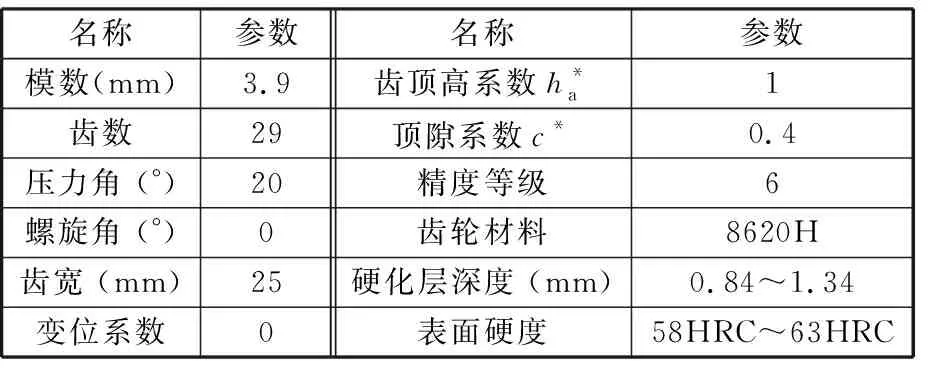
表1 試驗齒輪基本參數

1.2 試驗方法

齒輪彎曲疲勞試驗通常采用脈動加載方式[13]，通過疲勞試驗機上的夾具對試驗齒輪輪齒進行脈動加載，直至輪齒發生彎曲疲勞失效或越出(循環基數通常為3×106)。試驗中，脈動載荷僅施加在試驗齒輪輪齒上，試驗齒輪不做嚙合運轉。

成組法是齒輪彎曲疲勞試驗中的常用方法，該方法通過在4～5個應力級下進行多組壽命測試來獲得齒輪在各個應力級下的壽命分布，進而獲得齒輪的彎曲疲勞P-S-N曲線。圖1為P-S-N曲線示意圖，分別代表了1%、50%、99%可靠度下的S-N曲線。

1.3 試驗設備

試驗采用Zwick 1000 kN彎曲疲勞試驗機和 GB/T 14230—1993標準[14]中脈動加載的形式，對試驗齒輪進行脈動循環加載，以獲得某恒定載荷級下的齒輪彎曲疲勞壽命。彎曲疲勞試驗機基本參數如表2所示，齒輪彎曲疲勞試驗現場如圖2所示。

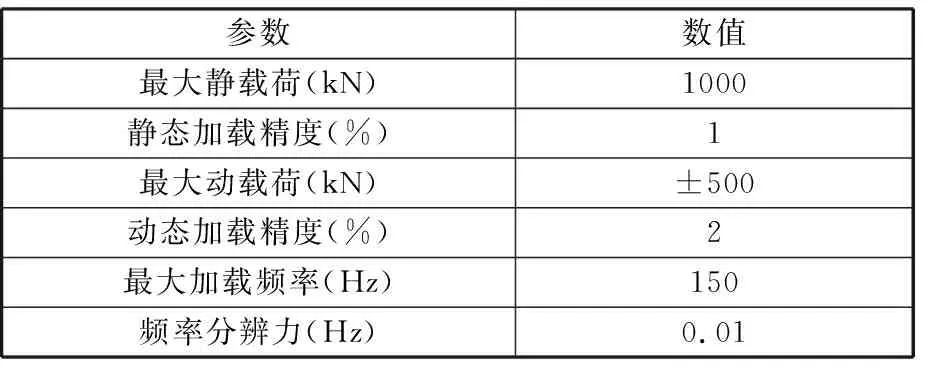
表2 彎曲疲勞試驗機基本參數

圖2 齒輪彎曲疲勞試驗Fig.2 Gear bending fatigue test

1.4 齒輪失效的檢測與判據

試驗過程中，疲勞試驗機通過脈動循環加載與齒輪發生共振，其共振頻率和疲勞試驗機與齒輪組成的總剛度和質量有關[15]。當齒輪出現裂紋后，系統剛度減小，從而引起頻率的下降。根據GB/T 14230—1993標準[14]的要求，當滿足以下兩者之一的條件即可判定齒輪發生失效：①出現可見裂紋或斷齒；②頻率下降5%～10%。

1.5 試驗數據的預處理

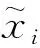
(1)

水邊植物群落和建筑周邊植物群落在各指標上都有一定程度的下降,根據駁岸類型和與建筑的位置關系進一步分析(圖6)。

2 試驗數據處理方法

齒輪彎曲疲勞試驗數據常用的統計方法有正態分布、對數正態分布、雙參數威布爾分布和三參數威布爾分布[19]。由于模型可及性和許多計算工具易于找到，對數正態分布在疲勞試驗數據處理中被廣泛使用[20-21]，因此，在本文數據處理中，采用對數正態分布擬合，通過成組法數據確定疲勞曲線的有限壽命階段，即齒輪的P-S-N曲線方程。

2.1 基于頻率理論的P-S-N曲線擬合

在有限壽命階段，可靠度P下的失效循環次數NP與應力S滿足Basquin方程[22]：

SmPNP=CP

(2)

式中，mP、CP為材料參數，mP>0，CP>0。

通過對式(2)左右兩邊取對數，可以得到線性表達式：

lgNP=lgCP-mPlgS

(3)

由式(3)可以看出，Basquin方程在雙對數坐標下呈現出線性關系。

如圖3所示，獲取齒輪彎曲疲勞P-S-N曲線，首先需要確定各應力水平下的疲勞壽命分布，其次需要確定各應力水平下可靠度P下的疲勞壽命NP，進而通過最小二乘法(least squares method，LSE)對式(3)進行擬合以獲取P-S-N曲線，具體計算流程可參考GB/T 14230—1993標準[14]。

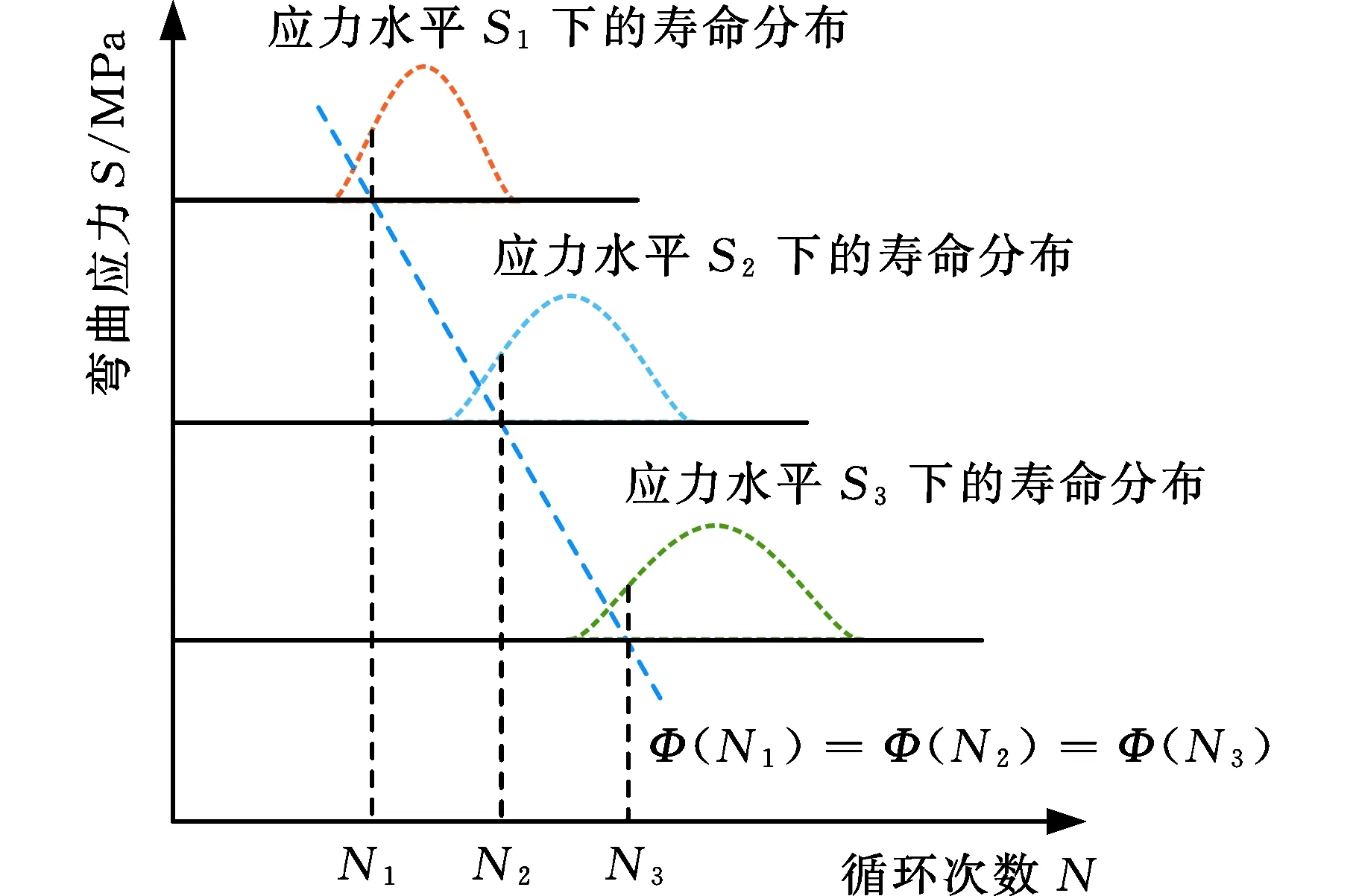
圖3 P-S-N曲線擬合原理圖Fig.3 P-S-N curve fitting principle diagram

2.2 基于分層貝葉斯模型的P-S-N曲線擬合

從貝葉斯統計的觀點來看，模型參數也被看作是具有概率分布的隨機變量[23]。分層貝葉斯方法(hierarchical Bayesian model，HBM)相對于經驗貝葉斯方法的優勢在于分層先驗中包含了模型參數的結構信息[24]，同時避免了超參數的選擇，能夠提供一種更具魯棒性的分析手段。本文將齒輪彎曲疲勞壽命數據建模分為兩個層次，如圖4所示，一個層次是指每個應力水平下的疲勞壽命，另一個層次是不同的應力水平下的疲勞壽命。HBM模型將各應力級下疲勞壽命參數分布估計與S-N曲線的線性擬合同時進行，并將計算應力水平之外的疲勞壽命分布信息考慮在內，以進行數據的融合與交換，從而獲取最優擬合結果。

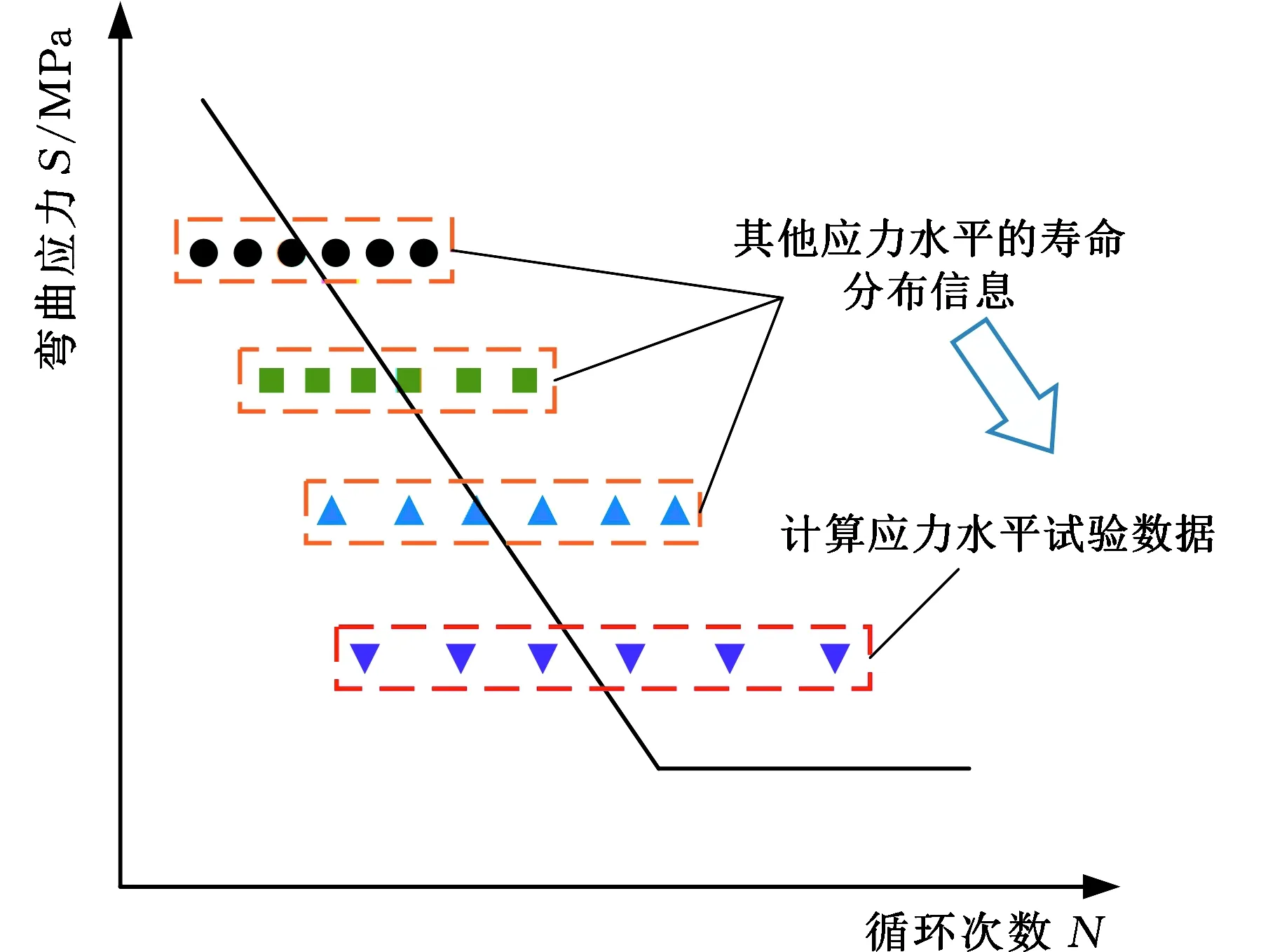
圖4 分層貝葉斯模型估計S-N曲線示意圖Fig.4 Schematic diagram of S-N curve estimated byhierarchical Bayesian model

本文中齒輪彎曲疲勞S-N曲線采用目前最為常用的Basquin模型，若考慮各應力水平下疲勞壽命的隨機性，則Basquin方程可表達為

(4)

其中，m、C為材料參數；Nj、Sj分別為第j個應力水平下疲勞壽命與應力(j=1,2,…，n;n為應力水平數)；隨機變量εj表示在不同應力水平Sj下的隨機性，包含材料疲勞特性的不確定性與觀測誤差。兩邊同時取對數，可得

lgNj=lgC-mlgSj+δj

(5)

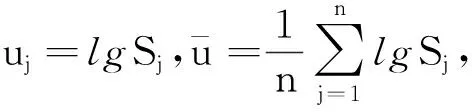
Yj=Xjβ+δj

(6)

Yj=lgNjXj=(1,lgxj)β=(β0,β1)T

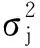
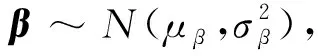
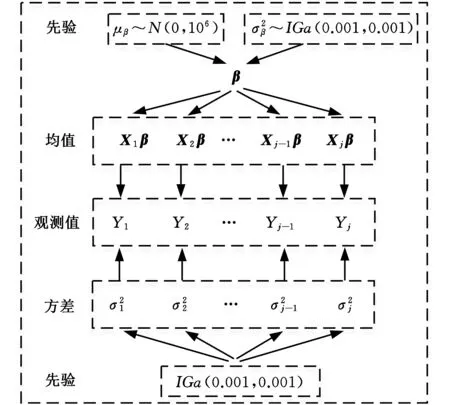
圖5 分層貝葉斯層次結構圖Fig.5 Hierarchical Bayesian hierarchy diagram

后驗分布的計算通常采用數值積分方法求解，馬爾可夫鏈蒙特卡羅(Markov chain Monte Carlo，MCMC)抽樣技術[29]中的Gibbs抽樣算法適合分層貝葉斯模型，能有效解決高維積分問題[30]，因此本文采用Gibbs抽樣算法來求解后驗分布。

在樣本量較少的情況下，可能存在低應力水平下對數疲勞壽命標準差比高應力水平下對數疲勞壽命標準差小的情形，與目前普遍認為的異方差或同方差理論相悖[31-32]。考慮到本試驗中齒輪來自于相同的材料與熱處理加工工藝，將不同應力水平下的疲勞壽命分散性用統一的變異系數來度量，以此來表征齒輪材料及加工工藝的一致性。統一的變異系數為

(7)

從而各應力水平下壽命分布的方差可調整為

(8)

2.3 模型的比較與驗證

為了驗證HBM模型估計P-S-N曲線的性能，將HBM模型與傳統LSE模型進行穩定性比較。本節提出了相對斜率指標來進行模型穩定性的比較。假設b0.5表示可靠度為50%下S-N曲線的斜率，b0.99表示可靠度為99%下S-N曲線的斜率，則相對斜率比指標可定義為

(9)

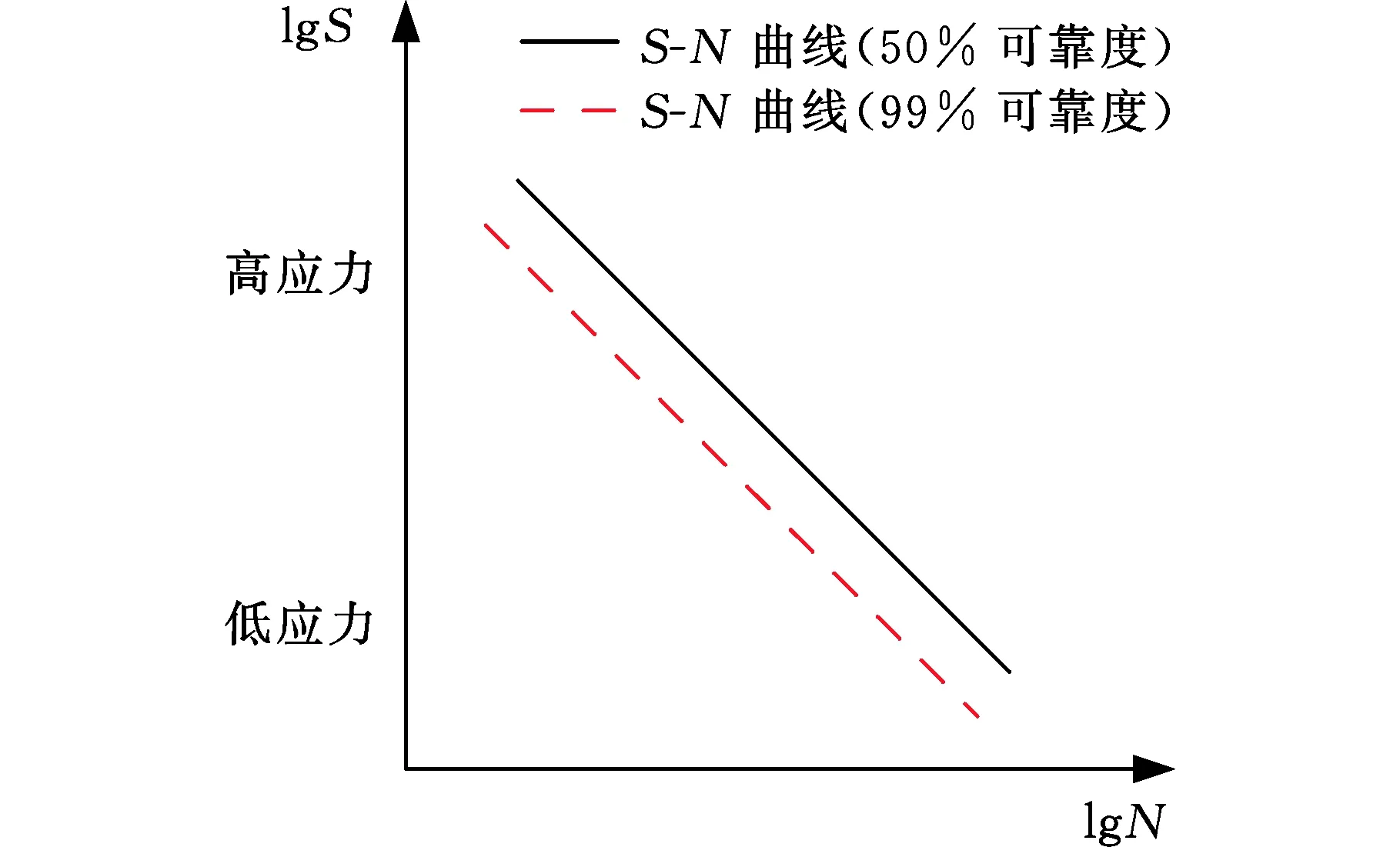
(a)α=1

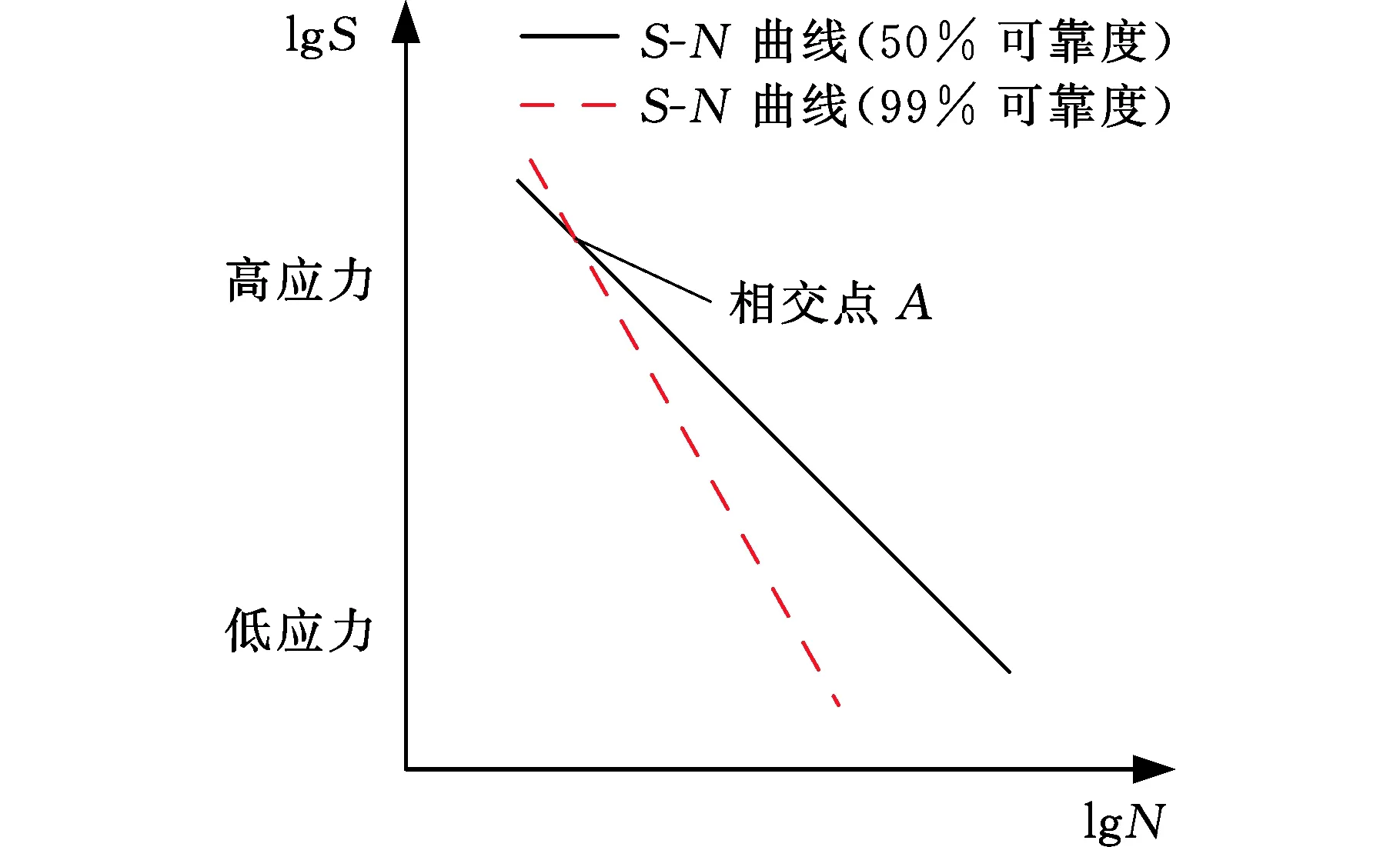
(b)α>1

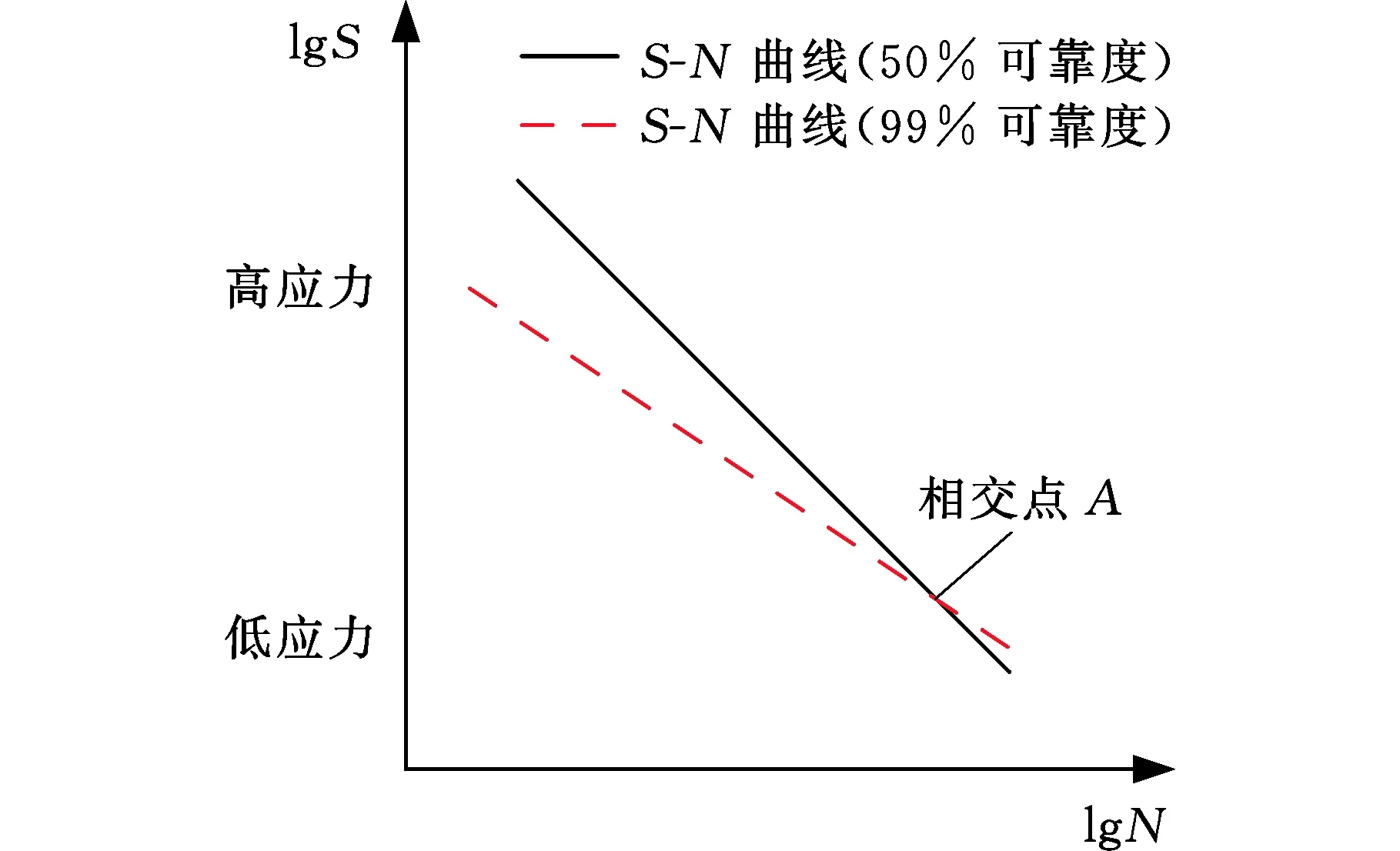
(c)α<1圖6 99%可靠度與50%可靠度下S-N曲線的相對位置關系示意圖Fig.6 Schematic diagram of the relative positionrelationship of the S-N curve under 99%reliability and 50% reliability

式(9)中的相對斜率比α描述了50%可靠度下與99%可靠度下S-N曲線的相對位置關系，如圖6所示。當相對斜率比α=1時，99%可靠度下S-N曲線與50%可靠度下S-N曲線平行，如圖6a所示；當相對斜率比α>1時，99%可靠度下S-N曲線與50%可靠度下S-N曲線相交于高應力級下的一點，如圖6b所示，該點代表該應力級下試件必定會發生疲勞失效，這與高應力級下易發生彎曲疲勞失效的事實一致；當相對斜率比α<1時，99%可靠度下S-N曲線與50%可靠度下S-N曲線相交于低應力級下的一點，如圖6c所示，顯然，這與較低應力下存在越出點的事實是相悖的。此時，P-S-N曲線擬合出現失真。因此，可以接受α≥1的情況而不能接受α<1的情況。

3 結果與討論

本文采用的齒輪彎曲疲勞試驗數據，是在4個應力水平(該齒輪彎曲疲勞強度極限約為665 MPa)下進行試驗獲得的數據，每組試驗11次，試驗結果見表3。每組11個試驗點提供了足夠的數據量以作為評價小樣本條件下擬合效果的基準。

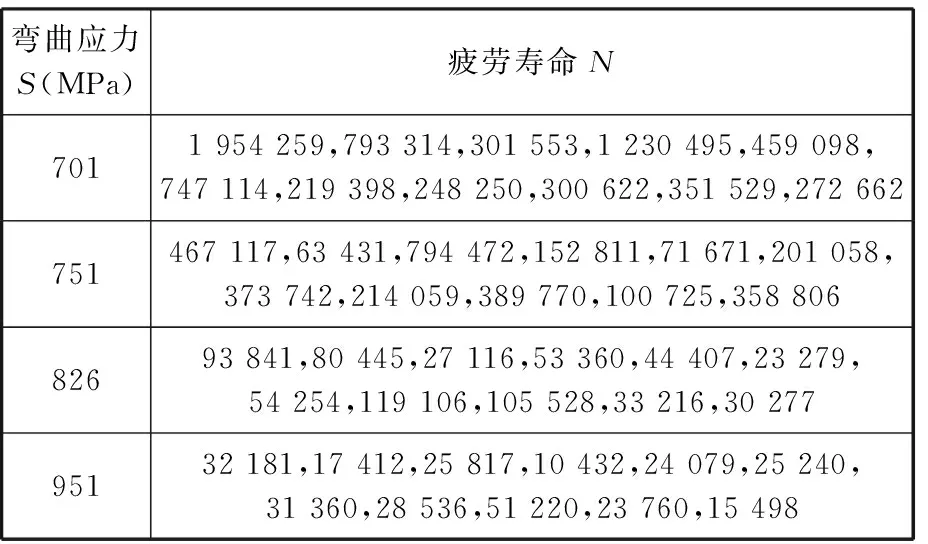
表3 齒輪彎曲疲勞試驗結果

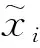
對于“11-11-11-11”(即4個應力級下11個試驗點)樣本，LSE模型已被證明在大樣本情況下有效，因此將其所獲得的結果作為基準曲線。由圖7a可以看出，HBM模型獲得的S-N曲線與LSE模型獲得的S-N曲線幾乎重合。以相同應力水平下LSE模型的疲勞壽命作為基準，絕對誤差計算結果如圖7b所示，四個應力級下擬合壽命最大誤差為6.10%，表明本文所提出的HBM模型在“大樣本數據”情況下具有與LSE模型相同的建模精度。

為對比本文所提出的HBM模型與傳統LSE模型統計的穩定性，將疲勞試驗數據分為“3-3-3-3”、“5-5-5-5”、“7-7-7-7”、“9-9-9-9”四種樣本。在每種測試方案下，用于比較的子數據集都是從表3中完整的數據中進行隨機抽樣的，每個測試方案下隨機抽樣104次，表5給出了不同樣本量下的統計結果，可以看出，在不同樣本量下，本文所提出的HBM模型的相對斜率比α均能給出滿意的結果，而傳統的LSE模型會出現P-S-N曲線擬合失真的情況。這是因為當疲勞壽命數據不滿足隨著應力水平逐漸降低而疲勞壽命方差逐漸增大的規律時，傳統的LSE模型不能給出滿意的擬合結果，而本文所提出的模型穩定性更好而不依賴于數據樣本本身。

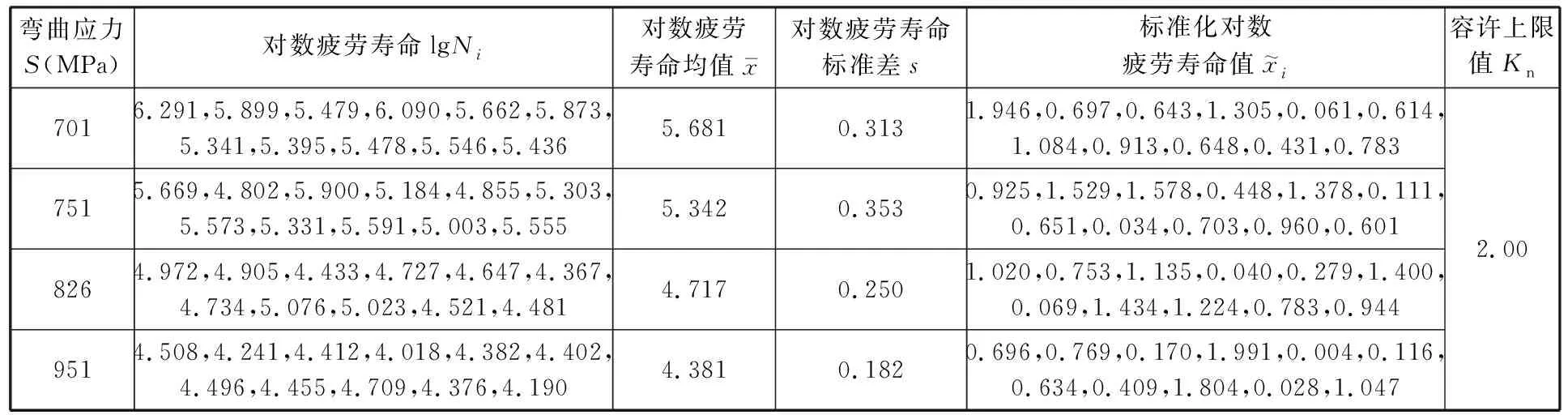
表4 齒輪彎曲疲勞試驗數據預處理

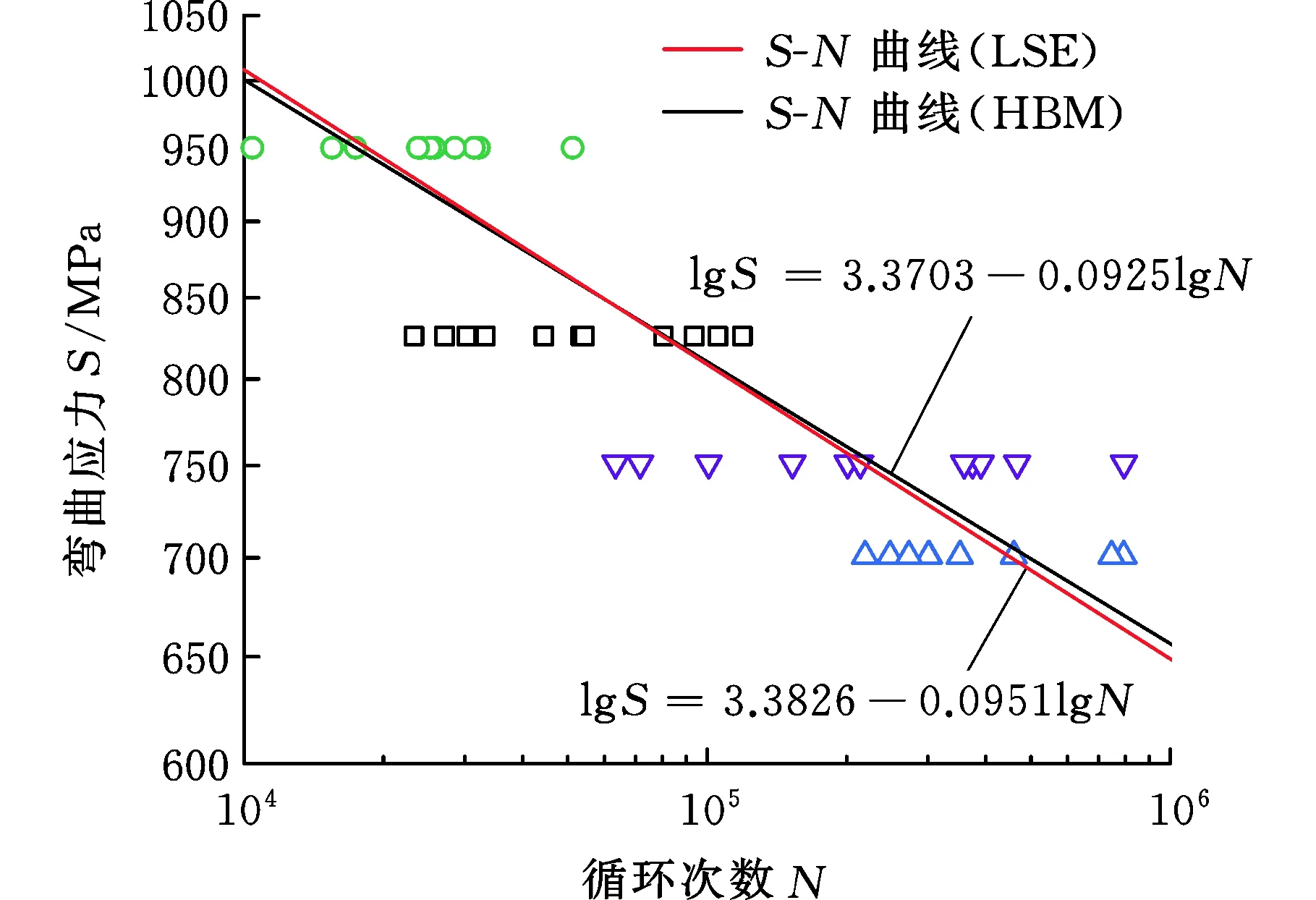
(a)50%可靠度下S-N曲線

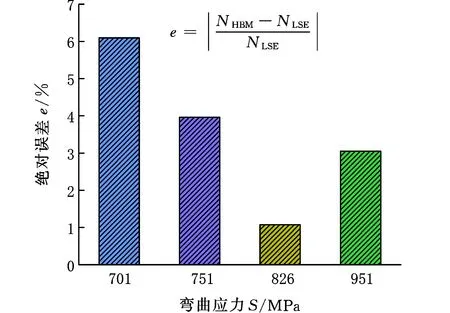
(b)擬合壽命絕對誤差圖7 11-11-11-11樣本量下50%可靠度下S-N曲線與每個應力水平壽命的誤差Fig.7 The error between the S-N curve and the lifeof each stress level at 50% reliability under 11-11-11-11sample size

其次，LSE與HBM模型相對斜率比α波動范圍均隨樣本量增加而減小，但本文所提出的HBM模型波動范圍較小。隨著樣本量的變化，LSE模型最小波動范圍為0.7869，是本文所提出的HBM模型最大波動范圍(即0.2213，樣本量為“3-3-3-3”)的3.6倍左右。顯然，與傳統的LSE模型相比，本文所提出的HBM模型具有更好的穩定性。

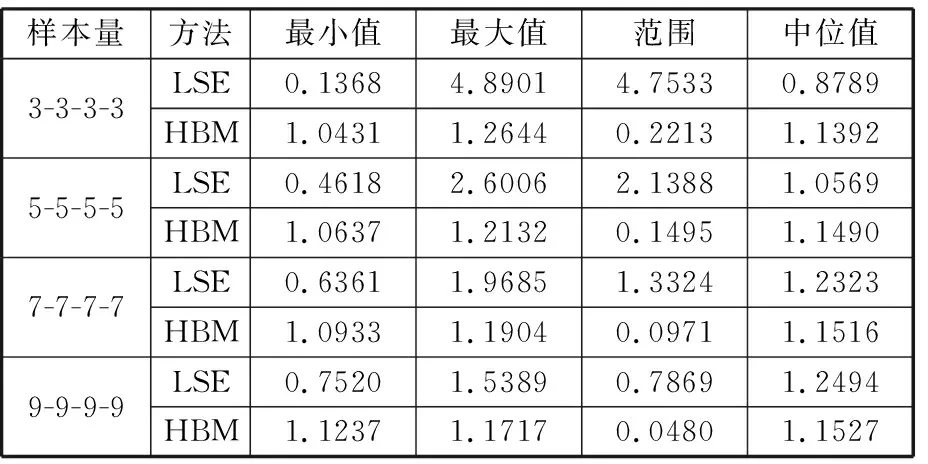
表5 不同樣本量下的相對斜率比α值

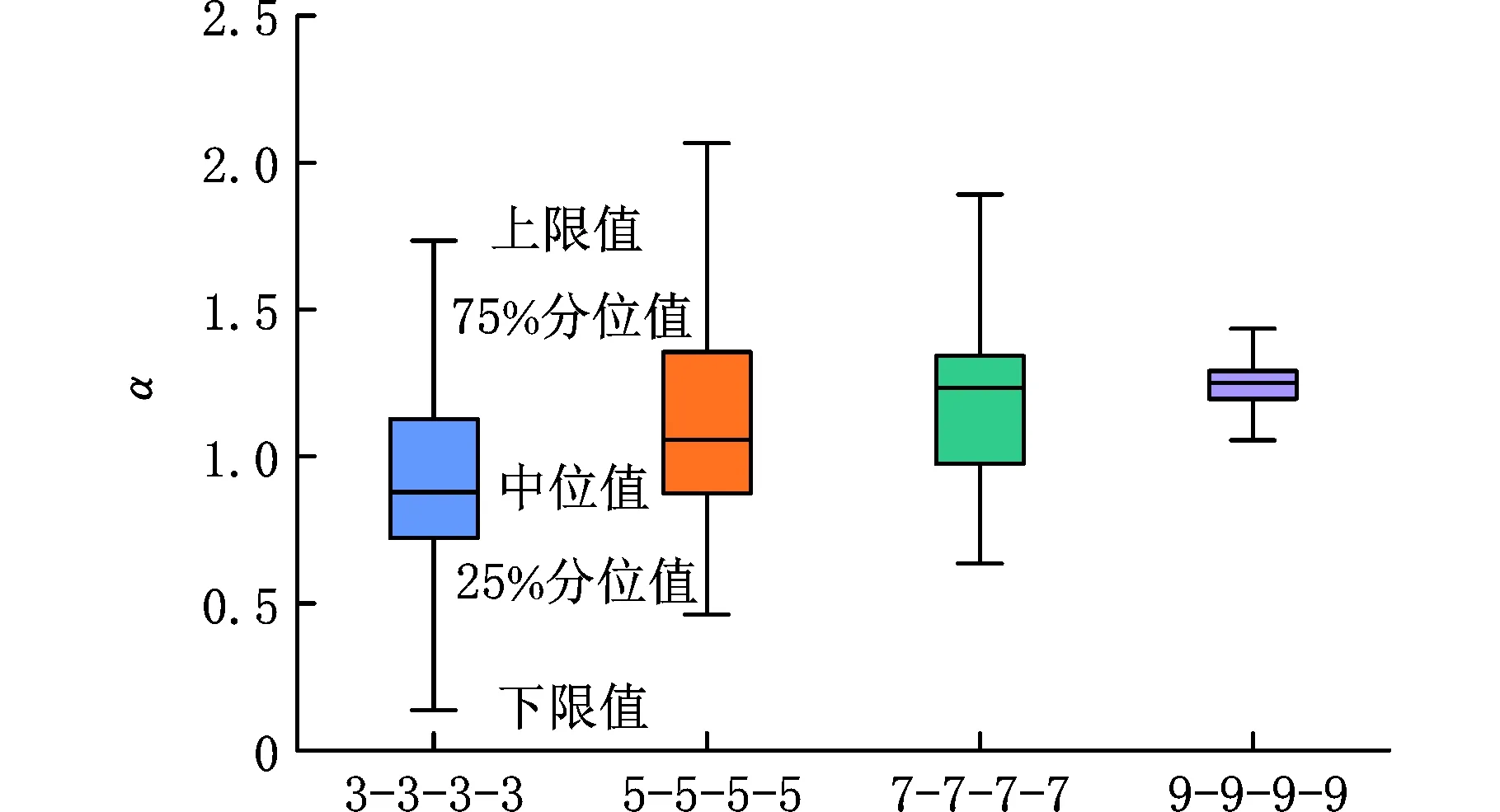
(a)不同樣本量下LSE模型α值

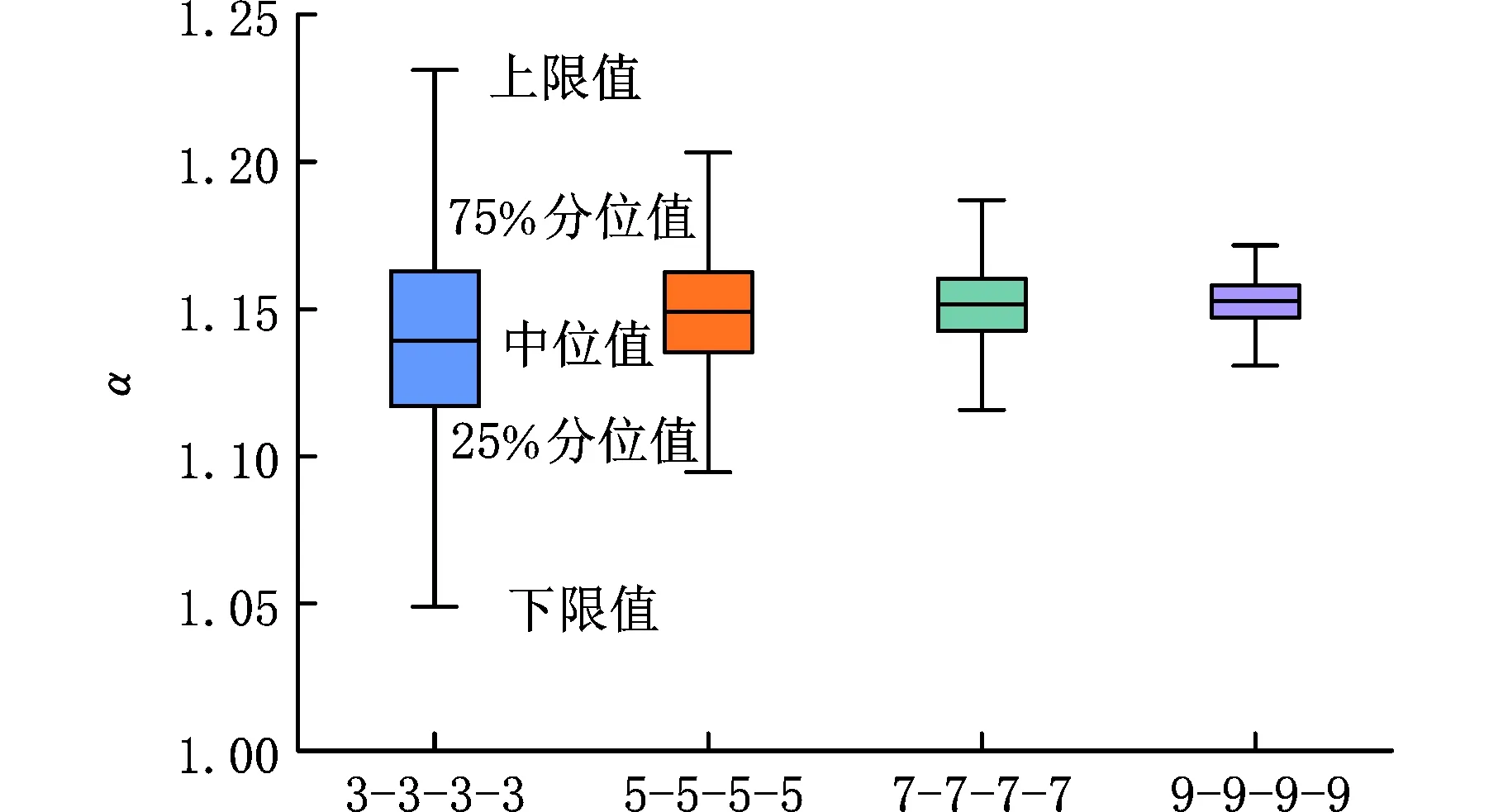
(b)不同樣本量下HBM模型α值圖8 不同樣本量下LSE與HBM模型α值Fig.8 LSE and HBM model α values under differentsample sizes

由圖8a和圖8b中的箱型圖可以看出，隨著樣本量的變化下，本文提出的HBM模型相對斜率比α均大于1，而LSE模型在樣本量為“3-3-3-3”和“5-5-5-5”時易出現擬合失真的情況。當樣本量從“3-3-3-3”增加到“9-9-9-9”時，HBM模型相對斜率比α的中位值從1.1392增大到1.1527，變化率為1.19%；而LSE模型中位值從0.8789增大到1.2494，變化率為42.14%。結合目前彎曲疲勞試驗數據可知，本文所提出的HBM模型在小樣本下擬合效果更佳，不會出現擬合失真的情況。

4 結論

本文開展了齒輪彎曲疲勞試驗，并基于齒輪疲勞試驗結果提出了用于估計齒輪彎曲疲勞P-S-N曲線的分層貝葉斯(HBM)模型，通過馬爾可夫鏈蒙特卡羅(MCMC)數值仿真得出以下結論：

(1)采用單齒加載方式進行齒輪彎曲疲勞試驗，獲得了8620H鋼滲碳齒輪材料在701 MPa、751 MPa、826 MPa、951 MPa四個彎曲應力級下的彎曲疲勞壽命數據，并建立了HBM模型與LSE模型進行疲勞試驗數據的分析與處理。

(2)定義了用于評價P-S-N曲線擬合精度的相對斜率比指標。發現在大樣本情況下，HBM模型具有與傳統LSE模型相同的建模精度。隨著樣本量的變化，LSE模型相對斜率比α變化率為42.14%，而本文所提出的HBM模型變化率僅為1.19%，具有更好的穩定性與適應性，為齒輪彎曲疲勞試驗等小樣本數據場合提供了更具魯棒性的分析手段。