同軸等大圓線圈互感系數的測量

隗群梅

摘? 要：同軸線圈的互感系數與其相互作用能和相互作用力密切相關，是物理學的基礎理論問題，也具有工程應用價值。該文采用LCR數字電橋先測量線圈N1和N2的自感LN1和LN2;然后根據自感和互感的關系，得到不同距離處的互感系數M;最后利用Origin8.0強大的數據處理功能模擬出互感系數與相對位置之間的關系表達式，實驗數據曲線與擬合曲線擬合系數達到99%以上，與理論積分近似計算的結果表述一致。實驗測量互感的方法可以減少繁瑣的積分計算，也可以得到互感系數與相對位置之間的函數關系。

關鍵詞：LCR數字電橋 自感 互感系數 Origin程序 相對位置

中圖分類號：O441 文獻標識碼：A? ?文章編號：1672-3791（2021）10（b）-0000-00

Mutual Inductance Measurement of Coaxial and Large Round Coils

WEI Qunmei

（College of Science， China University of Petroleum （east China）， Qingdao， Shandong Province， 266580 China）

Abstract： The mutual inductance of the T coaxial coil is closely related to its interaction energy and force. It is a basic theoretical problem of physics and has engineering application value. In this paper， the LCR digital bridge is used to measure the self-inductances LN1 and LN2 of the coils N1 and N2; then， according to the relationship between self-inductance and mutual inductance， the mutual inductance coefficient M at different distances is obtained; finally， the powerful data processing function of Origin8.0 is used to simulate the mutual inductance The relationship expression between the coefficient and the relative position， the fitting coefficient of the experimental data curve and the fitting curve reaches more than 99%， which is consistent with the result of the theoretical integral approximate calculation. The method of experimental measurement of mutual inductance can reduce the tedious integral calculation， and can also obtain the functional relationship between the mutual inductance coefficient and the relative position.

Key Words： LCR digital bridge;Self-inductance; Mutual inductance coefficient; Origin program; Relative position

兩個同軸圓線圈互感系數是電磁學的基礎理論問題之一，在理論上進行推導時都需要進行適當的近似或猜想才能得出近似的解析公式[1-4]，且其在進行計算時一般都比較復雜，因此常用實驗的方法進行測定[5-6]。下面根據電感和互感的關系，得出互感系數的表達式，從表達式中可以看出，只需要借用現在功能全、測量精度高的LCR電橋測量自感和互感系數[7]，就可以得到互感系數與線圈距離數據關系，再利用Origin8.0[8]強大的數據處理功能建立兩固定線圈的互感系數與其相對位置的關系表達式，并與參考文獻[1-3]中理論計算比較，得出實驗測量得到的解析式與理論計算的結果變化規律一致，且數據曲線與擬合曲線的擬合系數達到99%以上。由此可見實驗測量互感系數的也可以被工程技術所運用。

1 兩線圈互感系數M的測量原理

根據電感和互感的關系，可根據同名端的順向串聯和反向串聯值計算得到互感值。設線圈N1、N2對應的自感為LN1、LN2，則順向串聯的電感值L1=LN1+LN2+2M。反向串聯時電感值L2= LN1+LN2-2M。從而可得到

M=1/4 |L_1-L_2 | （1）

對于鐵芯線圈，耦合程度緊密，所以M值相對比較大;對于兩個空心線圈，互感系數只與兩個線圈回路本身結構和相對位置有關，而與電流無關[9]。

2 判斷互感線圈同名端的方法

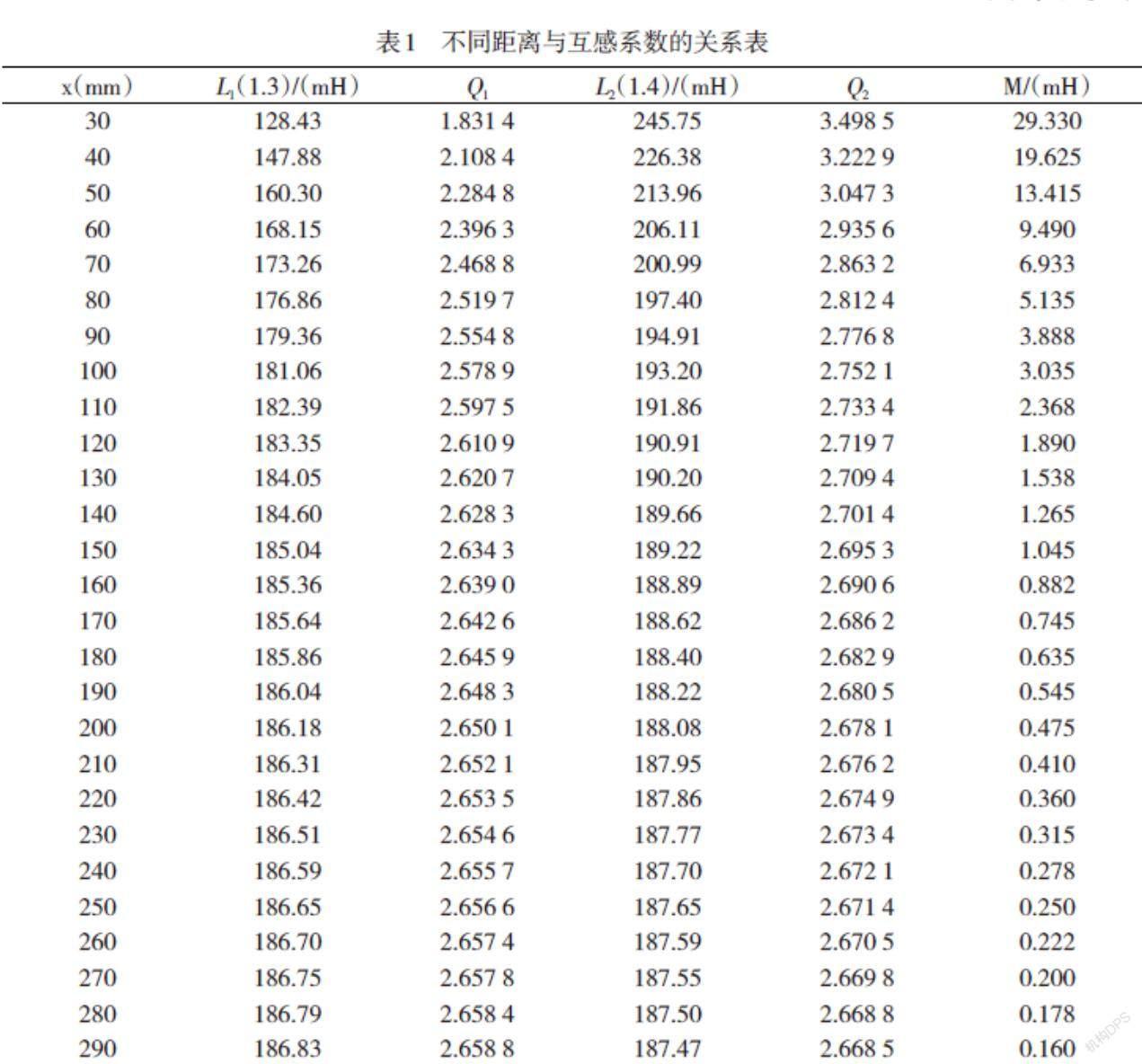
如圖1所示，將兩個繞組N1和N2的任意兩端（如1、3端）連在一起，用LCR測試儀測量電感值得到L1;再將兩個繞組N1的1端和N2的另一端4端連在一起，如圖2所示，用LCR測試儀測量電感值得到L2;如果L1>L2，則1、4為同名端，2、3為同名端;如果L2>L1，則1、3為同名端，2、4為同名端。

3 兩線圈互感系數M的測定

按照圖1和圖2連接線路，測量的相關數據如表1。從表1中可得出：L2>L1，則1、3為同名端，2、4為同名端，L1為反向串聯電感值，L2為順向串聯電感值，則互感系數表達式為：

M=（ L2- L1）/4? ?M=□（（L_2-L_1）/4）? ? ?（2）

根據式（2），計算的互感系數數據如表1。

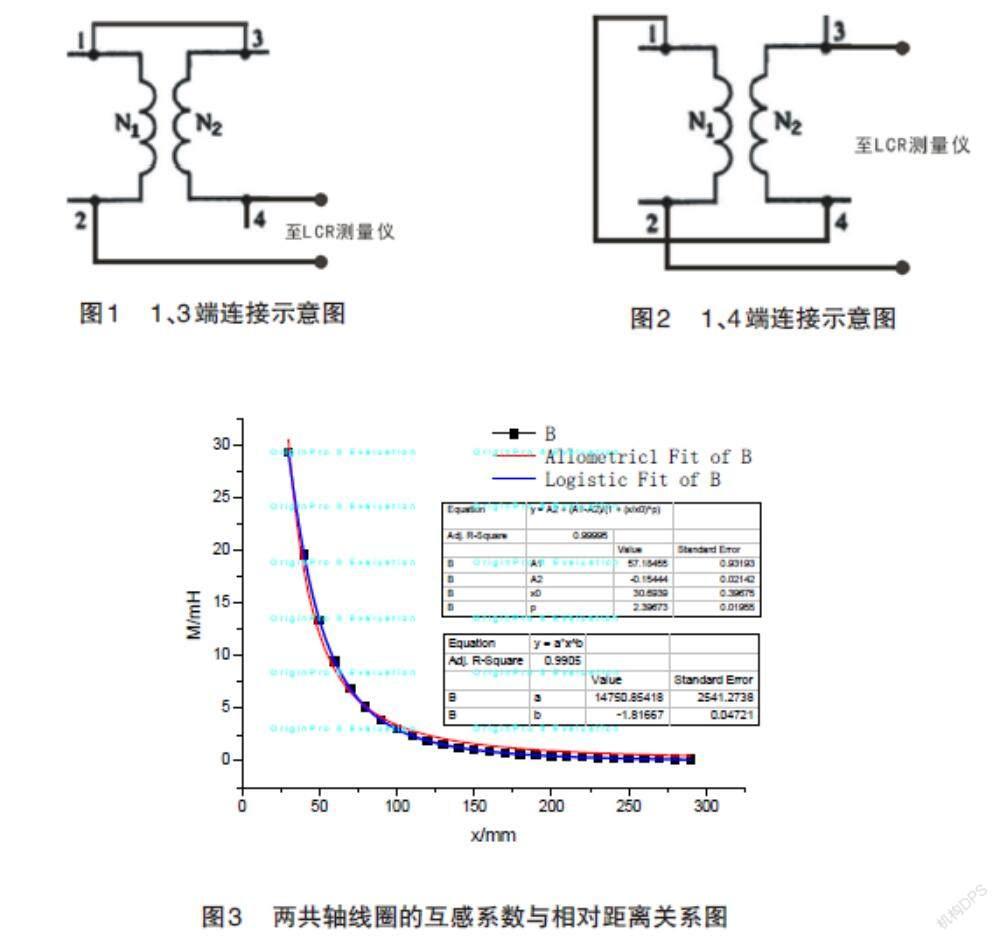
根據表1，利用Origin8.0做出圖形，如圖3。

利用Origin8.0對圖3擬合結果可以得出兩共軸線圈的互感系數與相對距離關系表達式為：

M=57.35/（1+（x/30.7 ）^2.4 ）-0.1544? ?（3）

擬合曲線相關系數為R2=0.99995，完全重合，非常完美。由Origin8.0擬合得到互感系數與相對距離關系式（3）與文獻[4]中由“數值計算和曲線擬合的方法”得到了共軸等大圓線圈間互感系數的結果近似。

3 結語

同軸線圈的相互作用能和相互作用力都與互感系數密切相關，對于其值的計算或者測量就會直接影響到相應的同軸線圈的工程應用，而互感系數的計算需要先利用畢奧-薩伐爾定律導出的互感系數積分公式，再進行數值計算，積分計算過程繁瑣，計算量大。因此通常用實驗的方法測定，常用實驗方法有：暫態法、磁通法、伏安法、串聯法等，這些方法在測量互感系數時，有些測量要求比較高、有些計算量比較大，都不夠理想。該文利用LCR數字電橋測量出同名端的順向串聯和反向串聯值可以計算出互感系數，這種方法相對來說測量操作簡單，且隨著現代科技的發展，實驗儀器測量精度不斷提高，實驗方法不斷優化，實驗測量得到的結果也越來越接近理論值。Origin8.0強大的數據處理功能也被運用到兩共軸線圈的互感系數與相對距離函數關系式的建立中，且得到的結果與計算得到的變化規律一致。實驗測量互感系數的方法與電腦程序運用將會被更廣泛的運用。

參考文獻

[1] 張偉，陳俊斌.同軸等大線圈互感系數及相互作用力的近似解析公式[J].大學物理，2004（8）：36-37，40.

[2] 龔禔.一般情況下兩共軸圓線圈間互感系數的簡便計算[J].大學物理，2011，30（4）：46-48.

[3] 熊慧，劉來，劉近貞.任意空間位置下改進的互感系數計算方法[J].傳感器世界，2018，24（6）：7-11.

[4] 張若舟，秦明陽，張露，等.超導薄膜磁場穿透深度的雙線圈互感測量[J].物理學報，2020，69（4）：249-258.

[5] 王鵬.通電直螺線管自感與互感的物理圖像[J].物理通報，2021（7）：39-42.

[6] 周群益，莫云飛，侯兆陽，等.兩共軸環電流之間的互感系數和作用力[J].大學物理，2020，39（10）：5-11.

[7] 范宜標，陳晶晶，林炳輝.基于自由軸法便攜式LCR測試儀的設計與實現[J].黑河學院學報，2018，9（11）：210-212.

[8] 王環江，吳怡逸，肖寒，等.Origin8.0用于物理化學實驗數據擬合處理[J].山東化工，2020，49（9）：218-221，228.

[9] 岑敏銳.同軸等大方形線圈的互感系數[J].武漢工程大學學報，2007（4）：90-92.