動車組受電弓可靠性數據分析

薛 康，齊金平,2,3，徐安策，周亞輝，李少雄

（1. 蘭州交通大學 機電技術研究所，蘭州 730070；2. 甘肅省物流及運輸裝備信息化工程技術研究中心，蘭州 730070；3. 甘肅省物流與運輸裝備行業技術中心，蘭州 730070；4. 中國鐵路蘭州局集團有限公司 辦公室，蘭州 730015）

隨著我國高速鐵路（簡稱：高鐵）技術的快速發展，動車組成為我國高鐵客運的主要運營列車。動車組的運行安全直接關系到高鐵客運的安全，以及社會和經濟效益，這使動車組列車安全運行數據的可靠性分析變得極為重要。

1 研究背景

可靠性指產品在規定的條件下和規定時間內，完成規定功能的能力[1]。可靠性數據是可靠性研究的基礎。可靠性參數估計通過可靠性模型，對數據的可靠性指標進行定量分析和評估的過程。

文獻[2]對動車組牽引系統進行了故障統計分析，并指出受電弓是高壓電器的薄弱環節，其故障數量占高壓電器故障總數的67.64%。文獻[3]分析了動車組牽引傳動系統的故障數據，得到牽引傳動系統主要零部件的可靠性特征函數，找出了故障變化的規律。文獻[4-5]以CRH3型動車組牽引供電系統的故障數據為樣本進行分析，得到了可靠性指標。文獻[6]根據動車組的實際故障數據，對牽引傳動系統進行可靠性分析，獲得系統組成部件靜態和動態的可靠性參數。文獻[7]研究了設備可靠性建模方法，并用該方法對設備故障數據進行分析，得到了設備可靠性指標函數。

受電弓是動車組高壓牽引系統的關鍵組成部分[8]，是動車組從接觸網獲得電能的主要設備，能夠為動車組運行提供牽引動力。本文以某高鐵線的CRH3型動車組受電弓在不同運營時間段的故障數據為例，分析故障數據的分布，得出不同運營階段受電弓的可靠性指標，為動車組的安全運行提供指導。

2 研究方法

2.1 可靠性數據分析

在產品的可靠性分析中，可靠性常常是一個概率值，因此，可靠性數據分析是進行數據可靠性定量評估的前提。隨著可靠性工程研究理論的發展，可靠性數據分析的重要性逐漸凸顯。產品的可靠性、故障數據分布函數、失效率、可靠度等可靠性指標都通過可靠性數據分析獲得。

可靠性數據分析的流程如圖1所示。

圖1 可靠性數據分析的流程

2.2 數據分布類型

對產品進行可靠性數據分析，需要了解失效數據的分布類型，根據分布類型得到可靠性指標。常見的數據分布有正態分布、指數分布、威布爾分布等[9]，其中，威布爾分布對各種失效數據的處理能力很強，可以描述早期失效、偶然失效和耗損失效這3種類型[1]。

威布爾分布函數如式（1）所示。

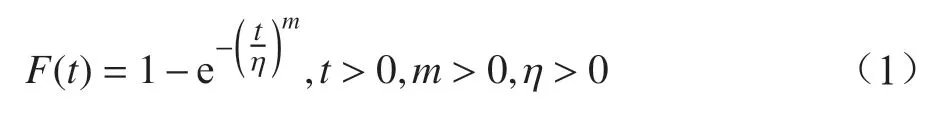
其中，t為故障時間；m為形狀參數；η 為尺度參數。

2.3 威布爾分布概率圖

概率圖是一種通俗簡便的評估方法，通過將數據進行轉換，擬合成一條線性回歸線來檢驗樣本總體的分布類型。概率圖能夠評估數據分布的擬合程度，并對該分布的某些特征值進行估計，具有直觀、簡便、快速等優點。

在處理故障數據時，比較常用的概率圖是威布爾分布概率圖。若故障數據在威布爾概率圖中分布在線性回歸線兩側，即可認為該數據服從威布爾分布。

2.4 最小二乘法

最小二乘法是將數據分布函數經過恰當的變換之后，求解參數的估計方法[10-11]。

對威爾布分布函數進行變形[12-13]處理，得到式（2）。

對式（2）等號兩側同時進行兩次對數運算，可得

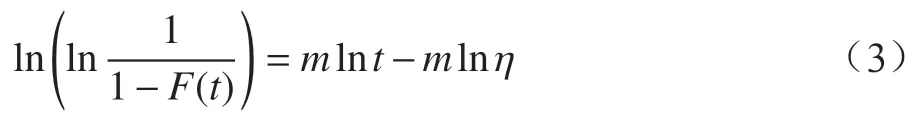
經過上述變換后，在t - y坐標下的圖形即為威布爾分布概率圖，能夠對數據分布進行擬合程度評估。實際參數估計中，y常被轉化為數據樣本的中位秩值。

中位秩是在n個樣本第i次失效時，真實失效概率在50%的置信水平上應有的值，或者是不可靠性的最佳估計值。中位秩計算如式（5）所示。

其中，i為數據樣本排序序號；n為數據樣本總數。

結合最小二乘法原理，由式（4）可得，參數m和b0的估計值為

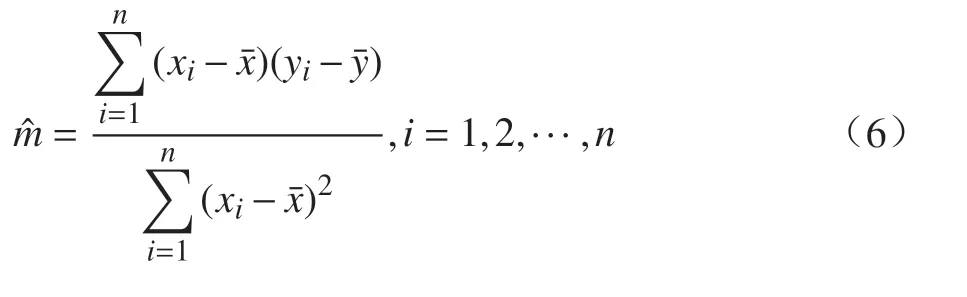
由此得出威爾布分布函數的參數 η估計值為

2.5 K-S檢驗

K-S（Kolmogorov-Smirnov）檢驗[14-15]是比較一種頻率分布與理論分布或者兩個觀測值分布的檢驗方法。通過對觀察數據的累積概率分布函數g(t)與擬合計算所得分布的累積概率分布函數f(t)進行比較，得出二者的偏差值在置信度 α的臨界值內，即認為對故障數據的擬合分布符合理論分布。

3 故障數據分布

3.1 數據處理

本文以受電弓分別在2012—2013年和2018—2019年運行過程中產生的故障數據為樣本，進行可靠性數據分析。本文以故障間隔里程（即無故障運行公里數）為依據，對受電弓在運營過程中的故障數據（即故障間隔里程）按從小到大的順序進行排列，并計算它們的中位秩。兩組故障數據及其中位秩分別如表1和表2所示。

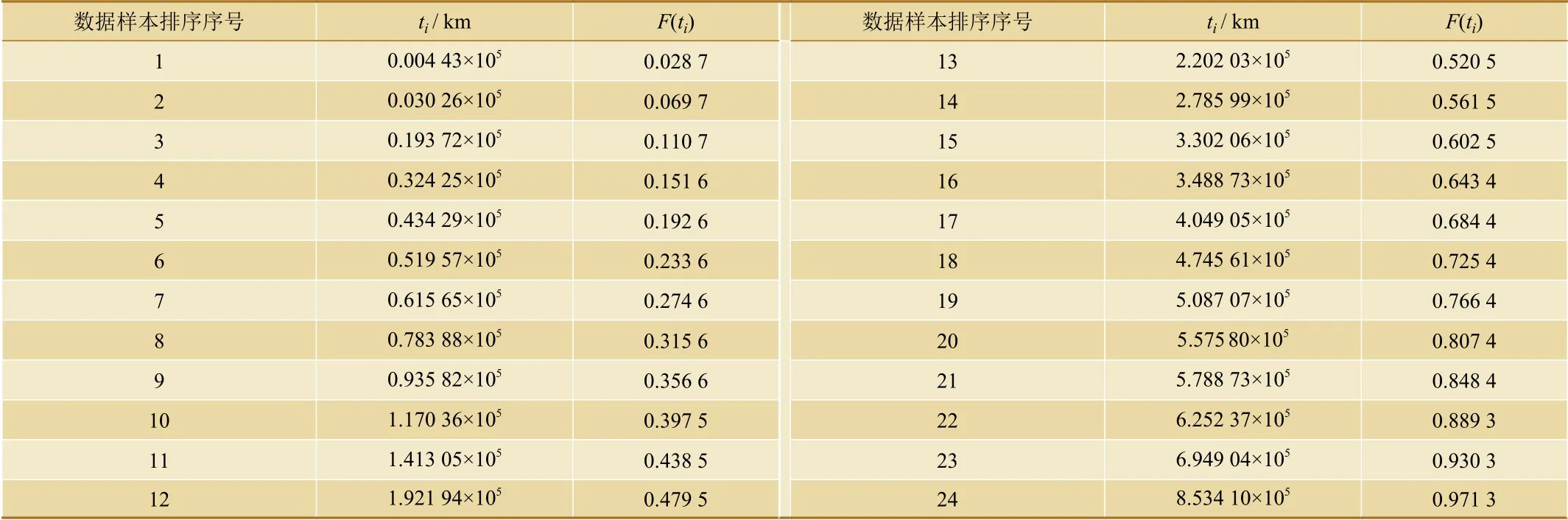
表1 某高鐵線受電弓故障數據及其中位秩（2012—2013年）

表2 某高鐵線受電弓故障數據及其中位秩（2018—2019年）

根據上述受電弓故障數據繪制兩組故障數據的威布爾分布概率圖，如圖2所示。可以看出，大部分數據點分布在直線兩側，因此，本文認為受電弓故障數據服從威布爾分布。

圖2 故障數據威布爾分布概率圖

3.2 數據分布參數估計

本文采用最小二乘法進行參數估計，對受電弓的兩組故障數據進行擬合，得到受電弓故障數據的威布爾分布參數。

令

其中，ti為故障數據；F(ti)為ti對應的中位秩。根據式（9）和式（10）來計算故障數據，得到的結果如表3和表4所示。

根據表3和表4的計算結果，以及式（6）和式（8），計算得出2012—2013年和2018—2019年這兩組故障數據威布爾分布的形狀參數m和 尺寸參數 η的估計值分別為

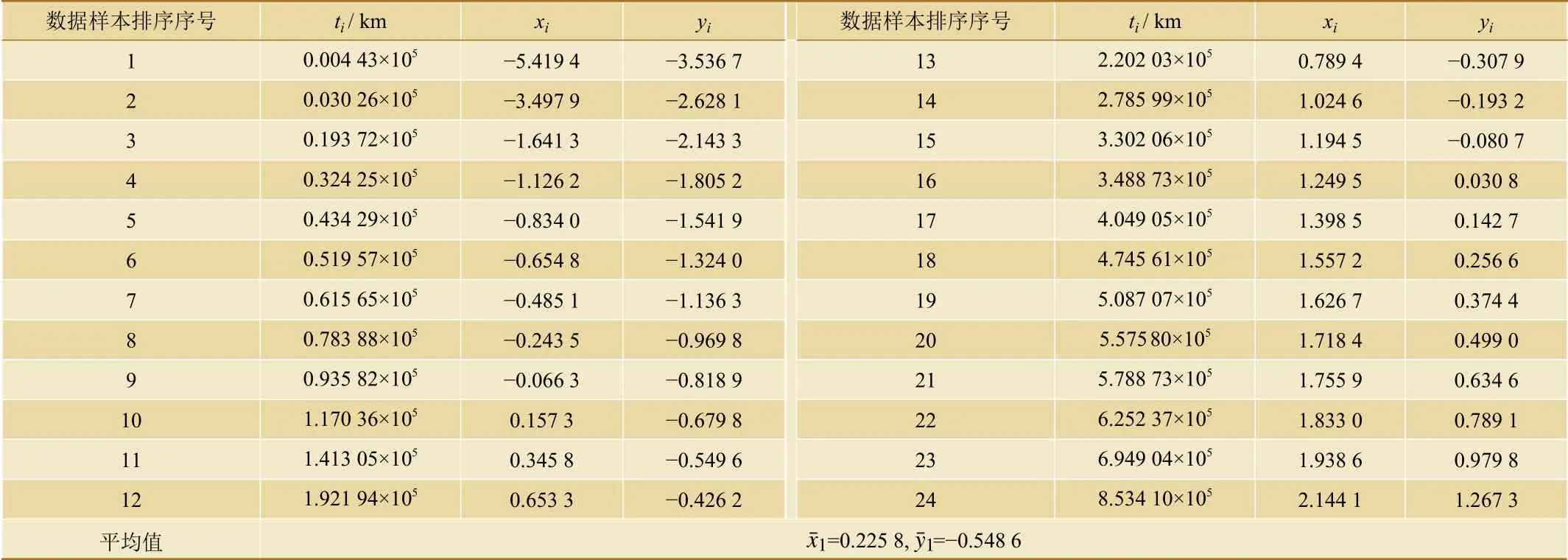
表3 某高鐵線受電弓故障數據計算結果（2012—2013年）

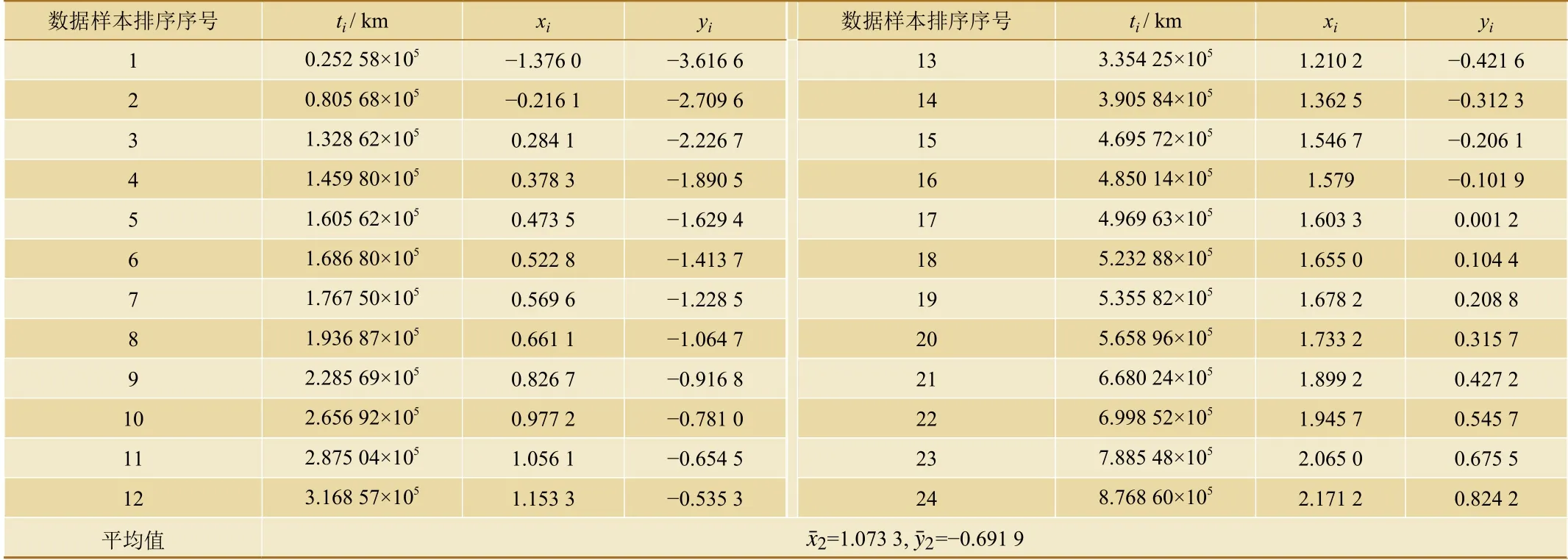
表4 某高鐵線受電弓故障數據計算結果（2018—2019年）

由此可知，兩組故障數據的威爾布分布函數分別為

4 結果分析

4.1 故障數據分布評估

由式（11）和式（12）可知，在不同運營時間段受電弓故障數據服從不同參數的威布爾分布。本文對故障數據進行K-S檢驗，將故障數據的累積概率密度與擬合的威布爾分布累積概率進行對比，如圖3所示。

由圖3可以看出，不同時期的受電弓故障數據的累積概率密度曲線與所擬合的威布爾分布累積概率曲線趨勢接近，因此，本文認為受電弓的故障規律符合威布爾分布。

圖3 累計概率密度曲線對比

4.2 可靠性指標計算

威布爾分布可靠度函數和失效率函數分別為

將擬合結果代入式（13）和式（14），可得受

可靠度函數及失效率函數曲線如圖4 所示。電弓這兩組故障數據的可靠度函數分別為

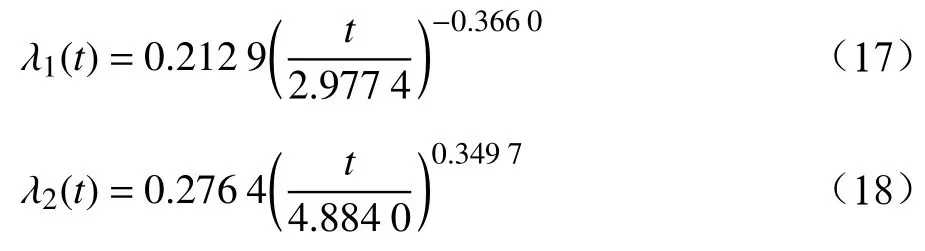
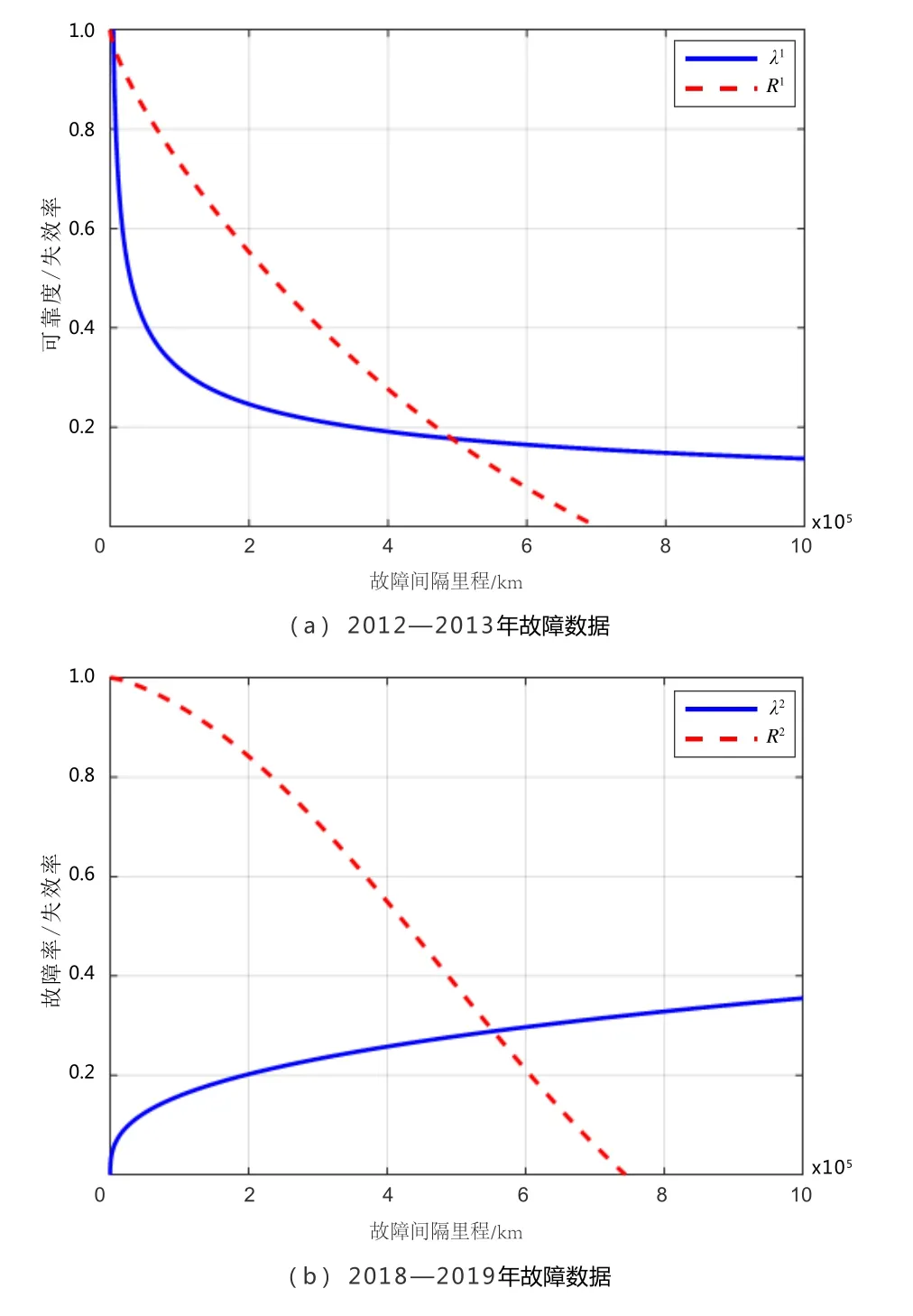
圖4 可靠度函數和失效率函數曲線

失效率函數分別為

根據威布爾分布的性質，并結合失效率函數圖像可知，根據參數估計結果，當m1=0.6340，即m＜1時，動車組受電弓處于早期失效類型，其故障率隨運營里程增加呈現下降趨勢；當m2=1.3497，即m＞1時，動車組受電弓處于耗損失效類型，受其故障率隨運營里程增加呈現上升趨勢。

5 結束語

本文研究了CRH3型動車組受電弓在不同運營階段的故障數據，對其分布進行了估計，得到了故障數據符合威爾布分布的結論，并計算了威爾布分布可靠性指標。實驗證明：受電弓在早期運營階段故障率高故障頻發，后期運營階段故障率逐漸降低。未來，本文將對不同階段數據的多源融合進行分析，進一步提升故障分布模型的精度，為不同時間上線運營的動車組檢修與故障預測，提供理論依據。