自動接發球機發球過程損耗時間與誤差補償研究

王 晗，楊麗紅

(上海理工大學 機械工程學院，上海 200093)

“青少年籃球運動技能等級標準與測試”是一種國家對青少年籃球技能評價標準及方法[1-3]，測試流程為被測試者先將球傳給自動接發球機，迅速跑到接球點接回傳球。自動接發球機發出的籃球，能否在指定的時間到達指定的接球點，影響著考核的成績。

研究者[4-7]對國內外摩擦輪式發球機的發球原理進行研究。杜小雷[8]對摩擦輪式發球機發球后籃球在飛行過程進行受力分析，建立其飛行過程中的運動模型。鐘建琳等[9]設計了一款集收發球功能為一體的投球機器人。摩擦輪式發球機構通過籃球與發球機構之間的擠壓接觸，產生的粘彈性摩擦力傳動發球，傳動過程需要一定時間[10]，而以上研究并沒有考慮發球機構發球過程損耗時間而造成的發球誤差。

在建立適用于“青少年籃球運動技能等級標準與測試”的發球模型后，為減少機械因素對考核結果的影響，需對自動接發球機發球過程損耗時間做研究。課題組通過采集摩擦輪發球機構發球過程中的伺服電機轉矩變化的時間長度，得到不同目標出球速度、摩擦輪間距與發球機構發球過程損耗時間的關系，以此建立誤差補償模型。

1 接發球機工作原理

1.1 分級考核中接發球機工作流程

以“標準”7級測試中的Ⅰ號接發球機為例，被測人從出發區出發，將球傳至Ⅰ號發球機，跑動到接球點1，接住自動接發球機發出的回傳球，后續過程類似，完成考核的總時間決定成績。分級考核發球機工作示意圖如圖1所示。

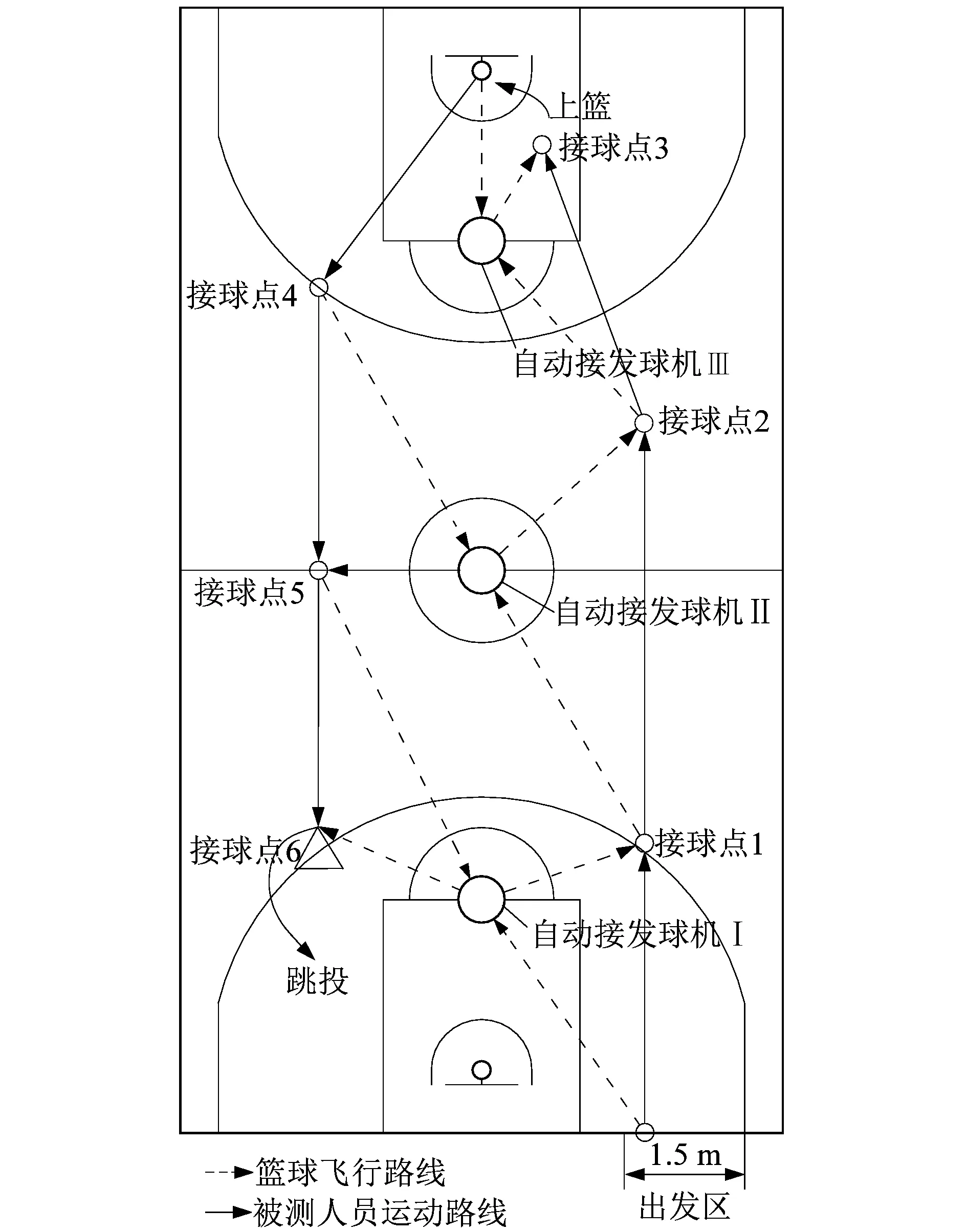
圖1 分級考核接發球機工作示意圖Figure 1 Working diagram of receiving and serving machine in grading assessment

1.2 發球機構和發球模型

自動接發球機采用摩擦輪式發球，如圖2所示。電機帶動2個旋轉方向相反的摩擦輪，籃球進入摩擦輪中間，獲得一定的出球速度，出球速度與摩擦輪線速度不相等[11]。在接球點確定的情況下，接球距離L、接球高度h和發球高度h0確定。自動接發球機根據被測者運動速度確定其到達接球點時間ta，選定籃球飛行時間t。籃球飛行時間t、接球距離L、接球高度h、發球高度h0，與籃球出球角度θ、速度V成一定關系[8]59：

(1)

(2)

籃球出球速度V與發球機構的摩擦輪線速度Va關系[12]：

Va=-0.058 81V3+1.258V2-6.21V+16.76。

(3)

具體發球邏輯為：將某一接球情況下的L，h，h0，t代入公式(1)和(2)，求得籃球出球速度V、出球角度θ，將籃球出球速度V代入公式(3)得到接發球機摩擦輪線速度Va，PLC控制接發球機以求得θ，Va，在時間(ta-t)后發球。

2 發球機構損耗時間實驗

由于籃球與摩擦輪表面都為粘彈性材料，粘彈性摩擦與接觸面積、接觸速度等因素相關[13]，且具有滯后性、高非線性的特點[14-17]，難以通過理論計算得出籃球在摩擦輪中獲取速度所耗時間。因此通過實驗測量方法，直接獲得摩擦輪間距、轉速與發球過程所耗時間關系，從而實現發球過程損耗時間的誤差補償模型的建立。

2.1 實驗器材與方法

發球過程時間短、速度快，難以精確測量發球過程所耗時間。因此課題組提出一種發球損耗時間采集方法：通過伺服電機驅動器，采用RS232通信協議與上位機通信，采集發球機構發球過程籃球從接觸摩擦輪到離開摩擦輪過程電機由于負載變化導致的轉矩變化的過程的時間長度，從而獲得在自動接發球機在發球過程中損耗時間。數據采樣間隔為1.25 ms，采樣點數為250。查閱相關文獻[7]15，確定實驗中電機轉速為1 400～3 000 r/min，摩擦輪的中心距取335和345 mm。

采用型材搭建實驗設備如圖3所示，摩擦輪由伺服電機驅動，摩擦輪中心距可調。摩擦輪材料為聚氨酯彈性體，硬度為50邵A，直徑為128 mm，寬50 mm。籃球為7號球，表面材料為PU，氣壓為標準48.265 kPa。伺服電機為低壓直流伺服電機，功率400 W，額定電壓48 V，額定扭矩1.28 N·m。通過PLC控制伺服電機轉速。

圖3 試驗設備Figure 3 Test equipment

2.2 實驗結果

在不同轉速和摩擦輪間距情況下，采集籃球發球過程中電機轉矩隨時間的變化曲線如圖4所示。

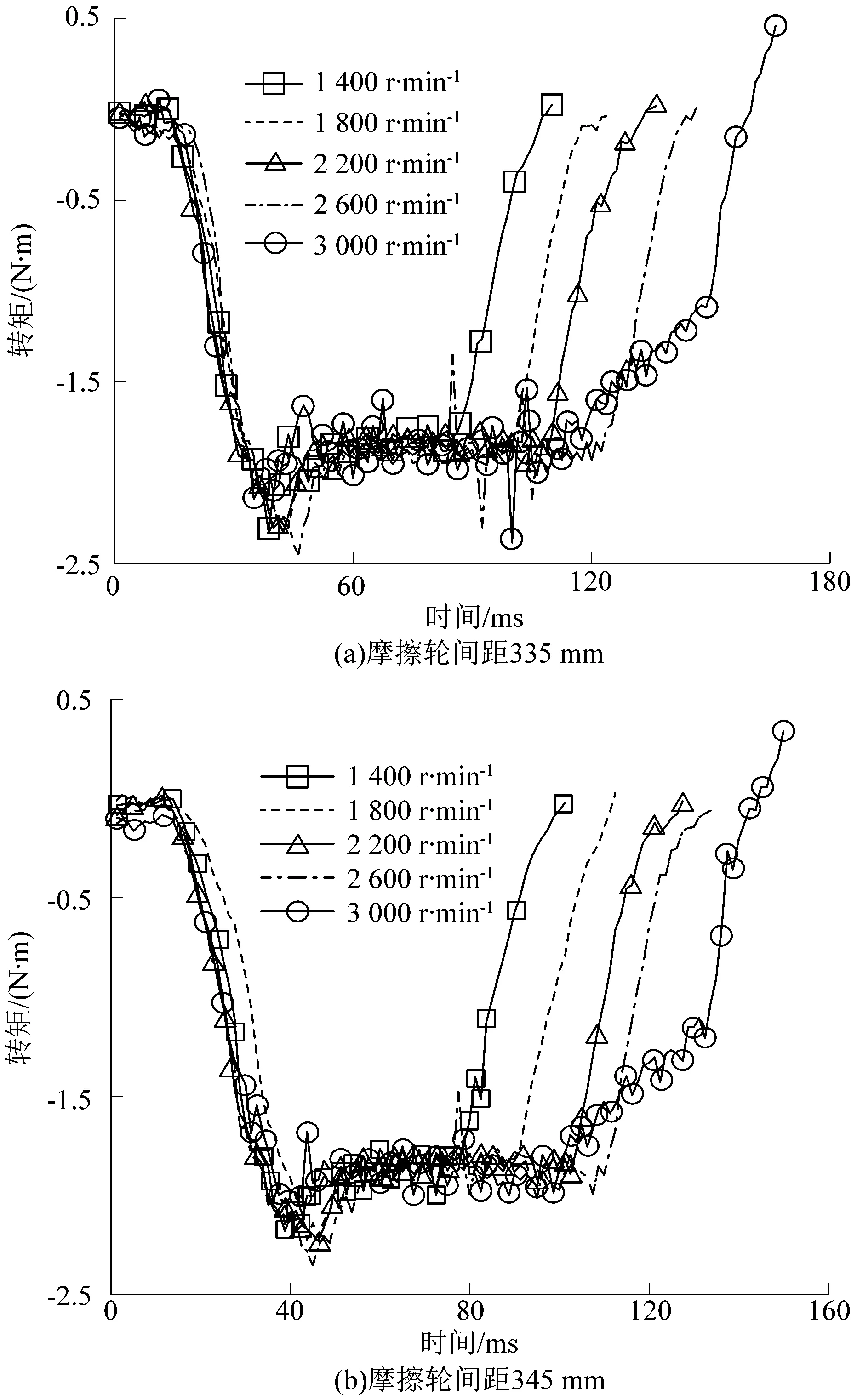
圖4 電機轉矩隨時間變化情況Figure 4 Curves of torque change with time

以電機轉矩突變過程的時間為籃球在發球機構中為獲得指定速度而損耗時間，對實驗結果數據進行處理，結果如圖5所示。

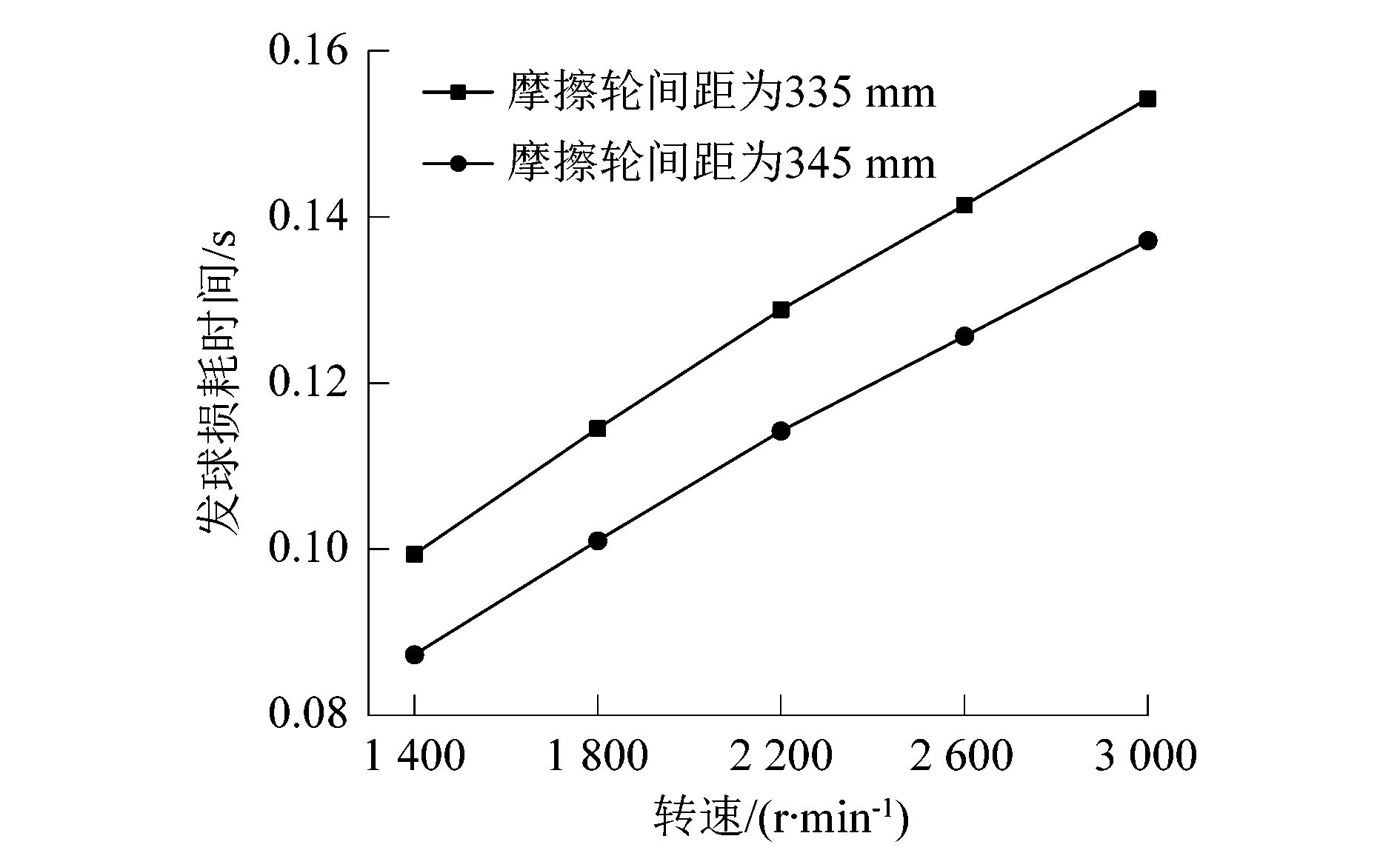
圖5 發球機構損耗時間與轉速的關系Figure 5 Relationship between loss time and rotation speed of service mechanism

從圖5中可以得出，發球機構發球損耗時間和電機轉速呈線性關系，發球損耗時間隨著轉速增大而增大，隨著摩擦輪間距減小而增大。對發球過程損耗時間的誤差補償應根據不同發球初始參數來確定。

2.3 發球損耗時間的誤差補償模型

以摩擦輪間距為335 mm時，轉速對應的發球過程損耗時間建立誤差補償模型。以摩擦輪線速度Va為自變量，發球過程損耗時間tb為因變量，通過MATLAB對實驗數據進行曲線擬合，得出：

tb=0.005 091Va+0.052 62。

(4)

3 討論

由公式(1)～(2)可知，籃球以一定的出球速度V、出球角度θ，在空中飛行時間t后，到達指定接球點。若不考慮發球機構發球損耗時間tb，則籃球實際在空中飛行的時間為t-tb，導致考核人員到達接球點時而籃球還未到達指定位置。理論計算驗證了對發球過程損耗時間tb進行誤差補償的必要性。設在考核過程中，給定3個接球情況的接球距離L、接球高度h,、發球高度h0和籃球選定飛行時間t，具體參數如表1所示。

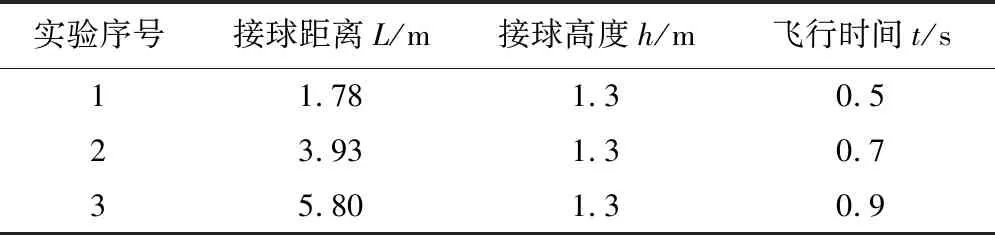
表1 試驗參數取值Table 1 Validation of experimental factors

將表1參數代入公式(1)和(2)，得到籃球對應出球速度V和出球角度θ。將V代入公式(3)，得到發球機構的摩擦輪線速度Va，將Va代入公式(4)求得tb。計算籃球以出球速度V、出球角度θ，實際飛行時間t-tb后的實際位置與考核要求接球點的接球高度和接球距離的誤差，無時間補償模型理論計算結果如表2所示。

表2 無時間補償模型理論計算結果Table 2 Theoretical calculation results of no time compensation model

由表2可知，未考慮發球機構發球損耗時間tb的發球模型，發球距離誤差最大為21.9%，發球高度誤差最大為30.80%，籃球在發球機構中的時間損耗對發球精度有巨大影響，不可忽略。

通過公式(4)對發球過程的時間損耗進行補償。具體補償邏輯如下：自動接發球機根據被測者運動速度確定其在時間ta后到達接球點，選定籃球飛行時間t，通過公式(1)和(2)得出籃球接發球機的發球角度θ、出球速度V，將出球速度V代入(3)式求得摩擦輪線速度Va，將Va代入公式(4)得到補償時間tb，自動接發球機通過PLC控制發球作業在時間ta-(t+tb)后開始。

4 結語

自動接發球機的發球機構發球過程損耗的時間會導致發球誤差，課題組通過研究自動接發球機的發球機構發球損耗時間與摩擦輪間距、轉速的關系，以此建立了摩擦輪間距為335 mm時的摩擦輪線速度與發球過程損耗時間的誤差補償模型。實驗結果表明：發球機構發球損耗時間與摩擦輪轉速成正比，與間距成反比；考慮發球損耗時間誤差補償的發球模型，發球精度提升最大30.80%，對于“青少年籃球運動技能等級標準與測試”考核過程中，起到減少發球誤差，提高考核過程的可靠性的作用。