基于正弦反饋Logistic混沌映射的圖像加密算法及其FPGA實現

李春彪 趙云楠 李雅寧 孔思曉

(南京信息工程大學電子與信息工程學院 南京 210044)

1 引言

數字圖像的安全傳輸和隱私保護在網絡空間中易受挑戰，而傳統分組加密算法容易遭受窮舉法的攻擊。由于圖像數據具有特殊格式，圖像加密對加密效率有更高的要求。分組加密算法對圖像的加密具有一定的局限性，故而常用于文字符號等信息的加密。大量的圖像加密方案也將明文圖像視為文本數據來處理[1]，這使得傳統分組加密算法的效率不夠高。目前，先進的拍攝設備使數字圖像具有大數據量和高冗余的特點，加之數字圖像本身的相鄰像素相關性高[2]，分組加密算法難以削弱相鄰像素相關性。

隨著混沌理論的發展，人們將混沌理論引入密碼學形成新的數字圖像加密算法[3]。混沌具有遍歷性、隨機性和初值敏感性等特點，其混合和隨機性類似于密碼學的置換和擴散。混沌加密算法使得加密安全性更高、密鑰空間更大、密鑰敏感性更強，比傳統加密方法更有潛力[4]。然而數字圖像的混沌加密算法也面臨著安全性能方面的挑戰。基于混沌系統的偽隨機序列發生器存在一定的弱隨機性[1]。

典型的Logistic映射的數學表達式簡單但動力學特性復雜。文獻[5]從離散序列和相對熵的理論中分析了Logistic映射的時間不可逆性、初值敏感性、混沌狀態程度等特性，因而可以采用Logistic映射或者改進Logistic映射來加密數字圖像。文獻[6]采用了典型的Logistic映射進行數字圖像加密，該方法能夠實現良好的加密效果，但密文圖像的灰度直方圖不平坦，加密效果欠佳；文獻[7]改進Logistic映射并基于初始值與控制參數之間存在的關系對變量域進行分段處理，擴大了混沌域；陶紅[8]試著將典型的Logistic映射與其他加密方式相結合來改善加密效果。上述加密方式均基于單一混沌映射進行數字圖像加密。

本文在經典Logistic映射中引入正弦反饋，構成新的映射關系，并對生成的偽隨機序列進行預處理，增強其偽隨機性，削弱偽隨機序列發生器的弱隨機性造成的弊端。使用NIST隨機數測試法測得加密序列的偽隨機性較好。FPGA系統穩定性高，可用電路直觀表達邏輯，且成本較低[9]。利用FPGA進行加密處理，數據穩定性更強，邏輯更清晰。本文使用FPGA平臺，實現本文提出加密方案，加密效果較好。

2 引入正弦反饋的Logistic映射

2.1 映射數學模型

基于Logistic映射[10]，引入正弦函數，構建出新的1維混沌映射，其函數如式(1)所示

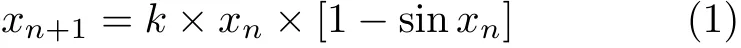
其中，k為系統數且k ?=0。

2.2 一次映射不動點穩定性分析

已知新的混沌映射函數式(1)，存在不動點xf,xf滿足方程

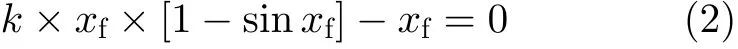
解得

2.3 分岔圖與Lyapunov指數分析

在初值為x0=0.1的情況下，計算狀態量x(n)的分岔圖和Lyapunov指數譜，如圖2所示。從圖中可以看出引入非線性正弦因子的Logistic混沌系統的混沌區域大，使用該混沌系統能得到更寬的加密區間。Lyapunov指數表征了一個系統的混沌屬性[13]。比較分岔圖與Lyapunov指數譜，可以看出分岔圖在最大Lyapunov指數為零時便會進入新的分岔。可以看出引入正弦因子的Logistic混沌系統的Lyapunov指數大于零的范圍很寬，總的密鑰空間也較大。當k=3.584時，混沌分岔圖開始分岔，從周期1進入周期2；當k=4.428時，從周期2進入周期4，當k=4.627時，從周期4進入周期8，并繼而進入混沌態。

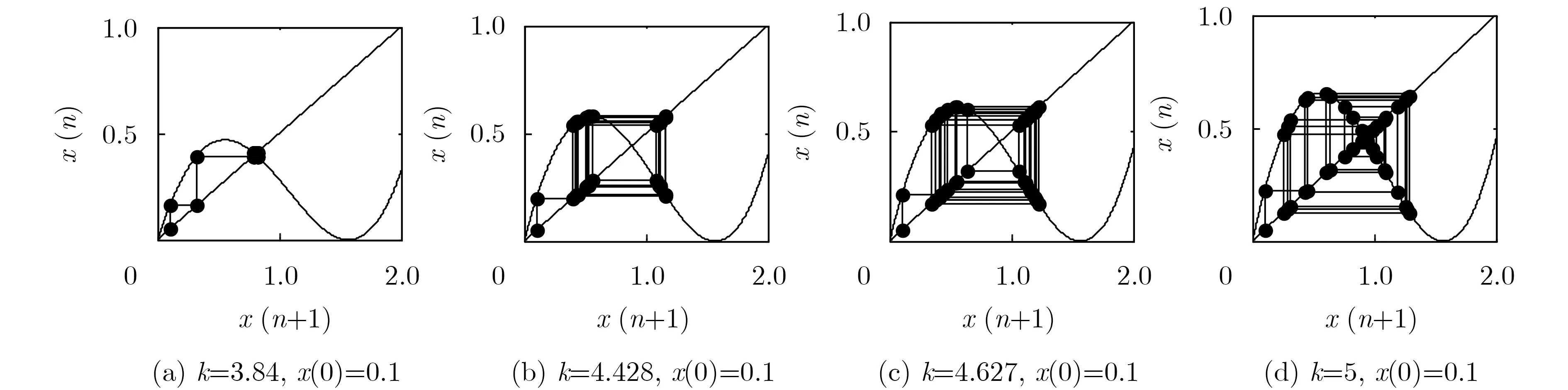
圖1 蛛網結構圖

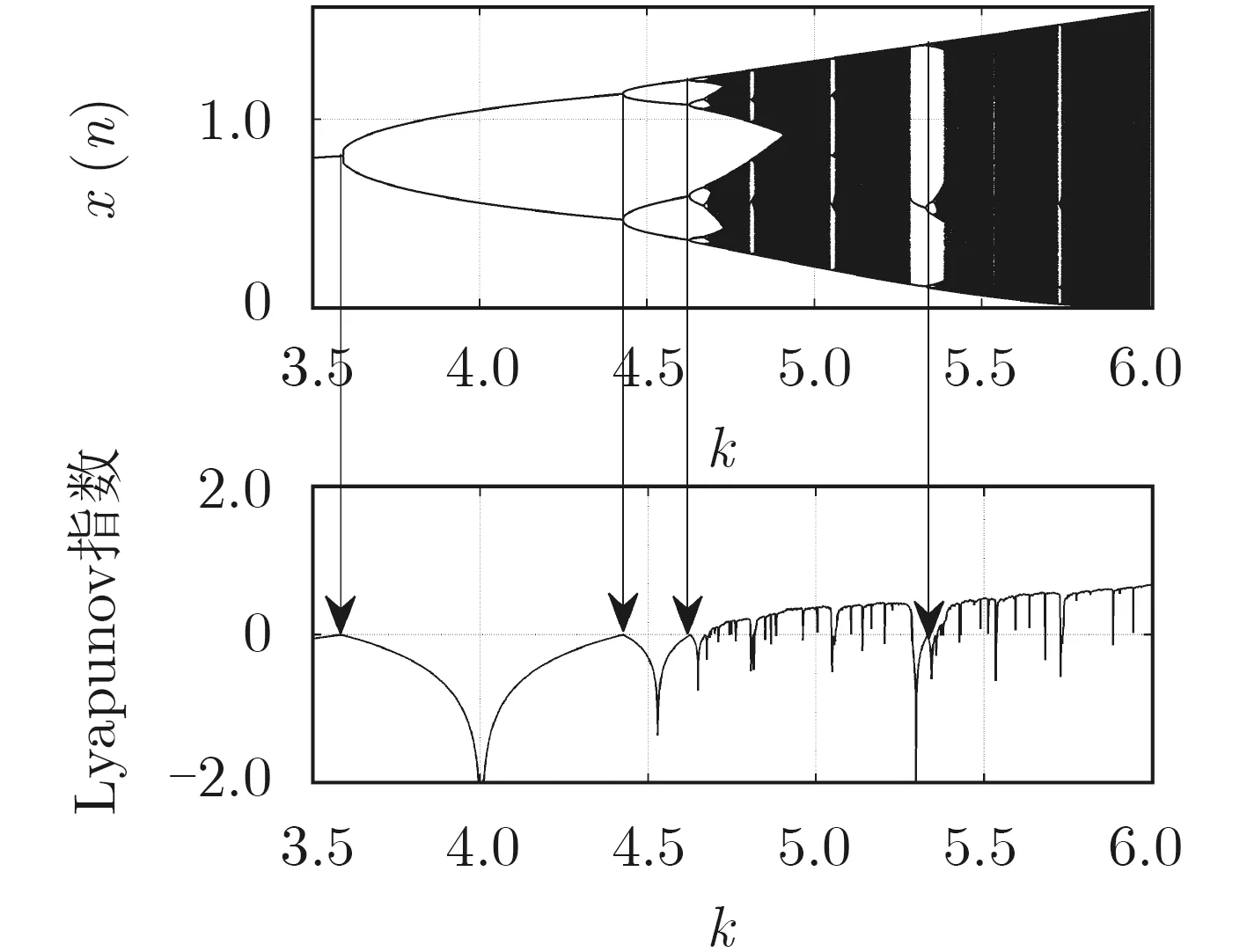
圖2 分岔圖和Lyapunov指數譜圖

2.4 敏感性分析

密鑰敏感性表征了密碼系統的安全性能[14]。敏感性高表明了密鑰微小的擾動便無法解密密文圖像。引入非線性正弦因子的Logistic混沌系統的敏感性如圖3所示。根據新混沌系統的系統方程，設初值x0=0.1，系統參數k=4.9，改變初值為0.1+10?4,0.1+10?8,0.1+10?12，迭代計算100次；設初值x0=0.1，系統參數k=4.9，改變系統參數為4.9+10?4,4.9+10?8,4.9+10?12，迭代計算100次。仿真得出的波形如圖3所示。從圖3中可以看出，密鑰一旦發生微小變化，迭代次數n增加后，密鑰序列變得完全不同，在圖中表現為兩條曲線的重合度。可見，密鑰敏感級別可達到10?12甚至更高的級別。

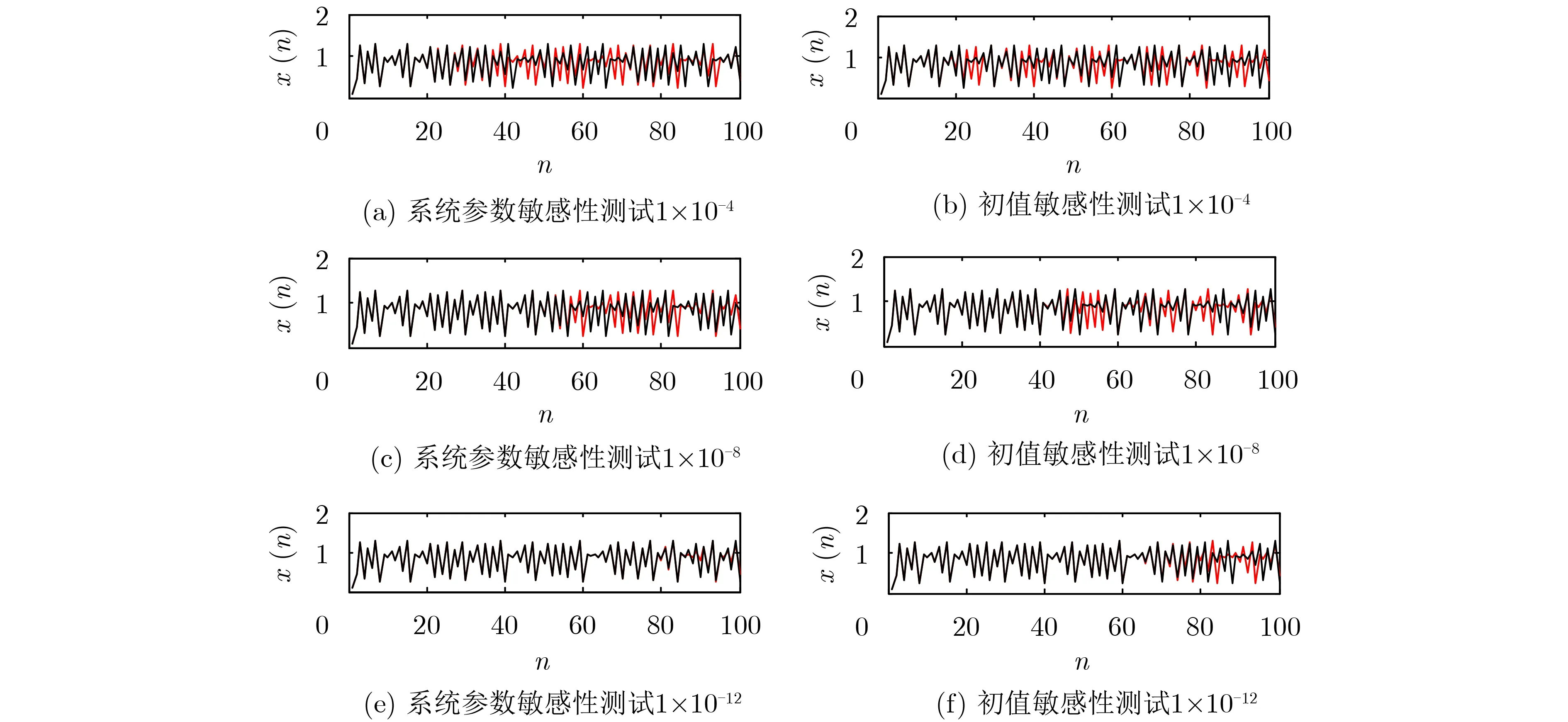
圖3 敏感性測試

3 加密性能測試

引入非線性正弦因子的Logistic混沌系統產生一個范圍在[0,1.6]的加密序列。該序列中可能存在大量相似數據。所以先對該加密序列進行預處理，增強該加密序列的偽隨機性，增強過程如式(6)所示。

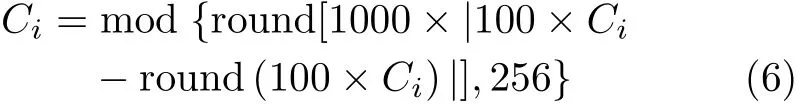
其中，mod()和 round()分別為取余和取整運算。該運算先將加密序列擴大取整，再取余計算，得到一組在[0,255]內的加密序列[15]。該預處理將加密序列放大取整，避免小數過多影響加密效果，并增強偽隨機性。加密/解密流程如圖4所示。密文圖像呈現噪聲樣式，無法解讀有效信息。解密圖像可以恢復明文信息。

圖4 引入正弦因子的Logistic加密解密過程

3.1 偽隨機性能測試

NIST發布的“隨機數和偽隨機數發生器統計測試組件”能全面地分析偽隨機序列的性能，具有頻率測試等15個測試的維度[16]，測試樣本為二進制。NIST對每個測試項都會生成P_value，當P_value>0.01時，則該測試通過；當P_value≤0.01時，則該測試不通過[17]。本文采用NIST推出的STS 2.1.2 (Statistical Test Suite 2.1.2)版本進行測試。

控制引入非線性正弦因子的Logistic混沌系統生成一組有262144個十進制數的偽隨機加密序列，為保證混沌效果，取后131072個數據并轉化成二進制文本。在STS界面設置100個大小為10000的數據塊，進行標準1-13的測試。再控制該混沌系統生成一組含有37500000個十進制整數的偽隨機加密序列，取后18750000個十進制數，二進轉化后進行標準14-15的測試。NIST測試結果如表1所示。被測偽隨機加密序列通過了15項NIST測試，且通過率均在97%以上，這表明該偽隨機加密序列具有較好的偽隨機性能。

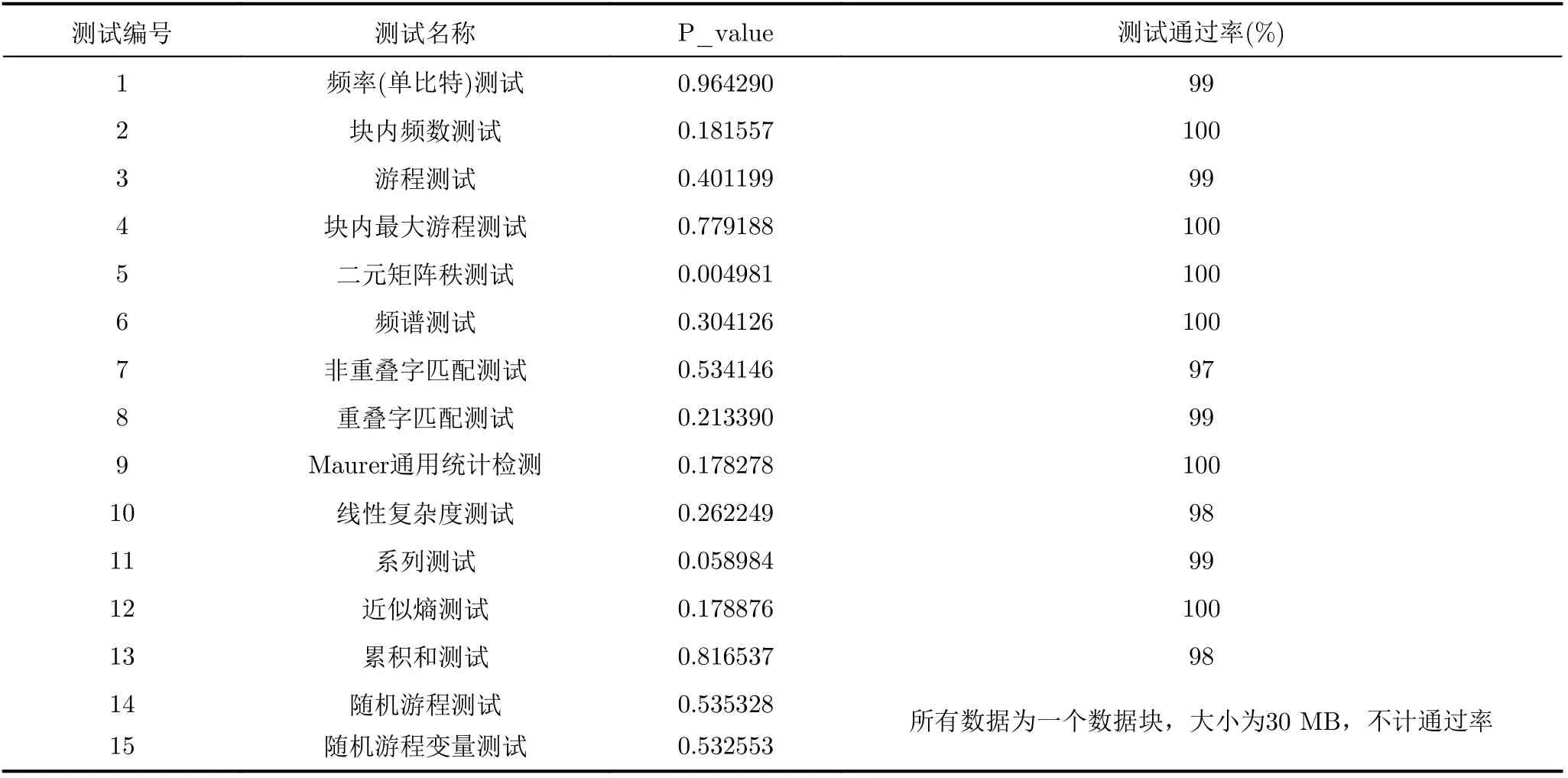
表1 NIST標準偽隨機測試結果

3.2 密鑰空間大小

本文所提出的引入非線性正弦因子的Logistic混沌加密系統的密鑰為K={x0,k}。在敏感性初值測試中，系統敏感性可達到10?17，密鑰的步進大小為10?18，每個密鑰由兩個參數構成，計算可得該密鑰空間大小為1034≈2114。由于2120>2100，可以判斷，該密鑰空間對窮舉法攻擊具有足夠的防御性[18]。

3.3 信息熵測試

熱力學采用熵值來表征物質狀態的無序性。類比熱力學，信息源信息的不確定度可由信息熵表示。信息源的熵值越大、紊亂程度越高，可接受信息越少。理論上，256灰度級完全隨機圖像的信息熵H為8。信息熵的計算公式如式(7)所示。式中K表示突出的灰度級個數，f(i)表示灰度i在所有灰度中出現的概率[19]。

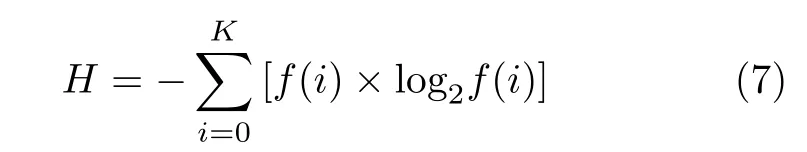
本文采用密鑰K={0.1,5}，以一副256灰度級的Lena圖像為例，計算其明文和其密文的信息熵，其計算結果列于表2中。由表2可知，密文圖像的信息熵為7.9987。引入正弦因子且對偽隨機序列進行預處理之后再加密，密文圖像具有較高的信息熵，圖像加密性能更加優越。

表2 信息熵實驗結果

3.4 密文統計特性測試

選取密鑰K={0.1,5}，利用引入非線性正弦因子的Logistic混沌加密系統和典型的Logistic混沌加密系統對圖像進行加密，繪制出密文圖像的灰度直方圖，如圖5和圖6所示。和典型Logistic混沌加密系統相比，引入非線性正弦因子的Logistic混沌加密系統得到的加密圖像的直方圖更加平滑，加密性能更優越。

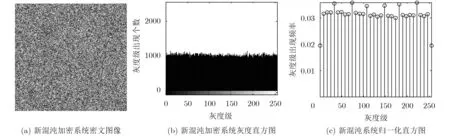
圖5 新混沌加密系統統計特性

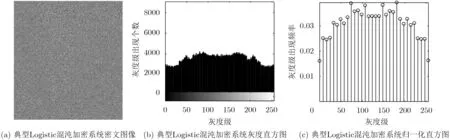
圖6 典型Logistic混沌加密系統統計特性

3.5 根據相鄰像素相關性分析

圖像的相鄰兩個像素主要分散于水平、垂直和對角線方向。加密后的圖像相關性小才能掩蓋原信息以防止信息泄露。計算公式如式(8)所示，從圖像矩陣中隨意抽選N對相鄰像素點的像素值，分別記為xi和yi[20]。

挑選8000對不同位置的相鄰像素點，計算相鄰像素相關系數并進行可視化處理。結果如圖7、圖8和表3所示。明文圖像的相鄰像素值呈現線性關系，相關性強；密文圖像的相鄰像素值均勻分布，相關性差。

表3 圖像的相鄰像素相關性

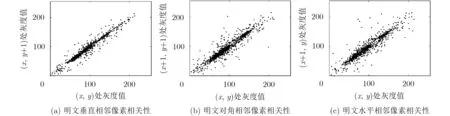
圖7 明文各方向相關系數

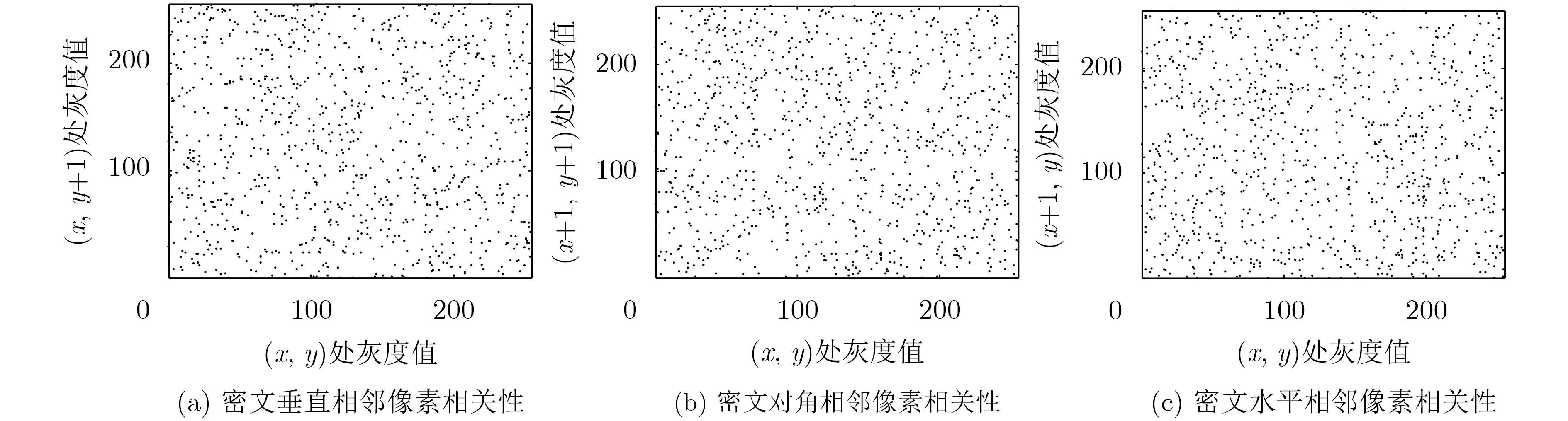
圖8 密文各方向相關系數

3.6 密鑰敏感性測試

上文的敏感性分析已表明引入非線性正弦因子的Logistic混沌加密系統具有密鑰敏感性。本節通過改變密鑰初值x0來測試密鑰敏感性。以密鑰K={0.1,0.4}進行加密。則密鑰x0=1.0+10?15無法解密，密鑰x0=1.0+10?17解密成功。這表明密鑰出現微弱擾動便無法解密圖像，十分敏感。如圖9與圖10所示。

圖9 密鑰為x0 =1.0+10?17時的解密過程

圖10 密鑰為x0 =1.0+10?15時的解密過程

4 FPGA加密和解密實現

4.1 硬件平臺介紹

本文采用的FPGA硬件實現平臺為Altera的以Cyclone IV EP4CE15F17C8N為核心的開發平臺。其開發環境為Quartus II 13.1。該FPGA配置了EPCS4芯片。其VGA接口驅動采用了專用的ADV7123轉換DA芯片。

4.2 加密/解密結構介紹

該加密/解密系統采用FPGA開發板的VGA顯示驅動、ROM存儲、JTGA下載功能。整個框架包含混沌加密序列發生模塊、圖像存儲控制模塊、程序下載模塊和VGA顯示模塊。通過JTGA接口將程序固化進FPGA的Flash。加密時，從ROM中讀取圖像數據和混沌加密序列，進行異或運算并通過VGA接口，將原圖、密文圖像和解密圖像依次顯示在顯示屏上。該混沌加密系統的結構框圖如圖11所示，解密系統結構框圖如圖12所示。

圖11 系統加密結構框圖

圖12 系統解密結構框圖

加密系統的RTL如圖13所示。其中clk為50 MB系統時鐘；rst_n為復位信號；vga_vs和vga_hs是VGA顯示器的行場掃描信號；vga_rgb(lcd_data)為輸出的加密圖像信號；image_data為原始圖像的信號；8位的信號pixel_data經過8到16位VGA信號轉換得到16位的vga_rgb信號輸出。

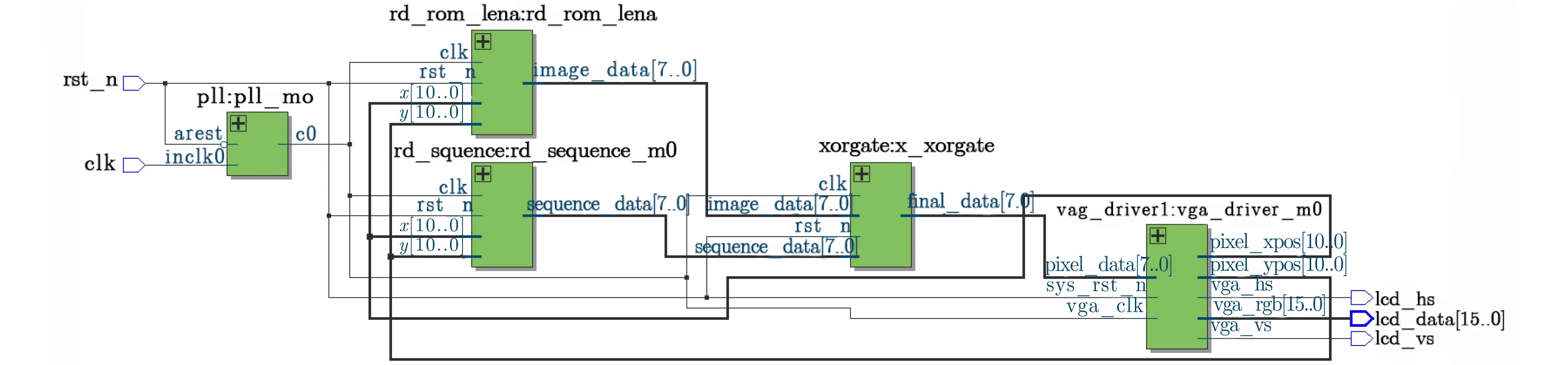
圖13 加密系統RTL圖

解密系統的RTL圖與加密系統RTL圖類似，如圖14所示，在加密系統RTL圖中增加一次異或運算得出解密信號。圖14中的pixel_data為解密圖像信號。

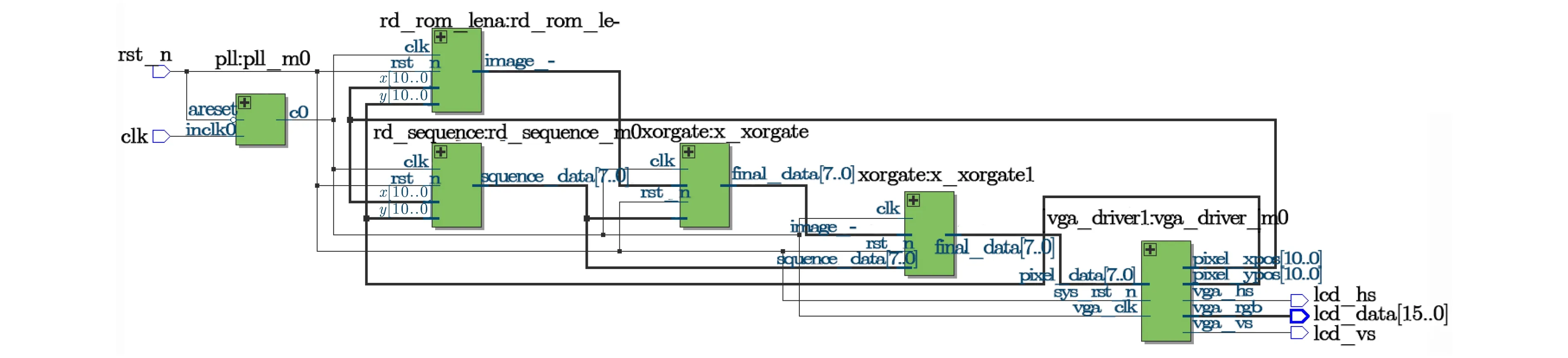
圖14 解密系統RTL圖

4.3 硬件實現加密時序圖分析

Quartus II具有嵌入式邏輯分析儀(signal tap)，它能方便地抓取模塊中的信號，方便開發者對各個信號的時序進行查看。本加密系統的Signal Tap圖由圖15所示。圖中a信號為原始圖像信號，b為密文圖像信號，c為解密后圖像信號。從圖15中可以看出，原始圖像信號和解密圖像信號完全相同，較好地實現了加密的效果。

圖15 Signal Tap時序圖

4.4 FPGA加密結果

基于FPGA的混沌加密結果如圖16所示。圖16所展示的為完整加密過程的FPGA實驗結果及VGA顯示圖。從圖中可以看出FPGA硬件實現的圖像結果與上文理論仿真一致，從而表明本文所提出的加密方案實際可行。

圖16 FPGA實驗結果VGA顯示圖

5 結束語

本文在經典的Logistic映射基礎上，引入非線性正弦反饋從而構建得到一種新的混沌系統。基于新的混沌映射，產生混沌加密序列，并對混沌加密序列先進行處理增強其偽隨機性，再進行數字圖像的加密運算。利用NIST測試組件對混沌加密序列的偽隨機性進行測試。數值仿真結果可見，本文所提出的新的數字圖像加密算法能夠較好地實現數字圖像加密，具有密鑰空間大、加密安全性高、計算簡單等特點。在FPGA中，該加密方法也能得到較好的實現。