基于光滑粒子法的某大口徑火炮不同膛線彈丸擠進過程研究
郭俊行,劉 琦,丁宏民,徐 堅,孫玉杰
(西北機電工程研究所,陜西 咸陽 712099)
彈帶擠進過程中彈帶材料受到膛線作用形成刻槽,發生劇烈塑性變形,發射時賦予彈丸轉速。傳統內彈道理論一般忽略擠進過程,而實際上是內彈道過程的一個階段,合適的擠進阻力對彈道一致性比較有利,而擠進阻力又受結構、材料和其他因素的影響[1]。文獻[2]使用有限元軟件LSDYNA仿真了某大口徑榴彈炮彈帶擠進過程,獲得了彈帶材料的應力三軸度與Lode角參數云圖,文獻[3]使用有限元軟件ABAQUS建立了擠進過程的非線性動力學模型,對彈帶擠進過程進行了數值模擬,但以上方法尚未應用于大口徑火炮彈丸膛內運動研究。文獻[4-5]基于有限元法(finite element method,FEM)與光滑粒子流體動力學(smoothed particle hydrodynamics,SPH)法建立彈丸擠進過程計算模型,文獻[6]使用SPH法對35 mm彈丸軟鐵彈帶擠進身管過程進行了仿真研究,文獻[7]使用SPH-FEM耦合方法研究了某大口徑火炮的彈丸擠進過程及彈丸膛內運動,說明基于SPH法建立彈丸擠進過程計算模型能夠較好地平衡精度和效率,具有一定的應用價值。
使用一般實體單元仿真大變形塑性問題時容易產生單元畸變,導致計算提前終止[8]。SPH作為一種無網格方法獲得了廣泛應用[9-10],它使用任意分布的粒子離散求解域,節點之間沒有網格聯接,不存在網格畸變問題,能較好地處理大變形問題。已經有學者使用光滑質點動力學法求解了大口徑火炮的擠進過程,但是對于擠進過程中材料是否失效還有待研究,在FEM中設置延性斷裂參數可能僅僅是為了使仿真能夠進行下去。材料的塑性、損傷與斷裂理論[11-12]是一個跨學科、多尺度、非線性極強的復雜問題,尚沒有統一的理論[13]。眾多研究表明金屬材料發生韌性斷裂之前發生塑性變形,受應力三軸度、Lode參數等的影響[14-15],孫全兆等、王鵬等和文獻[16]研究了彈丸擠進過程中彈帶材料應力三軸度和Lode參數等的變化,但沒有解釋材料是否發生失效。
綜上所述,對于大口徑火炮彈帶擠進過程中的塑性變形研究較少,特別是對應力、應變、溫度和損傷變量的分布缺乏研究,同時對于不同膛線纏度時的對比研究更少。工程實踐表明大口徑火炮的膛線形式對射擊精度和身管壽命有重要影響,有必要開展膛線形式對彈帶擠進過程影響研究。
1 仿真模型及邊界條件
建立了某大口徑火炮身管和彈丸的三維有限元模型,其剖面如圖1所示,等齊膛線纏度為20、混合膛線起始纏度為50,分別建立有限元模型。該火炮發射的底凹榴彈有前后兩條彈帶,為了節省計算資源將彈帶分成兩部分建模,內層變形較小使用FEM建模,外層變形較大使用SPH建模,內外層之間建立綁定約束。在彈帶光滑粒子單元、彈丸前定心部外表面和內膛表面之間建立接觸關系。

圖1 某大口徑火炮和彈丸的三維有限元網格
由于彈帶與膛線的相互作用涉及大變形,研究中采用Johnson-Cook屈服模型描述材料應變硬化、應變速率強化、溫度軟化行為。Johnson-Cook材料模型中屈服應力是塑性應變、應變率以及溫度的函數
(1)
T*=(T-Tr)/(Tm-Tr)
(2)
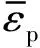
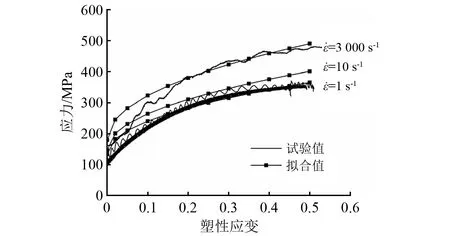
圖2 不同應變速率時H96黃銅應力隨塑性應變變化曲線
材料塑性變形中溫度升高由式(3)計算
(3)
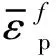
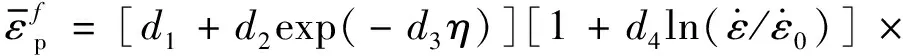
(1+d5T*)
(4)
式中:η為應力三軸度;d1~d5為失效參數,分別為0.540,4.890,3.030,0.014,1.120。
材料的失效由下面的塑性應變累積準則來判斷
(5)
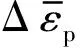
除了彈帶部分,其余結構均設為線彈性材料,分別賦予材料屬性。擠進過程時間短,屬于高速沖擊問題,時間太短熱量來不及擴散,建立帶絕熱分析的顯式動力學分析步,能夠獲得材料變形時的溫度。彈帶材料的初始溫度設為20 ℃。該大口徑火炮采用某種模塊裝藥方案時以全裝藥、藥溫常溫、發射底凹榴彈時內彈道計算得到的彈底壓力曲線,如圖3所示,以壓力曲線形式加載于彈丸底部。
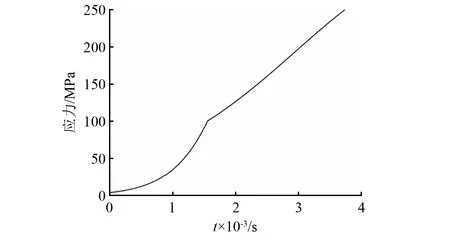
圖3 彈底壓力曲線
2 模型計算結果
混合膛線時用等效塑性應變分布表示的變形過程,如圖4所示,可以看出在擠進過程中隨著燃氣壓力逐漸增大,彈丸逐漸向前運動擠入炮膛,彈帶材料受到膛線作用,發生劇烈塑性變形形成刻槽。從圖4中可知,前后彈帶幾乎同時開始發生塑性變形,到2.4 ms時前彈帶擠進完成時后彈帶凸起才開始發生明顯的變形,可見在陽線的作用下形成刻槽,在3.2 ms后形成完整刻槽,塑性變形不斷增大,局部最大等效塑性應變可達1.7。
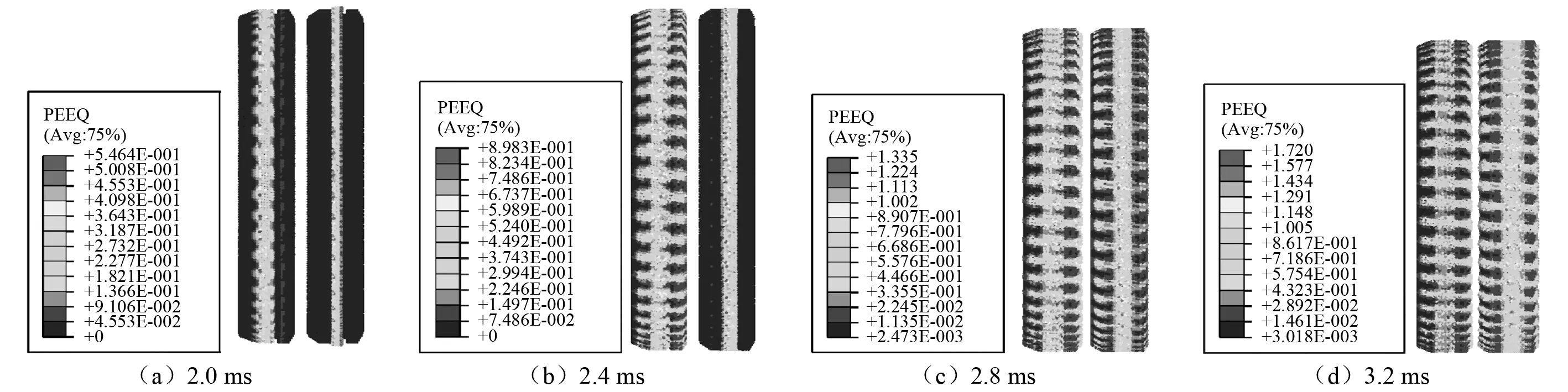
圖4 仿真得到的混合膛線時彈帶擠進變形過程
仿真得到的彈丸運動加速度、速度、位移曲線,如圖5所示。可見隨著壓力增加彈丸加速度、速度、位移不斷增大最終擠入炮膛,與內彈道給出的結果略有差異。本文以彈帶全部進入完整膛線為擠進完成,兩種工況時彈丸位移都是107 mm,等齊膛線工況下擠進完成時刻、加速度、速度分別為3.18 ms,78 800 m/s2和108 m/s,混合膛線工況下擠進完成時刻、加速度、速度分別為3.17 ms,79 600 m/s2和109 m/s。
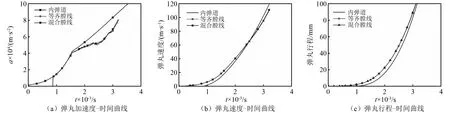
圖5 經典內彈道計算結果與仿真結果對比
仿真得到的擠進過程中彈帶受的沿軸向的阻力變化,如圖6所示。從圖6中可以看出在彈丸行程6 mm、時間2.5 ms以前擠進阻力一直在增大,等齊膛線和混合膛線的最大擠進阻力分別為850 kN和790 kN;而后開始減小并有所波動,在彈丸行程為100 mm、時間為3.17~3.18 ms時擠進完成。本文仿真的工況與孫全兆的研究背景、試驗工況如膛壓、初速等較為接近,本文計算出的擠進完成時刻彈底壓力、擠進終了時刻彈丸速度、最大擠進阻力和孫全兆的實測數值較為接近,說明本文建立的數值仿真模型具有較高的仿真精度,能夠精確的刻畫出擠進過程。

圖6 仿真得到的擠進阻力曲線
仿真得到的彈丸所受的力矩,如圖7所示。由圖7可見導轉力矩有波動,前彈帶擠入時導轉力矩逐漸上升至50 000 N·m(等齊膛線)和23 600 N·m(混合膛線),在后彈帶擠入時先下降再次上升,可以看出等齊膛線時導轉力矩波動較大。這是因為前彈帶嵌入過程中彈丸已經獲得了轉速,而后彈帶以一定的轉速撞在膛線上,從而引起了力矩波動,說明雙彈帶結構在膛線起始纏角大時擠進變形不夠協調,在起始纏角小時相對平穩。
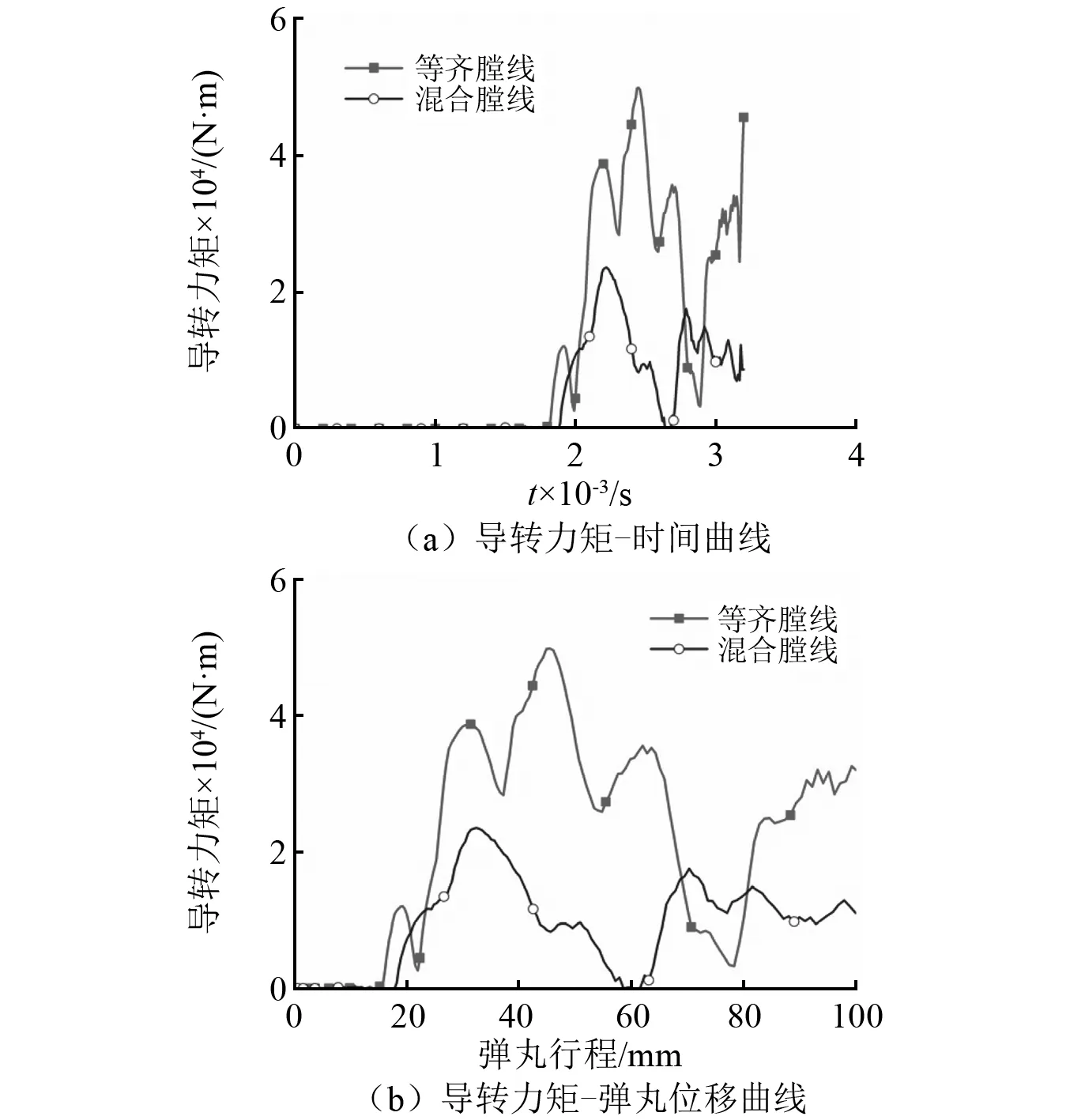
圖7 仿真得到的導轉力矩曲線
擠進完成時彈帶的等效應力、等效塑性應變、溫度、損傷變量分布如圖8、圖9所示。局部等效應力分別可達1 093 MPa(等齊膛線)、652.5 MPa(混合膛線),等效塑性應變可達1.651(等齊膛線)、1.735(混合膛線),溫度可達240 ℃(等齊膛線)、254 ℃(混合膛線),損傷變量局部達到1.0。圖中可以看出等效應力和損傷變量分布較為均勻,塑性應變和溫度的分布不均,形成刻槽的部分塑性變形大且溫度升高明顯。

圖8 仿真得到的等齊膛線時等效應力、等效塑性應變、溫度、損傷變量分布

圖9 仿真得到的混合膛線時等效應力、等效塑性應變、溫度、損傷變量分布
3 統計分析
由于后處理器功能的限制,圖4、圖8、圖9的顯示效果較差,采用二次開發編程從輸出結果中讀取所有粒子單元的坐標、應力分量、等效塑形應變、溫度和損傷變量等,并統計粒子分布如圖10所示。從圖10可以看出多數外層的彈帶材料等效應力分布在200~600 MPa、應力三軸度小于1,說明以壓縮變形為主少數受拉;而羅德參數在從-1~1,分布較為均勻,說明材料受到剪切作用,這與彈帶功能相一致;等效塑性應變小于1.0、溫度低于150 ℃、損傷變量值小于0.2的粒子占了大部分,說明彈帶材料在承受劇烈塑形變形的同時沒有發生顯著的斷裂,可以認為整個過程是塑性變形為主。其中羅德參數定義為
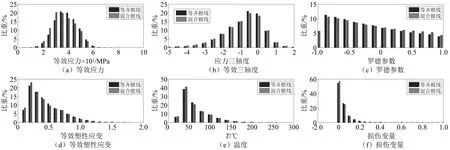
圖10 仿真得到的外層彈帶粒子單元數量分布
(6)
式中:J3為偏應力第三不變量;σeq為等效應力。J3和σeq可參考Nahshon等的研究。
4 光滑粒子單元后處理方法及結果討論
圖4、圖8、圖9是擠進完成后某些彈帶粒子的分布,從圖中可知現階段的后處理技術難以反映出彈帶形狀,不能較好的表示出變量分布。以身管軸線某一點為原點建立坐標系,身管指向設為z軸正向,以向左為x軸正向,向上為y軸正向,如圖11所示。從合膛圖上能夠做出擠進后彈帶的假想三維結構圖,定義橫切面和縱切面,以等齊膛線工況為例當擠進完成后它們之間的相對關系,如圖11(a)、圖11(b)所示。

圖11 坐標系定義和自定義截面
在用二次開發編程從輸出結果中讀取所有粒子單元的坐標、應力分量、等效塑形應變、溫度和損傷變量的基礎上,本文提出了一種新的后處理方法,它使用核函數進行插值、繪圖等得到某個截面上的變量分布。前后彈帶中間橫截面的局部云圖,如圖12、圖13所示,其中彈丸旋轉方向為逆時針方向,橫軸和縱軸分布為該截面上的x、y坐標。
等齊膛線的前彈帶中間橫截面處局部云圖見圖12。從圖12中可知最大等效應力約300 MPa、最大等效塑性應變約0.5、最高溫度約60 ℃、最大損傷變量值達到0.1,處于陽線下方,總體上分布不均勻,說明材料受陽線壓縮而發生塑性變形流動;在該截面上應力三軸度小于0,說明以壓縮變形為主,受到陽線擠壓部分的應力三軸度較小;而ω參數最大值約0.5,說明彈帶材料受到了剪切作用,這與彈帶的功能一致。其中參數定義為

圖12 仿真得到的等齊膛線前彈帶切片(z=1 163 mm)
(7)
可見該方法能夠更好的查看光滑粒子內部區域的場變量分布和材料的幾何外形。
混合膛線時前彈帶中間橫截面處局部云圖見圖13。從圖13中可知局部最大等效應力約300 MPa、最大等效塑性應變約0.4、最大溫度升高約60 ℃、最大損傷變量值達到0.05,處于陽線下方,總體上分布較均勻,也是以壓縮變形為主、也受到了剪切作用。不同于等齊膛線時的工況,導轉側和非導轉側的變量分布差異不大,說明混合膛線時擠進過程較為平穩,有利于減少導轉側磨損從而提高身管壽命。

圖13 仿真得到的混合膛線前彈帶切片(z=1 163 mm)
使用自主開發的后處理程序得到了彈帶縱向切片上等效應力分布云圖,如圖14、圖15所示,炮口方向沿z軸正向。受火炮膛線纏角的影響,在等齊膛線時縱切面Ⅰ切在后彈帶上時近似在火炮陰線上、切在前彈帶上時近似在火炮陽線上;縱切面Ⅱ切在后彈帶上時近似在火炮陽線上、切在前彈帶上時近似在火炮陰線上。從圖中可以看出,在陽線下方彈帶的縱截面處等效應力較大。

圖14 仿真得到的等齊膛線時彈帶縱向切片上等效應力分布
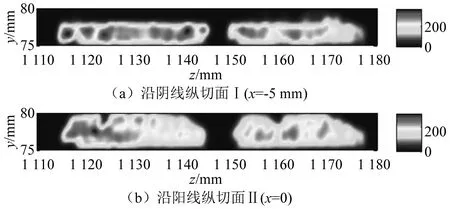
圖15 仿真得到的混合膛線時彈帶縱向切片上等效應力分布
5 結 論
本文使用光滑粒子法仿真了某大口徑火炮分別采用等齊膛線(纏度20)和混合膛線(起始纏度50)以全裝藥發射底凹榴彈的擠進過程,得到了彈帶所受軸向阻力和導轉力矩及等效應力等分布。主要結論有:
(1)仿真結果表明起始纏角增大時擠進阻力增大,前彈帶擠入時導轉力矩逐漸上升而在后彈帶擠入時先下降再次上升,且起始纏角大時導轉力矩波動較大。雙彈帶結構在纏角大時擠進變形不夠協調,而在小纏角時相對平穩。
(2)統計結果表明擠進過程中多數粒子的等效塑性應變小于1.0、溫度低于150 ℃、損傷變量小于0.2,說明彈帶材料在承受劇烈塑性變形的同時溫度升高但沒有發生宏觀斷裂。
(3)使用主開發的后處理程序得到了彈帶橫截面、縱向截面上等效應力等云圖,結果表明材料以壓縮變形為主、也受到了剪切作用,膛線起始纏角小時導轉側和非導轉側的變量分布差異較小,說明采用雙彈帶結構時減小起始纏角可以使擠進過程更平穩,有利于減少導轉側磨損從而提高身管壽命。

