主余震型地震動過程的降維模擬

姜云木，阮鑫鑫，劉章軍

(武漢工程大學 土木工程與建筑學院，武漢 430074)

地震災害具有很強的破壞性與隨機性，同時在一次主震后往往會伴隨著多次余震的發生，且余震對結構造成的二次破壞不容忽視。由于主余震序列地震動記錄數量有限以及對具體場地條件的限制，無法滿足對結構計算的需求，因此，主余震型地震動的人工模擬備受關注。

建立合理的主余震地震動參數之間的關系，是精細模擬主余震型地震動的前提。相對于主余震復雜的震源機制等因素，工程師更關注主余震地震動的幅值、持時與頻譜等工程特性的關聯。在早期的研究中，學者們主要對主余震之間的峰值加速度、持時等參數關系進行了初步探索[1-3]。近年來，Zhang等[4]利用線性合成法擬合了主余震間震級、持時、能量等參數的關系。隨后，Muderrisoglu等[5]估計了主震后一段時間內發生超越特定震級閾值的余震概率。此外，朱瑞廣等[6]通過Copula函數較為完整地分析了主余震強度參數的相關性。Ruiz-Garcia等[7]研究發現：主震的場地卓越圓頻率比余震的場地卓越圓頻率有偏小的趨勢，且具有中等的相關性。上述研究表明，主余震參數之間存在一定的相關性，但從工程實用角度來看仍需進一步的研究。

主余震型地震動的構造方法可分為確定方法和隨機方法兩大類。在確定方法方面：Hatzigeorgiou等提出了重復法來構造主余震序列，該方法假設主余震的特性一致，這顯然不符合實際情況；Li等[8]提出了隨機組合法構造主余震序列，即從主余震記錄庫中分別隨機挑選出一條地震動記錄組合成主余震序列，但該方法本質上得到的主余震序列不具有隨機性。在隨機方法方面：Hu等[9]首先利用調幅過濾白噪聲方法生成主震，再利用分支序列法生成余震，但是該方法并沒有考慮主余震間的條件關系與衰減關系；Nithin等[10]基于Priestley理論，提出了一種基于主震的余震條件縮放模型，并結合特定的場景生成了主余震時程樣本。然而，該方法在本質上屬于蒙特卡洛方法，為了保持模擬精度，需要成千上萬的隨機變量，導致了模擬時生成的樣本數量龐大以及概率信息不完備的問題。綜上所述，亟需建立一種能考慮主震與余震相互關聯且高效實用的模擬方法。

基于上述研究進展，筆者首先在非平穩地震動過程的演變功率譜密度模型的基礎上，對實測主余震記錄的峰值加速度、場地土的卓越圓頻率、阻尼比以及調制函數參數進行識別。然后，通過擬合優度檢驗，給出最優邊緣分布和最優Copula模型。在此基礎上，得到了主震參數條件下對應余震參數的條件均值。最后，結合譜表示-隨機函數方法[11]，建立了主余震型地震動的降維模型，實現了主余震型地震動的高效模擬。此外，本文建立了主余震參數之間的實用計算公式，方便了工程應用。

1 時-頻全非平穩模型參數的識別

1.1 非平穩地震動過程的演變功率譜密度模型

相對于震級和震源機制的地震學因素和“震源-傳播途徑-局部場地”的物理模型，地震工程更加關注地震動本身的幅值、持時與頻譜等工程特性。因此，本文選用工程中經典的演變功率譜密度模型，該模型從地震動的頻譜特性出發，能夠反映地震動過程的非平穩性和統計特性。同時，通過建立主余震演變功率譜參數之間關系，可以方便地體現地震動的序列性。

根據非平穩隨機過程的Priestley演變譜理論，非平穩地震動加速度過程的演變功率譜密度函數可表示為[12]

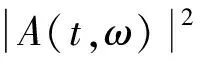
(1)

式中:SUg(t,ω)為非平穩地震動加速度過程Ug(t)的單邊演變功率譜密度函數；A(t,ω)為時-頻調制函數；S(ω)為平穩地震動加速度過程的單邊功率譜密度函數。

對于時-頻調制函數，采用Deodatis等[13]提出，劉章軍等[14]改進的模型

其中,

(3)

式中:參數b=a+0.001;c=0.005；a為控制地震動過程衰減快慢的參數，s-1。一般地，a越大，地震動過程衰減越快。

對于平穩地震動加速度過程的單邊功率譜，采用Clough-Penzien模型[15]

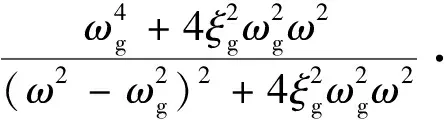
(4)

式中:ωg和ξg分別為場地土的卓越圓頻率和阻尼比；ωf和ξf分別為基巖的卓越圓頻率和阻尼比。一般地，可取ωf=0.1ωg，ξf=ξg。

在式(4)中，譜強度因子S0可表示為

(5)

式中:Amax為地震動峰值加速度的均值；r為峰值因子，在進行參數識別時取r=3。

1.2 演變功率譜密度模型的參數識別

由1.1節提出的時-頻全非平穩模型可知，演變功率譜密度模型的參數向量可以表示為λ，即λ=[ωg,ξg,a]。需要指出的是，在進行場地土的卓越圓頻率和阻尼比識別時，對實測強震加速度記錄進行了調幅，因此參數向量λ中不包含地震動峰值加速度均值Amax和峰值因子r。于是，可定義演變功率譜密度模型的頻域能量分布函數E(ω;λ)如下[16]

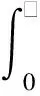
(6)

將式(1)和式(2)代入式(6)，積分可得本文模型對應的頻域能量分布函數

E(ω;λ)=

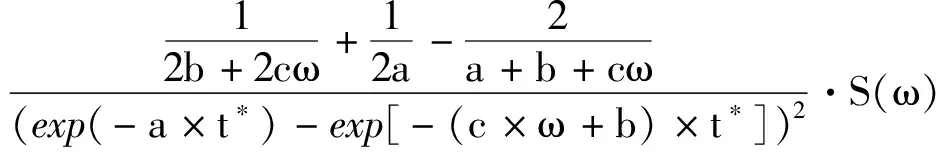
(7)

記第i條實測記錄的演變功率譜為Sug,i(t,ω)，如果放松演變功率譜的能量隨時間分布再取其平均，那么對于第i條實測記錄，可以得到其等價平穩過程的功率譜的函數Si(ω)如下[17]

(8)

由式(8)可得，第i條實測記錄的頻域能量分布函數Ei(ω)為

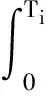
(9)

式中：Ti為第i條地震動記錄的總持續時間；T0,i為第i條地震動記錄的強震持時，具體可表示為[18]

(10)

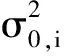
(11)

(12)

式中:ai(t)為第i條實測地震記錄時程；ωu,i為第i條實測地震記錄時程的上限頻率。

當取得一條地震動實測記錄時，可以通過信號處理的方法得到實測記錄的平穩功率譜Si(ω)，再根據式(9)與式(10)即可得到第i條實測記錄的頻域能量分布函數Ei(ω)。

根據主余震實測記錄得到的頻域能量分布函數曲線，采用最佳平方逼近準則，針對每條曲線分別識別參數向量λ

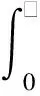
(13)

本識別方法原理簡單，利用簡單的頻域能量相等原理，避免了在時頻域上參數識別的困難，減少了計算量。且編程簡單，僅需要3個主要的MATLAB工具箱函數便可以實現。

1.3 實測地震動記錄的識別結果

本文在太平洋地震動工程研究中心的NGA-West2地震動數據庫中嚴格按照以下原則[19]篩選地震波：

(1)主震記錄與其對應的余震記錄必須來自同一臺站。

(2)余震只選取與主震對應且震級最大的余震作為研究對象。

(3)斷層距離應大于10 km，以減少近斷層效應的影響。

(4)主余震的震級應該均大于5，排除對結構影響不大的地震動。

經過嚴格篩選得到了17次地震的468組地震動記錄。表1給出了本文所采用17次地震的地震名稱、臺站數量、震級、斷層距范圍和VS,30范圍等基本信息。

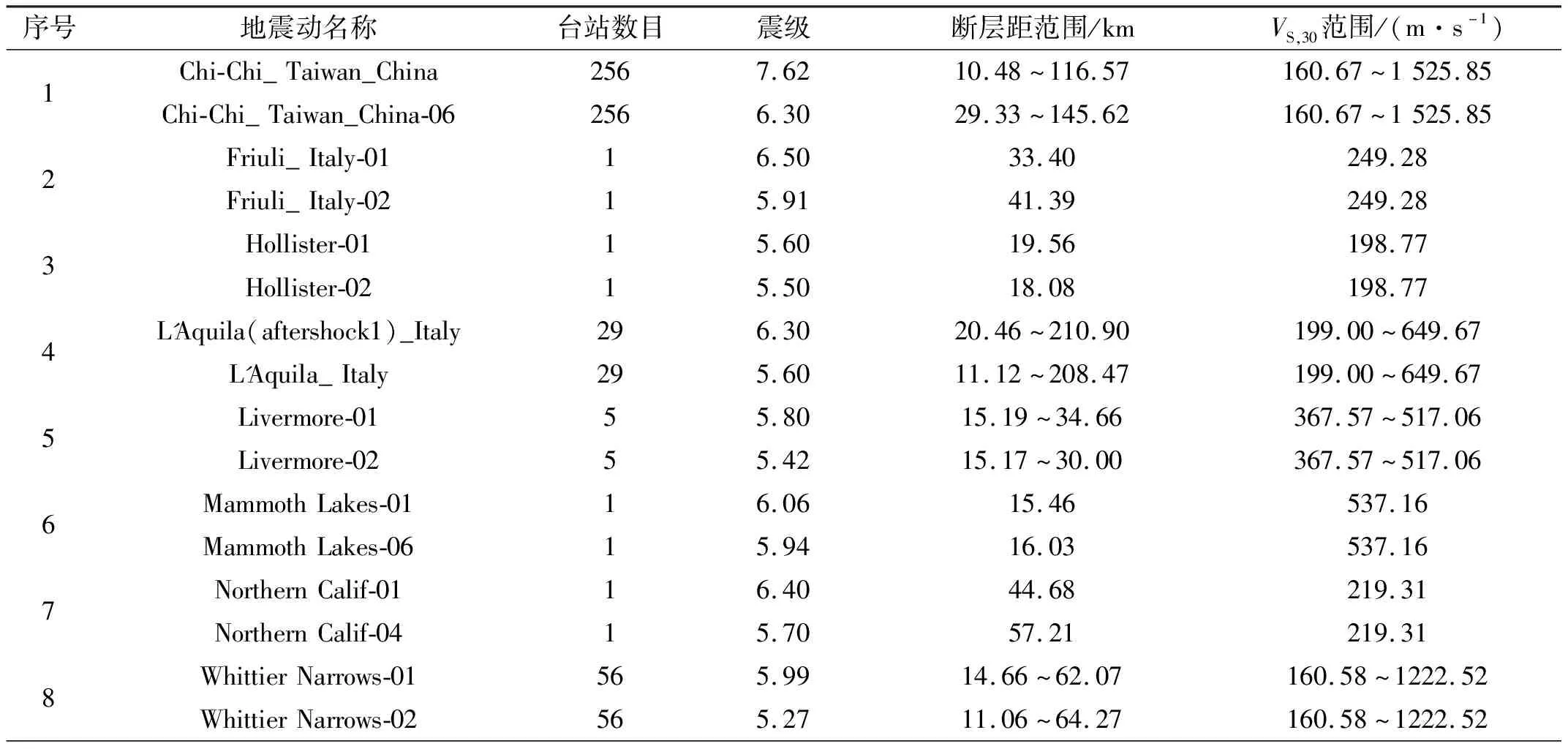
表1 本文選取地震動記錄的詳細信息

本文根據GB 18306—2015《中國地震動參數區劃圖》[20]中建議的5種場地類別對實測強震記錄進行篩選。為了將國外的實測記錄與國內的場地類別相結合，眾多學者研究建立了《中國地震動參數區劃圖》中場地類別與剪切波速VS,30的對應關系[21]。在本文中，采用文獻[22]的場地劃分標準。表2給出了不同場地類別對應的剪切波速VS,30范圍與篩選得到的實測強震記錄的數量。

表2 場地類別與VS,30的對應關系

對468組主余震加速度記錄進行基線校正，并將峰值加速度調幅到200 cm/s2，利用1.2節的識別方法按照場地類別依次對演變功率譜密度模型的參數向量λ進行識別。

以CHY057臺站分別觀測的Chi-Chi地震主震和余震為典型實例。圖1(a)和圖2(a)分別給出了典型實例的主余震的實際能量曲線與模型能量曲線的對比，由圖1(a)和圖2(a)可知，模型能量分布曲線與實測記錄的能量分布曲線擬合效果較好。同時，圖1(b)、圖1(c)、圖2(b)、圖2(c)給出了本文選取所有的II類場地主余震實測能量曲線與模型能量曲線的均值和標準差對比。可以看出，主余震模型能量曲線的均值及標準差與實測記錄對比效果良好，充分說明了本文參數識別方法的有效性。

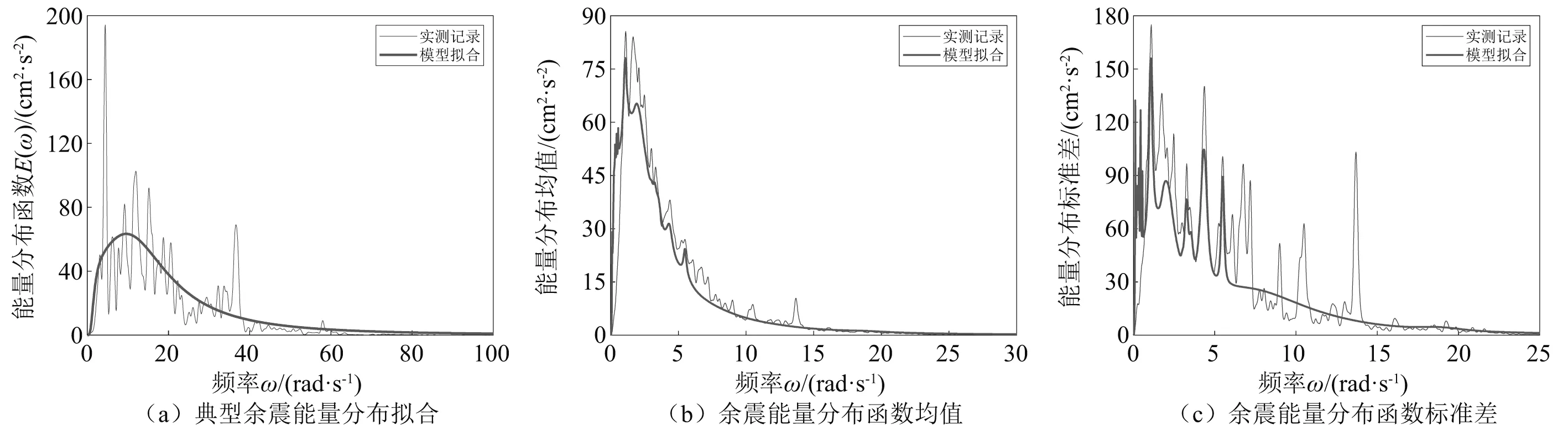
圖2 余震能量擬合曲線

2 主余震參數的最優邊緣概率分布

在本文中，除了對主余震記錄的場地參數，即參數向量λ進行識別外，還提取主余震地震動實測記錄的峰值加速度PGA。這樣，考慮主震和余震，一共需要估計8個地震動參數的邊緣概率密度分布。需要指出的是，提取主余震的峰值加速度未考慮場地類別，且均來自468組地震動記錄調幅之前的統計結果。

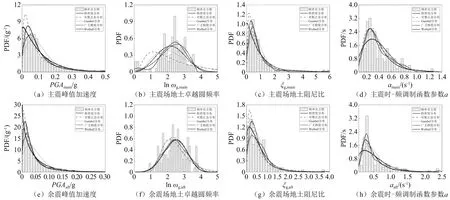
圖3 主余震地震動參數概率密度函數

在主余震參數的邊緣分布參數識別完成后，需要采用AIC信息準則(akaike information criterion)判斷最優的邊緣分布模型。AIC值的定義如下[24]

AIC=2k-2lnL

(14)

式中:k為分布模型中參數的個數;L為模型最大似然函數。一般地，AIC值越小，代表模型擬合度越好。

通過AIC信息準則判斷，并可得到主余震參數的最優邊緣分布以及模型參數,如表3所示。當概率模型為對數正態分布時，Par1為均值，Par2為標準差；為Gumbel分布時，Par1為位置參數，Par2為形狀參數；為廣義極值分布時，Par1為形狀參數，Par2為尺度參數，Par3為位置參數；為Weibull分布時，Par1為比例參數，Par2為形狀參數。

表3 主余震時域參數與場地參數概率模型

3 基于Copula理論的主余震參數相關性分析

3.1 基本理論

Copula函數可以看作是一類聯結聯合分布函數和邊緣分布函數的“紐帶”，它描述了多維隨機變量之間的相關性。根據Sklar定理[25]，二維隨機變量(X1,X2)的聯合分布函數F(x1,x2)及其邊緣分布可寫成如下形式

F(x1,x2)=C(F1(x1),F2(x2))=C(u1,u2)

(15)

式中:FXi(xi)(i=1,2)為隨機變量Xi的邊緣概率分布函數;C(·)為Copula分布函數。于是，二維隨機變量(X1,X2)的聯合概率密度函數可以表達為

f(x1,x2)=c(u1,u2)fX1(x1)fX2(x2)

(16)

式中：fXi(xi)(i=1,2)為隨機變量Xi的邊緣概率密度函數；c(·)為Copula密度函數，即

(17)

若將主震的某一參數(例如，場地土的卓越圓頻率)視為隨機變量X1，與其對應的余震參數視為隨機變量X2，則在給定主震參數的條件下對應余震參數的概率密度函數可表達為

鼓粒成熟期是大豆積累干物質最多的時期，也是產量形成的重要時期。促進養分向子粒中轉移，促粒飽增粒重，適期早熟則是這個時期管理的中心。這個時期缺水會使秕莢、秕粒增多，百粒重下降。秋季遇旱無雨，應及時澆水，以水攻粒對提高產量和品質有明顯影響。大豆黃熟末期為適收期。當種子含水量達到13%時可以入庫。

(18)

進一步地，條件均值可以表達為

(19)

從式(19)可知，在確定了主余震參數的邊緣分布以及Copula函數之后，通過給定主震參數的取值，就可以得到該條件下的對應余震參數的取值。

3.2 最優Copula函數的選擇

在選擇主余震參數的最優Copula函數之前，需采用Kendall秩相關系數判斷參數相關性的大小。Kendall秩相關系數τ可由式(20)計算[26]

(20)

式中：x1，i和x2,i分別為主震和余震地震動參數的第i個觀測值；N為樣本容量;sign[·]為符號函數，當(x1,i-x1,j)(x2,i-x2,j)>0時，sign=1，否則sign=0。

主余震參數的Kendall相關系數,如表4所示。需要說明的是，由于Ⅰ0和Ⅳ類場地的實測記錄數量較少，故沒有分析其相關性。從表4中可以看出主余震的PGA之間保持著中等相關性，場地參數除了場地阻尼比之外保持著中等相關性。盡管主余震場地阻尼比ξg之間趨近于獨立，但是筆者同樣發現不同場地余震的場地土卓越圓頻率ωg,aft和阻尼比ξg,aft之間均保持著中等負相關性(見表4)，因此可以采用Copula函數分析ωg,aft與ξg,aft的相關性。

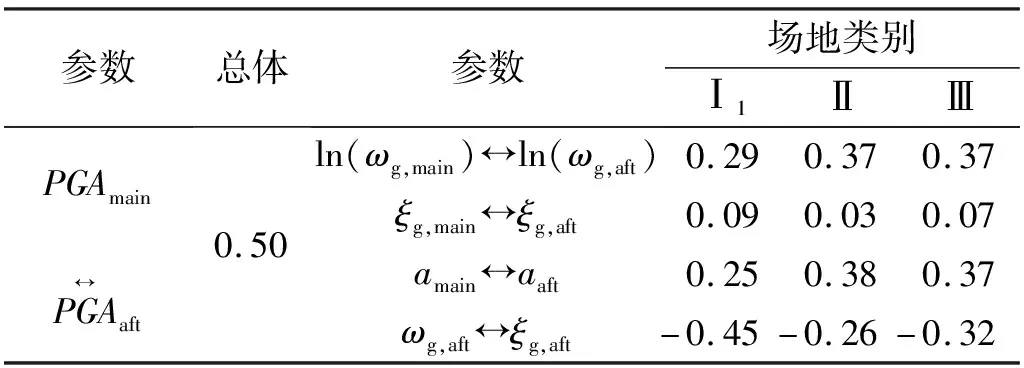
表4 主余震參數之間的Kendall秩相關系數

根據主余震的參數之間的相關特性，本文采用6種Copula函數對主余震對應的峰值加速度、場地土卓越圓頻率和調制函數參數以及余震的場地土卓越圓頻率與阻尼比之間的相關結構進行擬合，對參數間的正負相關性和各種尾部相關性要求至少有一種Copula函數能描述。這6種Copula函數及其特征分別為：Gumbel Copula(具有上尾相關性，適合描述兩個變量同時上漲的情況)、Clayton Copula(具有下尾相關性，適合描述兩個變量同時下降的情況)、Frank Copula(可以同時擬合上、下尾相關且可以同時描述變量正相關性與負相關性)、Plackett Copula(對變量間相關性的正負無要求)、AMH Copula(對正負相關性無要求，但是不適合高相關性情況分析)和FGM Copula(為Plackett Copula關于(η-1)的泰勒展開式的前兩項)。Copula函數的具體分布函數及其參數η,如表5所示。

表5 備選Copula函數模型[27]

對以上6種備選Copula函數同樣進行AIC信息準則檢驗，即可選擇出最優模型，檢驗的具體結果和最優Copula參數η，如表6所示。可以看出，PGA、場地參數ωg和時-頻調制函數參數a的最優Copula模型以Plackett Copula為主；ωg,aft與ξg,aft的最優Copula模型同樣以Plackett Copula為主。

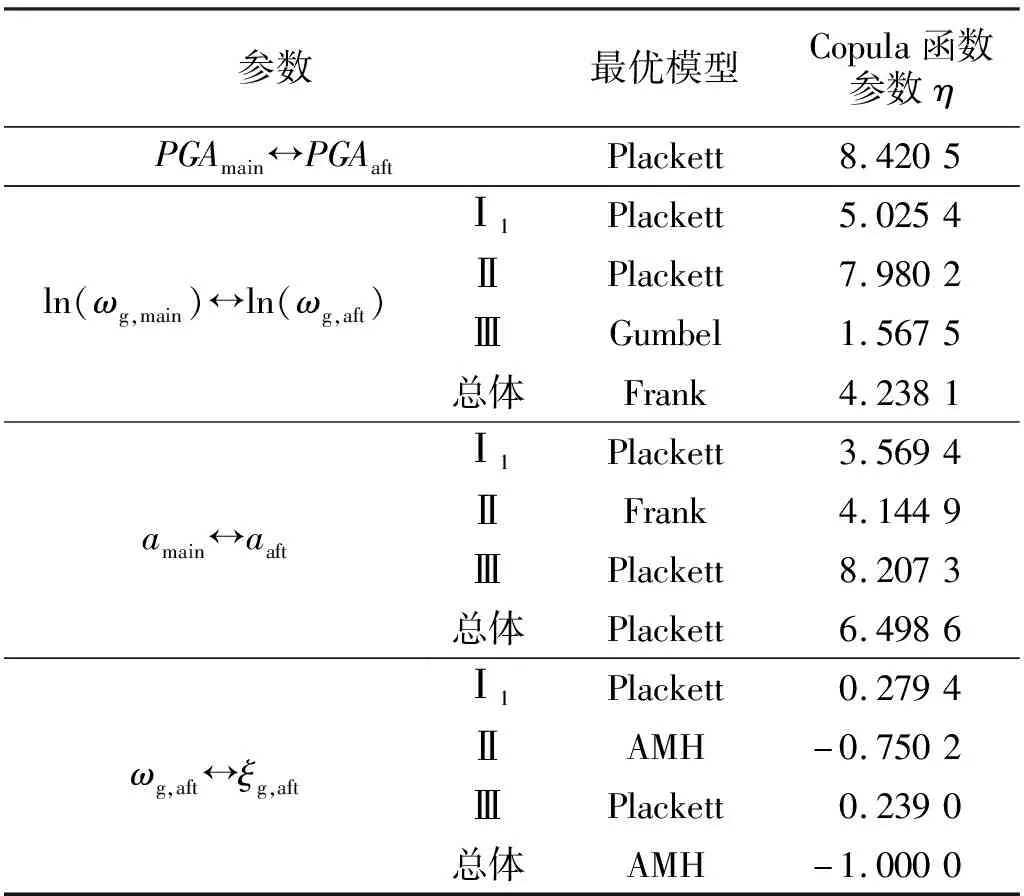
表6 最優Copula模型

3.3 余震參數的條件概率密度函數與條件均值

在確定了主余震參數的邊緣分布以及主余震參數之間的最優Copula函數之后，由式(16)～式(19)可得在主震參數條件下余震的條件概率密度函數和條件均值。不同主震峰值加速度條件的余震峰值加速度的概率密度函數和邊緣概率密度的對比，如圖4所示。由圖4可知，在不同主震參數影響下，對應余震參數的概率密度函數區別顯著，因此可以證明，考察余震參數時有必要考慮主余震參數之間的相關性。

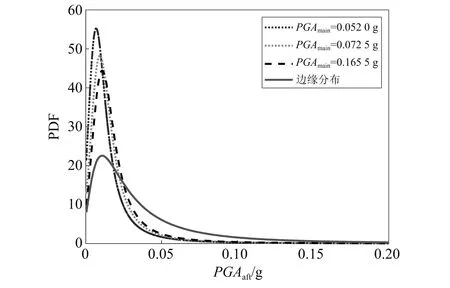
圖4 不同主震峰值加速度下的余震峰值加速度的概率密度函數對比

條件均值與觀測值的對比圖，如圖5所示。由圖5可知，Copula條件均值能夠反映出給定主震參數條件下，余震參數的總體趨勢。因此，可以利用Copula條件均值預測給定主震參數條件下余震參數的取值。

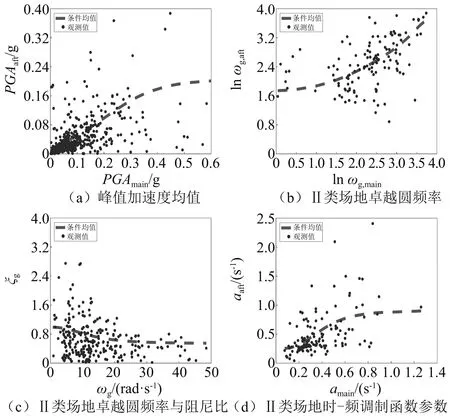
圖5 Copula條件均值與觀測散點圖對比

在本文中，對主余震參數的條件均值曲線進行了最高8次的多項式擬合，得到了主余震參數的衰減關系式。表7中給出了Copula條件均值多項式擬合系數，其中，PGAmain和PGAaft的單位為g；ωg,main和ωg,aft的單位為rad/s；amain和aaft的單位為s-1。由于Ⅰ0類場地與Ⅳ類場地數據較少，因此不對這兩類場地進行Copula均值計算，但是本文對總體記錄的場地參數進行了分析并進行了多項式擬合來彌補這個問題。由此便建立了主余震參數之間的衰減關系，通過給定一套主震參數，便可以得到一套對應余震參數，這為工程應用提供了方便。

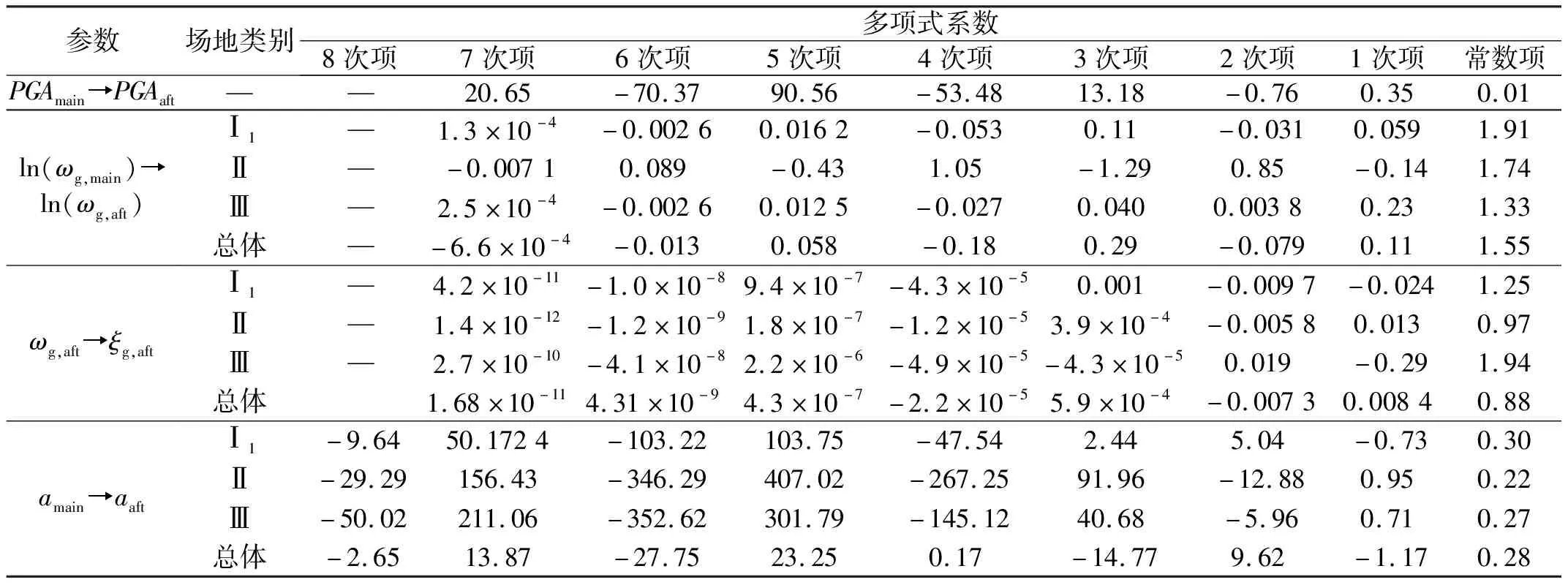
表7 Copula條件均值的多項式擬合系數

4 主余震型地震動過程的降維表達

4.1 非平穩地震動過程的降維表達

對于一個演變功率譜密度函數為SUg(t,ω)的零均值實非平穩地震動過程Ug(t)，其源譜表示為

(21a)

(21b)

式中:Δω為頻率步長，Δω=ωu/N，ωu為截斷頻率，N為截斷項數;{Xk,Yk}為一組標準正交隨機變量，滿足如下基本條件

E[Xk]=E[Yk]=0，E[XjYk]=0

(22a)

E[XjXk]=E[YjYk]=δjk

(22b)

式中：E[·]為數學期望；δjk為Kronecker-delta記號。

在式(21)中，由于隨機變量Xk和Yk的概率分布未給定，因此不能直接用于模擬。定義正交隨機變量集{Xk,Yk}(k=1,2,…,N)為如下形式

(23)

式中，φk(k=1,2,…,N)為一組在(0,2π)上均勻分布且相互獨立的隨機相位角。顯然，式(23)定義的隨機變量集{Xk,Yk}(k=1,2,…,N)滿足基本條件式(25)。

將式(23)代入式(21a)中，即可得到非平穩地震動隨機過程的傳統隨機相位模擬公式

(24)

式中,Ug1(t)即為采用傳統隨機相位角的譜表示模擬過程。可以看出傳統模擬方法在本質上屬于經典的蒙特卡洛方法，面臨著高維隨機變量所帶來的巨大挑戰。為了克服傳統蒙特卡洛方法隨機變量數量過大，模擬效率低下的缺陷，引入隨機函數的降維思想[28]，將標準正交隨機變量集{Xk,Yk}(k=1,2,…,N)定義為基本隨機向量的正交函數形式，具體如下

(25)

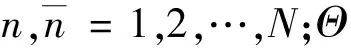
4.2 主余震序列的構造

在主余震型地震動過程的降維模擬中，主震地震動過程和余震地震動過程均采用1.1節中的演變功率譜密度模型，其主要區別在于模型參數的取值。通過給定的場地條件、地震烈度，確定主震的峰值加速度和持時。對于主震的場地土卓越圓頻率、阻尼比和調制函數，則根據場地類別采用參數識別結果的均值。進一步，利用表7的得到對應的余震參數，再把主震與余震的兩套參數代入式(2)、式(4)與式(1)中便可得到主震和余震的演變功率譜密度模型。

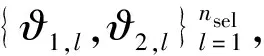
這樣，就實現了僅需兩個基本隨機變量即可精細的模擬主余震型地震動過程的目的。本文方法能夠有效避免傳統蒙特卡羅方法帶來的樣本數量龐大與樣本集合概率信息不完備的問題，僅僅需要數百條樣本即可在全概率層面上反映主余震型地震動過程的概率特性，具有與概率密度演化方法[30]結合的天然優勢。

5 算例分析與驗證

5.1 算例及分析

在本算例中，式(21)的計算參數為：頻率截斷項數N=1 600；截斷頻率ωu=240 rad/s；頻率步長：Δω=0.15 rad/s；時間步長：Δt=0.01 s；主震和余震的模擬持時分別取為20 s和15 s。主震和余震其他的地震動參數如表8所示。需要說明的是，表8中主震的峰值加速度考慮8度設防地震，主震場地卓越圓頻率、阻尼比和時頻調制函數參數取為II類場地主震參數識別結果的均值。對于表8中余震參數，是利用所得主震參數通過表7求得的。

表8 主余震地震動參數取值

圖6為用本文提出的方法模擬的Ⅱ類場地的主余震代表性時程曲線及模擬的144條主余震地震動過程代表性樣本的均值及標準差與相應目標值的比較結果。從圖6可以看出，余震衰減比主震更快，包含的能量更小，且144條代表性樣本集合的模擬結果均與目標值擬合較好，這充分說明了本文方法的有效性。

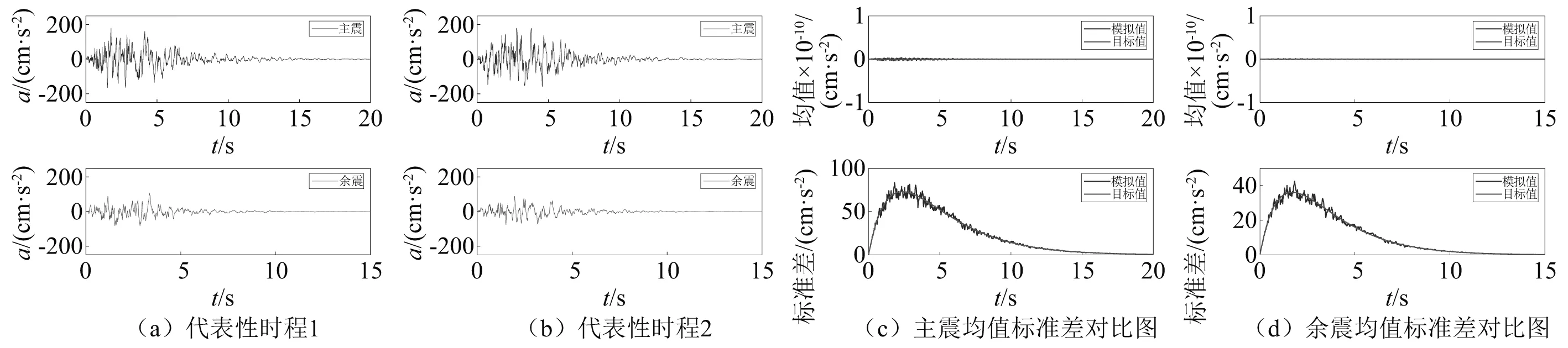
圖6 主余震代表性樣本以及樣本集合均值和標準差

5.2 主余震頻譜特征驗證

在本節中，將本文模擬方法得到的144條Ⅱ類場地的主余震代表性樣本與篩選得到的主余震實測地震動記錄對比。為方便起見，將模擬得到的余震時程與主余震實測記錄均調幅至200 cm/s2。計算Ⅱ類場地的實測地震動記錄的加速度反應譜與傅里葉幅值譜，并同本文的模擬結果進行對比，如圖7所示。可以看出，不論是主震還是余震，實測強震記錄均值都在模擬均值加減一倍標準差的范圍內，這表明本文的模擬方法可以準確地反映主余震特征，具有良好的工程適用性。

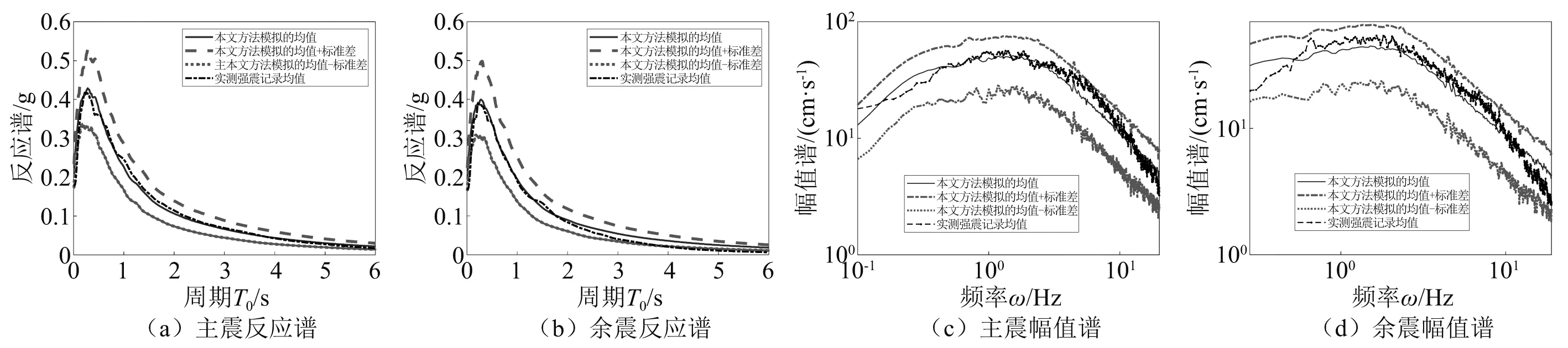
圖7 模擬的主余震地震動加速度的反應譜和傅里葉幅值譜與實測記錄的比較

6 結 論

本文在非平穩地震動的演變功率譜密度模型的基礎上，建議了該模型參數的識別方法，并利用實測主余震地震記錄識別了模型參數。基于Copula理論，實現了主余震參數之間的相關性分析。結合譜表示-隨機函數方法，建立了主余震型地震動的降維模型，生成了主余震型地震動的代表性時程。文中實現了從主余震實測記錄出發、獲取參數的邊緣分布、到生成具有考慮參數相關性的主余震型地震動過程的代表性時程，再到與實測主余震型地震動記錄的頻譜特性進行對比的全過程，得出以下結論：

(1)主震的峰值加速度比余震有偏大的趨勢；余震與主震相比，場地土卓越圓頻率較大，阻尼比較小，時頻調制函數參數a較大，這代表著余震能量比主震更小，衰減速度比主震更快。

(2)主余震參數之間大多保持著一定的相關性，其中峰值加速度PGA、場地土卓越圓頻率和調制函數參數a之間保持著中等的相關性，而阻尼比之間表現為低相關性。不同場地的場地土卓越圓頻率和阻尼比之間均保持著中等負相關性。此外，在不同主震參數取值的條件下，余震對應參數的概率密度函數有顯著的區別。

(3)主余震型地震動過程的降維模擬方法僅需數百條樣本即可在全概率信息上反應主余震地震動過程的概率特性，這為應用概率密度演化理論進行主余震型地震動作用下工程結構的隨機動力反應分析與可靠度評估奠定基礎。