基于頻變阻尼特性的四參數隔振系統建模與參數分析
蒲華燕,何文元,孫 翊,丁基恒,羅 均,謝少榮,彭 艷,王 敏
(上海大學 機電工程與自動化學院,上海 200444)
傳統被動隔振器通常是由彈簧和黏性阻尼器并聯組成的兩參數隔振系統。由于其具有控制簡單、穩定性好,且不需要外部電源等優點,廣泛用于航天工程[1-6]等領域。但近年來,隨著軌道衛星、遙感衛星搭載的任務載荷精度不斷提升,其對振動環境的要求也不斷提高。加之,軌道衛星、遙感衛星等在軌運行時存在極強的微振動、微重力環境,其具有振幅小、頻帶寬等特點,多為頻率范圍在0.1~300 Hz的諧波干擾[7-8]。因此,對高精度有效載荷免受微振動影響提出了更高的性能挑戰[9-18]。
傳統兩參數被動隔振系統通過阻尼調節消耗微振動能量實現隔振。當阻尼較大時,共振峰處的振動得到有效抑制,但是高頻段隔振性能變差,無法有效保證太空載荷高頻振動衰減的快速性;當阻尼較小時,高頻段隔振性能較好,但是共振峰不能得到有效抑制,從而誘發太空載荷低頻共振,甚至對載荷設備造成破壞。因此,對于航天器中的特殊微重力、微振動環境,兩參數被動系統在共振頻率和高頻的隔振性能存在固有的相互矛盾,無法有效滿足實際使用需求。
為了解決兩參數被動系統的相互矛盾,需要一種同時具有低頻大阻尼、高頻小阻尼的隔振系統,即系統阻尼會隨著頻率的增大而減小,從而實現低共振峰值和良好的高頻隔振性能,具備此特性的系統定義為頻變阻尼系統。頻變阻尼系統由于能夠同時保證共振區和高頻段的隔振性能,具有廣泛的研究前景。
因此,在兩參數被動系統的基礎上,為了探索頻變阻尼特性,三參數被動系統的隔振器被設計和研究。三參數系統由彈簧和彈性支撐的阻尼器并聯組成,可以通過合理調節參數值調諧系統,使其隔振性能優于兩參數系統。曾有學者對基于三參數的被動隔振系統進行了嘗試,初次嘗試結果表明,三參數系統在防沖擊方面表現出明顯的優勢。但是,隨著主動反饋控制算法的提出[19-20],有效的從源頭上克服了兩參數被動系統在低頻隔振性能與高頻衰減性能之間的矛盾,三參數被動系統的研究停滯了很長時間。
隨著航天技術的快速發展,航天器中的任務載荷對隔振器的可靠性、穩定性要求越來越高,由于主動隔振技術需要輸入外部能量且控制結構復雜、不穩定,這兩點很大程度上限制了其在航天領域的應用。于是,很多學者重新開始研究三參數被動系統。例如,Liu等[21]開發了一種基于三參數系統的流體黏性阻尼器,性能優于傳統被動隔振器。Brennan等[22]研究了三參數系統在自由振動和強制振動下的動力學行為,確定和比較了系統在不同類型的激勵下的最佳阻尼值,作者指出,對于簡諧激勵來說,系統具有較好的隔振效果;當系統被白噪聲激勵時,附加彈簧沒有表現出明顯的優勢。王超新等[23]給出了一種三參數隔振系統在最優阻尼下的設計方法。焦小磊等[24]提出了基于歸一化模型的三參數隔振系統優化設計方法,對共振峰和高頻衰減率進行了多目標優化設計。Zhang等[25-26]研究了基于三參數系統的隔振平臺的性能,提出了基于頻域特征的隔振平臺參數設計方法和流程。王杰等[27-28]提出一種確定三參數模型阻尼系數的機械阻抗等效理論與測試方法,將三參數模型簡化為等效的便于試驗測試的兩參數隔振模型,得到了以往傳統方法難以得到的動態阻尼系數隨頻率的變化規律。Silva等[29]研究了三參數模型中用非線性立方彈簧代替主彈簧的影響,結果表明,當立方剛度屬于軟化類型時,可以改善隔振器在共振頻率附近和高頻的傳遞率。Wang等[30]指出了三參數模型中非線性次級彈簧的使用能夠較好地改善系統高頻和共振頻率處的隔振性能。以上研究主要側重于三參數系統隔振性能的優化設計和分析,而很少考慮阻尼器和次彈簧之間實際存在的等效質量對系統性能帶來的影響。
因此,提出了一種基于頻變阻尼特性的四參數隔振系統,并對其進行系統建模與參數分析。提出的四參數隔振系統是一種基于三參數系統的等效模型,在阻尼器和次彈簧之間附加一個中間等效質量,從而疊加形成四參數系統。通過歸一化參數,建立四參數系統的理論模型,分析各參數對系統隔振性能的影響,提出一種基于四參數系統參數優化的思路,并從頻域和時域上分析了系統的隔振性能,在掃頻信號激勵下,通過MATLAB/Simulink模擬仿真,驗證了系統理論計算模型的準確性。
1 四參數系統模型
1.1 模型描述
本文研究的四參數系統為單自由度系統,系統等效模型是基于兩參數系統模型和三參數系統模型,如圖1(a)和圖1(b)所示。

圖1 等效模型
四參數系統中負載質量m由主彈簧k和黏性阻尼器c并聯組合支撐,阻尼器c、中間等效質量m1和次彈簧k1依次串聯組合,如圖1(c)所示。
1.2 模型建立
根據牛頓運動定律,可以得到四參數系統的運動方程組
(1)
(2)
式中:x0為基礎位移;x1,x分別為中間等效質量和負載質量的位移。
對參數進行歸一化處理,令N=k1/k,P=m1/m,其中:N為剛度比;P為質量比,且均為正實數。對式(1)變換,得到中間等效質量的位移
(3)
對式(3)在時間上求導兩次,可得到
(4)
(5)
綜合式(2)~式(5),得到四參數系統的四階常微分方程
(6)
(7)
對式(7)兩邊同時進行拉普拉斯變換,可以得到
(8)
根據傳遞率定義,將系統輸出信號X(s)與輸入信號X0(s)取比值,即可得到系統傳遞率
(9)
對式(9)進行傅里葉變換,將s=jω(其中j2=-1)代入式(9)中,則系統的傳遞率可表示為
(10)
式中,Ω=ω/ω0為頻率比,ω為外部激勵頻率。傳遞率的幅值可定義為
(11)
另外,四參數系統的傳遞率模型可等效為
(12)
綜合式(9)和式(12),可得到四參數系統的等效阻尼
(13)
2 參數N,P和ζ0對系統性能的影響
根據以前的經驗,初取ζ0=0.4,ω0=2π×7。首先,利用MATLAB軟件分析N和P對系統頻域性能的影響,得到N和P的較優取值范圍;然后,保持N和P的優化取值不變,分析阻尼比ζ0對系統傳遞率特性的影響。性能指標為共振峰值大小和高頻衰減率。通過優化參數,使四參數系統具有近似理想頻變阻尼系統的特性,如圖2所示。
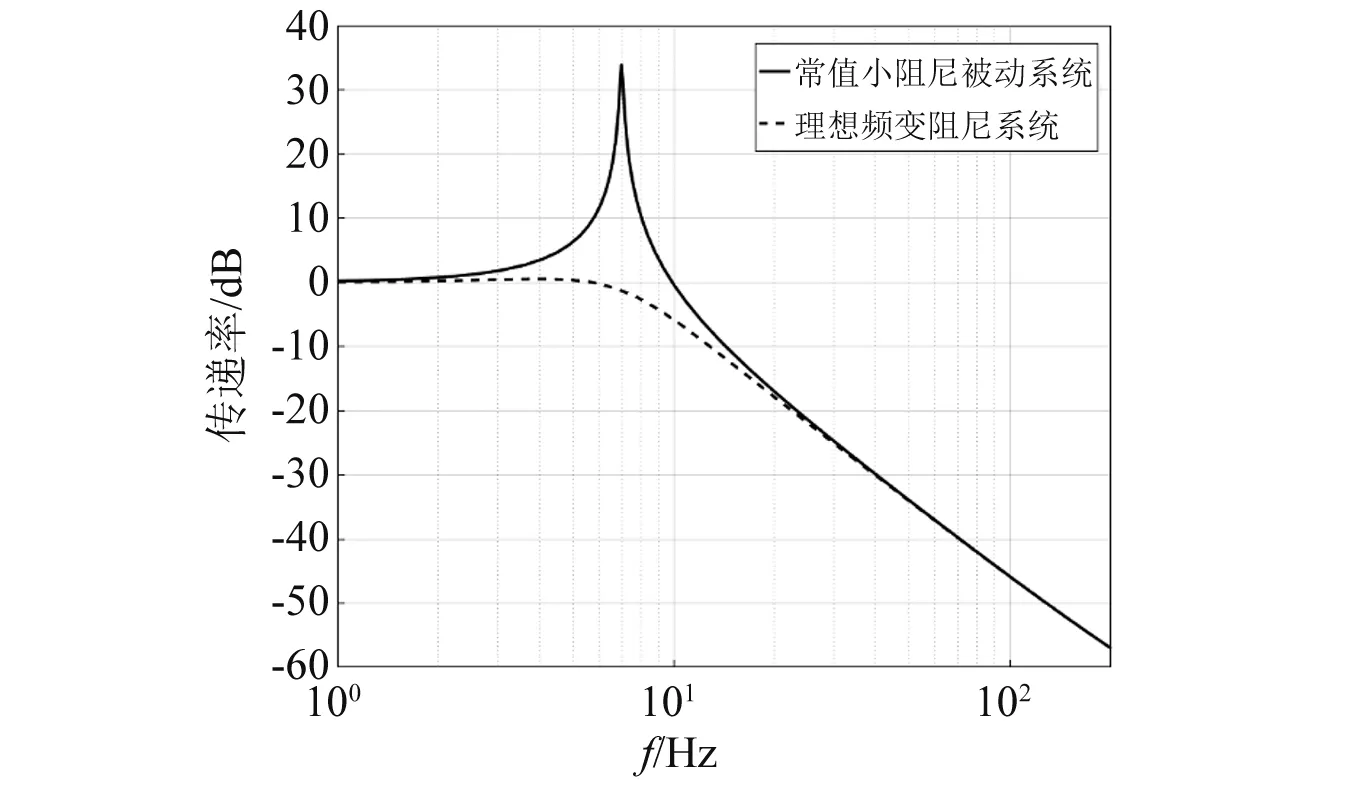
圖2 頻變阻尼特性曲線
2.1 情況1:P不變,N增大
保持P不變,分析N對系統性能的影響。其中P分兩種情況考慮:0
P分別等于0.5,2.0和5.0,N從0.1增大到5.0時系統的頻域響應,如圖3所示。從圖3可知,當N增大時,系統共振峰值降低,同時系統固有頻率右移。
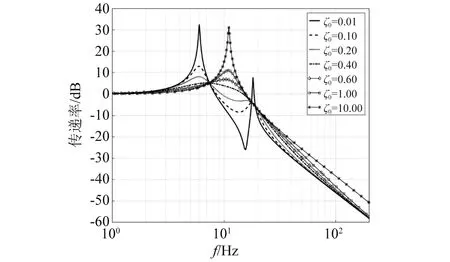
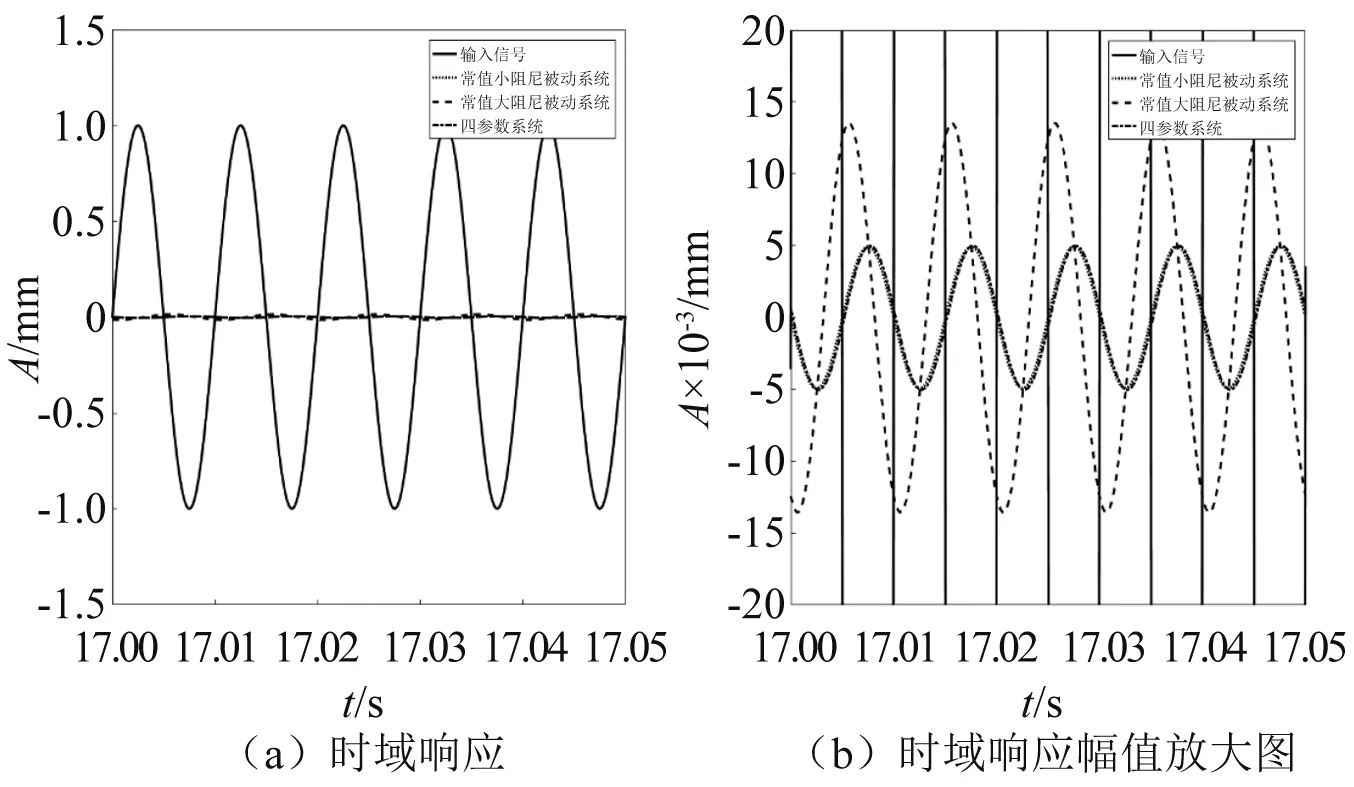
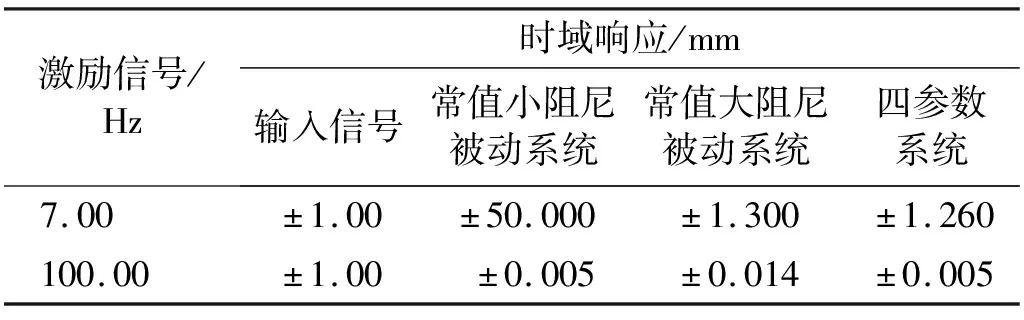
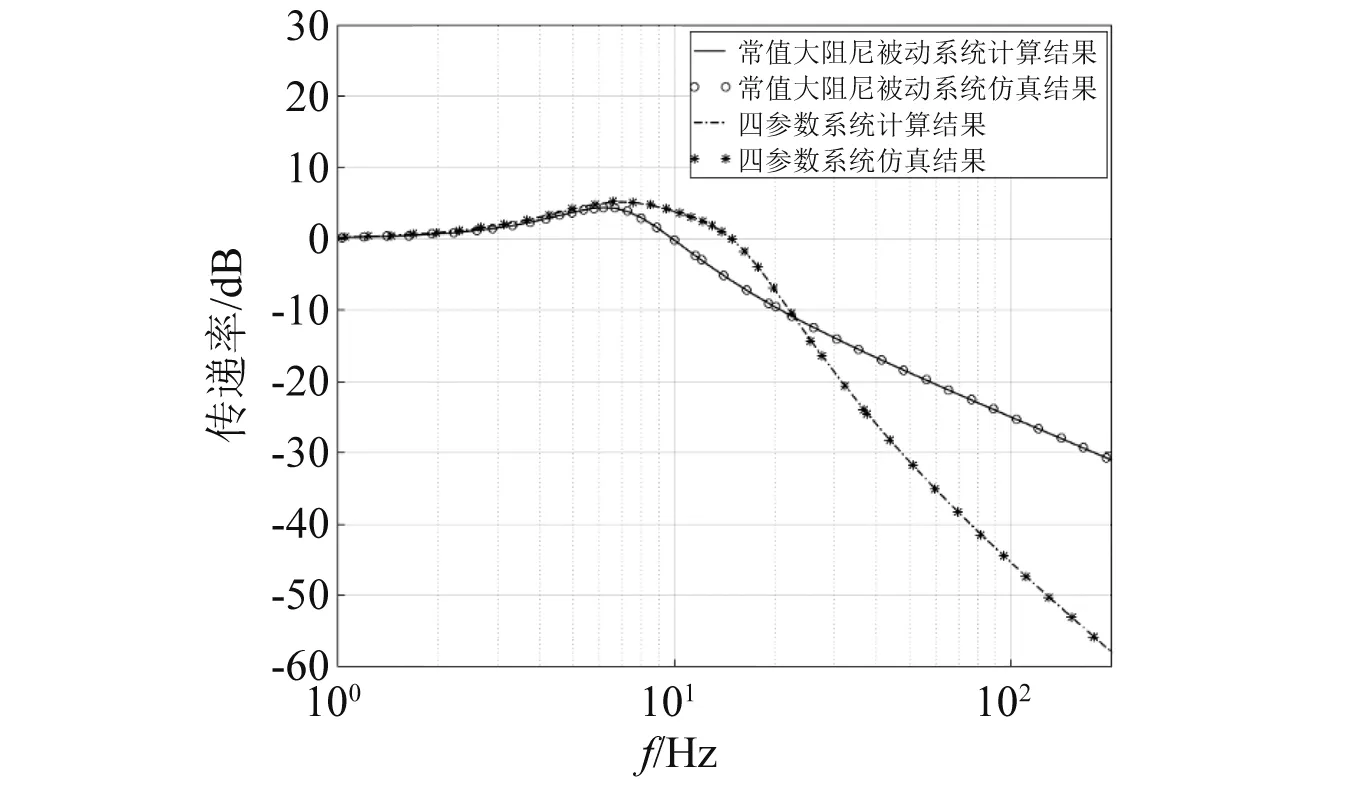
對比圖3(a)、圖3(b)和圖3(c),當P增大時,相同N值下系統傳遞率幅值會隨之增大,并在低頻出現新的峰,這是由中間等效質量m1增大引起的。當P在0 當N的取值范圍約為1.0 圖3 質量比常值時的頻率響應 分析N=1.5時,P(其中0 圖4 剛度比常值時的頻率響應 圖4(a)為N= 1.5,P從0.1增大到0.9時系統的頻域響應。從圖4(a)可知,共振峰值隨P的增大而降低,系統高頻衰減率隨P增大而增大。但是在共振頻率往右的某一頻率點后,當P>0.3時出現一個新的峰,并且峰值隨著P的增大而增大; 由圖4(a)可知,為了使系統具有近似理想頻變阻尼的特性,P的取值范圍可縮小為0.1 當P=0.2時,6~11 Hz頻段的峰值較高;當P=0.4時,11~20 Hz頻段的峰值較高。因此,綜合以上兩種情況,為了使系統在整個頻段內(6~20 Hz)的傳遞率幅值較低,選擇參數P=0.3。 當P=0.3時,對N在1.0 由2.1節和2.2節可知,剛度比N主要影響系統共振處的性能,質量比P主要影響系統高頻衰減性能。 系統在不同阻尼比ζ0下的傳遞率特性,如圖5所示。從圖5可知,系統共振峰值最初隨著ζ0的增大而減小,然后又增大,但共振峰出現在更高的頻率處。當阻尼比ζ0趨于零時,系統傳遞率曲線出現兩個峰,并且峰值逐漸增大。出現雙峰是由于四參數系統屬于四階系統,當參數取值通過臨界值時,系統頻域響應表現出雙共振峰現象。雙峰的幅值大小受系統阻尼c變化的影響,當系統阻尼c變小時,雙峰的幅值增大,此時四參數系統可等效為兩個二階系統的疊加,其中負載質量m和主彈簧k組成主要二階系統,中間等效質量m1和次彈簧k1組成次要二階系統,次要二階系統相當于一個吸振器。 圖5 不同阻尼比ζ0下的系統傳遞率特性 根據圖5可得,當N=1.5,P=0.3,阻尼比ζ0在0.4附近取值時,系統可同時實現低共振峰值和良好的高頻隔振性能,此時系統處于欠阻尼狀態。 經過第2章的討論和分析,得到了N,P和ζ0的較優取值范圍。本節從頻域和時域上對四參數系統進行性能分析。 兩參數被動系統的傳遞率為 (14) 取N=1.5,P=0.3,ζ0=0.4,ω0=2πf(f=7 Hz),利用MATLAB軟件可得到不同系統的頻域響應,如圖6所示。 圖6 不同系統的頻域響應 從圖6可知,四參數系統能夠較好地解決被動系統的矛盾,并且同時保持低共振峰值和良好的高頻衰減率。由于四參數系統存在次彈簧k1,系統總剛度大于被動系統,因此,四參數系統的固有頻率發生了右移。 將各系統的頻域響應數據根據圖6列于表1中。其中,7.00 Hz為被動系統的固有頻率,22.80 Hz,125.36 Hz,126.46 Hz分別為四參數系統與常值大阻尼被動系統、常值小阻尼被動系統、理想頻變阻尼系統的相交頻率。 表1 不同系統的頻域響應 相較于常值小阻尼被動系統的共振峰幅值34.00 dB,常值大阻尼被動系統能夠明顯降低共振峰幅值至4.04 dB,衰減了29.96 dB,但高頻的隔振性能卻損失了,具體如:22.80 Hz處由-19.64 dB上升至-11.04 dB,性能下降了8.60 dB;125.36 Hz處由-49.57 dB上升至-26.96 dB,性能下降了22.61 dB;126.46 Hz處由-49.71 dB上升至-27.04 dB,性能下降了22.67 dB。 相較于常值小阻尼被動系統的共振峰幅值34.00 dB,四參數系統能夠明顯降低共振峰幅值至5.15 dB,衰減了28.85 dB,同時高頻的隔振性能隨頻率增大而變好,具體如:22.80 Hz處由-19.64 dB上升至-11.04 dB,性能下降了8.60 dB;125.36 Hz處兩個系統均為-49.57 dB,性能一致;126.46 Hz處由-49.71 dB下降至-49.73 dB,性能上升了0.02 dB。 相較于常值大阻尼被動系統的共振峰幅值4.04 dB,四參數系統的共振峰幅值僅上升了1.11 dB,但是高頻的隔振性能得到較大提升,具體如:22.80 Hz處兩系統均為-11.04 dB,性能一致;125.36 Hz處由-26.96 dB下降至-49.57 dB,性能上升了22.61 dB;126.46 Hz處由-27.04 dB下降至-49.73 dB,性能上升了22.69 dB。 綜上,相較于常值小阻尼被動系統,四參數系統共振峰幅值降低28.85 dB,比常值大阻尼被動系統共振峰幅值僅低約3.70%;相較于常值大阻尼被動系統,四參數系統在126.46 Hz的高頻隔振性能提升了22.69 dB,比常值小阻尼被動系統高頻處的性能高約0.09%。同時,以理想頻變阻尼系統頻域響應作為參考,當頻率從7.00 Hz增大至126.46 Hz時,兩個系統傳遞率幅值差值從6.48 dB先增大后減小至0,表明四參數系統隔振性能隨頻率增大而逐漸接近于理想頻變阻尼系統特性。因此,四參數系統能夠較好地解決被動系統高低頻隔振性能之間的固有矛盾,具有低頻大阻尼、高頻小阻尼的頻變阻尼特性。 正弦信號激勵時域響應如圖7所示。圖7(a)為在共振頻率處,7.00 Hz正弦信號激勵下的時域響應;圖7(b)為共振頻率處時域響應的放大圖。從圖7可知,當輸入信號幅值為±1.00 mm時,四參數系統和常值大阻尼被動系統的時域響應基本一致,幅值在±1.00~±1.50 mm,常值小阻尼被動系統的時域幅值在±40.00~±60.00 mm,表明四參數系統和常值大阻尼被動系統在共振頻率處具有相似的振動抑制效果,即低頻大阻尼特性,與圖6中共振頻率處各系統的傳遞率特性相對應。 圖7 7 Hz正弦信號激勵時域響應 100 Hz正弦信號激勵時域響應如圖8所示。圖8(a)為在高頻處,100 Hz正弦信號激勵下的時域響應;圖8(b)為高頻處時域響應的放大圖。從圖8可知,當輸入信號幅值為±1.00 mm時,四參數系統和常值小阻尼被動系統的時域幅值為±0.005 mm,常值大阻尼被動系統的時域幅值在±0.010~±0.015 mm。四參數系統和常值小阻尼被動系統在高頻處具有相似的振動抑制效果,即高頻小阻尼特性,與圖6中高頻處各系統的傳遞率特性相對應。 圖8 100 Hz正弦信號激勵時域響應 將各系統的時域響應數據根據圖7和圖8列于表2中。當激勵頻率為7.00 Hz時,相比于輸入信號±1.00 mm,常值小阻尼被動系統、常值大阻尼被動系統和四參數系統的時域幅值分別放大了50倍、1.30倍和1.26倍;相對于常值小阻尼被動系統,四參數系統和常值大阻尼系統在共振頻率處具有大阻尼效果。當激勵頻率為100.00 Hz時,相比于輸入信號±1.00 mm,常值小阻尼被動系統、常值大阻尼被動系統和四參數系統的時域幅值分別縮小了200倍、71.43倍和200倍;相對于常值大阻尼被動系統,四參數系統和常值小阻尼系統在高頻處具有小阻尼效果。因此,四參數系統能同時保證共振頻率和高頻處的低時域響應,具有低頻大阻尼、高頻小阻尼的特性。 表2 不同系統的時域響應 為了驗證四參數系統理論計算模型的準確性,根據運動方程式(1)和式(2),在MATLAB/Simulink中搭建仿真環境如圖9所示。仿真參數設置如表3所示。采用掃頻信號進行信號激勵,使用頻譜分析儀觀察系統輸出位移信號及傳遞率特性。理論計算結果與仿真結果的對比如圖10所示。 圖9 Simulink仿真 表3 仿真參數設置 圖10 理論計算與仿真對比 由圖10可知,當頻率為7.00 Hz時,常值大阻尼被動系統和四參數系統的計算結果分別為4.04 dB和5.15 dB,仿真結果分別為4.05 dB和5.16 dB,誤差分別為0.01 dB和0.01 dB;當頻率為100.00 Hz時,常值大阻尼被動系統和四參數系統的計算結果分別為-24.97 dB和-45.34 dB,仿真結果分別為-24.94 dB和-45.43 dB,誤差分別為0.03 dB和-0.09 dB。因此,四參數系統的仿真結果與理論計算結果基本吻合一致,驗證了理論計算模型的準確性,表明了四參數系統具有頻變阻尼特性。 (1)定義了頻變阻尼特性,即低頻大阻尼、高頻小阻尼的系統特性;通過歸一化參數,建立了四參數隔振系統的傳遞率模型,得到了系統等效阻尼,將系統物理參數轉換為無量綱參數,更易于分析四參數系統的性能。 (2)提出了一種基于四參數系統參數優化的思路,通過給定不同的初始條件ζ0和ω0,可以得到對應參數N和P的較優取值范圍。N和P的取值并非越大越好,均存在臨界點,臨界點之下越大系統性能越好,臨界點之上繼續增大會使系統性能變差。基于這個思路,為設計不同指標要求的微振動隔振器以及多參數隔振系統的參數優化提供基礎。 (3)從頻域和時域上對四參數系統進行性能分析;結果表明,四參數系統能夠較好地解決被動系統高低頻隔振性能之間的矛盾。利用MATLAB/Simulink對理論計算模型進行了模擬仿真驗證,仿真結果與理論計算基本一致。相較于被動隔振系統,四參數系統能夠將7 Hz固有頻率處的傳遞率幅值降低28.85 dB,證明低頻大阻尼效果顯著;同時,采用100 Hz單頻正弦信號激勵時,時域幅值從±1.00 mm衰減至±0.005 mm,衰減率達99.5%,證明高頻小阻尼作用凸顯,從而驗證了四參數系統的頻變阻尼特性,即低共振峰值和良好的高頻隔振性能。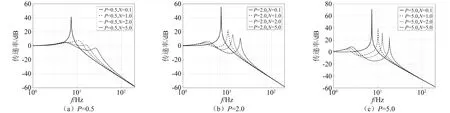
2.2 情況2:N不變,P增大

2.3 情況3:N=1.5,P=0.3時,ζ0增大
3 性能分析和模型驗證
3.1 頻域和時域性能仿真分析



3.2 模型驗證


4 結 論

