基于一致圖學習的魯棒多視圖子空間聚類

潘振君，梁 成，張化祥

（山東師范大學信息科學與工程學院，濟南 250358）

（?通信作者電子郵箱ALCS417@sdnu.edu.cn）

0 引言

聚類是機器學習中最熱門的討論話題之一，廣泛應用于數據挖掘、機器學習等多個領域。隨著數據分析技術的日益成熟，多視圖聚類成為人們關注的焦點。由于數據的異構性，傳統的單視圖聚類算法難以適用于某些特定場景。多媒體數據來源廣泛且表示形式多樣，例如，在一個新聞事件的報道中，報道的內容可能來自多個不同的新聞媒體機構，對該新聞的報道可能采用文字、圖片或視頻等形式［1-4］。不同的信息獲取方式和表示方式構成了多視圖數據。多視圖數據學習已經成為數據挖掘、多媒體計算等領域中尤為重要的一部分，越來越多的聚類算法被提出。在此之前，處理多視圖數據的方式是直接將多個視圖的特征進行拼接來構造一個新的特征矩陣，再對其應用單視圖聚類算法得到聚類的結果；但是這種方法有明顯的缺陷，它沒有考慮每個視圖之間的內部聯系，聚類性能也難以提高。因此學者們提出了多視圖聚類算法（Multi-View Clustering，MVC）。多視圖數據利用不同的視圖來描述事物的不同特征，但本質上是對同一事物的描述。與單視圖聚類算法相比，多視圖聚類算法彌補了單視圖聚類算法使用單一數據類型，不能考慮數據的多樣性和不同視圖之間的一致性等缺點。不同的視圖不僅包含了所有視圖共享的數據信息，還包含了彼此不同的特定信息，這就是多視圖數據的多樣性。對數據中的異構特征進行良好的融合，可以有效提高算法的魯棒性。

近年來，學者們提出了很多先進的多視圖聚類算法，根據處理和使用多視圖數據方式的不同，這些算法可以大致分為以下幾類：多視圖協同訓練算法、多視圖多核學習算法、多視圖圖學習聚類算法、多視圖子空間聚類算法。協同訓練最初是為解決半監督學習問題而提出的。在半監督學習中，數據由有標簽數據和無標簽數據組成，算法考慮利用多視圖數據和無標簽數據的信息來輔助傳統的監督學習，協同訓練算法的核心思想是利用多視圖數據和無標簽數據的信息來輔助傳統的監督學習，在多視圖數據上利用有標簽數據分別訓練多個分類器。在訓練過程中，每個分類器對無標簽數據中置信度較高的數據進行標記，并將標記后的數據加入到分類器的有標簽數據中，利用新標記不斷進行更新。最具代表性的算法為Blum 等［5］提出的協同訓練算法。文獻［6］中提出了一種結合K-means 聚類和線性判別分析的協同訓練算法，該算法利用一個視圖中的無監督聚類結果來學習另一個視圖中的判別子空間。多核學習（Multiple Kernel Learning，MKL）［7］算法是一類比單個核函數更具靈活性的基于內核的學習算法，多核學習的內核對應不同的視圖，因此多核學習在處理多視圖數據方面得到了廣泛的應用。在多核框架下，樣本在特征空間中的表示問題轉化為核與權系數的選擇問題。多核學習中的一個關鍵步驟是根據每個內核的重要性為其分配一個合理的權重。文獻［8］中提出了一種改進的算法，該算法通過學習低秩核矩陣來獲得相似度，并在核的鄰域內找到最優核。文獻［9］中提出了聚類加權核K均值算法，為不同視圖的內部簇分配權重，并應用核K均值，學習不同視圖共同的聚類指標矩陣。由于圖是表示各種類型對象之間關系的重要數據結構，因此基于圖學習的聚類方法也被廣泛地用于聚類任務。圖中的每個節點對應一個對象，每條邊表示兩個對象之間的關系，用權重衡量相鄰樣本點之間的相似度。

權值越大相似度越高，被劃分到同一類的概率越大。文獻［10］中提出了一種基于三階段圖的多視圖聚類算法，該算法結合子空間的圖表示和層次聚類方法，但未考慮不同視圖的權重；文獻［11］中則進行了基于加權多視圖的聚類研究。這兩種算法首先為每個視圖生成一個相似度圖，然后對每個圖進行加權來構建統一表示，從而生成最終的聚類結果。

本文主要研究多視圖子空間聚類算法。子空間分割聚類算法是近年來學者廣泛研究的重點，涉及機器學習、計算機視覺和模式識別等多個領域。子空間聚類算法是將原始數據集映射到其子空間表示，然后構造低秩的相似矩陣。該方法保留了原始數據集的相關性，能更好地揭示數據的子空間結構。近年來，基于子空間的多視圖聚類算法由于其有效性而得到發展［12-15］。這些算法旨在發現嵌入在原始數據中的底層子空間，從而得到更加準確的聚類結果。為了有效地整合來自不同視圖的特征，設計了各種多視圖子空間聚類算法，并取得了顯著的效果。這些算法的主要區別在于對表示系數矩陣進行正則化。如文獻［16］中的稀疏子空間聚類（Sparse Subspace Clustering，SSC）算法對數據表示使用?0范數正則化；但問題是非凸的，不能直接求解，因此作者使用相應的凸代替?1范數獲得問題的最優解。文獻［17］中提出的魯棒低秩表示分割算法通過最小化數據表示的秩得到一個低秩表示矩陣，并采用交替方向最小化的增廣拉格朗日乘子方法（Augmented Lagrange Multiplier Method with Alternate Direction Minimization，ALM-ADM）求得最優解。

現有的多視圖聚類算法已經取得了許多優異的成果，但目前多視圖下的聚類任務仍存在一些亟待解決的問題：

1）原始數據集中通常存在誤差、離群值等噪聲的干擾，直接在原始數據集上學習相似度矩陣，會對聚類結果產生影響；

2）一些算法中沒有考慮不同視圖之間差異，不同的視圖對聚類結果有不同的重要性，一般通過引入參數來解決這個問題，但這會使算法更加復雜；

3）許多方法需要引入額外的聚類步驟才能得到最終的聚類結果。

為了解決上述問題，本文提出一種基于一致圖學習的魯棒多視圖子空間聚類（Robust Multi-view subspace clustering based on Consistency Graph Learning，RMCGL）算法。該算法首先學習原始數據在低秩子空間的潛在魯棒表示，然后根據該表示學習不同視圖下的相似度矩陣。考慮到不同視圖之間的多樣性，根據相似度矩陣聯合學習一個一致圖，并通過自適應的方式自動調整不同視圖的權重。為了有效求解目標函數，算法采用交替方向極小化的拉格朗日乘子優化算法。與傳統的多視圖子空間聚類算法相比，RMCGL 算法在仿真數據集及真實數據集上均表現出較好的性能。圖1 給出了RMCGL算法的流程。

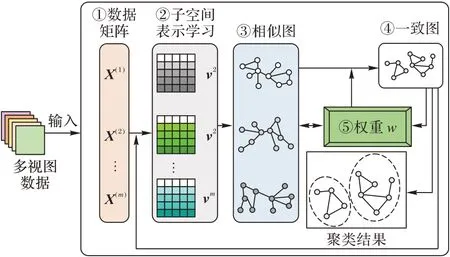
圖1 RMCGL算法流程Fig.1 Flowchart of RMCGL algorithm

1 相關工作

本章將簡要介紹與本文密切相關的兩個已有研究工作：基于低秩表示（Low-Rank Representation，LRR）的魯棒子空間分割［18］和基于多視圖聚類與自適應鄰居（Multi-view Learning with Adaptive Neighbours，MLAN）的半監督分類［29］。其中，LRR是單視圖聚類算法，MLAN為多視圖聚類的算法。

1.1 LRR

LRR 是一種基于低秩表示的聚類算法，該算法與SSC 非常相似，但其目標是在所有候選向量中尋找一種低秩表示而非稀疏表示。給定一組向量X=[x1，x2，…，xn]，假設這些向量來自k個獨立子空間的并集，算法的目標是在d維歐氏空間中，將所有數據向量分割到它們各自所屬的子空間中。因此，LRR算法通過求解下面的凸優化問題找到D：

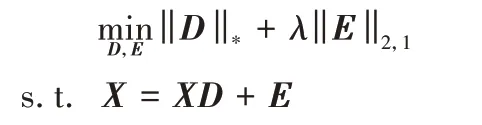
1.2 MLAN

MLAN 是一種基于自適應鄰居節點的多視圖聚類算法。該算法從數據點的角度將每個視圖的特征融合，求出一個統一的相似度圖U。MLAN 是對基于自適應鄰居聚類（Clustering with Adaptive Neighbors，CAN）［20］的擴展，可以同時進行多視圖聚類和局部流形結構學習。該算法如下所示：

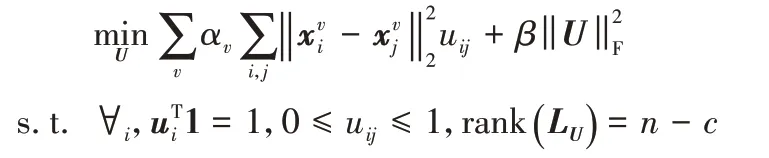
2 基于一致圖學習的魯棒多視圖子空間聚類

本章將詳細介紹本文所提出的RMCGL 算法以及其求解和優化過程。首先介紹一些基本符號的含義。矩陣和向量分別寫成加粗斜體大寫字母和加粗斜體小寫字母；Frobenius 范數的符號為‖ ? ‖F，?2范數的符號為‖ ? ‖2；其他本文常用的符號定義見表1。

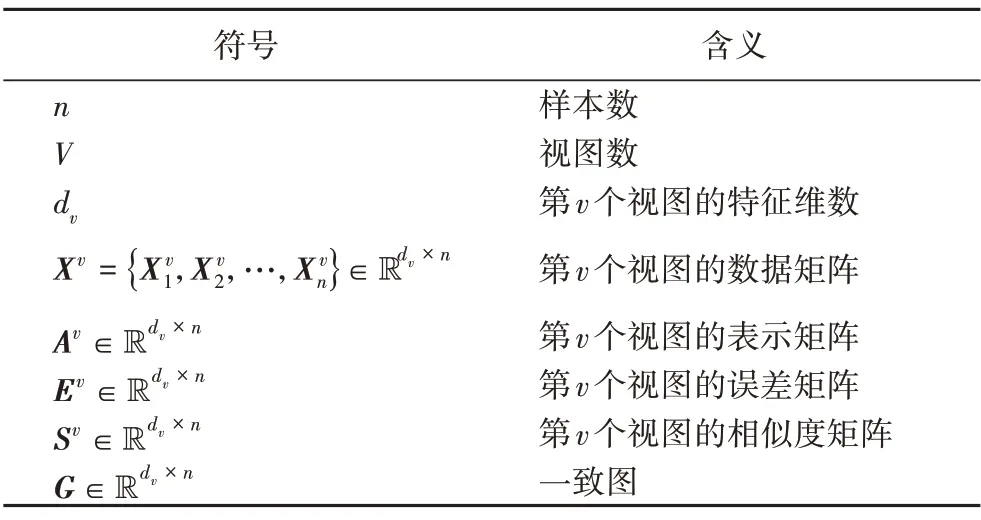
表1 常用符號及其定義Tab.1 Common symbols and their definitions

2.1 RMCGL算法

給定V個視圖X1，X2，…，XV為各個視圖對應的數據矩陣，其中第v個視圖表示為Xv={Xv1，Xv2，…，Xvn}∈Rdv×n。對于任一視圖Xv中的數據，其通常是存在于一個潛在的低維空間中而非均勻分布于整個空間，因此，所有的數據都可在低維子空間中進行表示。基于此，首先將LRR 算法擴展到多視圖學習中，即有：

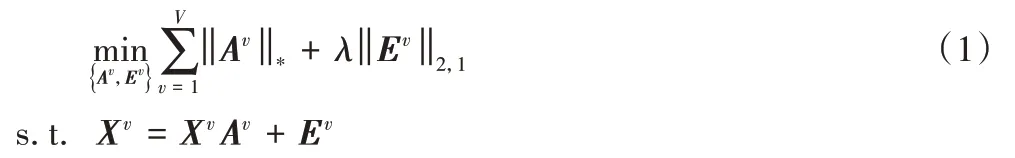
其中：Av和Ev的定義如表1 所示。通過式（1）可以獲得各視圖下數據的子空間表示矩陣，并且能夠有效消除原始數據中噪聲或異常值的影響。該過程對噪聲具有魯棒性，可得到不同視圖的潛在魯棒表示；但式（1）中沒有考慮不同視圖間的聯系，也無法直接獲得有效的相似度矩陣進行聚類。一個可行的解決方法是將Av作為各個視圖下的相似度矩陣，然后通過目標函數學習一個統一的相似度矩陣A。然而，盡管該方案可行，但Av作為相似度矩陣所代表的含義與其本質的定義并不相同。為了解決該問題，本文利用Av作為樣本的潛在特征表示，為各個視圖學習一個新的相似度矩陣Sv，目標函數如下：

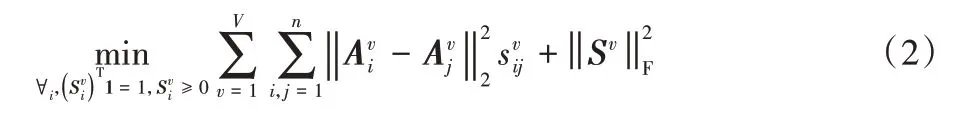
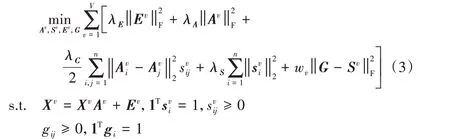
其中：λA、λS、λE是三個非負參數，用來平衡各項；wv={w1，w2，…，wv} 用來衡量不同視圖之間的權重。在LLR 算法中表示學習和誤差項分別采用核范數和?2，1范數，但是為了使后續優化問題方便求解，本文中表示學習和誤差項均采用F范數。公式中的前兩項用來學習每個視圖的潛在魯棒表示，即圖1 中①、②過程，不同于直接在原始數據上學習相似度矩陣，該過程考慮了原始數據噪聲的干擾。為了獲得更好的聚類結果，三、四兩項（圖1 過程③）根據得到的魯棒表示，學習不同視圖的相似度矩陣。最后一項的目的是利用多個相似度圖，學得一個一致圖，如圖1 過程④所示，該過程充分考慮了視圖間的多樣性。引入權值參數w（圖1 過程⑤）為不同視圖分配合適的權值。本文RMCGL算法采用自加權方式，其更新規則將在下一節中詳細介紹。此外，為了直接通過一致圖G得到最終的聚類結果而不借助于其他的聚類算法，本文對圖G的拉普拉斯矩陣施加一個秩約束rank(LG)=n -c，使得一致圖G中連通分量的個數恰好等于聚類的個數c，由此得到如下結果：

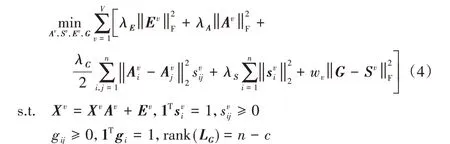
由于秩約束的存在導致上式求解困難，因此，采用秩約束的等價形式。令σc(LG)為LG第c小的特征值，LG是半正定的，有σc(LG)≥0。根據圖拉普拉斯矩陣的性質，特征值為0 的重數c等于圖G中連通分量的個數。即LG應有c個0 特征值，此時滿足秩約束條件。根據Ky Fan’s 定理［21］，有

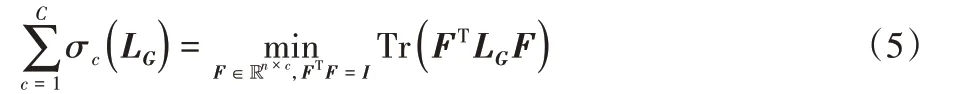
其中：F為標簽矩陣。因此，式（4）中的秩約束可由式（5）表示，將式（4）和（5）結合得到最終的目標函數如下所示：

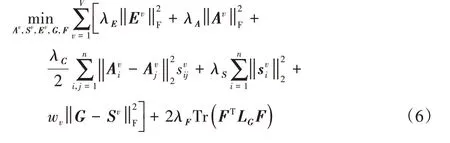
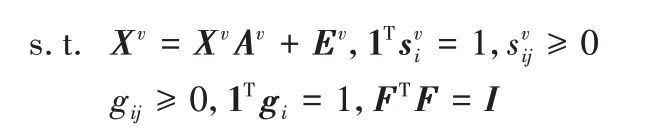
2.2 算法求解

本節對提出的RMCGL算法進行詳細的求解。由式（6）可以看出，該算法在一個統一的優化框架中學習與數據表示相關的親和圖。算法中有五個變量需要求解，考慮到式（6）同時關于所有的求解變量是非凸的，但當其中一個變量固定時，對其他變量的優化都是凸的，因此本文采用交替方向最小化（Alternating Direction Minimizing，ADM）策略［22］的增廣拉格朗日乘子（Augmented Lagrangian Multiplier，ALM）對目標函數進行求解。首先引入一個輔助變量C來代替目標函數第三項中的A，以分離變量。算法的增廣拉格朗日函數如下：

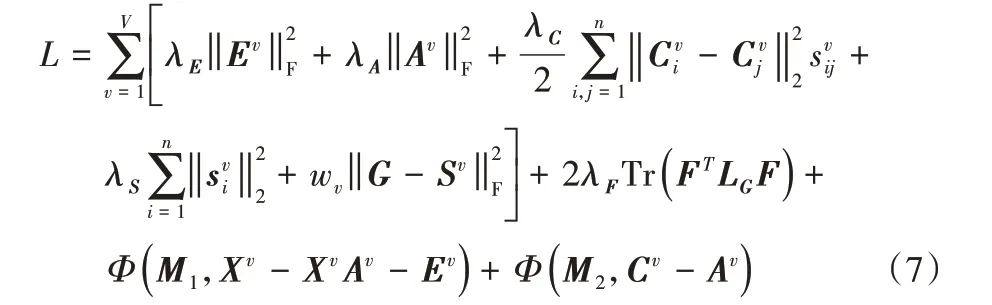
其中：M1和M2是拉格朗日乘子，定義，其中μ＞0是懲罰參數。

1）更新E。

當固定其他變量時，只保留增廣拉格朗日函數中包含E的項，對其求偏導后置0，可得如下結果：

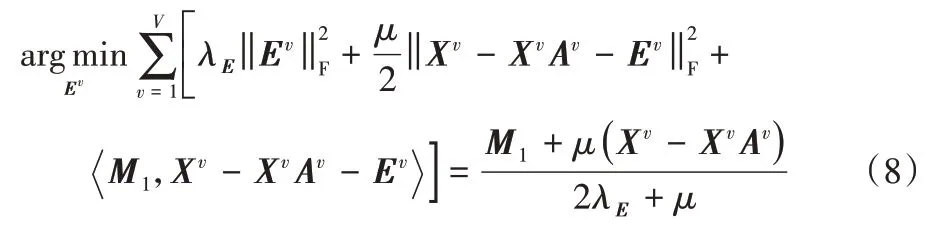
2）更新A。

只保留與A相關的項，然后對A求導并置0，得到如下結果：

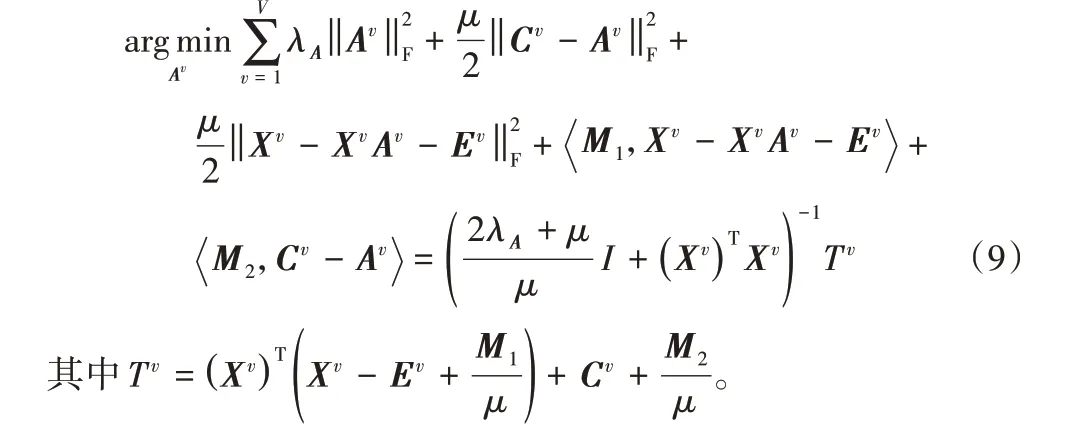
3）更新C。

與求E和A的方法類似，C的更新規則如下：

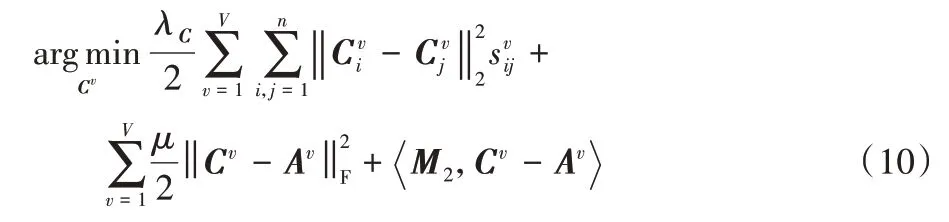
根據拉普拉斯矩陣的定義，很容易得到

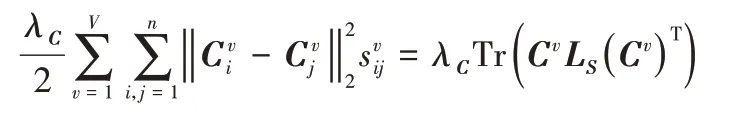
因此Cv的解如下：

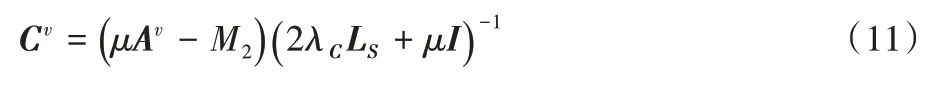
4）更新S。

對于S的求解，可以將其看作是在求解以下優化問題：

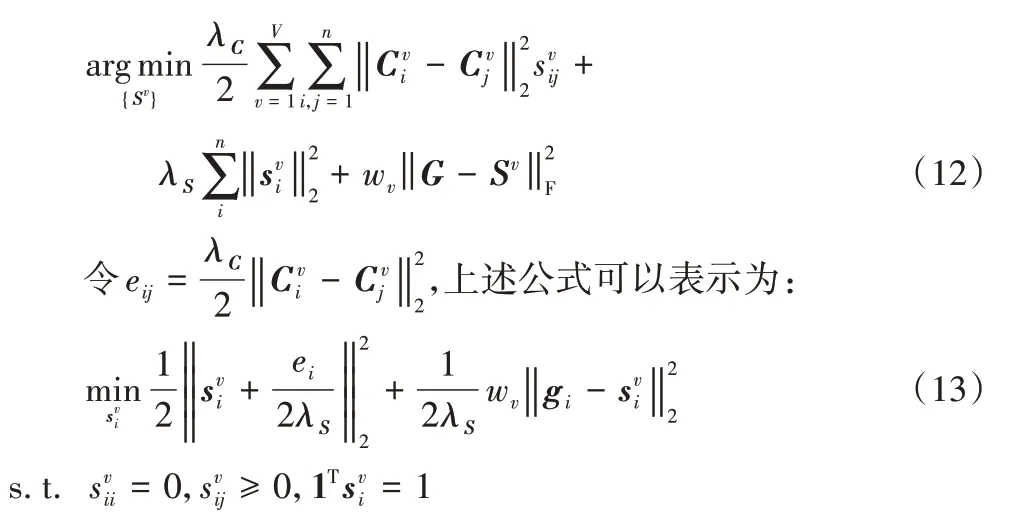
該問題可同樣根據約束條件利用拉格朗日函數進行求解，最終求得S的解如下：

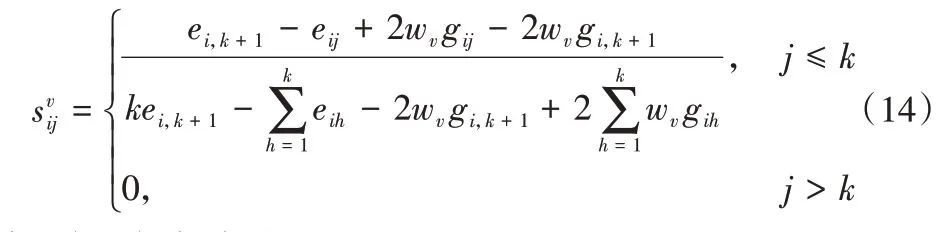
其中si有k個非零項。

5）更新G。

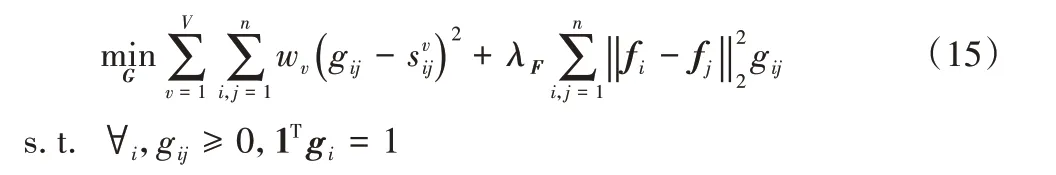
值得注意的是，問題（15）對于每個不同的i是獨立的，可單獨求解。因此可將式（15）進一步轉化為：

該步驟的詳細求解過程可參考文獻［23］。

6）更新F。

F可以通過最小化以下公式求得：

F的最優解由LG的c個最小特征值對應的c個特征向量構成。

7）更新權重wv。

8）更新拉格朗日乘子M1和M2。

除了上述變量的更新外，還有兩個拉格朗日乘子需要更新，更新規則如下：

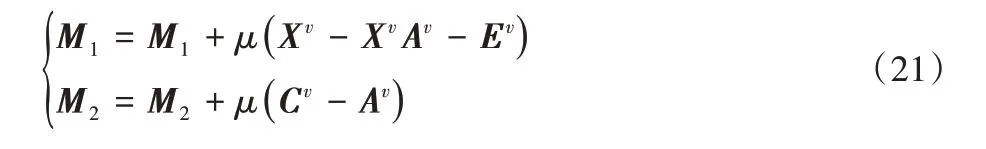
綜上所述，目標函數（6）的詳細求解過程如算法1。

算法1 RMCGL算法

2.3 時間復雜度分析

本文提出的RMCGL算法求解時采用的是迭代求解方式，可將算法分為多個子問題單獨計算，因此，該算法的時間復雜度可以通過計算每個子問題的時間復雜度獲得。每個子問題的時間復雜度如下：式（14）更新每個視圖的相似度矩陣Sv，其時間復雜度為O（Vnk）；此外對相似度矩陣初始化所用時間復雜度為O（Vnkd）；式（18）更新學習到的一致圖G，其時間復雜度為O（cn），其中c是聚類的個數；式（19）更新F，需要計算拉普拉斯矩陣的特征向量，其時間復雜度為O（cn2）；式（20）更新自加權系數w，其時間復雜度為O（Vn2）。假設該算法迭代次數 為t，則該算法的時間復雜度為O（t（Vnk+cn+cn2+Vn2）+Vnkd）。

3 實驗設計與結果分析

為了驗證RMCGL算法的有效性，利用三個常用評價指標在2 個仿真數據集、6 個真實數據集以及4 個癌癥數據集上與其他算法進行了比較。此外，還設計了多個實驗來進一步對所提出的算法進行分析，包括：收斂性實驗、參數分析實驗、消融實驗和魯棒性實驗。

3.1 數據集描述

3.1.1 仿真數據集

本文使用兩個合成的仿真數據集來衡量RMCGL 算法的聚類效果。

synthetic 數據集［24］涉及三個基因組數據集，分別為RNA表達、DNA 甲基化和miRNA 表達。首先，對三個基因組數據集進行數據預處理，分別隨機抽取200 個缺失率低于20%的樣本，采用k近鄰算法，將200 個完整樣本的非空鄰居的均值賦值給缺失部分，得到第一種類型的數據矩陣，對其進行奇異值分解得到。隨后構造三個由多個簇組成的數據矩陣Yi=Bi+θ，其中Bi從｛0，2，4，6｝中隨機抽樣得到，代表不同簇的偽生物表達水平，θ～N(0，1)為隨機偏差，由此得到第二種類型的數據矩陣。最后，將這兩種類型的數據矩陣進行重構，得到最終的仿真數據集。

two Gaussian 數據集［25］是一個隨機生成的高斯數據集，在這個數據集中有兩組服從高斯分布的數據，共200 個樣本。第一個視圖的均值為，協方差為。第二個視圖的均值為，協方差為。

3.1.2 真實數據集

6 個數據集分別為100leaves、BBC、NGs、Caltech101-20、COIL-20 和MSRC，詳細情況如下（總結見表2，其中v1～v6表示不同視圖的特征數）。

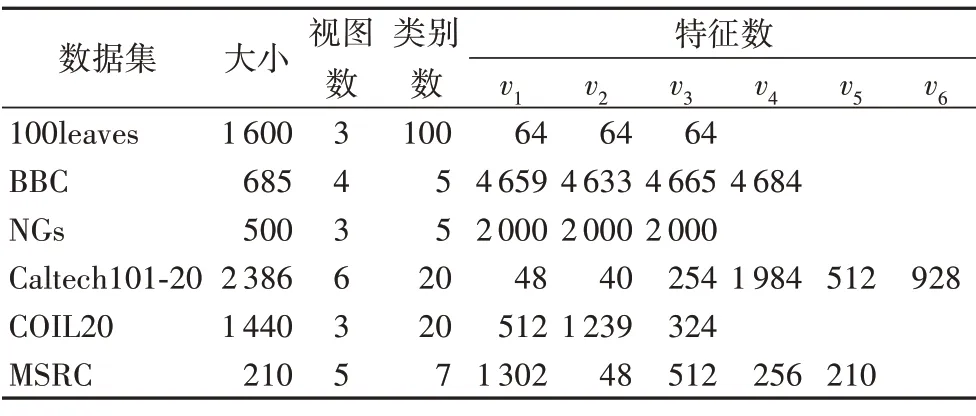
表2 六個真實數據集的詳細描述Tab.2 Detailed description of six real-world datasets

1）100leaves 數據集。該數據集由100 種植物的1 600 個樣本組成，每個樣本特征包含形狀描述、細尺度邊緣和紋理直方圖。

2）BBC 數據集。該數據集由BBC 新聞網站的685 份文檔組成，這些文檔對應五個領域，分別為商業、娛樂、政治、體育和科技。

3）新聞組數據集（NGs）。該數據集包含20個子集的新聞組數據集，由500 個新聞組文檔組成。每個原始文檔都用三種不同的方法進行預處理（有監督互信息預處理、無監督互信息預處理和分區預處理），構成三個視圖，并使用五種主題標簽中的一種進行注釋。每個新聞組對應一個不同的主題。

4）Caltech101-20 數據集。該數據集包含20 類2 386 幅圖像，每幅圖像都有6 個特征，分別為：Gabor 特征、小波矩（Wavelet moments）特征、統計轉換直方圖（CENsus Transform HISTogram，CENTRIST）特征、方向梯度直方圖（Histogram of Oriented Gradient，HOG）特征、通用搜索樹（Generalized Search Trees，GiST）特征和局部二值模式（Local Binary Pattern，LBP）特征。

5）COIL-20 數據集。該數據集包含20 個對象，將每個對象水平旋轉360°，每隔5°拍攝一張照片。每個對象有72張圖像，圖像像素大小為64×64，灰度圖像共計1 440張圖像。

6）MSRC 數據集。該數據集有5 個視圖，包含7 種類別（樹、建筑、飛機、牛、臉、汽車和自行車）的210張圖像。

3.1.3 癌癥數據集

機器學習算法在生物醫學領域應用廣泛，為了驗證該算法在癌癥亞型分類上的效果，從人類癌癥數據庫TCGA 中挑選了4個數據集，分別為Breast、Colon、GBM 和Melanoma，每個數據集包含三個組學數據：基因表達、DNA 甲基化和miRNA表達數據。

3.2 實驗方案

參數設置：目標函數中有四個參數λE、λA、λC、λF，λE、λA、λC的取值范圍為［0.01，0.1，1，10，100］。在聚類過程中對λF采用自動更新的方式，初值設為1，在每次迭代中，當一致圖G的連通分量分別小于或大于聚類的簇數時增大或減小λF(λF=λF*2，λF=λF/2)。最近鄰個數為15，對于每個方法和數據集，重復運行30次記錄平均結果。

為了評估該算法的性能，本文將該算法與現有的多種聚類算法進行了對比。典型的單視圖對比算法有：非負矩陣分解（Nonnegative Matrix Factorization，NMF）［26］和自適應鄰居節點聚類CAN。多視圖對比方法包括基于圖的多視圖聚類系統GBS（Braph-Based System）［27］、多視圖非負矩陣分解（Multiview Nonnegative Matrix Factorization，MultiNMF）［28］、共正則化譜聚類（Co-regularized multi-view Spectral Clustering，CoregSC）［29］、協同訓練譜聚類Co-train［30］、基于一致圖的多視圖聚類（Graph-based Multi-View Clustering，GMC）以及自適應鄰居多視圖聚類（MLAN）。在表3 中對比了本文算法與上述多視圖聚類算法的時間復雜度。

表3 時間復雜度對比Tab.3 Time complexity comparison

為了評估該算法的性能，本文采用三個常見的評價指標：精度（Accuracy，ACC）、歸一化互信息（Normalized Mutual Information，NMI））和純度（Purity）來衡量實驗效果。此外，為了評估各個算法在癌癥數據集上的效果，本文采用了經驗p值衡量癌癥樣本分組后的生存差異［31］，p值越低，表示不同組間的生存差異越顯著。

3.3 實驗結果分析

表4～6 分別列出了本文算法與其他聚類算法在仿真數據集及6 個真實數據集上的ACC、NMI、Purity 結果。觀察表4～6可知，對于評價指標ACC，本文算法在每個數據集上都取得了最好的結果。

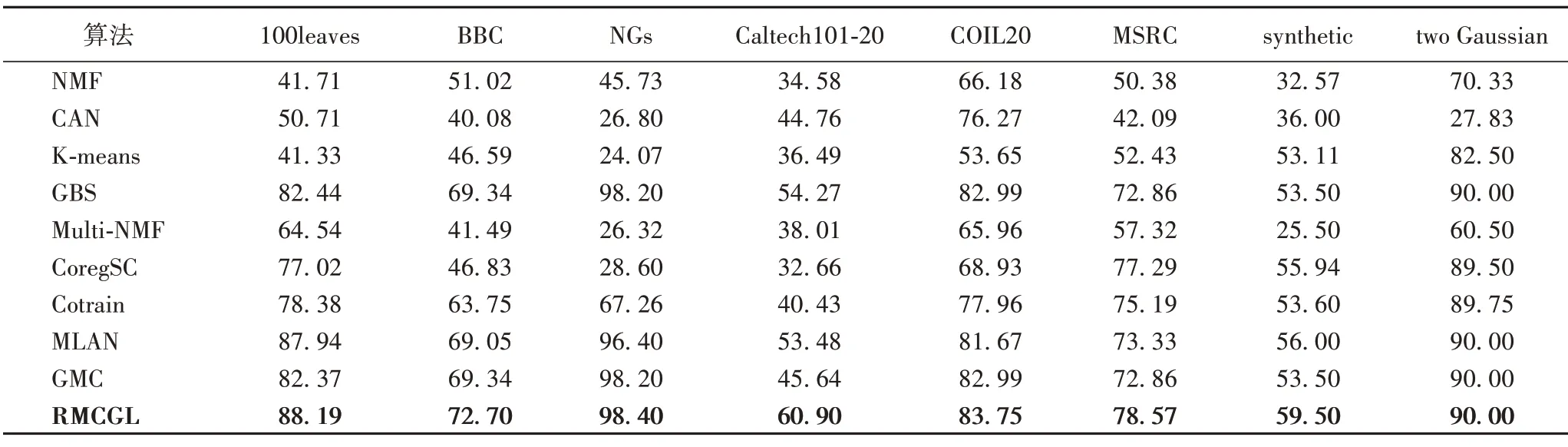
表4 不同聚類算法在不同數據集上的ACC值 單位：%Tab.4 ACC values of different clustering algorithms on different datasets unit：%

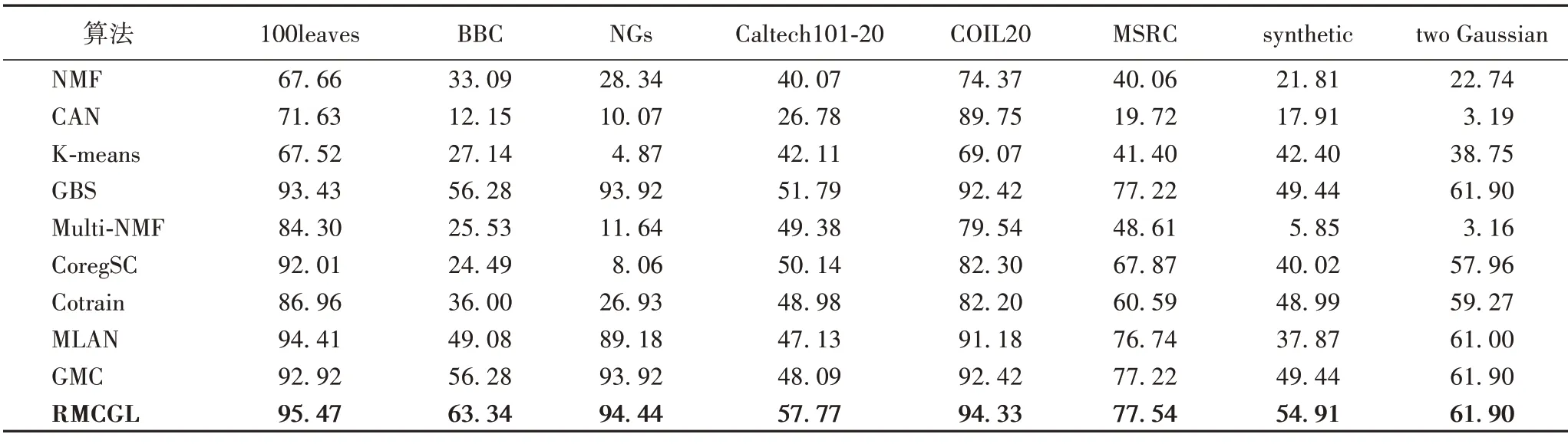
表5 不同聚類算法在不同數據集上的NMI值 單位：%Tab.5 NMI values of different clustering algorithms on different datasets unit：%

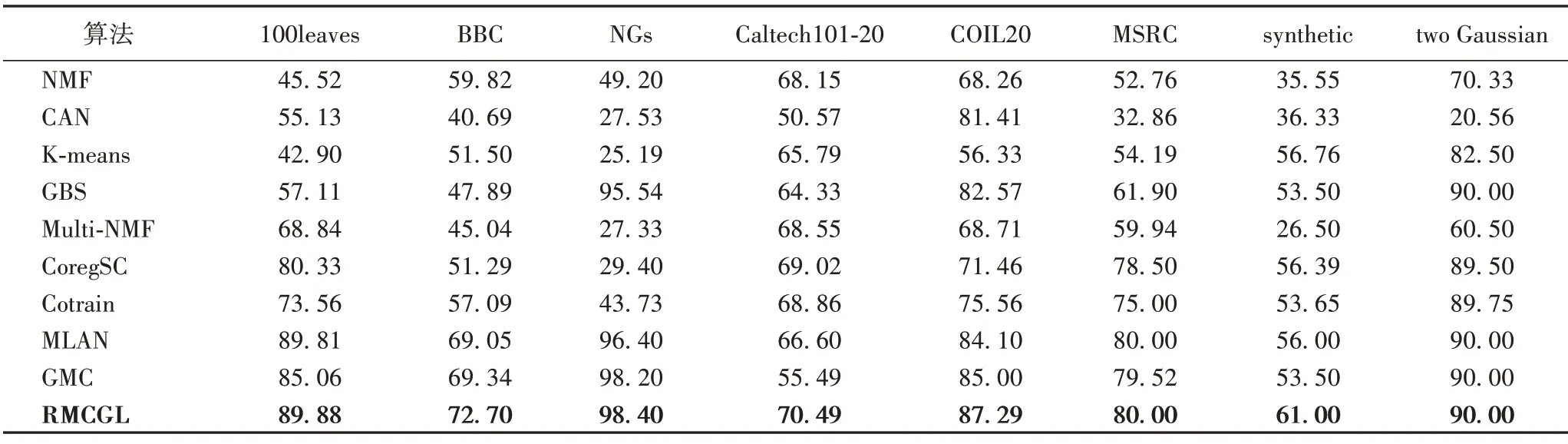
表6 不同聚類算法在不同數據集上的Purity值 單位：%Tab.6 Purity values of different clustering algorithms on different datasets unit：%

表7 給出了各對比算法在4 個癌癥數據集上經驗p值的實驗結果，同時圖2 給出了RMCGL 算法在GBM 與Melanoma數據集上的生存分析曲線。與上述多視圖聚類算法相比，RMCGL 算法在所有的癌癥數據集上都得到了顯著的p值（p?value＜0.05），并且在四組癌癥數據集上的結果都是最顯著的。這些結果充分驗證了本文算法的有效性及良好的泛化能力。

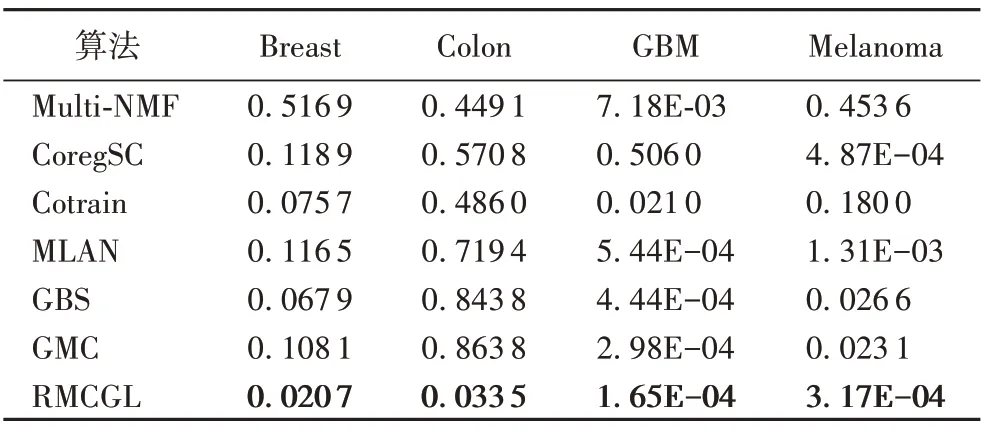
表7 四個癌癥數據集上經驗p值比較Tab.7 Comparison of empirical p-values on four cancer datasets

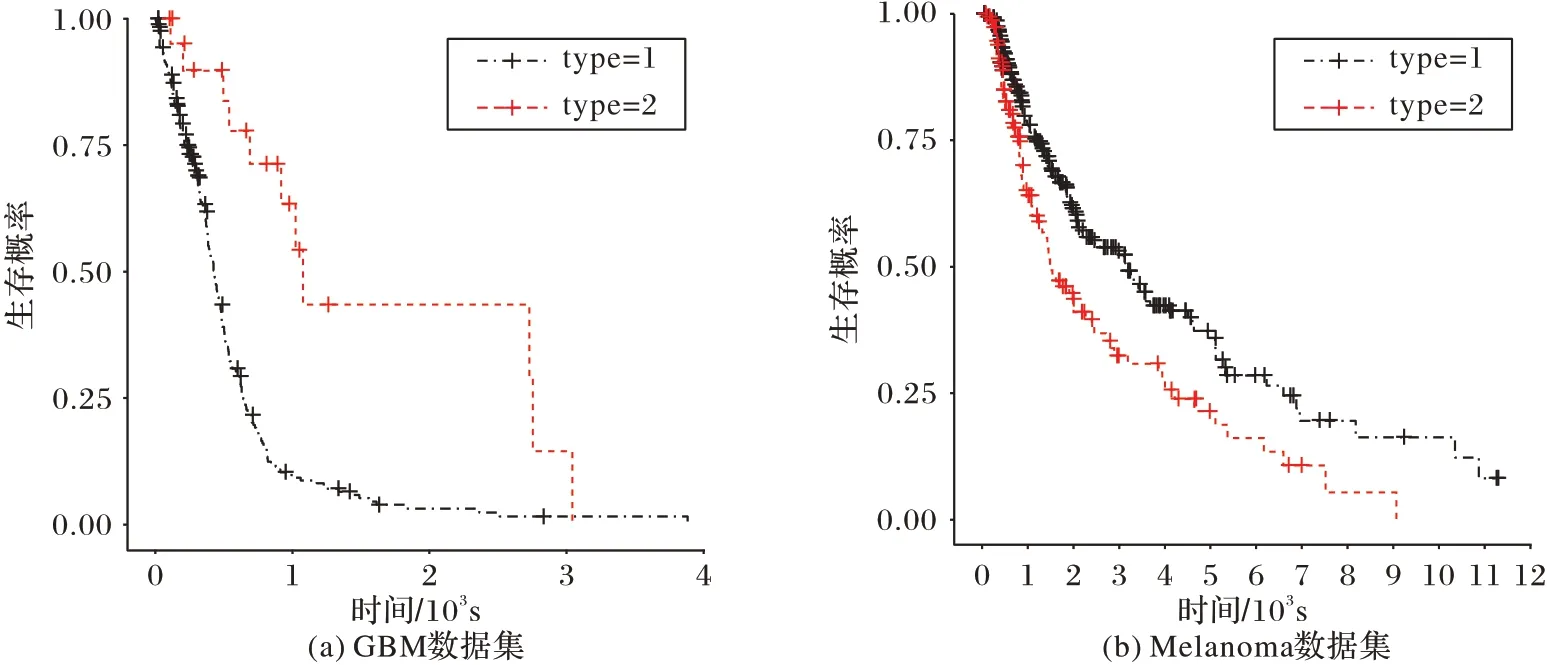
圖2 RMCGL算法在GBM與Melanoma數據集上的生存分析曲線Fig.2 Survival analysis curve of RMCGL algorithm on GBM and Melanoma datasets

圖3 為RMCGL 在NGs 和two Gaussian 數據集上學習得到的一致圖G對應的熱圖，從圖中可以清晰地看到一致圖的塊對角結構，這說明算法能學習一個高質量的相似度圖結構。

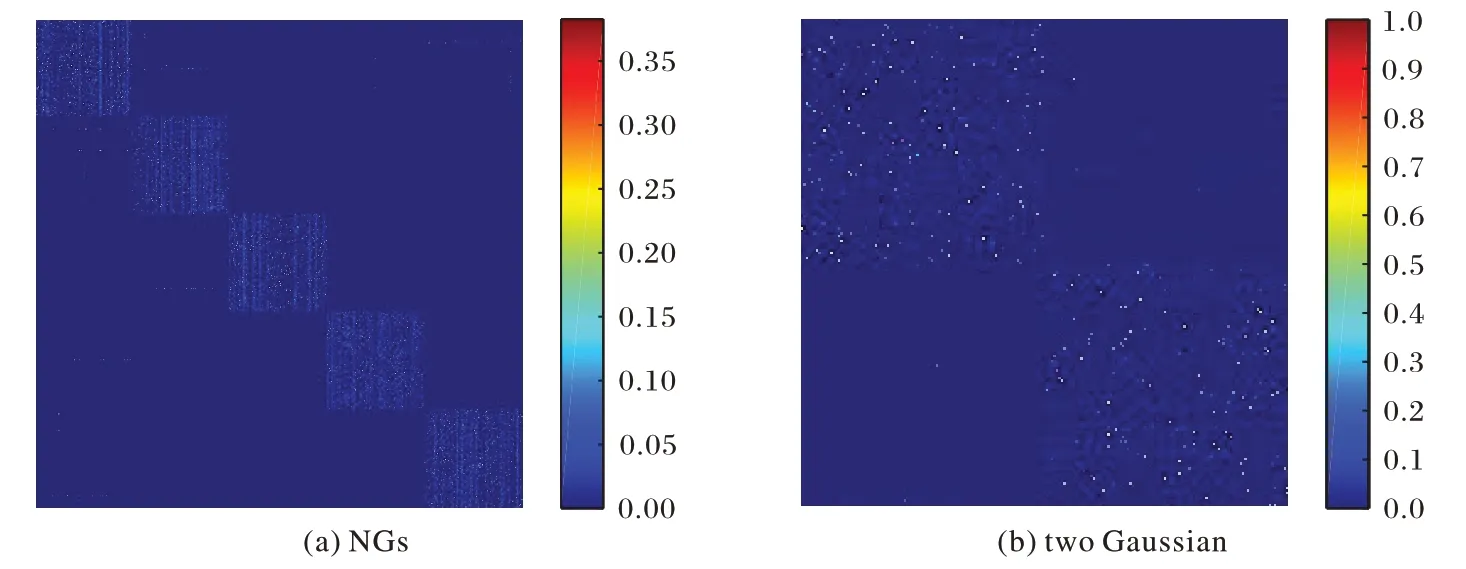
圖3 RMCGL學習得到的一致圖G在NGs和two Gaussian 數據集上的熱圖Fig.3 Heat maps of the consistency graph G learned by RMCGL on NGs and two Gaussian datasets

3.4 消融實驗分析

本文RMCGL 算法中創新性地引入了秩約束和魯棒表示學習，為了驗證算法各部分對實驗結果的影響，設計了對應步驟的消融實驗。取表4 中4 個數據集的ACC 值所對應的參數進行消融實驗的對比分析，主要驗證秩約束、相似度矩陣學習和魯棒表示學習對算法結果的影響。將去掉秩約束時的過程稱為RC；直接從不同視圖的魯棒表示學習中學習一個一致圖的過程為RL。此外去掉魯棒表示學習時，該算法即為GMC算法，本文算法與前者的區別在于，前者從原始數據集中學習不同視圖的相似度矩陣，而RMCGL預先學習原始數據的魯棒表示作為相似度學習的輸入。結果如表8 所示，從表中可以看出，在分別去掉秩約束、表示學習和相似度學習后的實驗結果明顯差于RMCGL 的結果，尤其在NGs 數據集中，添加秩約束后的結果提升了超過30個百分點；在MSRC數據集中，根據表示矩陣學習一致圖時的結果比該算法結果低20 個百分點左右。去掉表示學習時的結果見表4。由此可見，對學習到的一致圖施加秩約束、子空間魯棒表示學習以及根據魯棒表示矩陣學習不同視圖的相似度矩陣進而得到一致圖的過程對實驗結果都做出了貢獻。

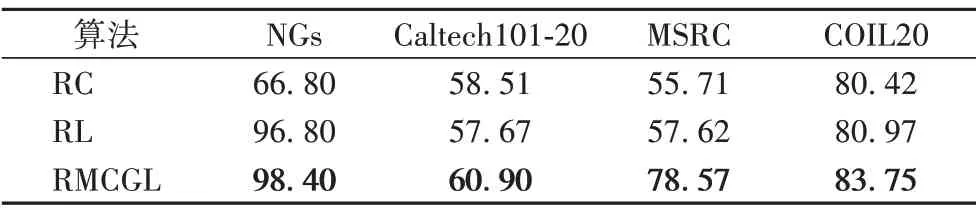
表8 消融實驗ACC結果 單位：%Tab.8 ACC results of ablation experiments unit：%

3.5 魯棒性性能評估

為了驗證RMCGL算法對實驗結果的魯棒性，設計了以下實驗：將誤差正則化項部分去掉，得到如圖4 所示結果。從圖4 中可以看出，在固定參數的情況下，去掉誤差正則化項部分后的4 個數據集的ACC 結果都有一定程度的下降，但整體下降幅度偏小，這表明RMCGL算法對數據具有較好的魯棒性。

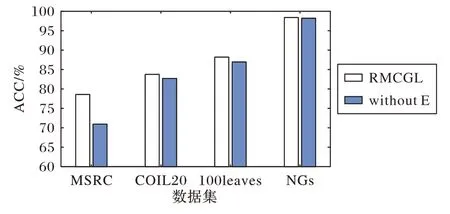
圖4 去掉誤差正則化項后在固定參數時各數據集的ACC結果Fig.4 ACC results of different datasets at fixed parameters after removing error regularization term

3.6 收斂性分析

本節分析了RMCGL 算法的收斂性，如圖5所示，圖中的x軸和y軸分別表示迭代次數和目標函數的值。從圖5 中可以看出，本文經過少量迭代后就可以達到穩定的收斂狀態。

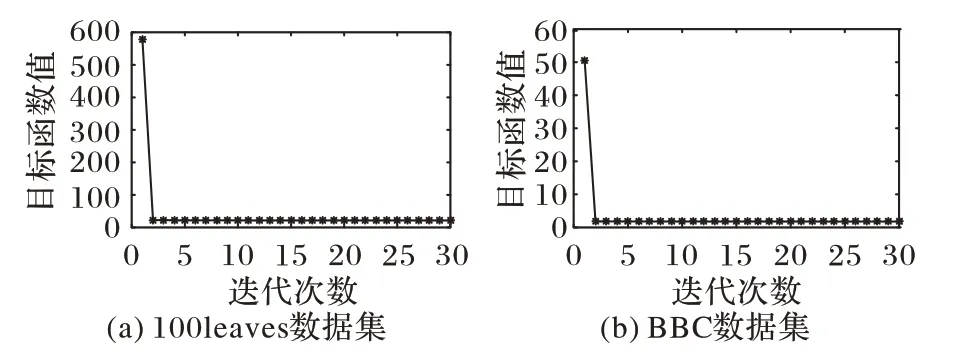
圖5 RMCGL算法在100leaves和BBC數據集上的收斂曲線Fig.5 Convergence curves of RMCGL algorithm on 100leaves and BBC datasets

3.7 參數敏感性分析

RMCGL算法中共有三個參數λE、λA和λC。為了分析這三個參數對算法性能的影響，將其中一個參數固定后分析另外兩個參數變化對NMI 值的影響，見表9～10。三個參數在所有數據集上的取值范圍均為［0.01，0.1，1，10，100］。

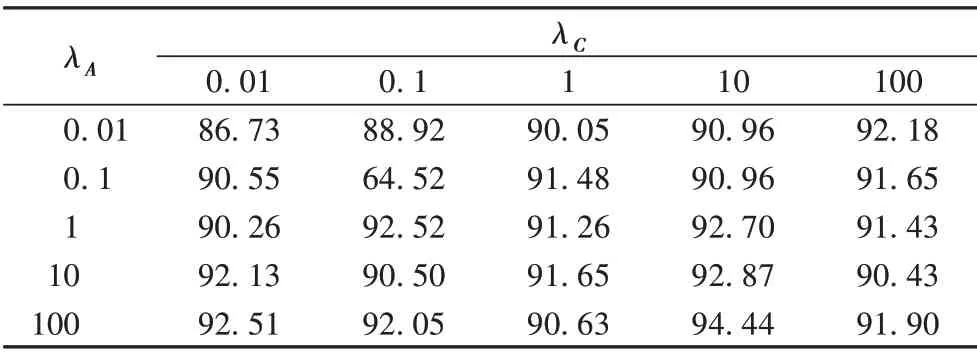
表9 NGs數據集NMI值隨參數變化分析Tab.9 Analysis of NMI value of NGs dataset with parameter variation

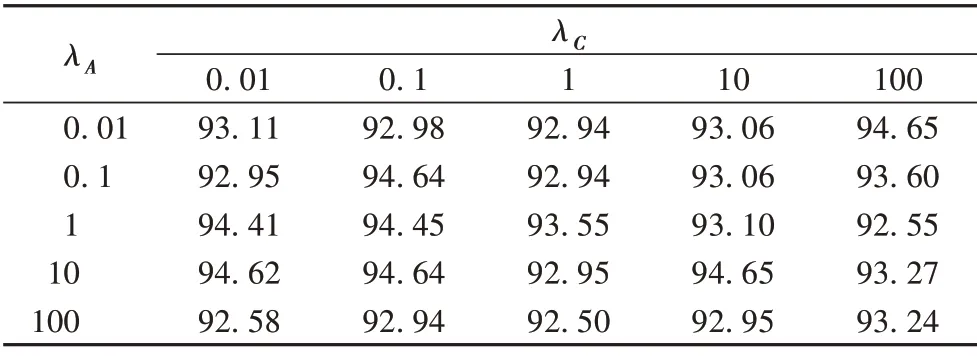
表10 COIL20數據集NMI值隨參數變化分析Tab.10 Analysis of NMI value of COIL20 dataset with parameter variation

圖6 展示了λE在兩個數據集上的參數分析結果。在NGs數據集中，當λA和λC的值取（0.01，0.01）時，固定這兩個參數，得到NMI相對于λE這個參數時的取值范圍：當λE取1時的效果最好，NMI的值為93.40%；而在取0.01時最小，NMI的值為86.73%。在COIL20 數據集中，λA和λC取（1，1）時固定，λE為0.01 時NMI 的最大值93.55%，而隨著參數值的增大，NMI的取值范圍變化平穩。從圖中可以看出，算法對于參數的變化相對較為魯棒。

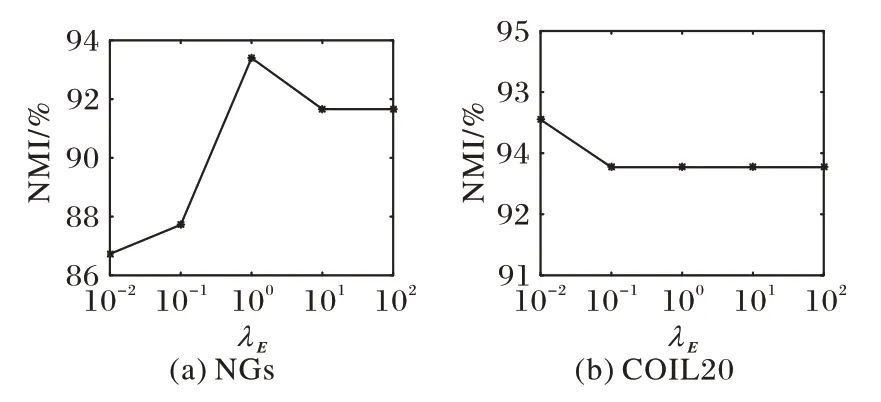
圖6 RMCGL算法在NGs和COIL20數據集上的參數分析Fig.6 Parameter analysis of RMCGL algorithm on NGs and COIL20 datasets

4 結語

近年來，多視圖聚類在許多領域得到了應用。多視圖數據比傳統的單視圖數據提供了更豐富的信息來揭示內部結構，并能獲得更好的聚類效果。本文首先簡要回顧了多視圖聚類算法，然后提出了一種新的基于一致圖學習的魯棒多視圖子空間聚類算法RMCGL。該算法通過學習數據的子空間表示來避免原始數據集中噪聲的干擾，并基于該表示構建不同視圖下的相似度矩陣；同時引入自加權策略，根據不同視圖的重要性合理分配視圖權重，并構造一個統一的一致圖；通過對一致圖的拉普拉斯矩陣施加秩約束直接獲得聚類結果，而不需要引入額外的聚類步驟。在多個數據集上的實驗結果驗證了RMCGL算法的有效性，相比其他多視圖聚類算法有明顯優勢。