基于核非負矩陣分解的有向圖聚類算法

陳 獻，胡麗瑩*，林曉煒，陳黎飛，3

（1.福建師范大學計算機與網絡空間安全學院，福州 350117；2.數字福建環境監測物聯網實驗室（福建師范大學），福州 350117；3.福建省應用數學中心（福建師范大學），福州 350117）

（?通信作者電子郵箱hlyxyz@fjnu.edu.cn）

0 引言

圖結構可以自然地表示網狀結構的數據，如社交網絡、電力網絡、引文網絡、運輸網絡、蛋白質-蛋白質相互作用網絡［1］等。隨著各個領域網絡數據的增長以及對網絡數據處理的迫切需求，分析圖結構以及挖掘圖結構中的關系信息成為了熱點問題，圖聚類［2］是其中的一項基礎研究課題。圖聚類根據節點及節點間連接關系的相似性將節點劃分為簇，使得簇內節點相似度較高，簇間的節點則差異較大。

目前已提出多種圖聚類算法，包括基于圖分割的算法［3］、層次聚類算法［4］、譜聚類算法［5］等，這些算法大多忽視節點連邊的方向性，把有向圖轉化為有無向圖進行處理。對于有向網絡如引文網絡、基因轉移網絡、運輸網絡等，若以無向圖方式處理將丟失有用信息甚至引發歧義。例如，對于由文獻間引用和被引用關系構成的引文網絡，當看作無向圖時，將出現文獻間僅存在的單方面引用關系變成同時包含引用和被引用雙向關系的錯誤情形。為有效建模節點間連接關系的方向性，目前典型的方法是將無向圖聚類算法推廣到有向圖，如Satuluri 等［6］提出的轉換有向圖為無向加權圖的方法，通過有向圖上非對稱鄰接矩陣隨機游走對稱化或節點的入度和出度對稱化手段來構造新的對稱鄰接矩陣，但這種方法可能導致有向圖上某些獨特的邊方向性信息丟失。基于Laplacian 矩陣的多種譜聚類算法［7-9］則將聚類目標函數擴展到有向圖中，并對得到的拉普拉斯矩陣做特征值分解；但該矩陣的特征值可能存在負值，降低了所構造模型的可解釋性。

基于非負矩陣分解（Nonnegative Matrix Factorization，NMF）［10］的一類方法［11-12］則通過將圖鄰接矩陣的非負結構分解（structured factorization）實現圖聚類。由于被分解的可以是非對稱矩陣且分解結果均為非負矩陣，該類方法對有向圖聚類具有良好的適應性和可解釋性，近年來得到廣泛關注。譬如，Wang 等［11］提出的非對稱非負矩陣分解（Asymmetric NMF，ANMF）算法將有向圖的非對稱鄰接矩陣分解為分別表示“節點-簇”隸屬度和簇間相似性的非負矩陣，進而基于隸屬度矩陣對節點進行簇劃分；在此基礎上，Tosyali等［12］引入節點間的相似先驗信息為正則項，構造了正則化的非對稱非負矩陣分解（Regularized Asymmetric NMF，RANMF）算法，提高了有向圖聚類的準確性和魯棒性。

然而，以上算法忽略了有向圖上潛在的節點間的非線性關系。在許多實際應用產生的圖（網絡）中，節點與節點之間通常是非線性相關的。如社交網絡中，個體（節點）之間的關系并不是單一的，有可能是同事、家人甚至更復雜的人際關系（有向邊）。顯然，這些關系不能簡單地以線性方式來逼近。當前，深度學習（deep learning）與核學習（kernel learning）是兩種主流的節點間非線性關系建模方法。例如，Perozzi 等［13］提出深度游走（DeepWalk）算法，通過隨機游走捕捉圖的高階近鄰結構，進而將深度學習技術運用到圖聚類問題中；但是，該算法并未考慮節點間連接的方向性。核學習方法［14］通過將低維數據嵌入到高維核空間中，使得低維不可分數據在新空間中線性可分或接近線性可分，從而有效挖掘隱含在數據中的非線性關系。近年，已提出多種核非負矩陣分解（Kernel NMF，KNMF）算法，利用小樣本條件下核學習方法在非線性學習中的良好性能進行人臉識別、文本聚類等［15-18］。

本文提出用于非線性有向圖聚類的核非負矩陣分解算法，稱為正則化的核非對稱非負矩陣分解（Regularized Kernel Asymmetric NMF，RKANMF）。首先，基于核化機制構造了有向圖核聚類目標函數，定義了約束核空間中節點相似性關系的正則化項，以保持原空間中節點間相似關系的同時強化核空間中同簇節點間的（非線性）相似性；其次，基于梯度下降法提出了一種聚類優化算法，證明了算法的收斂性；最后，在8個有向網絡數據集上進行了實驗，并與深度學習算法等進行了對比，實驗結果驗證了所提算法的有效性。

1 相關工作

1.1 基本定義

定義1有向圖。在有向圖中G=(V，E)，邊(i，j)∈E將節點i連接到節點j，|V|表示節點數，|E|表示邊數。有向圖可以由鄰接矩陣來表示。

構建有向圖鄰接矩陣：鄰接矩陣A∈Rn×n+，其中n是節點數，若從節點到節點存在有向邊，[A]ij=1，否則[A]ij=0。特別地，[A]ii=0。本文用[·]ij表示矩陣第i行第j列元素。

圖聚類基于節點間的相似性：節點之間越相似，則越可能劃分到同一個簇。文獻中常用的節點相似性度量有：

1）Katz 中心相似性度量［19］。對于圖中每一條路徑，利用加權方案計算其權重，公式如下：

其中：I為元素全為1 的矩陣；當參數β＜1 時，較長的路徑將分配到較小的權重，較短的路徑則獲得更大的權重，權重越大，節點間就越相似。

2）余弦相似性度量［19］。計算節點間公共鄰居的數量，公共鄰居的數量越多表示節點間越相似。計算公式為：

其中：cij表示節點i與節點j的公共鄰居數量；為由所有鄰居數量組成的向量的長度，取值在0到1之間。余弦相似度為1表示兩個節點具有相同的鄰居，0則表示沒有相同鄰居。

1.2 基于NMF的聚類算法

其中：r?min{m，n}為分解矩陣的秩；‖?‖F表示矩陣的Frobenious 范數。對于聚類任務［20］，分解結果中的W可以視為隸屬度矩陣，根據規則將第i個樣本xi分配到隸屬度最大的簇j*，完成聚類。

下面介紹兩種基于NMF 的代表性有向圖聚類算法：ANMF［12］和RANMF［13］算法。ANMF 將式（3）中的B矩陣用HWT代替，其中，，定義其優化問題如下：

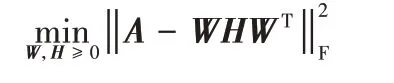
RANMF 在ANMF 算法基礎上添加了圖正則化項，對同簇節點間的相似性進行約束，其定義的優化問題如下：

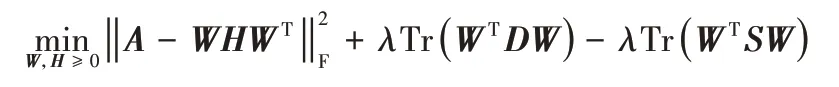
其中：Tr(?)是矩陣的跡；S是節點間相似性矩陣；D為對角矩陣，其中每個對角元Dii是矩陣S的第i行元素的和。

1.3 核函數與KNMF

核函數是從低維空間到高維空間中的一種映射函數。設R為輸入空間，H為特征空間（希爾伯特空間或核再生空間，以下簡稱核空間），核學習方法［14］利用核函數實現從R到H的映射：φ(X)：R→H。對于輸入空間的樣本對(xi，xj)，核技巧（kernel trick）通過替換核空間中樣本對的內積為核函數κ(xi，xj)的值（核化），解決φ(X)難于計算的問題，即：

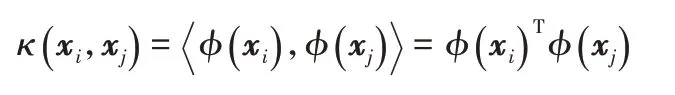
常用的核函數包括多項式核函數和徑向基核函數等，其定義分別如下：

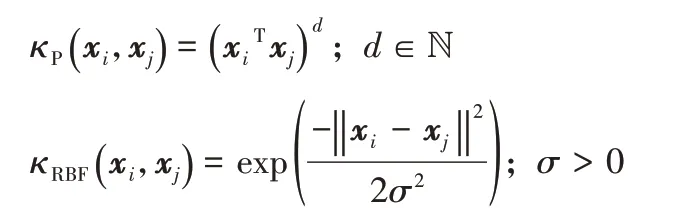
為捕捉數據中的局部結構信息，文獻［21］新近提出了分數階核（Fractional power kernel）：

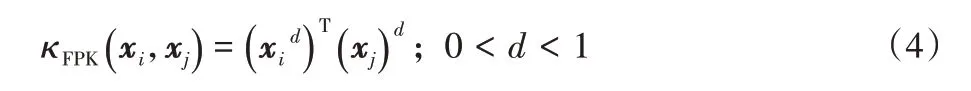
其中：zd表示任意向量z中每個元素的d次冪。鑒于圖聚類的目的在于根據圖的局部結構特性進行節點分組，本文采用如式（4）所示的分數階核函數，并用矩陣形式加以表示，如下：

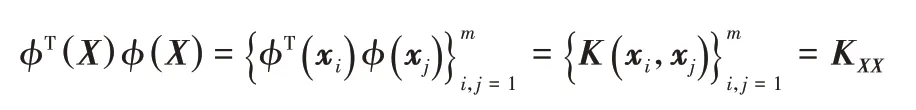
在傳統NMF 的基礎上，利用上述核化機制可以對輸入矩陣進行核非負矩陣分解（KNMF）。例如，基于KNMF 的人臉識別［17-18］定義其優化問題為：

意在優化兩個非負矩陣W和B，使得映射后的人臉圖像在核空間可以近似地表示為基圖像的線性組合，即：φ(X)≈φ(W)B。相比僅能對數據中線性關系建模的傳統NMF，KNMF 的優勢在于可以通過核函數對數據進行高維映射發掘隱含的非線性特征，并利用核技巧降低算法的時間復雜度。

2 RKANMF有向圖聚類算法

本章討論基于正則化核非對稱非負矩陣分解（RKANMF）的有向圖聚類算法。首先構造了新的聚類優化目標函數，給出參數優化方法；接著，提出優化該目標函數的聚類算法，并嚴格證明了算法的收斂性。

2.1 聚類目標函數及其優化方法

為在保持原空間中節點間（線性）相似關系的同時強化核空間中同簇節點間的（非線性）相似性，在構造約束核空間中節點相似性關系的正則項的基礎上，利用核化機制定義RKANMF有向圖核聚類目標函數如下：

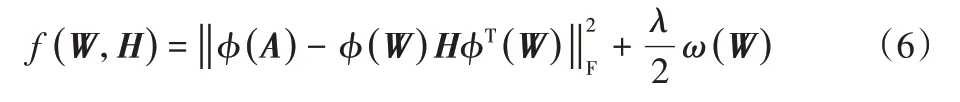
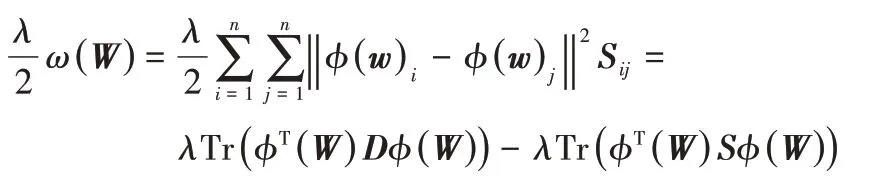
其中：D是對角線矩陣，其對角元Dii是矩陣S的第i行的和。整理聚類目標函數式（6）得到：

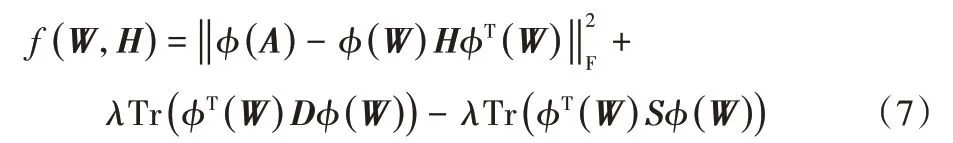
從優化角度分析，聚類是求解聚類目標函數最優值的過程，即在矩陣W和H非負約束條件下最小化式（7）。根據梯度下降方法，矩陣W和H通過迭代以下乘法更新規則求解：

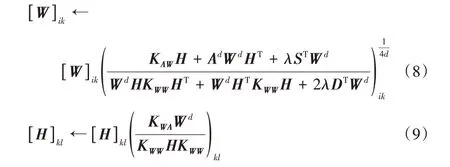
其中Zd表示矩陣Z中每個元素的d次冪。

2.2 聚類算法及收斂性分析

依據2.1 節中W和H的更新公式（式（8）和（9）），提出基于RKANMF的有向圖聚類算法，具體描述如下：

算法 基于RKANMF的有向圖聚類算法。

計算KWAWd和KWWHKWW的時間復雜度分別為O(n2r)和O(r2(r+n))，由于r＜n，每次迭代更新公式H的時間復雜度為O(n2r)。同理，每次迭代更新W的時間復雜度為O(n2r)，因此，算法在不考慮迭代次數的情況下，時間復雜度為O(n2r)。

接著對算法的收斂性進行分析，借鑒文獻［11，22］中的輔助函數法來證明在所提更新規則下算法的收斂性。

定理1式（7）中的目標函數在矩陣W和H的更新規則式（8）和（9）下是單調非增的。

證明 當固定H時，令

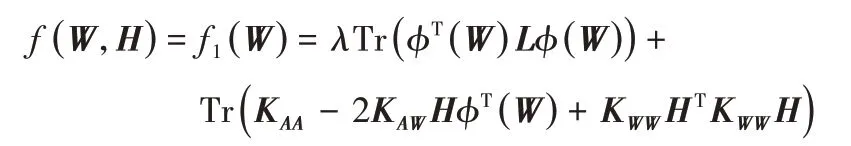
可得以下三個不等式：

令φ(W)=Wd，即得式（8）中W的更新公式。

同理，當W固定時，正則項部分與H無關。此時，令

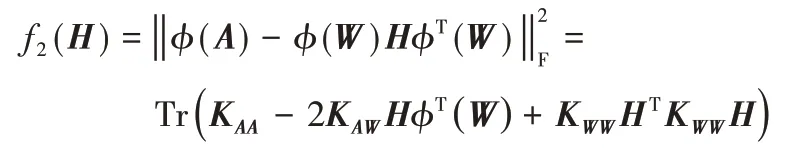
則有：

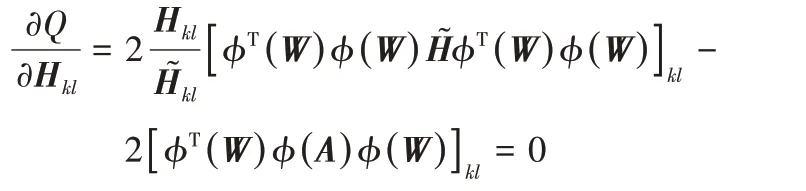
得出式（8）中H的乘法更新公式。又由于

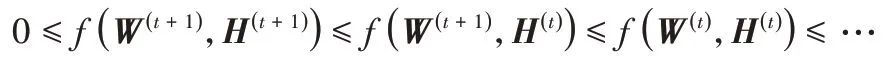
3 實驗與分析

本章通過在三個領域有向網絡數據集上的實驗來驗證所提算法RKANMF 在有向圖聚類中的有效性，并與當前若干主流算法（ANMF［11］、RANMF［12］及DeepWalk 算法［13］）進行對比。實驗平臺如下：Core i7-9750 2.60 GHz CPU，16.00 GB 內存，操作系統為Windows 10。

3.1 數據集

實驗使用的有向網絡數據集包含專利-引文網絡（Patent Citation Network，PCN）數據集［23］、World Wide Knowledge Base（WebKB）數據集［24］和人工合成網絡LFR（Lancichinetti-Fortunato-Radicchi）數據集［25］，數據集的詳細信息見表1。

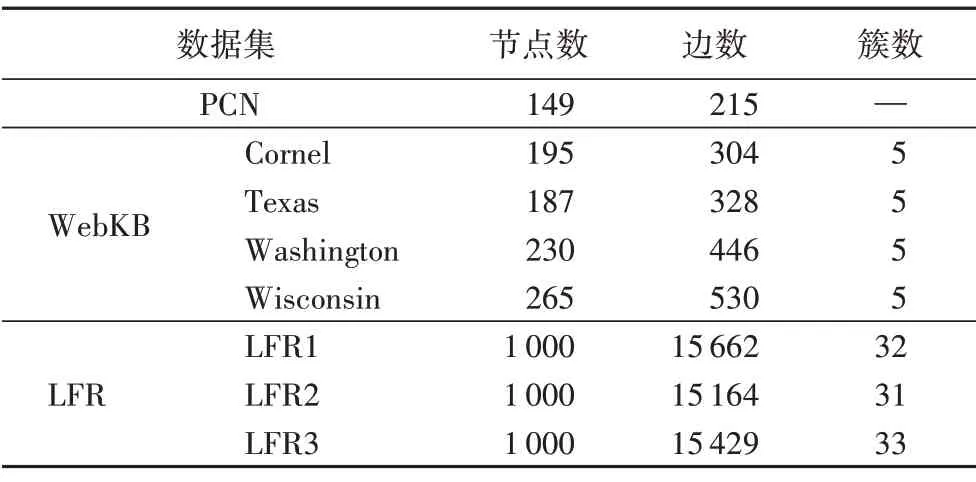
表1 有向網絡數據集的詳細信息Tab.1 Details of directed network datasets

①PCN 數據集。PCN 由4 142 個節點和18 385 條邊組成，形成一個單一的連接樹結構。本文選擇PCN 中的149個節點（專利）和215 個有向邊（引用）來檢驗聚類效果。由于同一簇的專利不一定具有直接公共鄰居，而是具有一個或多個中間專利連接的非中間鄰居，因此根據式（1）計算相似矩陣。由于PCN數據集沒有提供節點標簽，因此該數據集的簇數目未知，表1用“—”給予了標識。

②WebKB 數據集。該數據集包含從4 所大學（Cornel、Texas、Washington 和Wisconsin）收集的網頁，網頁分為學生、課程、項目、教師和工作人員5 類。通常，一個高質量的簇應具有較少的簇間連接和更多的簇內連接。由于WebKB 數據集中的簇與簇之間的連通性較高，選用式（2）計算節點間的相似矩陣。

③LFR 數據集。LFR 是一個人工合成數據集，包含的網絡是根據某些參數控制的機制產生的。比如，通過混合參數μ控制合成網絡中簇間連通性的強度，其值越大意味著更強的簇間連通性。本文取μ=0.1，0.3，0.5（分別對應表1 中的LFR1、LFR2 和LFR3），并使用Katz 中心相似性度量式（2）計算節點間的相似矩陣。

3.2 評價指標

當數據集沒有真實簇劃分時采用Davies-Bouldin（DB）指標［26］和Distance-based Quality Function（DQF）指標［27］評價多個算法的聚類結果質量；當存在真實簇劃分時采用聚類準確率（ACcuracy，AC）指標、NMI 指標及Jaccard 指標［28］。各指標簡要介紹如下：

①DB指標。

計算簇內散射與簇間分離之比，公式如下：

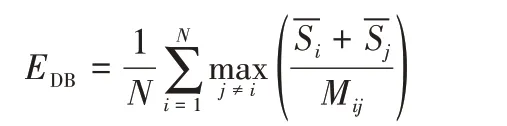
其中：N表示簇的個數；表示第i個簇中節點的平均分散程度；Mij為第i類與第j類簇的距離。當DB 指標值越小時，算法得到的聚類效果越好。

②DQF指標。

計算簇與簇之間的平均距離，公式如下：

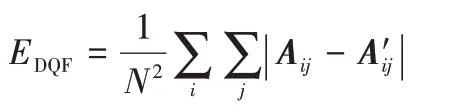
其中：A表示鄰接矩陣；是根據算法得到節點簇集合劃分r個簇后構建的新鄰接矩陣，若節點i與j同簇，則。DQF指標越高，則得到的聚類結果越好。

③AC指標。

計算預測的節點簇集合的準確率，公式如下：

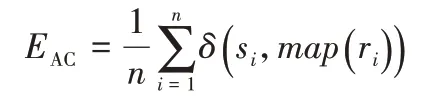
其中：n表示節點個數；ri、si分別為第i個節點所對應的獲得的標簽和真實標簽；map(ri)是一個映射函數，表示將ri映射到相應的節點簇類上。δ是指示函數，其公式如下：

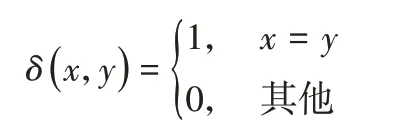
AC指標越高，聚類質量越高。

④NMI指標。

計算預測的節點簇集合與真實節點簇劃分的相似度，公式如下：

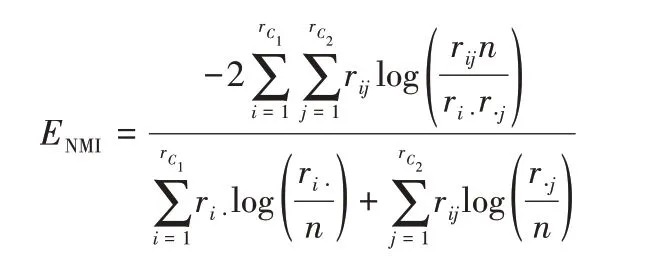
其中：C1和C2分別是預測的節點簇集合與真實節點簇集合；分別表示真實簇的數目與預測簇的數目；矩陣R=代表混淆矩陣，rij為真實簇的節點i出現在發現簇j的數量，ri?和r?j分別是混淆矩陣第i行的和與第j列的和。NMI指標越高則聚類質量越好。

⑤Jaccard指標。

計算預測的節點簇集合與真實節點簇集合的交集和并集之比，公式如下：

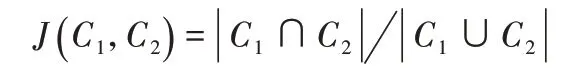
其中：C1表示預測的節點簇集合，C2為真實節點簇集合。Jaccard指標越高，則得到聚類結果與真實簇劃分越相似。

3.3 參數設置

為檢驗本文RKANMF 算法是否能有效建模節點間的非線性關系，將它與ANMF算法［11］、RANMF算法［12］進行了比較，并通過對比DeepWalk算法［13］，檢驗了小樣本條件下算法對有向聚類的準確性。

在對不同網絡數據集的實驗中，RANMF 算法與ANMF 算法中Katz 中心相似性度量的β參數以及懲罰項權重系數λ的設置與文獻［12］中的最佳參數一致，所有基于NMF 的算法統一設置迭代停止精度ε=10-6。DeepWalk 算法參照文獻［13］設置每個節點出發游走10 次，游走長度為10；skip-gram 模型設置詞向量的維度為30，窗口大小設置為7。

簇的數目r值是有向圖聚類算法的重要問題，也是各個算法需要設置的先驗參數，本文在具有類標簽的數據集上采用真實簇的數目作為r值，對于沒有類標簽的PCN 數據集，選取不同的r值來對算法性能進行測試。

在真實網絡數據集中（PCN 和WebKB 數據集）重點討論分數階核的次冪d值與懲罰項權重系數λ值對RKANMF 算法的影響。在PCN 數據集的實驗中，為了與ANMF 與RANMF算法進行對照實驗，RKANMF 算法設置共同的參數λ=0.1，β=0.2。當參數d值取得過小時，計算過程中，W的更新公式（8）中的分母可能會接近于0，因此選擇d值在0.2 到0.9 區間。圖1與圖2顯示當簇數r=2，d=0.2時，RKANMF 算法在DB與DQF指標上均取得最優。隨著d值增加，越趨近于1時，算法不再對節點間的非線性關系建模，從而導致聚類質量下降。為檢驗簇數不同時對算法的影響，統一設置參數d=0.2。

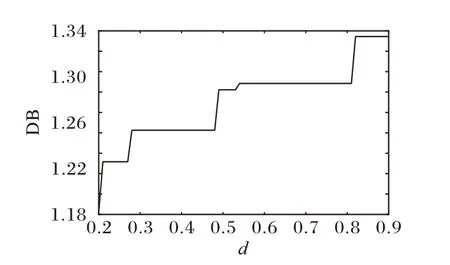
圖1 參數d對DB指標的影響Fig.1 Influence of parameter d on DB index

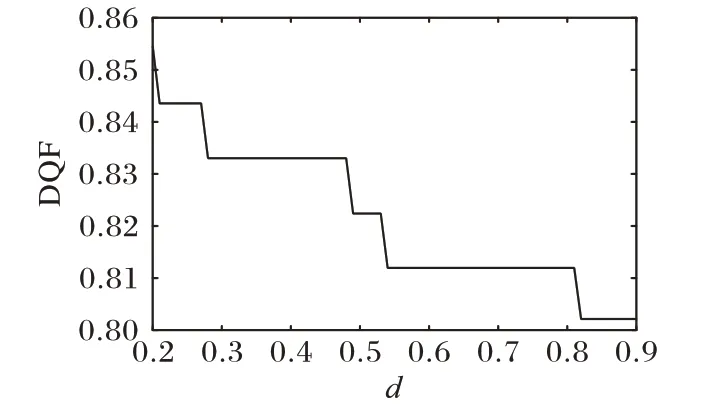
圖2 參數d對DQF指標的影響Fig.2 Influence of parameter d on DQF index

在具有真實簇劃分的WebKB 數據集實驗中，著重考慮d值在0.2 到0.9 區間變化時，RKANMF 算法對AC 指標的影響。結果如圖3所示，在多個子數據集上，當d值在0.4到0.5之間時，算法的聚類結果在AC 指標上更高。當d值趨于1 時AC指標呈下降趨勢，算法不再建模節點間的非線性關系從而導致聚類質量下降。根據圖3，對四個子數據集（Cornel、Texas、Washington 和Wisconsin）分別取合適的d值為0.4、0.4、0.9和0.5。

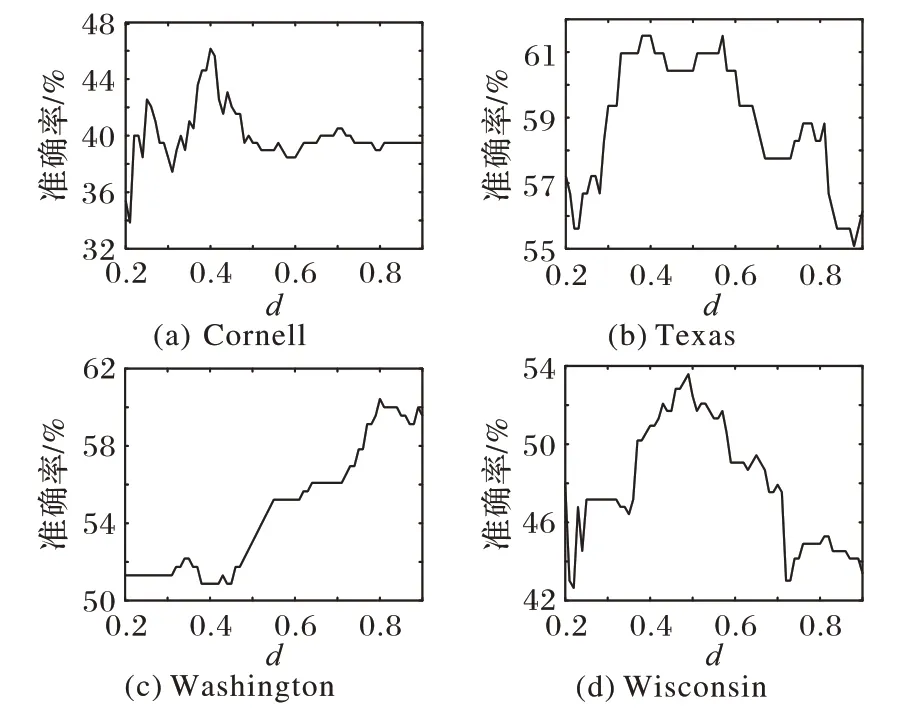
圖3 WebKB數據集上d值對AC指標影響Fig.3 Influence of d value on AC index on WebKB dataset

為考慮λ值對算法的影響，當固定d值后，設置權重系數λ值區間為0 到500。圖4 顯示，當λ值越大時，算法越傾向于考慮節點間的相似性信息；當λ值過大時，算法過于依賴節點相似性，將原來屬于不同簇的節點劃分到同一簇中從而導致聚類準確性下降。根據圖4，對四個子數據集（Cornel、Texas、Washington 和Wisconsin）分別取合適的λ值為20、5、50 和20。同理，在LFR 的3個數據集中，所提算法通過對比多次得到的AC指標值，設置合適的參數β=0.1，λ=0.1，d=0.88。

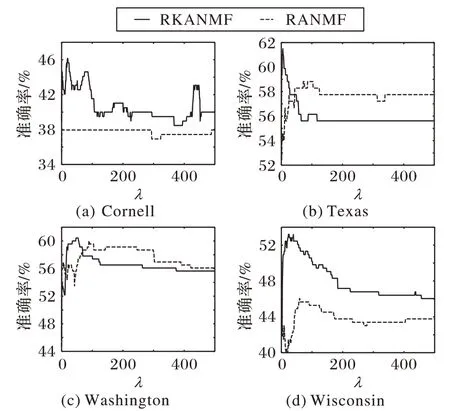
圖4 WebKB數據集中λ值對AC指標影響Fig.4 Influence of λ value on AC index on WebKB dataset

3.4 PCN數據集的實驗結果對比分析

本節使用PCN 數據集［23］來檢驗四種算法的性能表現。表2 是利用DB 和DQF 指標上對不同算法進行比較的結果。方便起見，表中均采用“Rnd”對隨機初始化策略進行標識；用“SVD”表示基于SVD策略［12］的初始化，方法與文獻［12］一致；使用隨機初始化策略的算法運行100 次，每一次都按不同的初始化矩陣進行迭代，取最終結果的平均值。

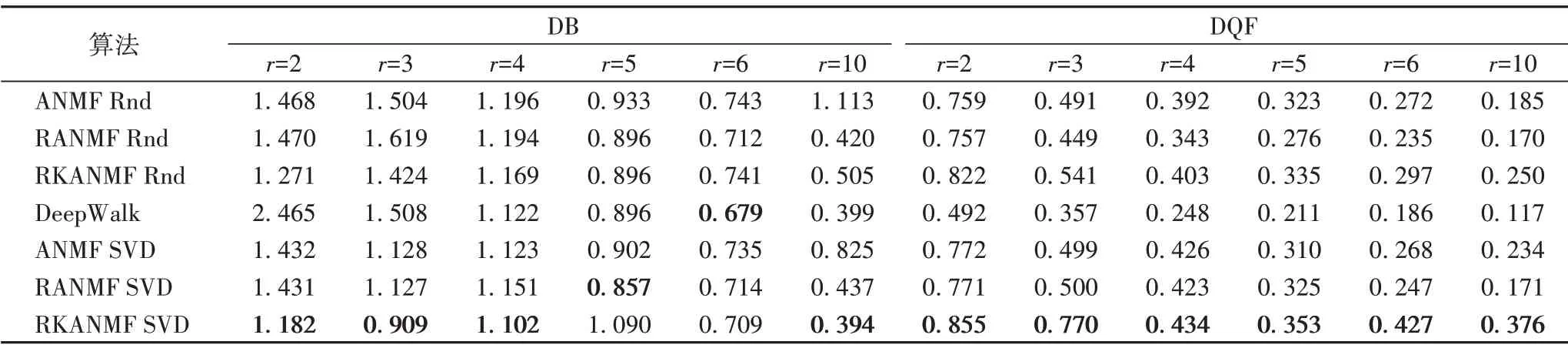
表2 簇數（r）不同時各算法在PCN上的DB和DQF指標比較Tab.2 Comparison of DB and DQF indexes on PCN for each algorithm with different number of clusters（r）

表2 結果表明，隨著簇數r的增加，所有算法的聚類質量均有所下降，說明當簇的數目r越來越多時，本應該劃分到相同簇的節點被分到不同簇，導致聚類質量降低。對于DB 指標，當簇數r=6 時，RANMF 算法與RKANMF 算法的DB 指標均低于DeepWalk 算法，這是由于過多考慮非中間鄰居從而導致聚類效果變差。對于DQF 指標，在隨機初始化的情況下，所提算法也能比基于SVD 策略初始化［12］的RANMF 與ANMF算法在DQF 指標上取得更好的表現。這說明RKANMF 算法有效地對節點間的非線性關系建模得到了更好的特征表示，顯著提高了聚類質量。對比三種基于NMF 的算法可知，好的初始化策略及考慮了非線性關系的NMF 算法均能避免分解過程陷入較差的局部最優值。

3.5 WebKB數據集的實驗結果對比分析

本節使用WebKB 數據集［24］中的四個子數據集來檢驗幾種算法在數據集的簇間連通性強時的性能，結果如表3。可以看出，當數據集簇間連通性較高時，基于隨機初始化策略的算法能得到較好的聚類結果，這是由于經過多次隨機初始化的過程，算法更容易找到一個更好的局部極小值。對比基于NMF 的算法與DeepWalk 算法可知，在大多數情況下，基于NMF 的算法能得到更好的聚類結果。這說明當圖的結構變得模糊，DeepWalk 算法無法準確獲取有向圖的高階近鄰結構，從而導致聚類質量下降。

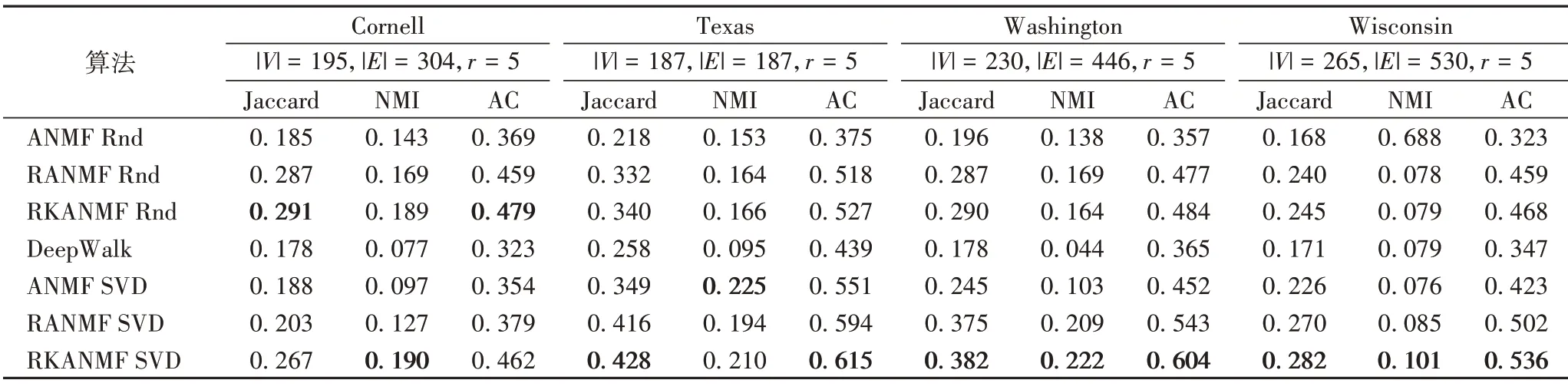
表3 各算法在WebKB數據集上的結果比較Tab.3 Result comparison of different algorithms on WebKB dataset

在Cornell 子數據集中，RKANMF 算法在NMI 指標上最高，表明在數據集的簇間連通性高的情況下，RKANMF 算法也能有效發掘節點間非線性關系。在Texas 子數據集中，RANMF 與RKANMF 算法的NMI 指標低于ANMF 算法，因為在正則項權重系數逐漸變大的過程中，帶正則項的兩個算法均忽視了鄰接矩陣的結構信息，從而聚類質量下降。

3.6 LFR網絡數據集的實驗結果對比分析

本節使用LFR網絡［25］來檢驗幾種算法檢驗在度分布不平衡的復雜網絡中的表現，結果如表4。表4顯示了不同算法在LFR 網絡上的實驗結果，其中“—”表示基于SVD 策略初始化的ANMF算法得不到聚類結果。由表4可以看出，隨著μ值的增加，算法對簇的劃分變得愈加困難。當簇類結構變得模糊時，基于NMF 的算法在NMI 指標上低于DeepWalk 算法，這說明DeepWalk 更有針對性地獲取圖的結構來提高劃分簇的質量。RKANMF 算法在AC 和Jaccard 指標上有更好的表現，這是由于RKANMF 算法中正則項發掘了節點間的（非線性）相似性關系。相比其他基于NMF 的算法，RKANMF 不僅在NMI指標上與DeepWalk 算法比較接近，且在AC 和Jaccard 指標上有顯著的提高，這說明當節點關系變得復雜時，對節點間的非線性關系進行建模能更有效地提高聚類算法的表現。

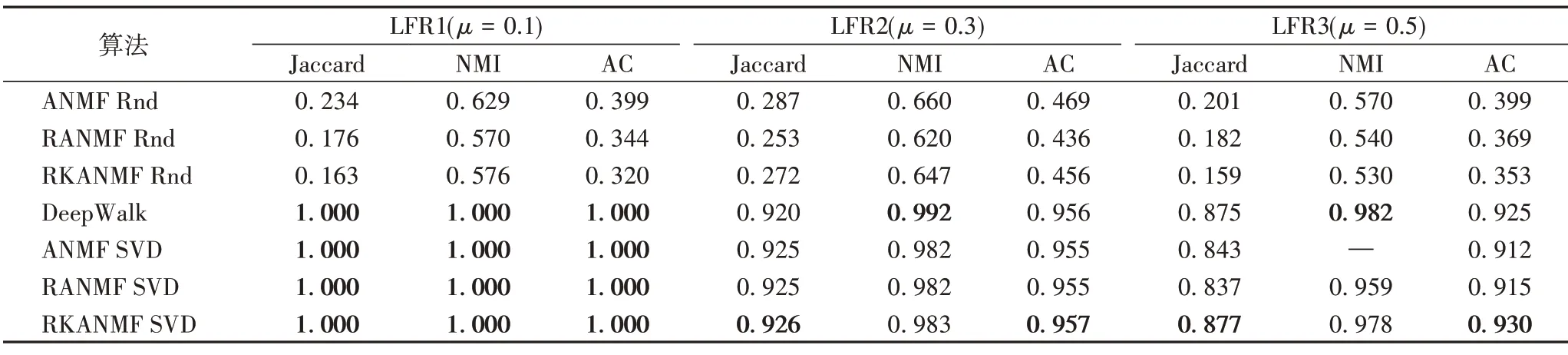
表4 各算法在LFR網絡數據集上的結果比較Tab.4 Result comparison of different algorithms on LFR network dataset

4 結語

本文提出了一個用于有向圖聚類的圖正則化核非對稱非負矩陣分解優化方法。該方法基于核化機制構造了有向圖聚類新目標函數，其正則項同時考慮了原始空間中節點間的相似性及節點在核空間中的（非線性）相關性；基于梯度下降法推導了一個有向圖聚類（RKANMF）算法，給出了算法的詳細過程及收斂性分析，并在多個有向網絡數據集進行了實驗。實驗結果表明，與未結合核學習方法的非負矩陣分解算法及DeepWalk 等算法相比，新算法在多個聚類有效性指標上有更好的表現。今后我們將針對性地考慮節點的方向性以及不同核函數對有向圖聚類的影響等方面做進一步研究。