基于蟻群-遺傳融合框架的倉儲群機器人任務分配①

梁金琳, 薛頌東, 趙 靜, 潘理虎

1(太原科技大學 計算機科學與技術學院, 太原 030024)

2(廣東機電職業技術學院, 廣州 510515)

以亞馬遜Kiva機器人為代表的智能倉儲揀貨技術, 將傳統的“人到貨”模式革命性地升級為“貨到人”模式, 極大適應了現代物流配送發貨單位小型化的特點[1].倉庫規模擴大和訂單數激增, 進一步要求提升揀貨效率, 由此提出了面向智能倉儲調度的群機器人任務分配問題[2].其屬于一類NP-Hard問題[3], 通常采用啟發式算法解決.Azadnia等[4]借鑒旅行商問題的求解思路,用遺傳算法對訂單任務進行排序, 使分揀人員走過的路程最短, 但其復雜性隨任務量增加顯著提高.沈博文等[5]將機器人狀態設置為“忙”“閑”兩種, 通過修正A*算法實現特殊道路條件約束下的倉儲調度, 但該法僅適合小規模任務情形.郭宇[6]提出一種基于市場拍賣思想的多機器人任務分配方法, 通過性能差值的直觀比較, 確定各機器人的競標價格, 生成較優的任務分配方案.該法雖回避了組合和整數規劃中的復雜運算,適合較大數量子系統之間的交互, 但對通信要求較高.蔣家志等[7]使用一種改進的微粒群算法(PSO)解決訂單調度問題, 主要優化目標為同一訂單中所有任務的完工時間與該訂單總完工時間的相聚程度, 提高了智能倉儲的運行效率, 但未考慮機器人的平均利用率, 可能導致部分機器人負擔過重.楊杰[8]引入訂單池概念,以訂單池中與分揀臺上訂單的適應度為標準, 使用離散PSO生成各分揀臺上的任務執行順序.該法在處理大規模訂單時, 容易產生早熟收斂現象, 且局部尋優能力較差, 無法找到最優分配規則.李功捷[9]引入虛擬任務概念和任務數分配思想, 通過智能優化算法求解智能倉儲調度的機器人任務分配問題.

每種群體智能算法各有優缺點.發揮各自優勢,提高求解效率, 是不同算法融合的動機.作為經典的啟發式算法, 許多學者對蟻群算法和遺傳算法的融合進行了大量研究, 以克服或抑制各自缺陷, 實現優勢互補.融合算法大體上分為兩類: 一類是以蟻群算法為主體,利用遺傳算法產生的結果作為信息素進行尋優[10].該法雖能夠改善蟻群算法初期信息素匱乏的問題, 但在遺傳算法階段一旦陷入局部最優, 后續的蟻群算法將很難跳出, 且蟻群算法本身也很可能因收斂速度過快陷入局部最優.為解決該問題, 在固定次數迭代后又引入遺傳操作, 加大種群分布多樣性, 但花費的時間代價高, 不適合實時應用場景[11].另一類是以遺傳算法為主體, 利用蟻群算法快速收斂的特性進行問題求解[12], 提高了全局尋優能力, 但主要用于求解旅行商問題.

本文在前人研究的基礎上, 根據智能倉儲調度中多訂單任務動態產生、任務由群機器人并發執行的特點, 將問題建模成群機器人協同調度的多目標優化問題.利用蟻群算法產生的較為優秀的解集, 作為遺傳算法的初始種群, 以加快遺傳算法的收斂速度.在遺傳算法中采用多層編碼, 以適應群機器人任務分配需求, 在輪盤賭算子后引入精英保留策略, 對選擇算子進行改進, 并增加逆轉算子, 在保證種群多樣性的同時, 使最優個體能夠直接遺傳到下一代.通過多種技術手段的綜合運用, 設計了一種新的蟻群-遺傳算法融合框架.仿真結果表明, 在本文提出的融合框架中求解, 較分別使用蟻群算法或遺傳算法求解, 能夠明顯發揮蟻群算法魯棒性好和遺傳算法全局搜索能力強的特點, 且算法性能穩定, 有效提高智能倉庫的整體運行效率.

1 問題描述

如圖1所示, 由貨架、移動機器人、分揀臺等組成智能倉儲系統, 設置有出入口與外界相通, 機器人能將訂單上商品對應的貨架按照一定次序送至分揀臺,由等候的倉庫工作人員按系統指示從貨架上取出相應數量的商品, 放入訂單對應的包裝箱中打包配送.現有一批訂單, 包含貨物的品類數為n, 要求由m個成員機器人組成的群機器人處理.假設倉庫為封閉的二維空間, 一個貨架上只存放一種商品, 則可用貨架位置表征特定品類商品對應的任務, 記任務集C= {1, 2, …,n}.設i,j為貨架(任務)編號,i,j∈C, 機器人從貨架i運動到j的距離為Dij, 倉庫中空閑機器人的數量為r.規定成員機器人執行的最少任務數為L.對環境進行柵格化建模[13].考慮機器人避碰, 貨架間設置兩條通道, 供機器人相向通行.將各柵格設置的二維碼視為路標, 用于機器人定位.為簡便起見, 追加如下假設:

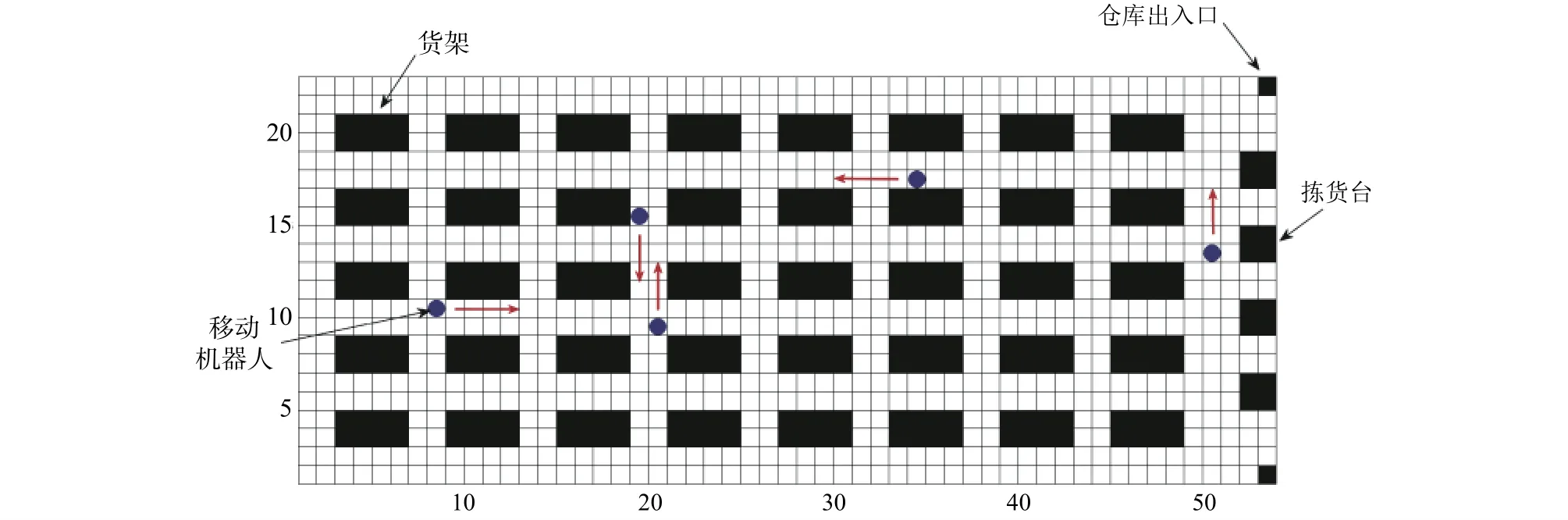
圖1 簡化的智能倉儲系統

(1) 每個機器人占據一個柵格, 以柵格為單位移動,運動方向限定為上、下、左、右.

(2) 為避免機器人碰撞, 貨架區域間由柵格組成的通道均為單行道.

(3) 機器人的感知、定位、交互、運算、運動, 以及托舉重物的能力相同.

群機器人的任務分配流程為: 中央處理器接收到訂單任務, 查表得到商品所在貨架位置, 生成機器人的調度方案; 機器人運動到相應貨架并將其托舉至分揀臺; 分揀臺處等候的工作人員按訂單要求取下貨架上的商品; 機器人將貨架送回原位置, 該次任務完成.

對于一個訂單任務, 由于商品種類及貨架位置均已確定, 故機器人在貨架與分揀臺間的行走距離也已確定.這便意味著, 群機器人任務分配的優化目標, 為機器人完成相應于時序相連的兩個任務(貨架)的過程.由于機器人只能沿柵格移動, 記柵格位置坐標(x,y),故貨架之間的距離用曼哈頓距離計算, 見式(1):

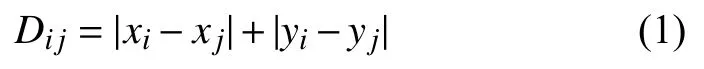
其中,xi,yi和xj,yj分別為第i, j個任務對應貨架在柵格地圖中的橫坐標和縱坐標.

根據智能倉儲系統的優化目標, 將任務分配評價指標定義為路徑代價和時間代價的綜合.其中, 路徑代價為機器人在目標任務間行走的距離.構造如式(2)所示的適應度函數, 作為評價指標:

其中,PAC為路徑代價, 即完成所有任務全部機器人走過的距離之和;TAC為時間代價, 即全部機器人完成所有任務花費的時間;A,B是路徑代價和時間代價的權重.由于完成任務花費的時間與機器人的行走距離有關, 故將完成任務時行走距離最大的機器人走過的距離值作為時間代價.為避免誤解, 同時作距離量綱到時間量綱的處理.可見, 適應度函數值越小, 表明完成任務的代價越小, 即全部機器人完成任務走過的距離越短, 任務分配越合理.

2 蟻群算法求解任務分配問題

用蟻群算法[14]建模并求解任務分配問題.螞蟻之間通過覓食過程中釋放的“信息素”進行間接通信, 選擇較優路徑, 形成正反饋, 經過多次迭代找到最優路徑.

表示任務數和機器人數的符號意義保持不變.將其轉化為(n+m-1)個任務的單機器人問題.由于機器人的能力相對有限, 故限定機器人執行的最大任務數為lr.首先給每只螞蟻隨機分配一個初始任務, 待初始任務完成, 將其加入禁忌表, 然后從未完成的任務中選擇一個.當第r個機器人完成的任務數等于最大任務數lr時, 螞蟻選擇下一個機器人執行其余任務, 直到所有任務完成為止.t時刻螞蟻k由任務i到j的狀態轉移概率見式(3):

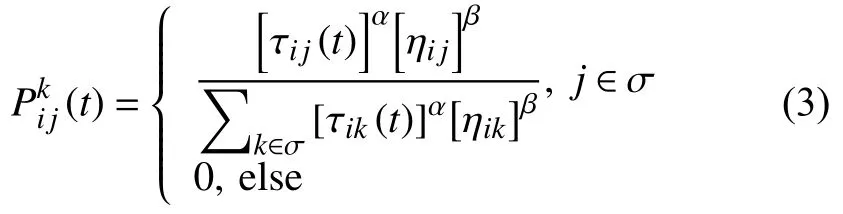
其中, τij(t)表示任務i和j之間的信息素強度, ηij表示任務i和j間啟發式因子的強度, α、 β 分別是信息素重要程度因子和啟發函數重要程度因子, 用于調節τij(t)和 ηij之間的作用, σ表示機器人還未完成的任務, 即不在禁忌表中的任務.t+n時刻螞蟻釋放的信息素濃度,按式(4)所示規律更新:

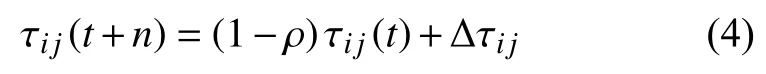
其中, ρ為信息素揮發因子, ( 1 -ρ)則為信息素殘留因子, Δ τij為本次循環任務i到j的信息素增量, 見式(5):

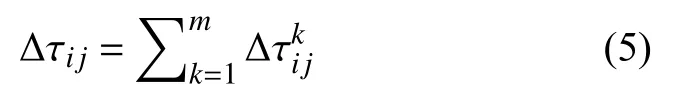
其中,Q為信息素強度系數,Lk表示第k只螞蟻本次循環所走過的路徑長度.群機器人任務分配求解的蟻群算法流程見算法1.

算法1.蟻群算法解決任務分配開始參數初始化隨機產生m只螞蟻的初始位置當不滿足終止要求:對于每一只螞蟻k:根據式(3)計算狀態轉移概率選擇任務更新禁忌表結束當m只螞蟻搜索完畢:記錄本次迭代最佳路線按式(4)-式(6)更新信息素禁忌表清零結束結束

3 遺傳算法求解任務分配問題

用遺傳算法[15]求解群機器人任務分配問題.為解決收斂速度慢和封閉競爭問題, 定義虛擬任務并加入列表.為了使虛擬任務不影響代價計算, 規定虛擬任務間的關聯代價為無窮, 虛擬任務與真實任務間的代價以及虛擬任務的自身代價為0.群機器人任務分配的遺傳算法求解流程見算法2.

算法2.遺傳算法解決任務分配開始初始化參數初始化種群中m條染色體編碼當不滿足終止要求:計算個體適應度值遺傳操作結束解碼輸出最優結果結束

4 蟻群-遺傳融合框架及其求解

4.1 基本思想

蟻群算法具有較強的魯棒性, 對初始路線要求不高, 求解結果不依賴于初始路線選擇, 但收斂速度慢,易陷入局部最優, 且計算開銷大.遺傳算法全局搜索能力強, 不會陷入局部最優解的快速下降陷阱, 但搜索速度較慢, 對初始種群依賴性強, 局部搜索能力差.為發揮兩種算法各自的優勢, 提高收斂速度和執行效率, 提出一個蟻群-遺傳算法融合框架.基于該框架的群機器人任務分配算法流程見算法3.

算法3.蟻群-遺傳算法融合框架內的群機器人任務分配開始初始化參數隨機產生m只螞蟻的初始位置對于每一個螞蟻k:根據式(3)計算狀態轉移概率選擇任務更新禁忌表結束當m只螞蟻搜索完畢:將蟻群算法一次迭代所得解集作為遺傳算法初始種群種群編碼當不滿足終止要求:根據式(2)計算個體適應度值do{輪盤賭法從種群中選擇一定比例父代精英保留策略選出最佳父代直接保存其余個體分別進行交叉、變異、逆轉操作}結束獲得任務分配最優解結束

不難看出, 融合框架的設計思路為, 利用蟻群算法,經過一次迭代后產生一個較為優秀的解集, 將其作為遺傳算法的初始種群, 以有效減少遺傳算法的尋優次數, 快速找到最優解.

4.2 操作要點

(1) 種群初始化.遺傳算法的初始種群通常是隨機生成的, 雖然保證了個體的多樣性, 但隨機生成的初始種群在迭代過程中收斂速度緩慢, 導致遺傳算法尋優速度慢.本文將蟻群算法經過一次迭代后產生的解集作為遺傳算法的初始種群, 使遺傳算法獲得較為優秀的初始種群, 有效減少遺傳算法的尋優次數.

(2) 編碼.遺傳算法采用多層編碼方式, 第1層編碼為任務的執行順序, 第2層編碼為機器人之間執行任務中斷點的位置.

(3) 選擇算子.采用輪盤賭法選擇一定比例的父代,再通過精英保留策略, 挑選出最佳父代, 直接保存在下一代中.采用這種方法可以在保證個體多樣性的同時,還可以使最佳個體直接遺傳到下一代中.

(4) 交叉算子.采用部分映射交叉方式, 在染色體編碼串中隨機選擇兩個交叉點, 然后進行部分基因的交換, 得到新的個體.

(5) 變異算子.采用互換變異的方式, 隨機選擇兩個基因位置, 然后將這兩個基因位置的編碼交換, 獲得一個新的個體.染色體中基因互換過程見圖2.

圖2 變異算子操作過程

(6) 逆轉操作.為加速進化加入逆轉操作, 這里的逆轉操作具有單向性, 即加入逆轉操作后產生的個體更優才會進行.隨機產生兩個隨機數n1和n2(n1,n2∈n,n1≠n2), 將n1與n2間的基因反向排序, 得到新個體.以n=8,n1=3,n2=6為例的逆轉操作見圖3.

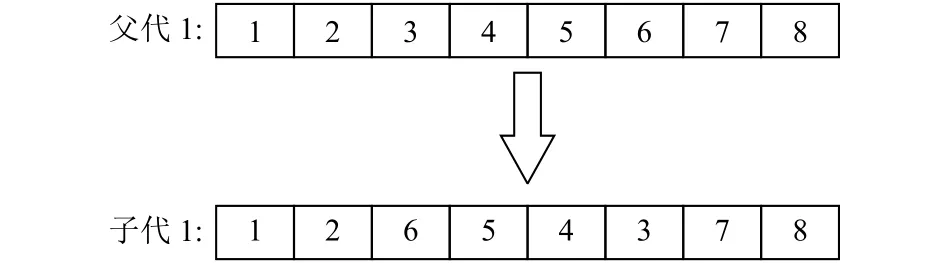
圖3 逆轉操作過程

5 仿真

仿真在Matlab 2018b的平臺上進行.將尺寸為100 m×102 m的實驗環境建模為柵格地圖, 單位長度為 1m.貨架的位置坐標設置后, 任務隨機生成.設置螞蟻數=80, 信息素重要程度因子α=1, 啟發函數重要程度因子β=5, 遺傳算法種群數=80, 最大迭代次數=5000.

考慮到倉庫存在空閑期和繁忙期, 分別用蟻群算法、遺傳算法和本文所提的融合算法, 針對小任務量和中大任務量情形, 進行任務分配實驗.

5.1 小任務量情形

設置空閑移動機器人數量=4, 隨機生成任務數=20,每個機器人執行5個任務, 分別使用蟻群算法、遺傳算法和融合算法, 對群機器人任務分配進行控制, 收斂過程見圖4.

圖4顯示, 融合算法在迭代300次左右時, 適應度函數值趨于穩定; 而蟻群算法和遺傳算法分別在在迭代4000和2000次后, 適應度函數值逐漸穩定于200左右.表明融合算法的收斂速度較蟻群算法和遺傳算法快, 且結果也優于其他兩種算法.究其原因, 融合算法在迭代開始時就有較為優秀的種群, 在迭代過程中可以快速跳出局部最優, 收斂性強, 適應度函數值接近于最終穩定的結果.因此, 對于小規模的任務分配, 本文所提融合算法能夠快速尋求較優的任務分配結果,進而提高智能倉庫的整體運行效率.

圖4 小任務量分配情形典型迭代過程(任務數=20, 機器人數=4)

5.2 中大規模任務量情形

(1) 固定任務數=100, 分別令機器人數=10, 20, 30,40, 50, 每組實驗重復執行30次, 統計結果見圖5.

圖5 不同規模群機器人完成100個任務的代價

結果顯示, 隨著機器人數量增加, 群機器人完成任務花費的路徑代價和時間代價逐漸降低.通過折線圖可以直觀看出, 本文提出的融合算法無論是走過的路程還是花費的時間, 都明顯優于單獨采用蟻群算法和遺傳算法時的任務分配效果, 體現出較高效率.在執行固定數量的任務時, 采用融合算法進行任務分配, 機器人完成全部任務花費的時間比單獨采用蟻群算法和遺傳算法少50%以上, 融合算法具有明顯優勢, 大大提高了智能倉庫的整體工作效率.在機器人數=10, 20, 30,40時, 融合算法的路徑代價呈現線性下降的趨勢; 當機器人數=50時, 下降趨勢減緩.其原因可能是, 隨機器人數增多, 倉庫中逐漸變得擁擠; 當執行任務的機器人過多時, 會導致每個機器人分配的任務數過少, 無法充分發揮機器人的價值, 造成資源浪費.

(2) 固定機器人數=10, 分別令任務數=50, 100, 150,200, 每組實驗重復執行30次, 統計結果見圖6.

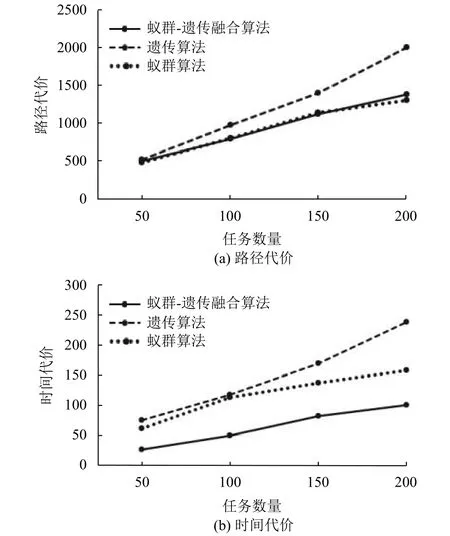
圖6 10個機器人分別完成不同數量任務的代價

不難發現, 群機器人數不變時, 隨著任務增加, 花費的路徑代價和時間代價都隨之增加.

使用融合算法和單獨使用蟻群算法進行任務分配,雖然在路徑代價上沒有明顯差別, 但前者的時間代價遠小于后者.在任務數超過150后, 采用遺傳算法進行任務分配花費的路徑代價和時間代價增加速度變快,完成任務機器人所走的路程以及花費的時間變大, 而融合算法則在任務數超過150后, 花費的路徑代價和時間代價增加趨勢減緩.

使用融合算法進行任務分配, 路徑代價和時間代價均優于單獨使用遺傳算法.

本組實驗結果表明, 本文提出的融合算法在中大規模智能倉儲系統的任務分配效率更高.

通過兩組實驗可以發現, 蟻群算法收斂速度慢, 易陷入局部最優, 且計算開銷大.遺傳算法搜索速度較慢,對初始種群依賴性強, 局部搜索能力差.采用融合算法進行任務分配, 相較單獨使用蟻群算法或遺傳算法, 時間代價明顯為少.隨著任務數增加, 融合算法體現出更高的效率.

計算兩種變量固定情形下的路徑相對誤差SP和時間相對誤差ST.計算方法見式(7)和式(8):

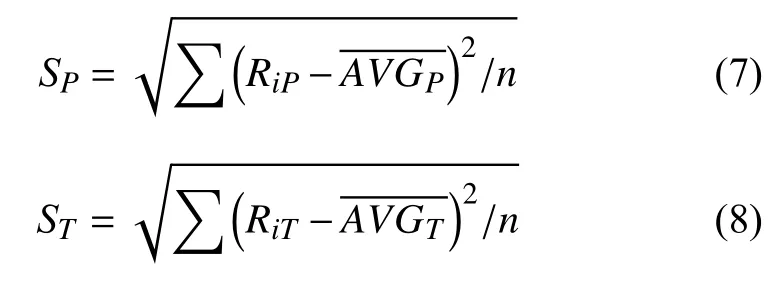
其中,RiP,RiT分別是第i次實驗的路徑代價和時間代價,分別是n次實驗路徑代價和時間代價的平均值, 結果見表1和表2中, ACO_GA_P, ACO_GA_T為融合算法分別對應的路徑代價和時間代價, GA_P,GA_T為遺傳算法分別對應的路徑代價和時間代價,ACO_P, ACO_T為蟻群算法分別對應的路徑代價和時間代價.

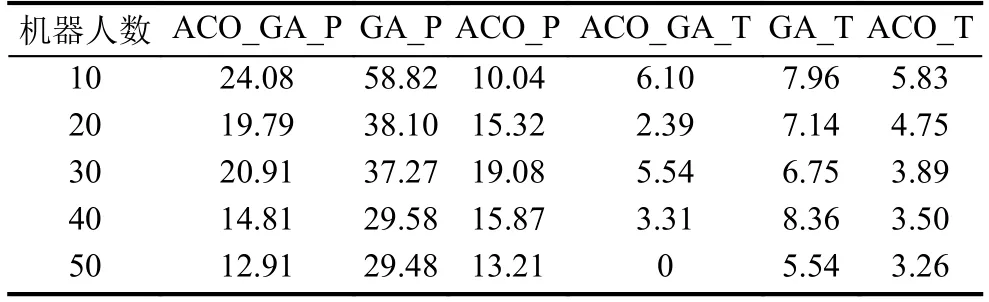
表1 不同數量機器人完成100個任務的相對誤差

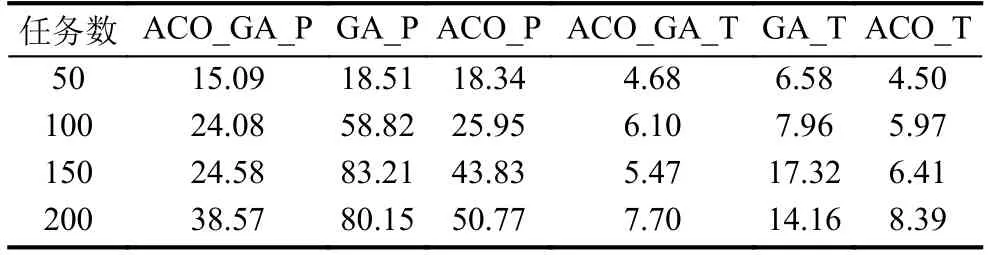
表2 10個機器人完成不同數量任務的相對誤差

結果顯示, 任務量確定時, 隨著機器人數增加, 相對誤差逐漸變小; 機器人數確定時, 隨著執行的任務數增加, 相對誤差逐漸變大.可見, 作為啟發式算法, 不同組合條件下都存在隨機性.但本文所提融合算法的代價, 其相對誤差均較單獨使用蟻群算法和遺傳算法更小, 表明融合算法的性能較為穩定.

6 討論

本文針對智能倉儲調度中群機器人任務分配問題,提出了一個適用于不同任務規模的蟻群-遺傳算法融合框架, 通過仿真實驗得到以下結論:

(1) 蟻群算法具有較強的魯棒性, 采用蟻群算法解決群機器人任務分配問題時對初始路線要求不高, 求解結果不受初始路線的影響, 局部搜索能力強.但蟻群算法收斂速度慢, 易陷入局部最優, 且計算開銷大, 故采用蟻群算法解決群機器人任務分配問題效率較低.

(2) 單獨使用遺傳算法解決任務分配問題, 全局搜索能力強, 不會陷入局部最優的快速下降陷阱, 但搜索速度較慢, 對初始種群依賴性強, 局部搜索能力差, 故單獨使用遺傳算法解決該類問題執行效率較低.

(3) 蟻群-遺傳算法融合框架下, 蟻群算法和遺傳算法各自優點得到發揮, 全局搜索能力強, 不會陷入局部最優解, 收斂速度快, 完成任務的路程代價和時間代價較小, 尋優結果更好, 提高了智能倉儲系統的運行效率.

(4) 本文提出的融合框架雖可有效提升智能倉儲系統任務分配的效率, 但仍存在不足.主要是, 成員機器人一次只能執行一個訂單任務、未考慮動態訂單分配等.未來研究將圍繞倉庫動態訂單分配進行, 以不斷接近智能倉儲系統的實際工作情形.