基于Arnold置換的交換加密水印算法①

趙培越, 張珍珍, 丁海洋, 李子臣

(北京印刷學院 信息工程學院, 北京 102600)

1 引言

近年來, 互聯網、云計算、大數據等技術朝著高效快速的方向發展, 數據隱私保護和信息安全[1]日益受到重視, 其中圖像加密和數字水印成為了研究的熱點.在一些特殊領域如醫學、軍事、衛星監測等需要對圖像進行處理, 將密碼技術與數字水印結合到一起,提供了圖像加密與水印共存的安全保護方案[2].

圖像置換作為一種重要的圖像加密和技術, 其目的是將目標圖像進行一定程度上的修改, 使其包含的真實信息可以不被破壞地隱藏起來, 這樣便具有不可見性, 保證了圖像傳輸的安全性.其基本思想是將數字圖像作為矩陣進行有限次的初等置換來使圖像的像素點變得混亂無序, 從而實現加密效果.典型的有幻方置換、騎士巡游置換、Fibonacci置換、基于Hilbert曲線置換[3]等算法.其中Arnold置換直觀、簡單、具有周期性, 使用非常方便, 該方法使像素的移動具有混沌特性, 加密后的圖像安全性較高.

水印算法根據操作域的不同可分為3類: 空域算法、頻域算法以及壓縮域算法.空域算法有基于LSB的水印算法、基于差值擴展的水印算法[4]和基于無損壓縮的水印算法[5]等.其中基于直方圖平移的可逆水印算法[6]是最具代表性的算法之一.文獻[7]對圖像分塊, 建立多個差值直方圖來嵌入水印信息; 文獻[8]通過混沌加密與直方圖平移結合, 實現了無損提取水印信息, 但其水印嵌入容量十分有限; 文獻[9]利用多組差值直方圖平移獲取更多差值, 通過圖像分塊和邊緣差值嵌入, 雖然提高了嵌入率, 但是其含水印圖像質量隨之下降.文獻[10]提出了對載體圖像進行分塊置換加密, 并通過DCT變換來嵌入水印信息, 文獻[11]對水印信息進行置換加密, 對載體圖像進行分塊后過DCT變換與直方圖平移來嵌入水印.

交換加密水印算法是現階段實現密碼技術和水印技術相結合的一種主要方法.文獻[12]最先提出了交換加密水印技術(Commutative Encryption and Watermarking , CEW), 將加解密、水印嵌入、提取融合到一起, 在發送前既可先加密后嵌水印, 也可先嵌水印后加密, 均能得到含水印的密文; 在發送后既可從密文中先提取水印, 再解密恢復圖像, 也可先解密, 再提取水印恢復圖像[13].而置換加密后不會對圖像的某些統計特征造成影響[14], 所以可通過修改原始載體圖像的統計特征來嵌入水印從而實現交換加密水印算法.文獻[15]將原始載體圖像分組嵌入比特信息后, 通過修改數據最低比特, 使得全組數據之和的奇偶性與對應嵌入的水印信息相同, 并在同組數據范圍內進行置換從而實現CEW, 但僅對載體數據進行置亂, 安全性有待提高.文獻[16]通過空間位置置換及修改載體圖像直方圖嵌入水印信息實現CEW.

基于對上述算法的研究, 利用Arnold置換前后直方圖不變的特性, 提出了一種基于Arnold置換的交換加密水印算法.原始載體圖像先進行分塊, 再進行塊內和塊間的置換加密, 通過直方圖平移來實現水印嵌入.加密操作與水印嵌入操作的順序不影響含水印密文的生成, 且解密操作與水印提取操作的順序不影響水印信息的提取與圖像的恢復.實驗結果表明, 該算法可以無損恢復原始載體圖像并提取水印, 且解密后的含水印明文圖像質量高, 水印的不可見性好.

2 基本原理

本節主要介紹Arnold置換, 直方圖平移可逆水印算法及交換加密水印算法.

2.1 Arnold置換

Arnold置換(又稱貓臉置換)是一種基于古典密碼體制的圖像加密算法, 本質上是對長寬相等的圖像中像素點的位置進行多次矩陣運算, 從而改變空間中像素點的位置, 破壞圖像相鄰像素點之間的相關性.

2.1.1 Arnold置換原理

傳統的Arnold置換[3]的矩陣形式可以表達為: 設有平面點集S=[0,1]×[0,1], 對(x,y)∈S則有:

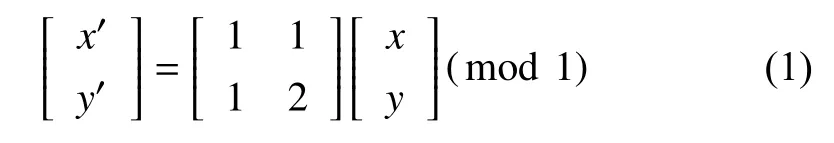
若(x,y)為二維圖像坐標, 那么上述置換可以轉化為:

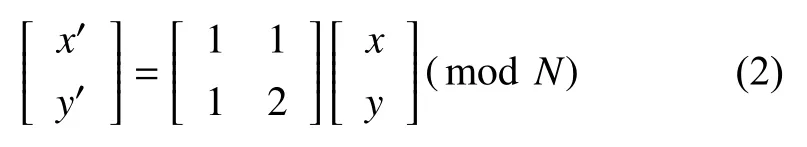
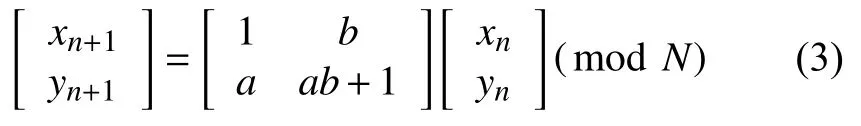
其中,n代表第n次變換.

2.1.2 Arnold置換的周期性

Arnold置換具有周期性[17], 通過對一個4×4矩陣進行Arnold置換來說明Arnold的周期性.

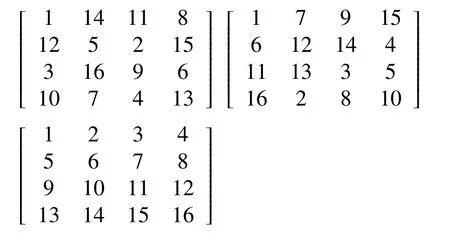
可以看到經過3次置換后, 矩陣A恢復成原始狀態.Arnold置換周期與圖像階數的關系見表1.

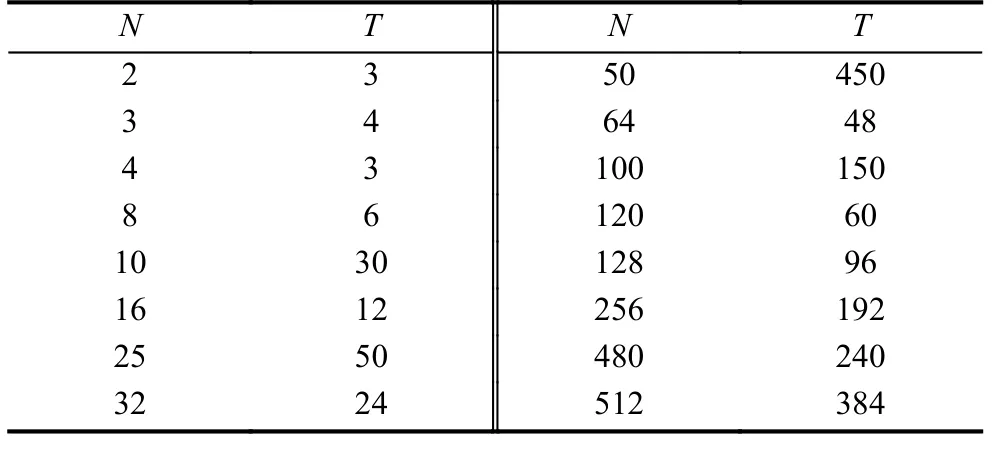
表1 圖像階數N與置換周期T的關系

2.1.3 Arnold置換恢復算法

解密時需要用到Arnold置換恢復算法.目前歸納的Arnold置換恢復算法[18]有3種: 一是利用周期恢復;二是通過逆矩陣恢復; 三是解方程組法.本算法利用周期性來恢復.

設大小為N×N的圖像進行Arnold置換, 置換了n次, Arnold置換周期為T, 以此求恢復圖像.已經置換n次, 利用置換周期, 只要再經過T-(nmodT)次即可恢復原圖.

2.2 基于直方圖平移的可逆水印算法

文獻[19]提出了基于直方圖平移的信息隱藏基本方案, 直方圖中橫坐標是灰度值, 縱坐標是該灰度值對應的像素點的數量, 而每一個豎條稱為一個bin.直方圖中最高的那個點, 就稱為峰點P.最低的那個點(通常為0), 叫做零點Z(如無為0的點, 可以將灰度值為254的點的灰度值改為255, 并進行標記, 以此空出254位置, 最后可根據標記恢復).

對灰度圖像直方圖進行分析, 通過將直方圖峰值點與零點的像素平移來空出嵌入空間, 并在峰值點嵌入水印信息, 提取恢復時根據峰值點與相臨的bin便可提取水印信息并恢復圖像.直方圖平移嵌水印過程如圖1.

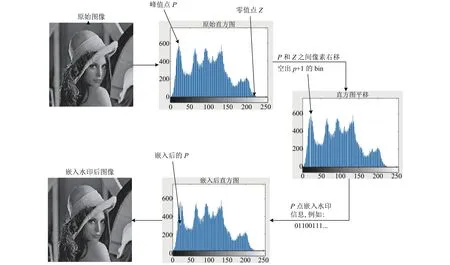
圖1 直方圖平移嵌水印流程圖

2.3 交換加密水印算法

在發送方, 加密與嵌入水印順序可以交換; 在接收方, 可從含水印的密文圖像中直接提取水印, 也可從解密后恢復圖像的中提取水印, 從而達到交換加密水印的目的.交換加密水印算法框架如圖2.其中I為原始載體圖像,w為水印,k為密鑰,Iw為含水印圖像,為含水印密文圖像.

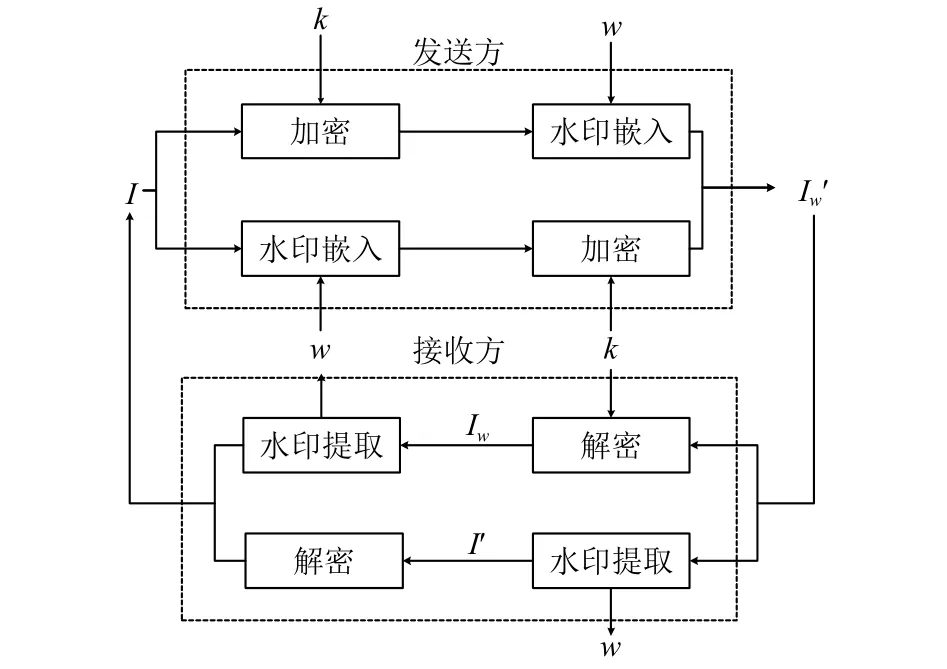
圖2 交換加密水印算法框架

3 基于Arnold置換的交換加密水印算法

本文提出的基于Arnold置換的交換加密水印算法如圖3.

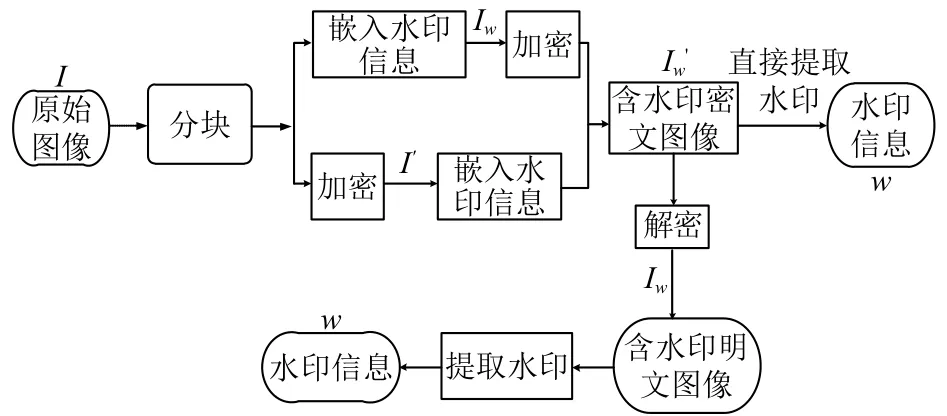
圖3 基于Arnold置換的交換加密水印算法

算法步驟可總結如下:

(1) 對原始圖像進行分塊;

(2) 在嵌入水印時, 在明文和密文中均可以嵌入,最終得到含水印密文圖像;

(3) 提取水印時, 可從含水印密文圖像中直接提取,也可解密后再提取.

3.1 含水印密文圖像的生成

算法中涉及的參數有a、b、n1、n2、T1、T2.其中a、b為置換矩陣參數,ab≠0, (n1modT1)≠0,(n2modT2)≠0.n1為水印圖像置換次數與原始圖像各小塊的塊間置換次數,n2為原始圖像各小塊的塊內置換次數.T1為水印圖像對應的置換周期,T2為原始圖像小塊對應的置換周期.

3.1.1 先加密后嵌水印

其步驟可總結如下:

(1) 水印圖像m置換n1次, 得到水印w;

(2) 把原始圖像I分為k個的大小為8×8的明文分塊, 記第k小塊為I(k).對I(k)按照2.1.1小節分別進行塊內置換n2次、塊間置換n1 次, 最終得到密文圖像I′;

(3) 按照從上到下、從左到右的方式遍歷密文小塊I′(k)的像素點;

(4) 將小塊內P+1到Z-1的所有bin向右平移一位, 空出P+1的bin.可通過判斷某個點的灰度值是否在P-Z之間, 然后對應灰度值加1即可;

(5) 每個密文小塊嵌入1 bit信息, 嵌入到峰值點P中.僅在第一個峰值點像素值P處嵌入信息.嵌0就是加0運算, 嵌1就是加1運算, 這樣像素值就會保持為P不變或者變為P+1.

嵌入公式如式(4)所示:

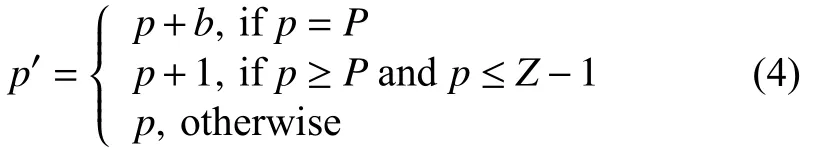
其中,p是原始像素值,b是1 bit水印,p′是嵌入信息后的像素值;

(6)將全部水印信息嵌入到密文圖像I′, 最終得到含水印的密文圖像.

3.1.2 先嵌水印后加密

其步驟可總結如下:

(1) 水印圖像m置換n1次, 得到水印w;

(2) 把原始圖像I分為k個的大小為8×8的明文分塊, 記第k個小塊為I(k);

(3) 按照3.1.1小節中步驟(3)-步驟(5), 將水印w嵌入到原始圖像I中, 每個小塊嵌入1 bit信息, 最終得到含水印的圖像Iw;

(4) 對Iw按照式(3)分別進行塊內置換n2次、塊間置換n1次, 最終得到含水印的密文圖像.

3.2 水印提取與圖像恢復

接收方接收到含水印的密文圖像后進行相應處理,可先提取水印信息、恢復圖像; 也可解密以后再提取水印信息、恢復圖像.在提取水印時, 因為每個小塊只嵌入1 bit水印信息, 所以只需判斷像素值為P+1的點的個數即可得知該小塊嵌入的是0還是1.

本文以先加密后嵌水印得到的含水印密文圖像為例, 對提取水印恢復圖像過程進行詳細描述.

3.2.1 直接提取水印、恢復圖像

其步驟可總結如下:

(1) 按照與嵌入時相同的方式遍歷小塊Iw′(k)的像素點.

(2) 判斷小塊Iw′(k)內像素值P+1的個數num.

(3) 提取1 bit水印信息, 如式(5)所示:

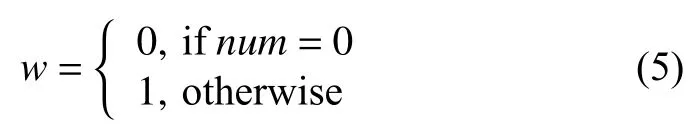
(4) 其他小塊重復步驟(1)-步驟(3), 完成全部水印信息的提取, 最終得到水印圖像w, 然后對w再置換T1-(n1modT1)次得到水印圖像m.

(5) 提取水印后, 將I′(k)中像素值進行處理, 如式(6)所示:

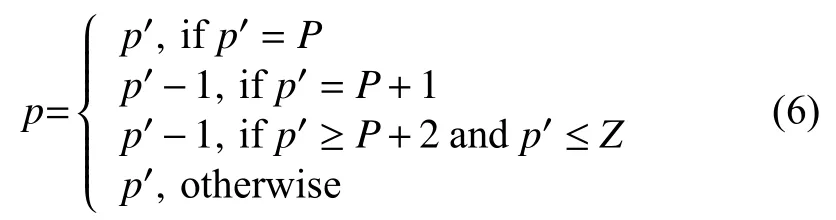
(6) 其他小塊重復步驟(1)-步驟(5), 最終獲取完整的密文圖像I′.

(7) 對I′(k)塊間置換T1-(n1modT1)次, 塊內置換T2-(n2modT2)次, 得到恢復圖像.

3.2.2 先解密, 再提取水印恢復圖像

其步驟可總結如下:

(2) 對Im各小塊進行處理, 同3.2.1小節中步驟(1)-步驟(3).最終得到水印m.

(3) 按照式(6)對提取水印后的圖像進行處理, 得到恢復圖像.

4 算法仿真分析

本文算法在Matlab R2020a, Windows 10操作系統下進行仿真測試, 使用水印算法的客觀評價標準, 選取大小為512×512的經典灰度圖像進行測試, 從加密參數、不可見性、可逆性、效率說明算法的性能.置換矩陣中參數選取為a=1,b=1.

4.1 加密參數測試

嵌入率可以用來衡量算法的嵌入容量, 計算公式如式(7)所示:

選取三幅灰度圖Lena、Boat、Peppers, 在嵌入水印容量為0.156 bpp時, 對置換加密參數(n1,n2)進行測試.選取6對不同參數對 (n1,n2)時, 在密文域嵌水印,解密后得到的含水印圖像的PSNR值見表2.

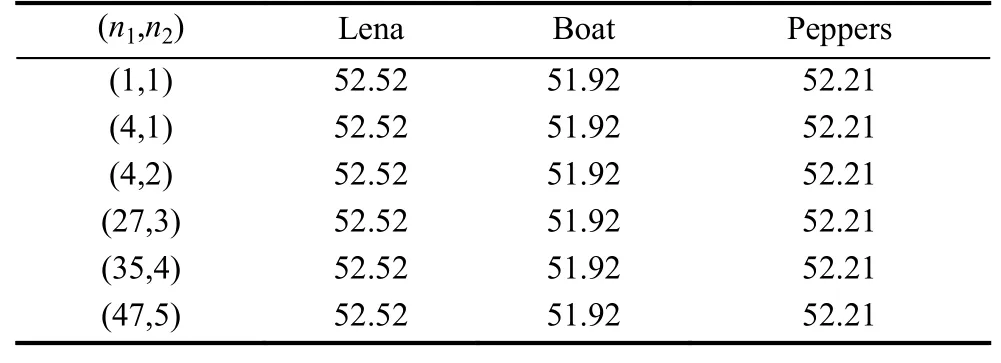
表2 不同(n1, n2)時含水印圖像PSNR值 (dB)

4.2 不可見性測試

峰值信噪比PSNR值可以說明含水印明文圖像中水印的不可見性, PSNR值越大, 說明水印的不可見性越好.本文算法在不同嵌入容量下, 解密得到的含水印圖像的PSNR值及平均PSNR值.見表3.

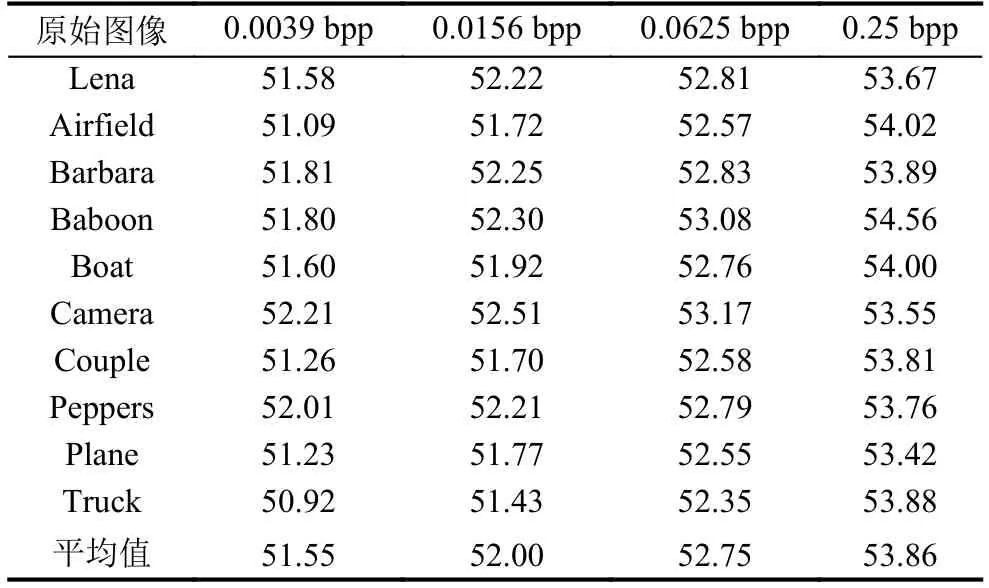
表3 不同嵌入容量下PSNR值及平均值 (dB)

通過表3不難看出, 本文算法在水印嵌入后, PSNR平均值都在51 dB以上, 且隨著嵌入容量的增加, PSNR值有所提升.

嵌入率為0.0156 bpp, 載體圖像為Lena圖時在密文中嵌水印實驗結果, 如圖4.

嵌入率為0.0156 bpp, 載體圖像為Lena圖時在明文中嵌水印實驗結果, 如圖5.

通過圖4和圖5可以看出在密文域或明文域中嵌水印, 解密后含水印圖像質量較高, 水印不可見性好.

圖4 密文域嵌水印實驗結果

圖5 明文嵌水印實驗結果

本文還與文獻[7-9]中相關經典算法進行對比, 見表4.

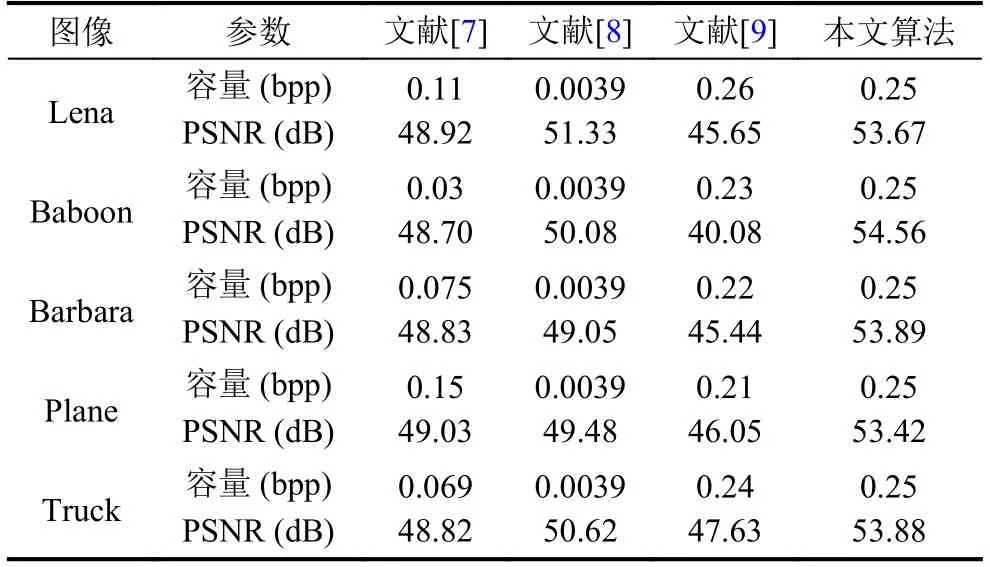
表4 算法性能對比

與文獻[7]、文獻[8]算法對比, 可以看出本文算法在PSNR值與嵌入容量上占優; 與文獻[9]對比, 在嵌入容量相近時, 本文算法PSNR值也要更高.

4.3 可逆性測試

通過歸一化系數NC值來判斷是否有可逆性.本文給出了10幅512×512大小的灰度圖像的NC值, 見表5.

從表5中可以看出, 所有圖像的NC值均為1, 說明恢復圖像與原始圖像一樣.而且提取出的水印錯誤率為0, 說明本算法具有可逆性.

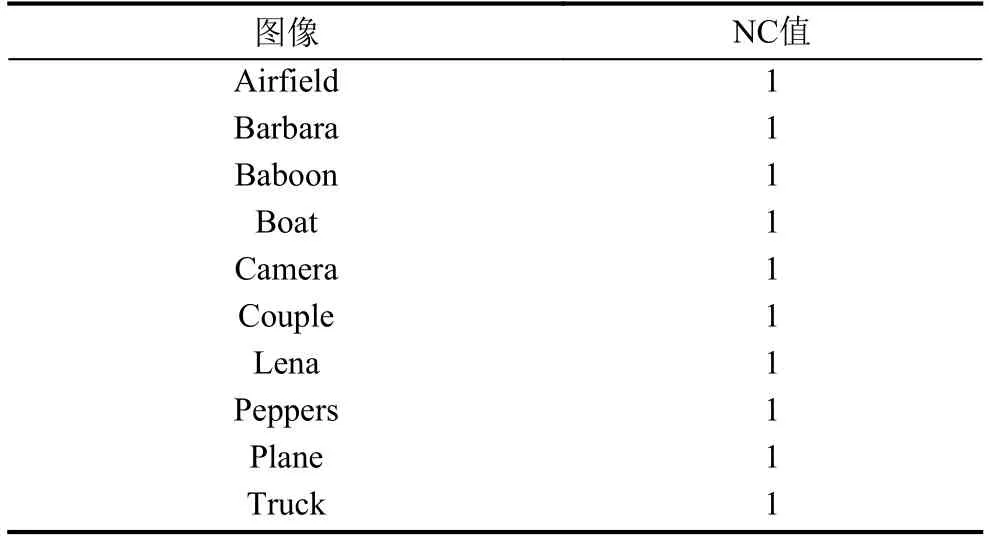
表5 可逆性測試

4.4 算法效率測試

本實驗還進行了算法效率測試, 在不同嵌入容量下, 對10幅灰度圖分別進行10次測試, 最后取平均值,結果見表6.

表6 不同嵌入容量下各算法的運行時間(s)

由表6可知, 隨著數據量的增大, 算法所需時間有所增長, 但總體滿足效率要求.

5 結束語

本文提出的基于Arnold置換的交換加密水印算法, 實現了加密操作與水印操作的交換, 解密后的含水印圖像質量高, 水印的不可見性好.算法中兩次置換加密提高了載體圖像在使用及分發時的安全性, 不僅能有效保護與恢復載體圖像, 而且從含水印密文圖像或解密后的含水印圖像中都能提取水印信息, 對于身份認證與版權保護有著重要作用, 可以廣泛地應用于醫學、軍事等領域.