基于高階組合能量算子的滾動軸承故障診斷*

陳霽恒 朱丹宸 譚經松

（海軍士官學校 蚌埠 233000）

1 引言

滾動軸承作為旋轉機械的關鍵零部件得到了廣泛的使用，然而，由于其常工作在高溫、高速和重載等惡劣環境中，導致故障時有發生，極大地影響著整個設備的使用性能和安全運行，因此，開展針對滾動軸承的狀態監測和故障診斷就顯得尤為重要。而目前，受到測量手段的限制，在結構較為復雜的設備中，滾動軸承和信號測量所用傳感器之間常存在較為復雜的傳遞路徑，導致較強的信號能量衰減，致使測得的信號中故障特征微弱，且伴隨著強背景噪聲，給準確的滾動軸承故障特征提取帶來較大的困難。就運行狀況來看，滾動軸承常工作在時變轉速工況下，導致故障產生的沖擊信號失去了周期性特征，故障特征頻率隨著時間不斷變化，信號存在強烈的非平穩特性，此外，許多經典的信號處理方法無法直接應用于變轉速工況下的滾動軸承故障特征提取。

近年來，變轉速工況下的滾動軸承故障診斷得到了廣泛的研究，且取得了不少成果，其中，階次跟蹤作為最常見的方法之一［1～2］，被用于消除轉速波動帶來的影響。階次跟蹤的核心是通過角域重采樣將非平穩的時域信號轉換成平穩的角域信號，然而經典的階次跟蹤方法依賴于編碼器或者轉速計以提供軸承的瞬時轉頻、相位作為參考，易受到測試條件的限制。因此，許多學者研究利用短時傅立葉變換（Short Time Fourier Transform，STFT）等時頻分析方法，提取出信號中的瞬時轉頻信息，實現了無轉速信號的階次跟蹤［3～6］。然而，該方法計算結果的準確性和有效性受到計算過程的制約，如Vold-Kalman濾波常被用于提取時頻圖中的某一階瞬時頻率，然而，求解過程中包含大型稀疏矩陣求逆，極大地增加了計算的復雜度，降低了計算效率。除此以外，為了避免重采樣過程產生的誤差，也可以通過提取時頻圖中瞬時故障特征頻率和瞬時轉頻曲線，利用兩者間的瞬時比值確定軸承的故障類型。考慮到軸承故障信號中的強背景噪聲干擾，一些常見的信號分析方法也被用于提高信號的信噪比，如 EWT［7］、EMD［8］、AR 模型［9］等，進一步提高了故障特征提取的有效性。

在實際測量過程中，系統中的齒輪嚙合，不平衡、不對中故障，轉頻調制等現象均會導致振動信號中存在明顯的轉頻成分，且不易受高頻噪聲的干擾；然而，復雜傳遞路徑會導致微弱的故障特征被背景噪聲所淹沒，不利于瞬時故障特征頻率曲線的準確提取。基于此，為了方便實際使用，本文提出了一種無需轉速信號的變轉速工況下滾動軸承故障特征提取方法，首先，利用STFT和短時Chirplet-Fourier變換對滾動軸承故障信號進行時頻表示，為了減小計算誤差，提取出時頻圖中多階明顯的轉頻分量，通過算術平均的方法得到最終的瞬時轉頻曲線，并基于此實現時域非平穩信號的角域重采樣；為了提高重采樣信號的信噪比，提出基于改進高階組合能量算子的沖擊特征增強方法；最后，通過FFT得到的階次譜實現了滾動軸承故障特征的有效提取。

2 改進高階組合能量算子的基本原理

2.1 高階能量算子的原理

高階能量算子在計算過程中，只需要知道信號的幅值和導數，計算的復雜性較低，效率較高，對信號的瞬態變化較為敏感，能夠準確估計信號的瞬時幅值包絡和瞬時頻率。

對于連續信號x（t），其高階能量算子表示為［10］

式（1）中，k為能量算子的階數，x（k-1）和 x（k）分別表示信號的k-1階和k階導數。

對于離散時間信號x（n），其高階能量算子可以表示為［11］

分析式（1）和式（2）可知，當階數k=2時，高階能量算子即為最常用的Teager能量算子。相比于Teager能量算子，高階能量算子進一步增強信號中的瞬態成分，因此，可將高階能量算子用于提取滾動軸承故障沖擊特征。但由于高階能量算子在計算時使用了差分算子，在增強沖擊成分的同時，也會增強信號中的高頻噪聲成分，由此，選取合適的階數就顯得尤為重要。

2.2 高階組合能量算子的構造方法

為了充分發揮高階能量算子的解調能力，最大限度的提取原始振動信號的沖擊成分并減小噪聲成分的干擾，考慮到2～j階能量算子的結果中，可能存在噪聲干擾較為嚴重，特征提取效果不佳的分量。基于此，本文提出了一種新的高階組合高階能量算子，具體的構造方法如下。

1）確定能量算子的最大階數K，為了提高計算效率，K值不宜取過大，本文將K設定為20；

2）為了提高分析效果，對2～K階能量算子進行預先篩選，去除其中沖擊特征不明顯的階數，本文提出利用高階能量譜峭度作為指標。首先，設離散時間信號x（n），其長度范圍為1～N，采樣頻率為fs，對第k階能量算子進行快速傅里葉變換得：

式（3）中，ES（n）表示頻率范圍為0～fs/2范圍內的高階能量譜值。其次，峭度可以衡量信號中明顯的峰值和沖擊成分，假設ES（n）的均值為μES，則高階能量譜峭度可以定義為

對于高階能量譜來說，如果高階能量算子的結果中包含明顯的故障沖擊成分，則在能量譜中，故障特征頻率處表現為明顯的峰值，會導致峭度值的增加，因此，以高階能量譜峭度為指標可以選取出高階能量算子中故障特征較為明顯的階數，本文將選取的數量設定為6；

3）假設選取出的6階能量算子的階數分別為k1、k2、k3、k4、k5和 k6，則信號 x（n）的高階組合能量算子可以表示為

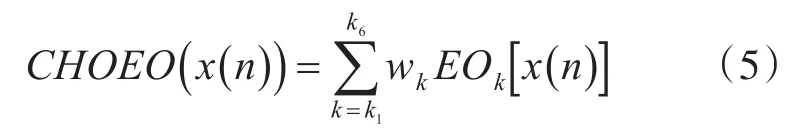
式（5）中，wk表示第k階能量算子對應的加權系數，本文設定其取值范圍確定為0～1。

2.3 加權系數的優化選取策略

從式（5）可以看出，需要對加權系數wk進行優化選取以保證高階組合能量算子的分析結果。粒子群算法（PSO）作為一種常見的優化算法由于其較好的尋優能力得到了廣泛使用。假設PSO的種群數量為N，搜索空間的維度為D，則對于空間中的任意一個粒子i，其位置和速度向量可分別表示為為粒子 i的最佳位置可以利用一個向量進行表示，Pbest=，整個種群的最佳位置可以表示為粒子i的位置和速度需要進行隨機初始化，且按照一定公式的進行調整更新：

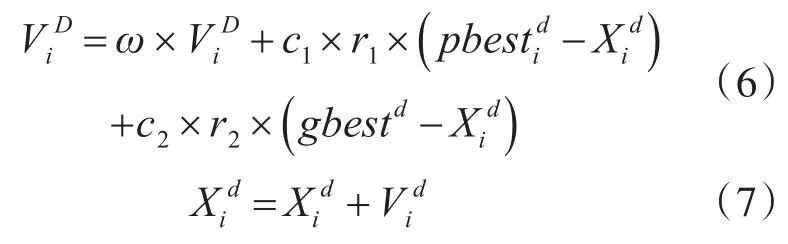
由于在經典的粒子群優化中，尋優過程缺乏多樣性，導致搜索結果容易出現局部最優解，并提前收斂。為了解決這些問題，本文選取了一種改進的粒子群算法［12］。

由于信息熵可以衡量信號中的不確定度，表征信號中隨機噪聲的含量，對于軸承故障信號而言，越小的信息熵值表示信號中的隨機噪聲干擾越小，故障特征越明顯，因此，本文將熵作為優化過程中的適應度值，且最小熵所對應的粒子位置即是所需的最優解。對于離散時間信號x（n），假設其fourier變換結果為X（ω），則其能量譜可以定義為

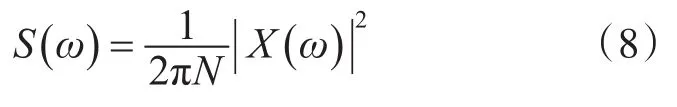
那么，歸一化的信息熵可以定義為［13］

式（10）中，Si表示能量譜中的第i個值。

3 瞬時轉速估計方法

短時Chirp-Fourier變換作為一種類似于STFT的時頻表示方法，具有時頻聚焦特性，可以使分析得到的時頻圖中瞬時轉頻的脊線更加清晰，其數學表達式為［3］

式（11）中，ωT0表示中心時刻為τ=0長度為T0的窗。短時Chirp-Fourier變換不再受到信號需要局部平穩的條件限制，而是通過中心頻率為fτ，調制頻率為c的基函數對任意時刻信號的時頻特征進行匹配，從而實現信號的分段逼近，STFT是c=0的特殊情況。

由此，更為清晰的瞬時轉頻曲線可通過在局部范圍內取最大值的方式獲得［14］：

由此，本文提取瞬時轉速的過程可以總結為如下。

1）基于STFT、式（12）和（13）對轉頻進行初步估計，選取了N個明顯的諧波分量，記為Fkn(t)；

2）依據中心差分法，分別對各階諧波分量的瞬時調頻值進行計算［3］：

3）式（14）中，ti為第i個窗的中心時刻，ckn(ti)表示第i個窗內第kn階諧波分量的調頻估計值；

4）將ckn(ti)帶入式（11），對原始信號進行短時Chirp-Fourier變換，分別得到N個脊線更為清晰的時頻表示圖；

5）提取出第kn階諧波表示的瞬時頻率值，記為fkn(t)，則最終提取得到的瞬時轉頻為

問卷調查盡量以隨機抽樣為主，所以調查時采用簡單隨機抽樣來計算大學生群體的樣本量，其計算公式為，其中：為總體總量；為一定置信水平下對應的標準正態臨界值；為抽樣概率；為抽樣極限誤差.

4 故障特征提取流程

本文考慮到滾動軸承工作在變轉速工況下的特點，結合強背景噪聲干擾的實際，提出基于改進高階組合能量算子的變轉速工況下滾動軸承弱故障特征提取方法。算法的流程如圖1所示，具體過程如下。

圖1 本文算法流程

1）采集滾動軸承在變轉速工況下的振動信號，基于短時Chirp-Fourier變換計算瞬時轉頻曲線；

2）基于步驟1）得到的轉頻曲線，將時域信號轉換成角域信號；

3）基于角域信號，構造高階組合能量算子，利用改進的粒子群算法對加權系數進行優化選取并得到改進組合高階能量算子的結果；

4）利用FFT處理步驟4）的結果，獲得最終的階次譜。

5）在變轉速工況下，需要通過提取故障特征階次來判斷滾動軸承故障類型。滾動軸承內圈、外圈故障特征階次Oi和Oo可分別表示為

式（16）中，d為滾動體的直徑，D為節徑，Z為滾動體的個數，α為接觸角。由此，通過觀察步驟5）得到的階次譜中幅值對應的階次，并與理論故障特征階次相比較，就可以判斷滾動軸承故障類型。

5 仿真信號分析

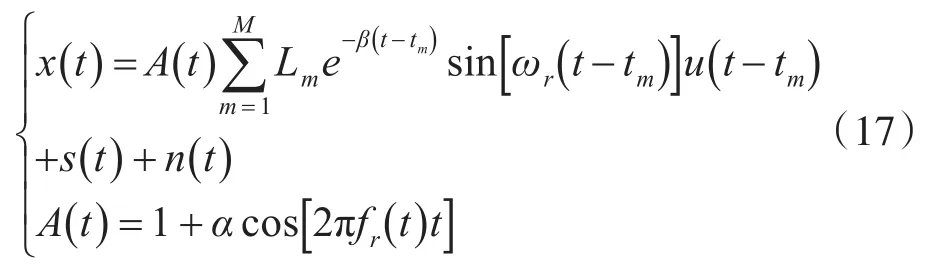
式（17）中，A（t）表示與轉頻fr（t）相關的幅值調制，α＞0為一個常數；u（t-tm）表示階躍函數，當t＞tm時，u=1，當t＜tm時，u=0；Lm=L0+ηfr（tm）表示與fr（t）相關的幅值，L0和η均為常數，tm為第m個故障沖擊的時間；s（t）和n（t）分別表示信號 x（t）中的正弦諧波分量和噪聲干擾成分。每個故障沖擊的時間tm可以通過下式進行計算［15］：

式（18）中，μ表示滾動體的滑移率，fc（t）表示瞬時故障特征頻率。諧波分量s（t）可以表示為

式（19）中，Ns為諧波數量，Bi為第i個諧波成分的幅值。仿真信號的具體參數見表1。將隨機噪聲的大小確定為-10db，假設fc（t）=5.5fr（t），即故障特征階次為5.5。仿真信號的采樣頻率為20000Hz，仿真時長為2.5s。

表1 仿真信號參數

利用本文提出的算法分析該仿真信號，首先，基于短時Chirp-Fourier變換對原始仿真信號進行時頻表示，結果如圖2（a）所示，圖中僅能識別出一階轉頻曲線，所以瞬時轉速計算過程中僅利用該階分量。提取得到的瞬時轉速如圖2（b）所示，圖中藍色實線表示計算得到的瞬時轉頻，紅色實線表示理論上的真實轉頻，通過對比可知，兩者之間的差距較小，說明對于該仿真模型，瞬時轉頻分量得到了有效提取。

圖2 瞬時轉速計算

接下來，以計算得到的瞬時轉速為基礎，通過三次樣條插值，對原始仿真信號進行角域重采樣，原始時域信號和重采樣得到的角域信號分別如圖3（a）和（b）所示。

圖3 仿真信號的波形圖

利用2～20階能量算子處理圖2（b）所示的角域信號，通過比較各階能量算子的能量譜峭度值，選取第7、5、2、17、12、10階能量算子（以能量譜峭度值從大到小進行排序）構造改進高階組合高階能量算子，使用優化算法時的種群個數和最大迭代數分別設定為100和300，結果如圖4所示。圖4（a）為優化時的收斂曲線，從圖中能夠看出，當迭代次數為222時，適應度函數取到最小值0.6238，此時對應的粒子位置為［0.5115，0.0112，0.9903，0.4436，0.3986，0.0236］，將此時的粒子位置作為高階組合能量算子的最優加權系數，得到的最優組合能量算子結果如圖4（b）所示，通過FFT可以得到最終的階次譜如圖4（c）所示，圖中展示的最大階數為30。階次譜中1階及2階轉頻較為明顯，在階次5.45（與理論值故障特征階次5.5接近，滑移率的存在導致了兩者間的誤差）及其諧波成分10.9和16.35處出現明顯的峰值，圍繞故障特征階次及其諧波成分，間隔為轉頻的調制邊頻帶也能夠得到識別，以上特征符合仿真模型的設置，可以判斷該滾動軸承存在內圈故障。

圖4 本文算法處理仿真信號的結果

作為對比，本文利用EMD［8］處理圖3（b）所示角域信號，分別計算分解得到的14個IMF的峭度值及其與原始信號的相關系數ρ，作為選取有效IMF的依據。將有效分量ρ的閾值設定為0.1。圖5（a）展示了分解得到的前4階IMF，通過計算，第1、2、3、4、5和7階IMF的相關系數大于0.1，值分別為0.77、0.46、0.24、0.17、0.14、0.18，這6階IMF的峭度值分別為 3.26、3.08、2.84、2.81、2.93、2.32。由于IMF1的峭度值最大，所以對IMF1進行包絡分析，結果如圖5（b）所示。包絡譜中僅能明顯識別出轉頻成分，故障特征階次5.45及其調制邊頻帶，且各特征的幅值明顯小于圖4（c）中的幅值，通過比較，本文提出的方法可以在噪聲的干擾下，提取出更為豐富和明顯的故障信息，體現出方法的有效性。

圖5 EMD方法處理角域信號的結果

6 實驗數據驗證

本節使用試驗臺測得的滾動軸承故障信號進行進一步分析，試驗臺的具體結構如圖6所示。實驗過程中將測點選在靠近支撐結構的基座上，測量垂直于臺面方向的振動。由于測點遠離故障點，復雜的傳遞路徑使實測信號包含了更多的干擾成分，增大了故障特征提取的難度。為了模擬滾動軸承在變轉速工況下運行，實驗時的平均轉速為3000r/min并以300r/min上下做正弦波動，受到轉速波動的影響，進一步加大了實測振動信號的復雜性，增大了故障特征提取的難度。

圖6 試驗臺

實驗所用軸承為NSK7010c，其結構參數見表2，信號采集時的采樣頻率設定為32768Hz，采集時長為2s，通過計算可知該軸承的外圈故障特征階次為8.27。實測信號的時域波形如圖7（a）所示，受到轉速波動以及背景噪聲的干擾，時域圖中無法識別軸承故障導致的沖擊成分。理論上，軸承外圈故障信號中不應該包含轉頻信息，然而，由于該故障模擬平臺同時存在不平衡故障，導致采集得到的振動信號中包含轉頻信息，由此，依舊可以使用本文提出的算法分析實測信號。

表2 測試軸承參數

圖7 實驗信號及其時頻表示

圖7（b）為利用STFT分析原始振動信號的結果，時頻圖中可以識別出1至5階轉頻分量，通過計算可知，利用時頻圖中第3階和第5階轉頻曲線，可以有效提取瞬時轉頻，結果如圖8所示。圖8（a）為提取第3階轉頻成分時，通過短時Chirp-Fourier變換得到的時頻圖，對比圖7（b）中的第3階轉頻，圖8（a）中的第3階轉頻曲線更為明顯和聚集，有利于轉頻的提取，提取結果如圖8（b）所示。同理，圖8（c）為提取第5階轉頻成分的時頻圖，提取得到的瞬時轉頻如圖8（d）所示。

圖8 瞬時轉速計算結果

為了減小隨機誤差，對提取得到的兩階轉頻曲線進行平均，圖9的平均轉頻曲線大致在45Hz和55Hz之間做正弦波動，這與設定的轉頻波動方式是一致的。下面利用該平均轉頻曲線進行角域重采樣，得到的結果如圖10（a）所示。通過計算2～20階能量算子的能量譜峭度值，選取17、15、19、14、4和16階能量算子構造高階組合能量算子進行后續分析。

圖9 3階和5階轉頻曲線的平均值

通過優化算法對構造的高階能量算子的加權系數進行優化選取，優化過程的收斂曲線如圖10（b）所示。根據收斂曲線，當迭代次數為117次時，可以取到最小適應度值0.7911，此時對應的粒子位置為［0.053，0.539，0.867，0.668，0.353，0.001］，將該粒子位置作為最優加權系數進行高階組合能量算子的計算，結果如圖10（c），利用FFT分析該高階組合能量算子，最終的階次譜如圖10（d）所示，圖中階次為8.3處的譜線幅值較為突出（與外圈故障特征階次的理論值相接近），同時其2～6階諧波成分階處的幅值也較為明顯，背景噪聲雖然存在但干擾較小，滾動軸承的外圈故障特征得到了準確提取，證明了本文提出方法的有效性。

圖10 本文算法分析實驗信號的結果

與仿真分析類似，利用EMD處理重采樣得到的角域信號，減小噪聲的干擾，提取故障特征成分，結果如圖11所示。EMD分解共得到了16個IMF，圖11（a）展示了其中的前4階，分別計算各階IMF與原始信號的相關系數，僅有前4階IMF的ρ＞0.1，分別為0.783、0.526、0.291和0.134。前4階IMF的峭度值分別為2.446、2.641、2.73和2.851，選取峭度值最大的IMF4進行包絡分析，得到的包絡譜如圖11（b）。包絡譜中僅有8.3階處的幅值較為突出，與外圈故障特征階次相對應，然而其諧波成分未得到有效提取，分析效果欠佳。通過對比，進一步驗證了本文算法在變轉速工況下，從強背景噪聲干擾中提取弱故障沖擊特征的能力。

圖11 EMD分析實驗信號的結果

7 結語

滾動軸承在實際工作過程中常處于轉速波動或是升、降速的工況下，從而導致許多經典的故障診斷方法失效，結合復雜傳遞路徑影響下，故障產生的沖擊成分較為微弱常被背景噪聲所淹沒的特點，提出基于改進高階組合能量算子的變轉速工況下滾動軸承弱故障特征提取方法，本文的研究結果表明。

1）利用原始振動信號的時頻圖進行瞬時頻率的估計，并基于此實現時域信號的角域重采樣，可以消除轉速波動的影響，避免了對于轉速信號的依賴，計算過程較為簡便，具有良好的適用性。

2）基于高階能量算子能夠增強信號中沖擊成分的特點，提出了改進高階組合能量算子的構造方法，并將其運用于增強滾動軸承的故障特征，能夠實現比單一階數能量算子更好的效果；

3）仿真和實測信號的分析結果表明，本文提出的方法能夠在轉速波動和強背景噪聲的影響下，準確提取出滾動軸承故障特征，且與基于EMD的包絡階次方法相比，本文方法提取出的故障信號更為豐富，診斷效果更佳，具有更強的工程實踐應用價值。