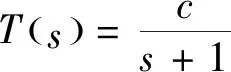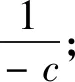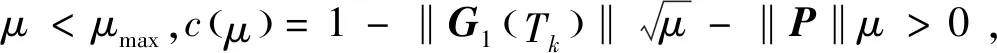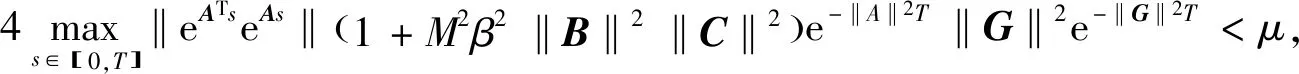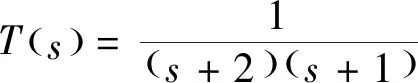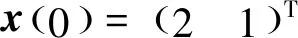具有第二類脈沖寬度調制隨機系統的穩定性分析
蘭德新,葉麗霞
(武夷學院數學與計算機學院,中國 武夷山 354300)
近年來,脈沖寬度調制被廣泛地應用于電流控制、信號處理及神經網絡等系統的許多領域中[1-7]。尤其是加入隨機干擾的脈沖寬度調制反饋系統穩定性的研究,已受到許多學者的關注,文獻[8-15]詳細介紹脈沖寬度調制反饋系統穩定性理論的相關研究結果。文獻[9]利用李雅普諾夫函數、隨機分析法和廣義積分算子不等式,研究了具有馬爾科夫切換和時滯的隨機微分方程的p方指數穩定性問題,文獻[12]利用李雅普諾夫函數和伊藤積分,研究了一類具有第一類脈沖寬度調制的隨機系統的全局指數穩定性問題并取得相關結果。目前,對于脈沖寬度調制反饋系統的穩定性研究大多涉及第一類脈沖寬度調制,對第二類脈沖寬度調制反饋系統研究的比較少。在文獻[14]中,作者研究第二類脈沖寬度調制反饋系統的穩定性,并建立相應的理論結果,其結果顯示第二類脈沖寬度調制反饋系統趨于平衡點的速度快于具有第一類脈沖寬度調制的反饋系統。
本文在文獻[14]的基礎上,加入隨機干擾,利用李雅普諾夫函數,線性矩陣不等式和伊藤積分法,研究了具有第二類脈沖寬度調制的隨機系統的p方指數穩定性問題,給出這類系統p方指數穩定性的充分條件,并通過合理選擇脈沖寬度調制參數的最大上界,使該系統達到穩定。同時用兩個具體實例說明這類系統具有更強的抗干擾能力且趨于平衡點的速度快于具有第一類脈沖寬度調制的隨機系統。
1 預備知識
令(Ω,F,P)表示一概率空間,Rn表示n維歐氏空間,對?x∈Rn,定義x∈Rn:Ω→X?Rn上的可測函數。令I表示一指標集,對?t∈I,定義X(t)為(Ω,F,P)上的隨機變量,則{x(t),t∈I}表示一隨機過程。
考慮如下的隨機系統,其流程如圖1所示。
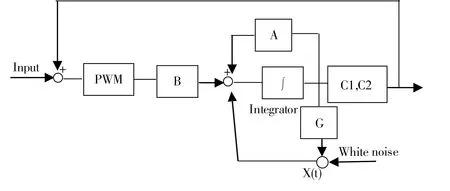
圖1 隨機系統的流程圖Fig. 1 Block diagram of stochastic systems
定義隨機系統的第二類脈沖寬度調制的輸出函數為
(1)
其中e(t)=r(t)-y(t),r(t)表示激勵輸入,y(t) 表示系統輸出,k=1,2,…,Tk表示脈沖寬度,sgn表示符號函數。定義脈沖寬度Tk和符號函數sgn為
(2)
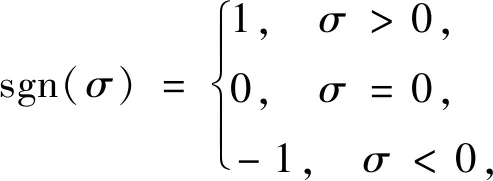
其中T為樣本周期,M為脈沖的振幅,β為常數,若Tk不存在,則令Tk=T。
本文總假設r(t)≡0,記第二類脈沖寬度調制的脈沖寬度Tk在采樣時刻kT取決于錯誤信號:
則具有第二類脈沖寬度調制的隨機系統被描述為
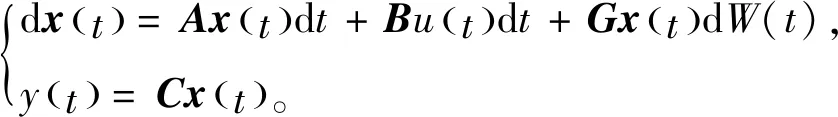
(3)
其中x∈Rn,y∈R,u∈R表示脈沖寬度調制的輸出,A,B,C和G表示相同維數的矩陣,W(t)表示維納過程。注意到x(t)=0是隨機系統(3)的一個平衡點。
下面給出相關的定義和引理。
定義1[12]設{T,X,A,S}為一隨機動力系統,記d是域X上的測度,M?A,t0∈T,a是初始狀態,
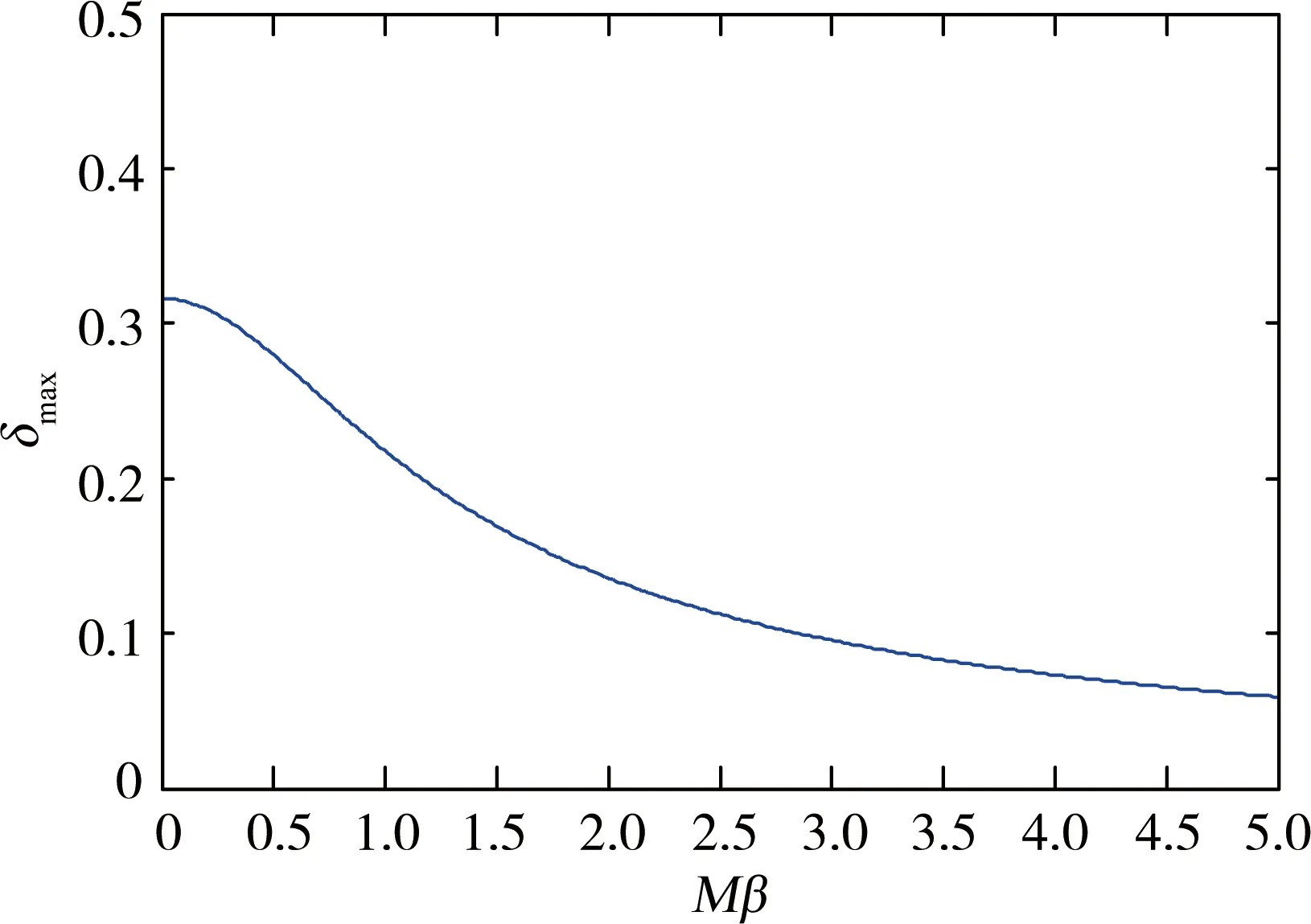
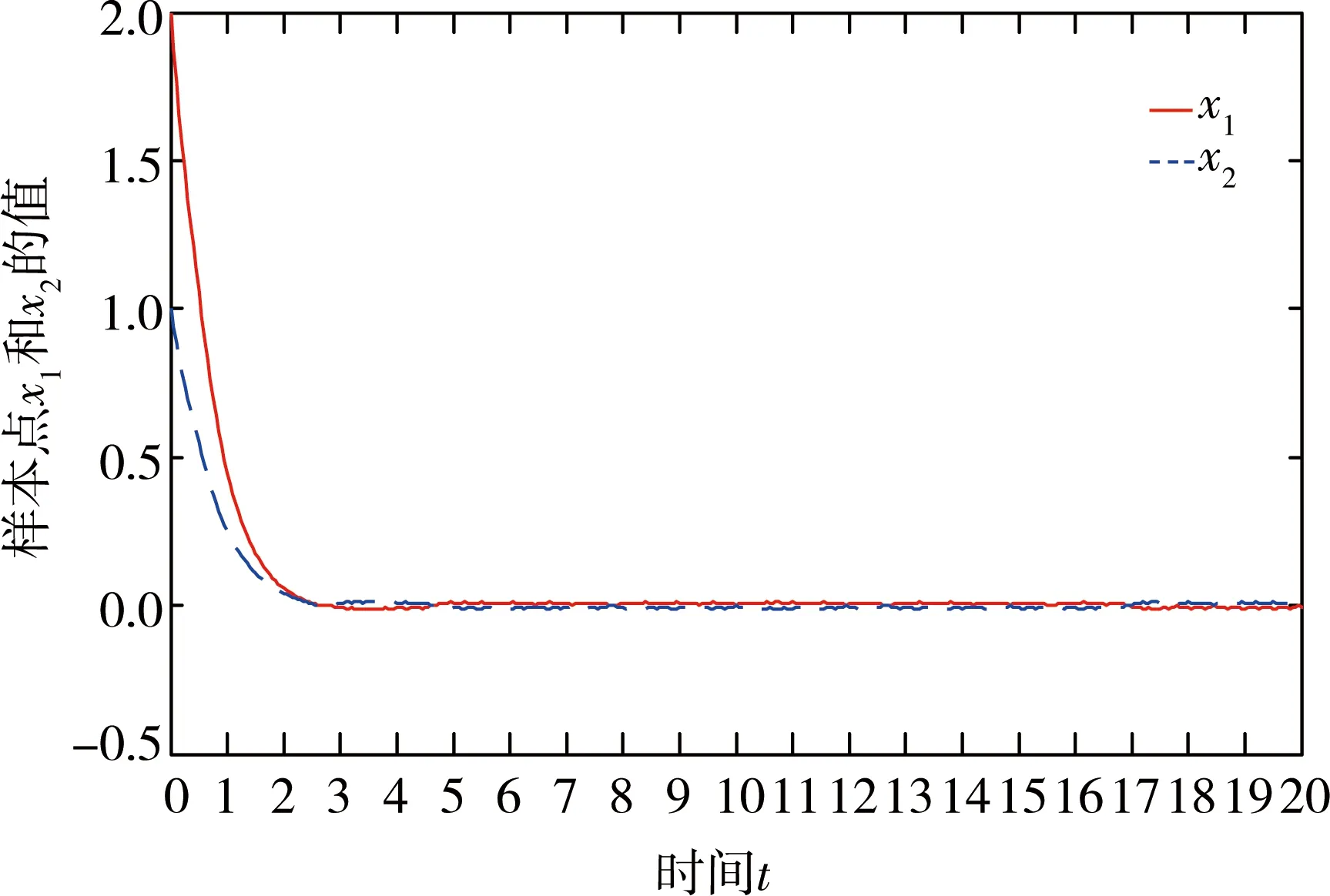
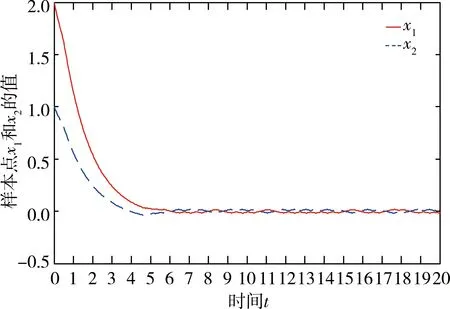
(1)如果對?ε>0,?δ=δ(t0,ε)和常數β>0,k>1,使得當d(a,M)<δ時,對?x(·,·,a,t0)∈S都有E[d(x(t,ω,a,t0),M)p] (2)如果上述δ不依賴于t0,則稱(S,M)是p方一致指數穩定的; (3)如果對?ε>0,?δ=δ(ε)>0,τ=τ(ε),使得對?x(·,·,a,t0)∈S,?t>t0+τ,當d(a,M)<δ時,有E[d(x(t,ω,a,t0),M)p] 引理1[13]假設W(t)是一維納過程。如果φ(t,ω)是有界的初等函數,則 (4) 定理1 假設隨機系統(3)中的矩陣A是赫茲穩定的,且滿足下列條件: (1)-MβCB<1; 則隨機系統(3)在平衡點xe=0處達到p(p∈Z+)方指數穩定。 先證明當p=2時,定理1結論成立。 首先由隨機系統(3)的兩邊積分得 (5) 所以當t=kT+Tk時有 其中:Tk=β|Cx(kT+Tk)|, 因此 (6) 再由隨機系統 (3)兩邊從sk-1到kT積分得 (7) 即 (8) [I+MβW(Tk)]Z(sk)=eATZ(sk-1)+h(sk)。 (9) 由條件Mβ滿足-MβCB<1,可推得I+MβW(Tk)是正定矩陣,由此說明式(7)有意義。 其次,令二次李雅普諾夫函數V:Rn→R+,V(Z)=ZT(P-I)Z,其中正定矩陣P滿足(P-I)是正定的和P=(e-AT)T(P-I)(e-AT)。 因此,當t∈[sk-1,sk]有 ?E[V(x(t))]=E[V(Z(sk))]-E[V(Z(sk-1))]= E[ZT(sk)(P-I)Z(sk)]-E[ZT(sk-1)(P-I)Z(sk-1)]= E[ZT(sk)(-I-Mβ(PW(Tk)+WT(Tk)P)-M2β2WT(Tk)PW(Tk))Z(sk)]+ MβE[hT(sk)PW(Tk)Z(sk)+ZT(sk)WT(Tk)Ph(sk)]-E[hT(sk)Ph(sk)]。 (10) 記Φ(Tk,Mβ)=I+MβG1(Tk)+M2β2G2(Tk),G1(Tk)=WT(Tk)P+PW(Tk),G2(Tk)=WT(Tk)PW(Tk)。 則式(10)簡化為 ?E[V(x(t))]=-E[ZT(sk)Φ(Tk,Mβ)Z(sk)]+MβE[ZT(sk)WT(Tk)Ph(sk)+ hT(sk)PW(Tk)Z(sk)]+E[hT(sk)Ph(sk)], (11) 結合條件(1)中θMβ>0,可以得到Φ(Tk,Mβ)是正定矩陣。 接下來估計h(sk)。即證明對?μ>0,存在δ>0,當‖G‖<δ時,有 E[‖h(sk)‖2]<μE[‖Z(sk)‖2]。 因為當t∈[sk-1,sk]時,得 (12) (13) 注意到 (14) 由引理1即得 而式(14)簡化為 其中K0=I+M2β2‖B‖2‖C‖2。 再由Gronwall不等式得 E[‖x(t)‖2]≤4K0e-(‖A‖2+‖G‖2)TE[‖x(sk)‖2]。 (15) 因此 4K0K1e-(‖A‖2+‖G‖2)T‖G‖2E[‖x(sk)‖2]≤K‖G‖2e-‖G‖2TE[‖x(sk)‖2], (16) 結合條件(2)可以得到 E[‖h(sk)‖2]≤μE[‖Z(sk)‖2]。 (17) 又因為當t∈[sk-1,sk]可得 其中λm(·)和λM(·)分別為矩陣的最小特征值和最大特征值。即: (18) 注意到 V(x(0))=xT(0)(P-I)x(0)≤‖P-I‖‖x(0)‖2=‖P-I‖‖a‖2, 其中a=x(0)為初始值。 所以當t∈[0,s0]時,則E[V(s0)]≤E[V(x(0)]=‖P-I‖‖a‖2,當t∈[sk-1,sk]時,得到 (19) 注意到E[V(x(t))]≥λM(P-I)E[‖x(t)‖2],由此得到 (20) 因此,由定義1知當p=2時,隨機系統(3)在平衡點xe=0處是均方一致穩定的。 接下來證明該隨機系統(3)是p方指數穩定的。 令p=2q,q≥1,則 E[V(Z(sk))q]-E[V(Z(sk-1))q]= E[(V(Z(sk))-V(Z(sk-1)))V(Z(sk))q-1+…+V(Z(sk-1))q-1]≤ 所以 因此當t∈(sk-1,sk)時,可以得到 類似地,可以得到 因此由定義1知p為偶數時,隨機系統(3)是p方指數穩定的。類似地,可以證明,當p為奇數時,該結論也是成立的。 所以,對于?p∈Z+定理1成立。 注1 本文考慮隨機系統的p方指數穩定,且該隨機系統的解趨于平衡點的速度快于具有第一類脈沖寬度調制的隨機系統。隨機系統的解的變化情況在圖3中顯示。 推論1 假設A是赫茲穩定的,如果CB>0,且隨機系統的輸出y(t)與狀態變量x(t)線性相關。則當干擾足夠小,脈沖寬度調制參數Mβ的最大上界達到足夠大時,隨機系統(3)在平衡點xe=0處是p(p∈Z+)方指數穩定。 注2 當B是正向量,C是負向量,且Mβ上界足夠小,則隨機系統(3)將具有很強的抗干擾能力。 本文給出了一些數值例子,說明了本文的理論結果,并給出了推導結果的創新點。 因此,可以計算定理3.1中所涉及的量W(Tk),P,G1(Tk)和G2(Tk),經計算得 不妨設c=1,則Mβ∈(0,+∞)。 又因為δ<δmax, 所以 經計算得δmax=0.316。 下面應用Matlab軟件作出圖2,并用圖2來描述‖G‖的最大上界的估計值δmax與Mβ之間的關系。從圖2中可以看到δmax隨Mβ的增大而減小,并且當狀態變量遠離原點直至Tk=T時,脈沖寬度調制的輸出為+M或-M。因此,對給定的β,隨著M的增加,允許確保系統p方指數穩定的最大干擾量δmax將減小,即如果隨機系統(3)的干擾量增加(小于δmax),則可以通過減小M的值來保證該系統是p方指數穩定的,具體變化情況如圖2所示。 圖2 估計值δmax與Mβ之間的關系Fig. 2 Upper bounds for‖G‖whenMβ∈(0,+∞) 如果c=1,而Mβ∈(0,1),則計算得‖G‖∈(0,+∞),這說明具有第二類脈沖寬度調制的隨機系統具有很強的抗干擾性。 圖3 例2中的具有第二類脈沖寬度調制的隨機系統的樣本點Fig. 3 Sample response of PWM feedback system with type 2 in Example 2 圖4 例2中的具有第二類脈沖寬度調制的隨機系統的樣本點Fig. 4 Sample response of PWM feedback system with type 1 in Example 2 從圖3顯示當時間t≥3時,該系統的通解將趨于平衡點。從圖4顯示當時間t≥5時,該系統的通解將趨于平衡點。雖然這兩類隨機系統的脈沖寬度調制參數的最大上界相近,但從圖3和圖4中可觀察到具有第二類脈沖寬度調制的隨機系統的通解趨于平衡點的速度快于具有第一類脈沖寬度調制的隨機系統。 本文第一個實例考慮隨機系統(3)狀態空間為A=-1,B=1,C=c,周期為T=1,即一階微分方程模型: 根據定理1的結論,計算出當該系統達到穩定時參數Mβ的取值范圍,并用Matlab軟件作出隨機干擾系數‖G‖的最大上界的估計值δmax與Mβ之間的關系圖,并分析它們之間的變化情況。本文第二個實例考慮隨機系統(3)為二階微分方程模型: 應用Matlab軟件分別作出具有相同參數和相同初始值下的第一類脈沖寬度調制隨機系統和第二類脈沖寬度調制隨機系統的解的變化情況,有力說明第二類脈沖寬度調制隨機系統具有強抗干擾和較快趨于平衡點的優勢。2 主要結果
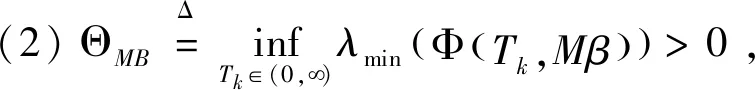
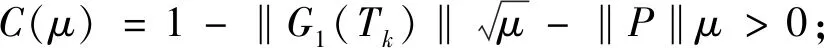
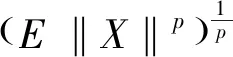
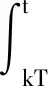
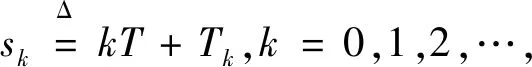
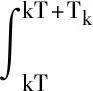
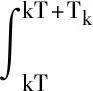
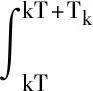
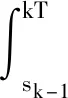
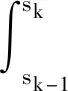
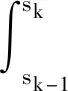
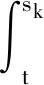
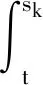
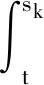
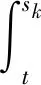
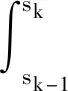
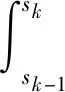
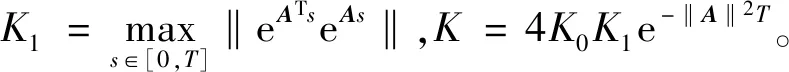
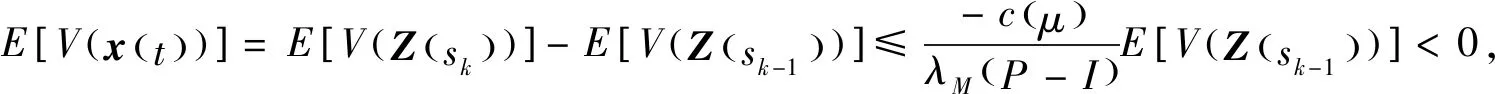


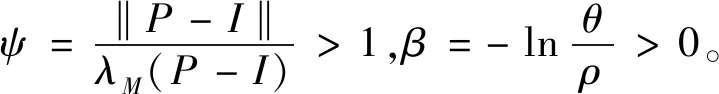
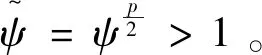
3 數值仿真