三相交流牽引供電系統牽引網阻抗計算

陳禎怡，解紹鋒，李 潔

0 引言

在電氣化鐵路牽引供電系統中，接觸導線的阻抗值是系統設計的重要參數，在計算牽引供電系統的供電能力時，計算系統阻抗值是不可缺少的環節之一。

系統阻抗求解的難點在于接觸網導線內阻抗的計算，特別是在考慮到交流電場下導線表面電流趨膚效應時的導線內阻抗計算[1，2]。對于規則圓形截面導體而言，可使用貝塞爾函數計算導線的阻抗，但是對于非規則截面導體，由于無相應的等效半徑，無法采用常規方法求解，而通常的處理方法是選取與導線等周長或等面積的圓形導體半徑作為其計算半徑[3，4]，該方法有一定的合理性，但是導體截面形狀與圓形的偏差越大，誤差越大。隨著有限元方法及相應軟件的興起與廣泛應用，非規則截面導體的電磁場計算變得容易實現，理論上可以計算任意形狀截面的導體，并通過非均勻網格的剖分獲取足夠的精度[5～7]。文獻[8]基于有限元ANSYS/Maxwell計算軟件，給出了不同型號接觸 導線交流電阻和內電感隨頻率變化曲線以及不同標稱截面積接觸導線等效半徑的計算方法。文獻[9]以P60型號鋼軌為例，闡述了ANSYS/ Maxwell建模仿真步驟，得出不同外接圓半徑下鋼軌的阻抗。文獻[10]利用有限元法和解析模型計算了鋼軌的電阻和內電感隨頻率的變化關系。文獻[9，11]從基本空間電磁理論角度出發，通過電氣參數計算新方法的研究，提出了多導體傳輸線系統回路法。

針對城市軌道交通三相供電系統中供電軌的阻抗參數求解問題，本文采用ANSYS/Maxwell軟件仿真求解非規則截面導體供電軌的阻抗參數，使用多導體回路法求解三相供電系統的系統阻抗，為三相供電系統供電能力的計算提供求解基礎。

1 城市軌道三相交流供電系統

文中針對李群湛教授團隊提出的三相交流牽引供電系統的系統阻抗進行仿真分析與計算。圖1為三相交流牽引系統示意圖，其中包括主變電所、三相電纜、牽引變壓器、三相牽引網、車載供電系統等[12]。

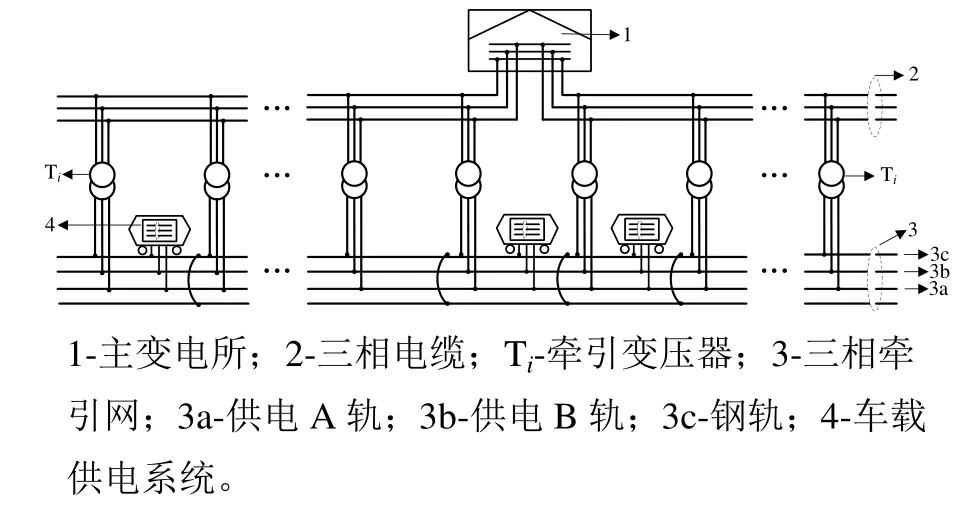
圖1 三相交流牽引供電系統示意圖

圖2為三相牽引網示意圖。三相牽引網由接觸帶和鋼軌組成，構成“兩線一地”接觸結構。接觸帶由供電A軌、供電B軌和絕緣底座及絕緣護蓋組成，鋪裝于兩鋼軌中間，供電A軌、供電B軌的安裝高度高于鋼軌的頂端[13]。

圖2 接觸帶與受電犁結構示意圖

2 鋼軌內阻抗有限元計算

由于供電軌為不規則導體，阻抗難以計算，故使用ANSYS有限元仿真軟件進行仿真計算得到供電軌的阻抗。為證明求解供電軌內阻抗仿真方法的正確性，先將該仿真方法用于P60鋼軌內阻抗計算，將仿真結果與P60鋼軌內阻抗的現有結果進行對比[8～10]。

在ANSYS/Maxwell軟件中，計算導體內阻抗的參數設置步驟：建立圖形→設置求解器→添加編輯材料屬性→設置邊界條件→添加激勵→設置劃分網格→求解設置→數據導出。

參照國家鐵道行業標準TB/T 2809—2017，在Auto CAD中繪制P60型號鋼軌截面圖。將P60鋼軌截面的CAD圖形導入ANSYS/Maxwell軟件，找到坐標原點后，在鋼軌外圍任意設置一個可以包裹住鋼軌的外邊界圓，用以設置計算時的邊界條件，外邊界圓半徑從120 mm開始設置，在鋼軌斷面上添加100 A的交流電流，仿真計算結果見表1。

取表1中10組數據的平均值，得到鋼軌內電阻為0.137 Ω/km，內電抗為0.135 Ω/km。根據文獻[14]，100 A電流情況下單條P60型號鋼軌內電阻為0.135 Ω/km、內電抗為0.135 Ω/km，仿真結果與之對比，誤差分別為1.48%、0%，可知該仿真結果與實際現有參數相差不大。鋼軌材料與供電軌中鋼部分使用的材料相同，因此該仿真方法可適用于供電軌內阻抗的參數求解。

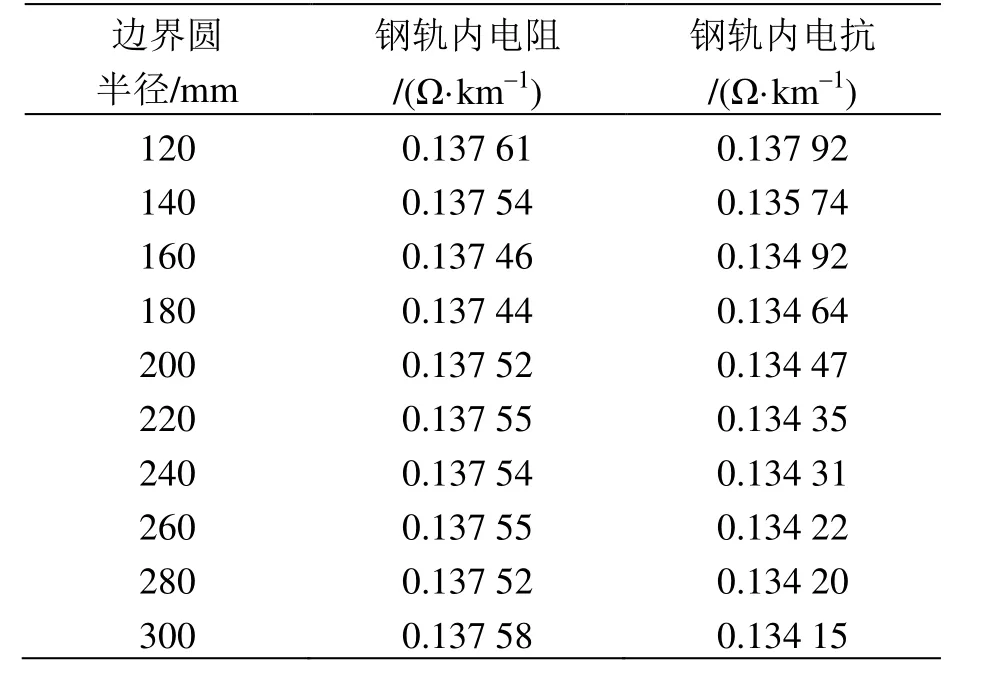
表1 不同邊界圓半徑對應的鋼軌內阻抗計算結果

3 供電軌有限元軟件計算

3.1 供電軌內阻抗仿真

由于供電軌與集電桿相接觸部分的鋼材質一面為弧面，為了簡化裝置，將弧面視為平面。設置供電軌為長63 mm、寬60 mm的矩形，頂端附有3 mm長的鋼材料，下端為導電材料鋁，在Auto CAD中繪制供電軌截面圖形如圖3所示。

圖3 供電軌截面的CAD圖形

將供電軌截面的CAD圖形導入ANSYS/ Maxwell軟件中，找到坐標原點后，在供電軌外圍任意設置一個可以包裹住供電軌的外邊界圓，用以設置計算時的邊界條件，外邊界圓半徑從50 mm開始設置，在供電軌斷面上添加100 A的交流電流。供電軌內阻抗仿真結果見表2，取該10組數據的平均值，得到供電軌內電阻為0.015 5 Ω/km，內電抗為0.025 6 Ω/km。

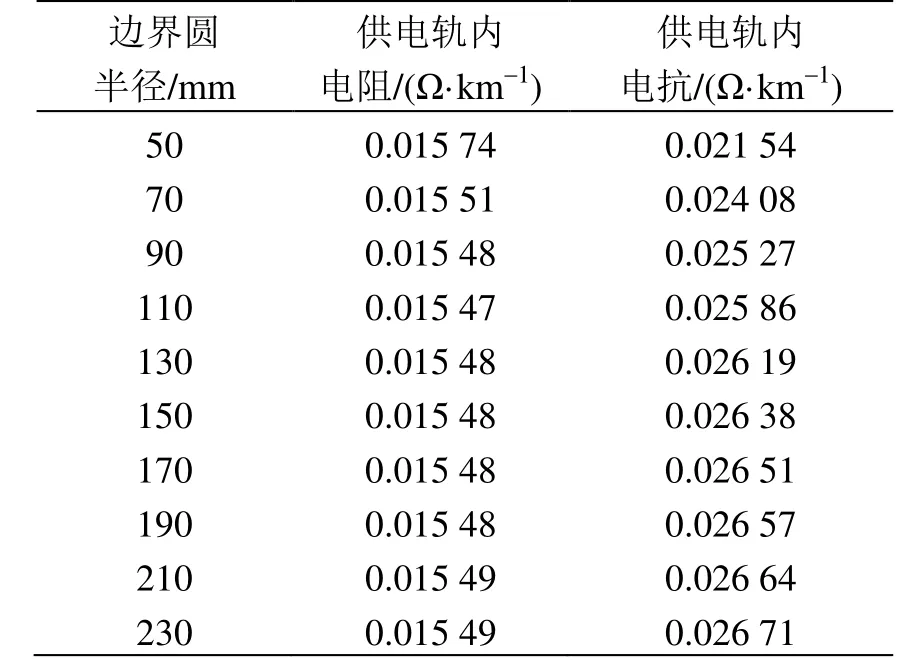
表2 不同邊界圓半徑對應的供電軌內阻抗計算結果

3.2 供電軌等效半徑計算

根據上文仿真還可得到供電軌的內電感Lin，其結果是由總電感L減去外電感Lout得到。在實際網絡計算中，外電感Lout與供電軌等效半徑Rε有關，當需要計算供電軌與其他導線的互阻抗時，等效半徑Rε是計算的一個重要參數，在有限元仿真中，可以根據外電感Lout確定等效半徑Rε。

由于內電感Lin與頻率及導體電流分布有關，頻率趨于無窮大時，電流集中在導體表面，這時內電感接近于零，因此當頻率趨于無窮大時，外電感Lout與L相等[10]。利用有限元仿真方法計算供電軌頻變參數，可以發現電感L最后趨近于一個穩定值，此時計算結果趨近于外電感Lout，取極限頻率f= 107Hz，獲得外電感Lout[15，16]。通過導線與大地的回路電感L的計算式反算等效半徑Rε，即

式中：D1p為包圍導線的圓半徑，仿真中等于外界圓半徑；μ0為真空磁導率，μ0= 4π×10-4H/km。

在f= 107Hz情況下，設置不同的外界圓半徑，得到5組不同外界圓半徑情況下的外電感及相應的等效半徑計算結果，如表3所示。由結果可知，不同外界圓半徑的情況下，供電軌等效半徑基本不變，相差較小，結果取其平均值，即R?= 36.342 mm。

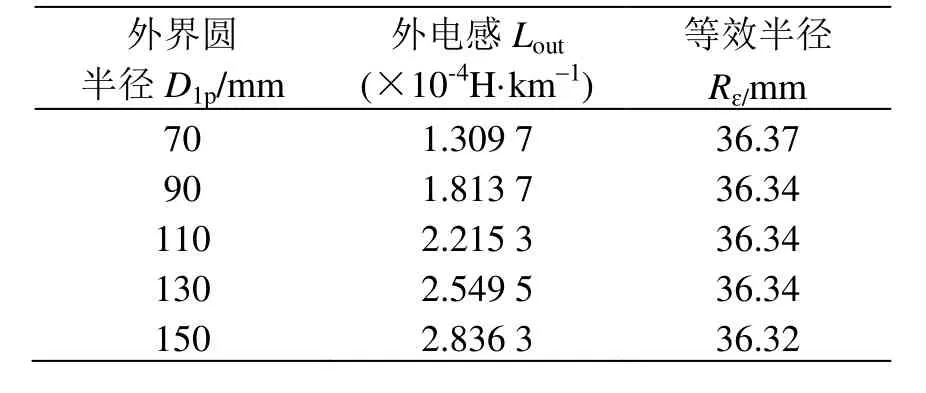
表3 不同外界圓半徑情況下的外電感及等效半徑

4 基于多導體回路系統的牽引網阻抗計算

牽引網阻抗的求解采用多導體回路法進行計算[9，11]。三相牽引網結構示意如圖4所示。

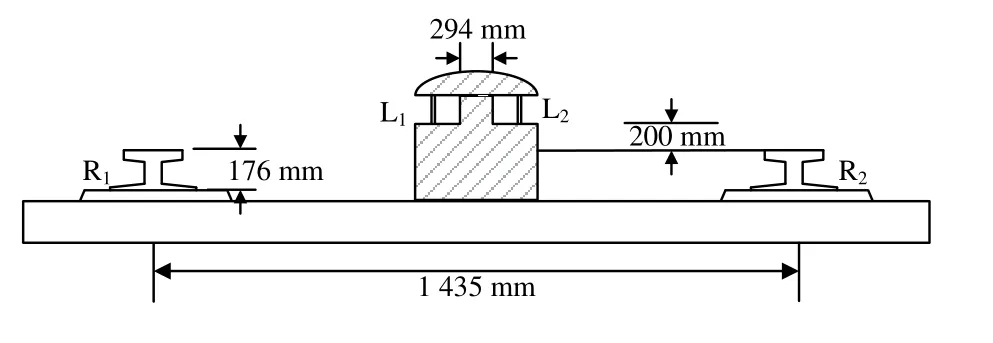
圖4 三相牽引網結構示意圖

假設供電軌L1、L2為傳輸導體，鋼軌R1、R2和大地E作為回流導體，傳輸導體與回流導體兩兩分別構成6條回路，如表4所示[11]，回路示意圖見圖5。圖中，S1為供電軌L1與鋼軌R1的距離，S2為供電軌L1與鋼軌R2的距離，S4為供電軌L2與鋼軌R1的距離，S5為供電軌L2與鋼軌R2的距離，d1為兩根供電軌之間的距離，d2為兩根鋼軌之間的距離。

表4 各回路編號

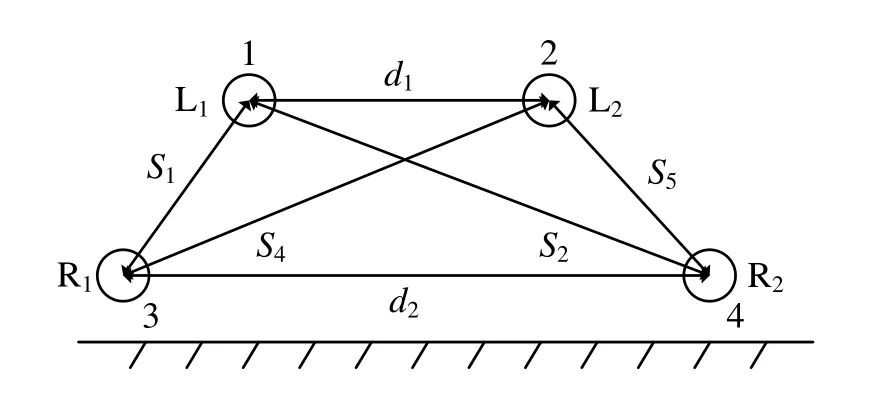
圖5 回路系統示意圖

基于表4，根據各回路電壓降與各回路磁鏈關系，當電源為正弦激勵時，可得各回路電壓降、回路阻抗和各回路電流間關系如下：

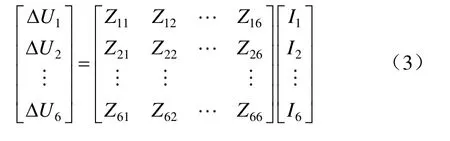
式中：Zij（i= 1, 2, … ,6；j= 1, 2, … , 6）為6條回路對應的自阻抗和兩兩間互阻抗；ΔUj為第j條回路的電壓降；Ij為通過第j條回路的電流。

由于牽引網導線長度較長且平行，各回路可視為并聯，此時有ΔU1= ΔU2= …= ΔU6。對任意回路i和回路j構成的兩回路而言（i≠j），它們的磁鏈相等，由磁鏈守恒可得

式中：lij為回路對應的自電感和兩兩間互電感。

假設I為所有傳輸導線的總電流，k1、k2、…、k6為6條回路的電流分配系數，則有

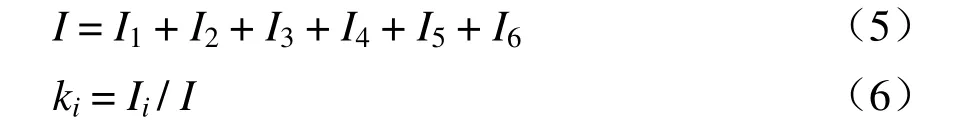
為了計算各回路電流之間的關系，先得到以下自電感與互電感：

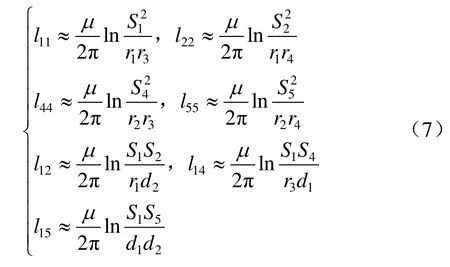
對于大地回流回路（即回路3、6），有

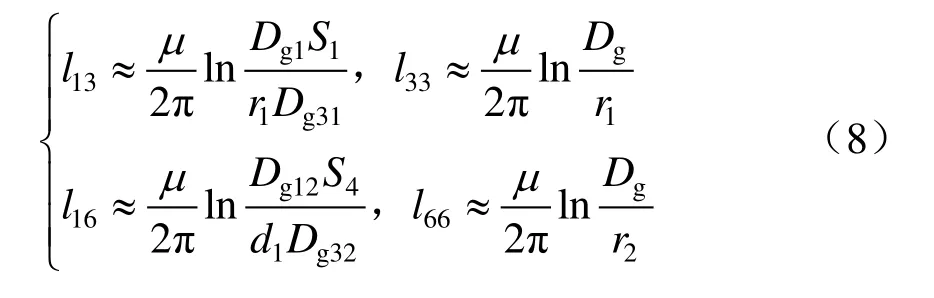
式中：ri為各導體的等效半徑；μ為回路空間磁感應系數；Dg為導線對大地的等值深度；Dg1為導體1對大地的等值深度；Dg31為導體3與導體1鏡像間的距離；Dg12為導體1與導體2鏡像間的距離；Dg32為導體3與導體2鏡像間的距離，導體的鏡像由對大地的等值深度確定。

將式（7）、式（8）代入式（4），并與式（5）、式（6）聯立，可得k1= 0.213 4，k2= 0.178 6，k3= 0.113 7，k4= 0.147 0，k5= 0.213 4，k6= 0.133 8。

將系數k1、k2、…、k6分別代入式（9），可得6條回路單位長度壓損。

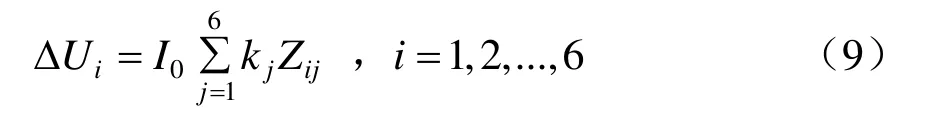
式中：ΔUi為第i條回路單位長度壓降；kj為第j條回路電流分配比例；I0為牽引網總電流。

由于牽引網各回路間可并聯等效，牽引網單位長度阻抗為牽引網單位長度電壓與牽引網總電流比值，可得各回路等效單位長度阻抗Zi為

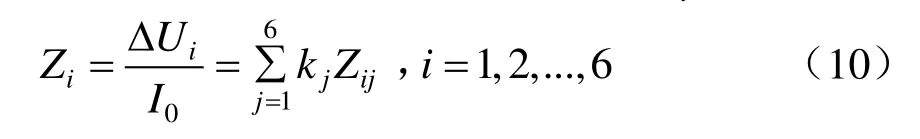
由于各回路并聯，6條回路單位長度壓降相等，故有Z1=Z2=…=Z6，故式（10）計算結果即為牽引網等效單位長度阻抗。

式（11）～式（14）為回路1相關的自阻抗及與其他導體回路間互阻抗計算式。

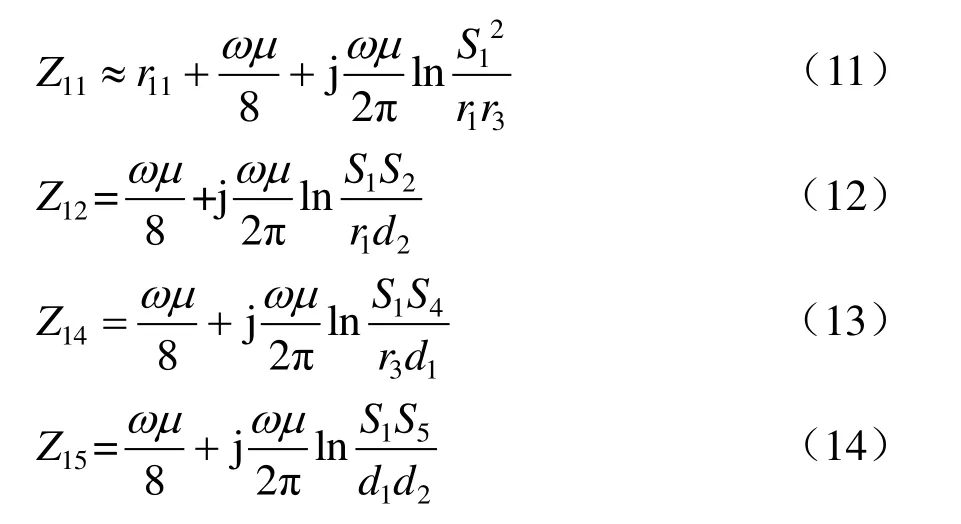
式中：ω為工頻角頻率，其值為2πf，f=50 Hz；Z11為回路1自阻抗；Z1j為回路1與回路j（j= 2，4，5）相交聯的互阻抗；r11為回路1自電阻。

對于大地回流回路與架空回流回路間的互感抗（回路1與回路3、回路6間互感抗），計算式分別為

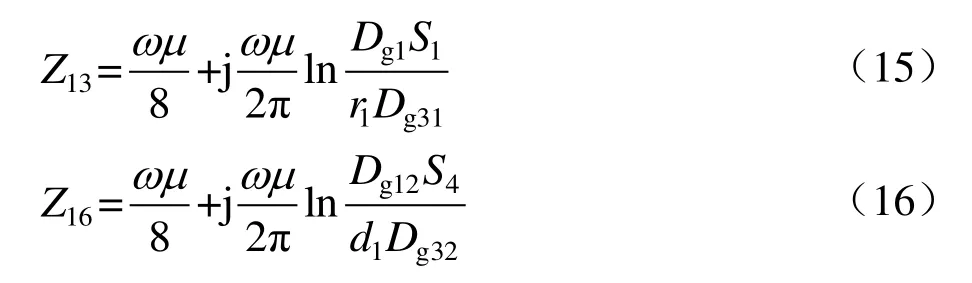
將i= 1代入式（10）中，得到等效單位長度阻抗為(0.081 1 + j0.49) Ω/km。

由于在三相交流系統中，兩根供電軌和鋼軌互為回流，傳輸導體和回流導體有6種情況，6種情況下的牽引網等效阻抗計算結果如下：

（1）兩根供電軌作為傳輸導體，鋼軌作為回流導體，等效阻抗計算結果為(0.081 1 + j0.49) Ω/km；

（2）供電軌1、鋼軌作為傳輸導體，供電軌2作為回流導體，等效阻抗計算結果為(0.054 1 + j0.154 8) Ω/km；

（3）供電軌2、鋼軌作為傳輸導體，供電軌1作為回流導體，等效阻抗計算結果為（0.054 1 + j0.154 8) Ω/km；

（4）供電軌1作為傳輸導體，供電軌2、鋼軌作為回流導體，等效阻抗計算結果為(0.056 6 + j0.225 3) Ω/km；

（5）供電軌2作為傳輸導體，供電軌1、鋼軌作為回流導體，等效阻抗計算結果為(0.056 6 + j0.225 3) Ω/km；

（6）鋼軌作為傳輸導體，兩根供電軌作為回流導體，等效阻抗計算結果為(0.078 8 + j0.211 8) Ω/km。

由于三相系統的對稱性，三相牽引網等效阻抗近似為6種情況下等效阻抗的平均值，結果為 (0.063 55 + j0.244 9) Ω/km，即三相交流牽引網的等效阻抗為(0.063 55 + j0.244 9) Ω/km。

5 結論

針對采用新型受電犁供電且供電軌為不規則導體的三相交流牽引供電系統的系統阻抗求解問題，文中采用ANSYS/Maxwell有限元軟件對供電軌及牽引網阻抗進行分析計算，得出以下結論：

（1）P60鋼軌仿真結果中內電阻和內電抗分別為0.137、0.135 Ω/km，與現有參數的誤差分別為1.48%、0%。供電軌仿真結果中內電阻和內電抗分別為0.015 5、0.025 6 Ω/km，等效半徑約為36.34 mm，該等效半徑參數在牽引網阻抗計算中尤為重要。

（2）根據仿真得到的供電軌阻抗及等效半徑對牽引網阻抗進行計算，采用多導體回路法得到三相交流牽引供電系統的牽引網阻抗為(0.063 55 + j0.244 9) Ω/km，對三相交流牽引供電系統建模及供電能力計算具有重要參考意義。